采空区群蠕变突变三维力学模型构建及稳定性精确预测
2020-01-18任红岗汪旭光谭卓英夏志远
任红岗,汪旭光,谭卓英,夏志远
(1.北京矿冶科技集团有限公司,北京,100160;2.北京科技大学土木与资源工程学院,北京,100083)
在地下矿山开采中,采用空场法开采后形成了大量采空区群,其稳定性控制是矿山生产过程中面临的关键技术难题之一。当矿柱宽度、矿柱高度、顶板荷载和岩体强度等参数处于临界范围时,稍有变化将可能引发采空区失稳和坍塌,进而诱发矿区大规模垮塌,对地质环境、矿山安全生产造成极大破坏和威胁,因此,研究采空区群的失稳机理具有重要意义[1-4]。岩石是一种能够储备高应变能的材料,地下被开采后,采空区为岩石能量的释放提供了条件。岩石所积累的应变能和势能随着开采不断变化,当这种能量平衡被打破时,将导致突发性失稳[5-7]。在开采三维空间、开采时间和应力变化的五维环境下,由顶板和矿柱构成的采空区群系统的破坏涉及蠕变和突变,是一个复杂的非线性力学问题。研究岩体力学为主的采空区稳定性问题,可以用多种多样的力学理论和方法分析,如流变力学、断裂力学、非连续介质力学、弹塑性理论、灰色理论、耗散结构理论和系统工程理论等。这些理论中突变理论应用相对较多,如谭毅等[8]基于损伤力学和突变理论,建立了条带煤柱开采形成的采空区群失稳模型;徐恒等[9]建立了顶板结构的尖点突变力学模型,计算充填体下的采空区稳定性及失稳机制。夏开宗等[10]基于非线性力学,构建了矿柱-护顶层支撑体系发生破坏的力学模型;王金安等[11-12]基于岩体流变力学理论,建立了采空区流变力学模型,揭示了采空区突变和失稳的力学机理与过程。以往研究采空区稳定性时,较多应用二维平面力学,不能直观表达三维真实情况,且多集中于研究单个或几个采空区,缺少对采空区群的整体稳定性研究,未能全面、精准反映采空区群的动态破坏过程。为此,本文在前人基础上,依据弹性力学和蠕变突变力学理论,建立矿柱顶板为系统的采空区群模型,在三维环境下,将矿柱-顶板系统等效为一系列Burger体蠕变力学模型,应用突变理论分析失稳机制,得到在不同采空区群参数下,矿柱宽度、矿柱高度、顶板荷载和岩体强度等主控因子影响特性,并总结各主控因子临界值分布规律,在矿柱蠕变作用下,可以对采空区稳定时限进行预测,为采空区群稳定性分析、识别和控制提供了量化参考,是实现矿山安全、高效、经济开采不可缺少的关键数据。
1 采空区群力学模型
1.1 双向分层条式充填采矿法
双向分层条式充填采矿法是开采中厚、层状、缓倾斜和破碎矿体的一种新的方法,图1所示为双向分层条式充填采矿示意图。由图1可见:矿块在水平方向上可划分成条带采场,纵向可划分成2层或若干层,每个采场分上、下步骤开采,上层矿体开采完之后要对顶板进行支护,矿石由铲运机经位于采场两端的上部巷道运出,随后开采下层矿体,矿石由铲运机经位于采场中间的下部巷道运出。待2层矿开采完之后,采用废石胶结充填采场并接顶。采场间开采顺序通常按照隔一采一的方式,其开采工艺可简单地概括为切顶、护顶、降底和充填4个工序。采用双向分层条式充填采矿法在第1步骤开采后,采场和矿柱在空间上呈长条状分布,形成由一系列矿柱支撑顶板的系统,在纵向上形成采场、矿柱交错布置矩形结构。
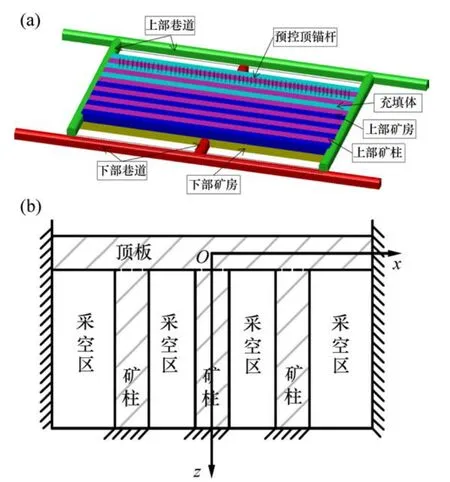
图1 双向分层条式充填采矿法示意图Fig.1 Sketch of slicing and strip filling mining method
1.2 力学模型构建
1.2.1 采场力学模型
矿房矿柱呈条形依次间隔布置,开采时,通常将若干个条形矿房矿柱组合成1个开采单元,开采后,形成由若干个矿柱支撑顶板的系统。在三维空间上,矿柱可等效为弹性体,采场顶板可等效为弹性薄板,系统受力主要考虑顶板上方的垂直应力。设采场顶板长和宽分别为2a和2b,采场高度为H,矿柱顶板力学模型体系如图2所示。
假设条件:1)采场呈规整的矩形,由若干个采场和矿柱组成1个系统,且采场矿柱分布均匀;2)采场顶板长度大于其宽度,即b>a;3)采场顶板所受荷载相对恒定;4)采空区底板足够稳定,忽略其底板的微小位移。
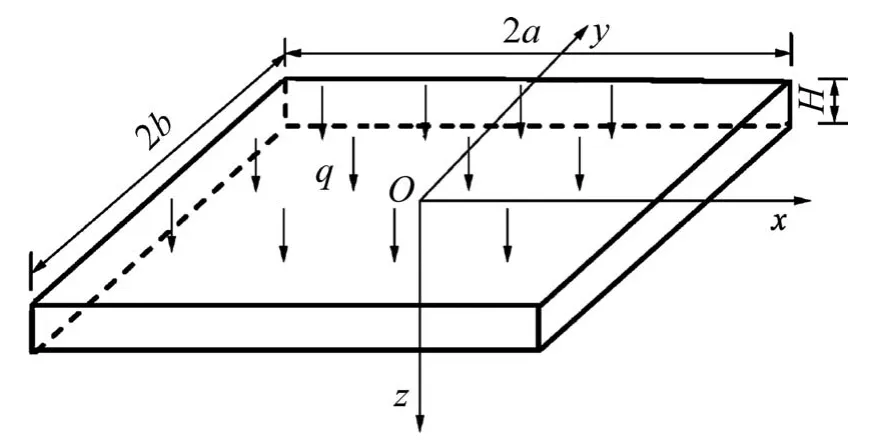
图2 顶板-矿柱力学模型体系Fig.2 Mechanical model system of roof and pillar
Burgers体蠕变模型能够描述弹性应变、衰减和稳态蠕变的力学模型,将矿柱系统等效为一系列Burgers体支撑的模型,建立顶板-矿柱弹性模型如图3所示,顶板上覆岩层的均布荷载为q0,顶板密度为ρ,抗拉强度为σT,Burgers体元件简写为B。
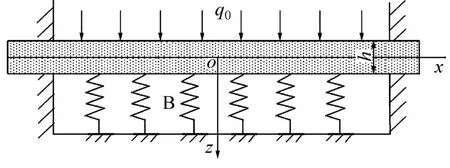
图3 顶板-矿柱弹性模型Fig.3 Elastic model of roof and pillar
顶板-矿柱系统模型的控制方程为[11]

式中:D为顶板刚度,v为泊松比;w为顶板的下沉挠度;ξ为矿柱支撑顶板的面积与顶板总面积的比率,称为面积比率;σ为矿柱应力。
1.2.2 顶板挠度算法
矿房开采后,采空区群发生破坏一般要经历3个阶段[13],每个阶段支撑顶板模型如下。
阶段I:固支边界模型。在开采初始条件下,矿柱和顶板均未发生破坏,此时可视为固支模型,顶板的挠度曲方程为[6]:

式中:w(x,y)为顶板的下沉挠度;w0为顶板中心下沉挠度;φ(x,y)为顶板下沉挠度的比例函数。
阶段Ⅱ:简支边界模型。随着矿柱承载力逐渐下降,顶板下沉位移逐渐变大,进而导致顶板边缘发生塑性变形。当顶板边缘开始发生破坏时,固支模型转化为简支模型,此时有

顶板边缘破坏条件为
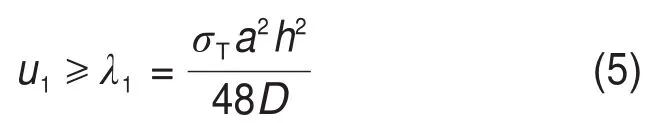
式中:u1为系统进入第I阶段后顶板中心下沉位移;h为顶板的厚度;σT为顶板抗拉强度;λ1为常数。
利用Matlab软件将式(3)和式(4)函数方程绘制成三维曲面,如图4所示。由图4可见:固支模型的顶板下沉挠度呈“尖细”状,简支模型的顶板下沉挠度呈“宽粗”状,且中心下沉挠度范围也增大。
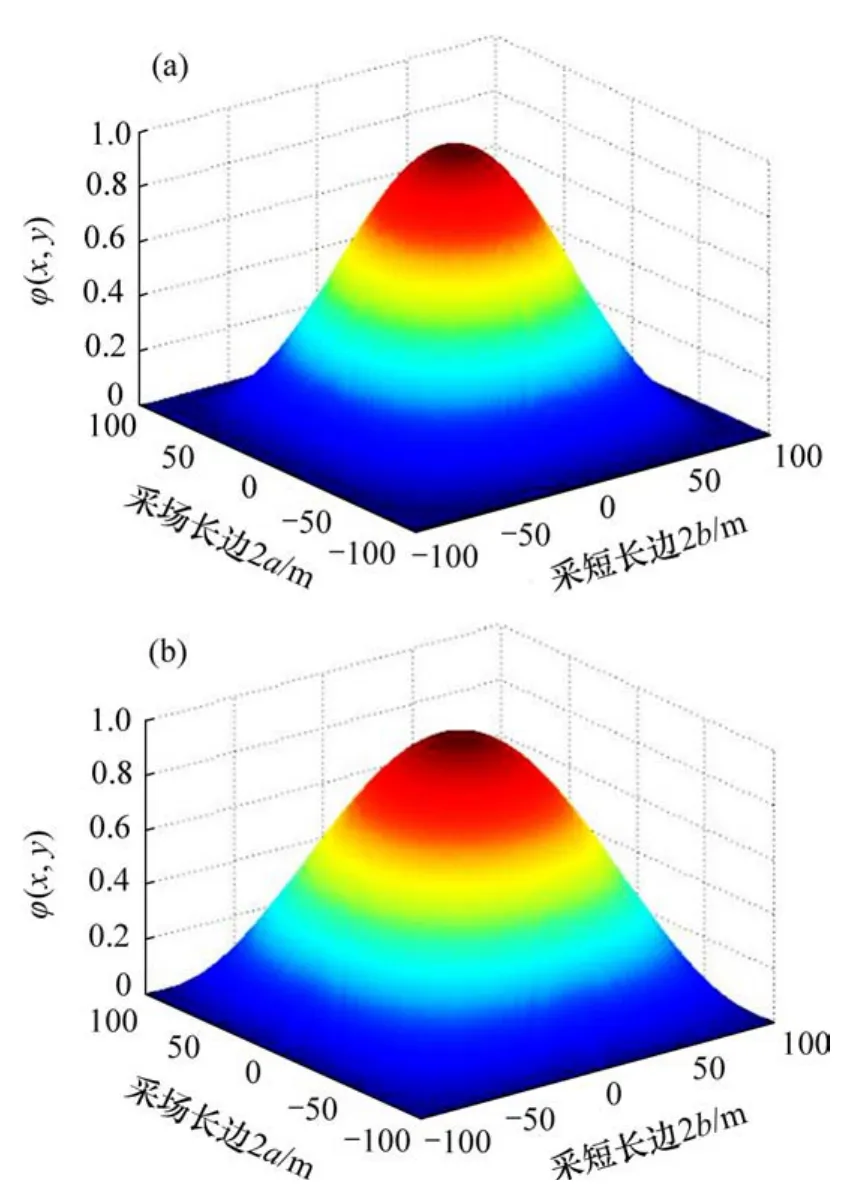
图4 顶板中心下沉挠度三维曲面Fig.4 3D surface of roof center subsidence deflection
阶段Ⅲ:自由边界模型。当顶板边缘整体破坏时,四周支撑相当于自由边,矿柱完全支撑着顶板及其上覆岩层的荷载,此时,顶板下沉挠度与其刚度无关,主要受矿柱的自身强度影响,此时,D=0,w=u,且有

顶板整体破坏时的条件为

式中:u2为第Ⅲ阶段顶板中心下沉位移;λ2为常数。
根据损伤力学理论,矿柱应力应变关系可用Weibull分布描述,其应力与应变关系如下[14]:

式中:ε为矿柱应变;ε0为曲线σ-ε峰值点纵坐标的平均数;m为试验拟合的均匀性指标。Weibull分布σ-ε峰值前的曲线与一元三次函数曲线具有较高的相似性,σ-ε峰值前曲线也可用下列表达式表示:
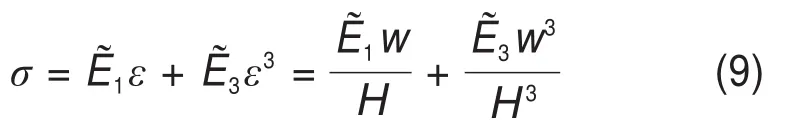
1.2.3 采场蠕变模型
矿柱变形具有随时间变化的蠕变性,采用Burgers体模型来计算,如图5所示,本构方程如下[11]:
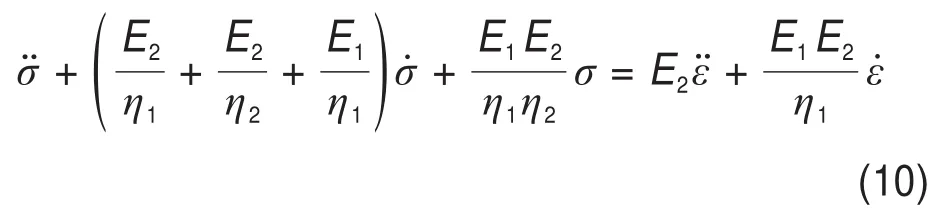
式中:E1和E2为弹性系数;η1和η2为黏性系数。
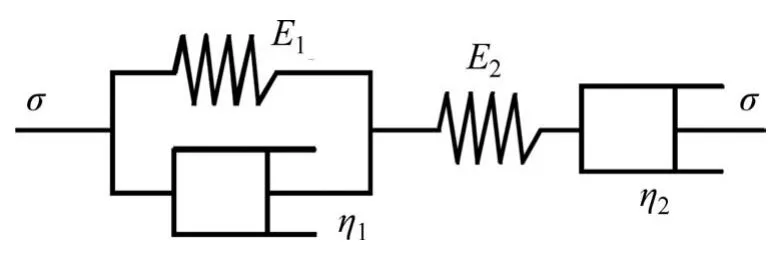
图5 矿柱Burgers物理本构模型Fig.5 Burgers physical constitutive model of pillar
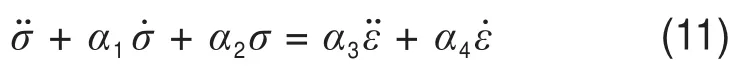
联立式(1)和式(11),消去矿柱应力σ得

1.3 挠度曲线方程
将式(1)与式(2)联立,通过伽辽金法求得
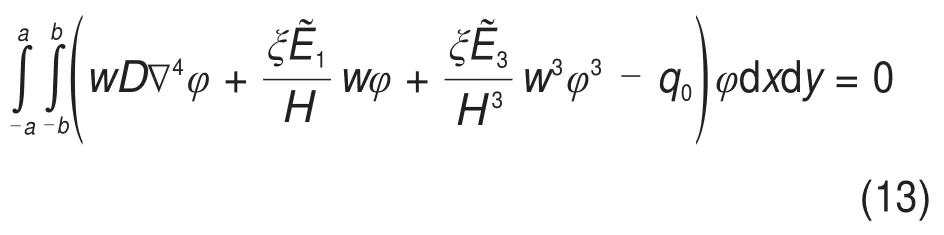
令
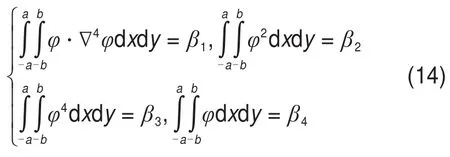
阶段I:当顶板处于固支模型时,将式(3)代入式(14)求得

阶段II:当顶板处于简支模型时,将式(4)代入式(14)求得
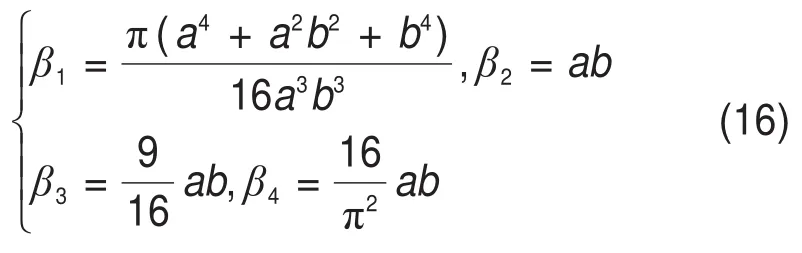
阶段Ⅲ:当顶板处于自由边模型时,将式(6)代入式(14)求得
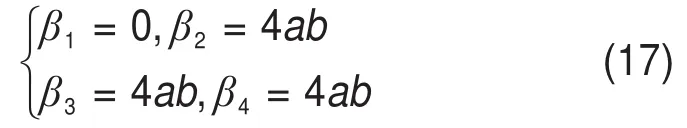
联立式(2)与式(12),采用伽辽金法求得

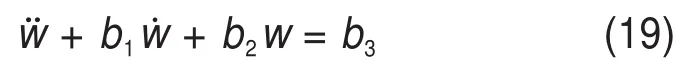
式(19)微分方程通解为
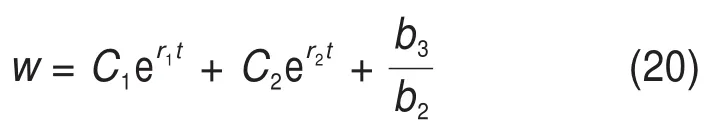
根据王金安等[13]的研究成果,矿柱在最初受压时会产生瞬时变形,阶段I中式(20)初始位移和下沉速度为

式中:σ0=w0ξE2,为矿柱初始应力。阶段II和阶段Ⅲ位移和速度的初始值分别为上一阶段末期的对应值。
2 采空区群突变及失稳机制
2.1 突变理论分析
突变理论用于研究系统从一种稳定状态向另一种稳定状态转化的规律[15-16],采空区群失稳是一个渐进的、非线性过程,突变理论是计算这种失稳过程的有效方法。对于复杂的内部系统奇点附近不连续问题,可利用突变理论构建的数学模型,找到在系统临界点的突变规律,能有效预测和判别岩体工程稳定性。尖点突变的势函数模型如下:
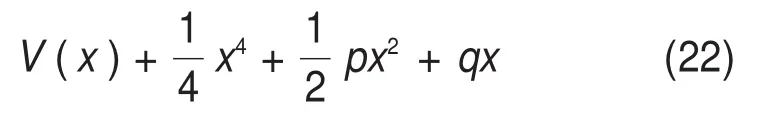
式中:V(x)为尖点突变势函数;x为状态变量;p和q为控制变量;这3个变量构成系统的相空间。
通过对势函数求导可得相空间的平衡曲面方程:

对势函数求二阶倒数得系统的奇点集方程:
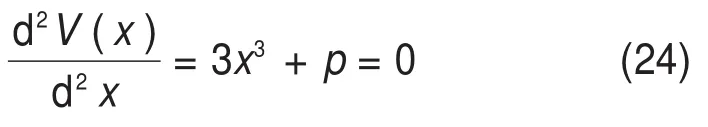
联立式(23)和(24)得分叉集方程为

式(25)中,p为非正数是方程有实数解的前提条件,这也是突变产生的必要条件。
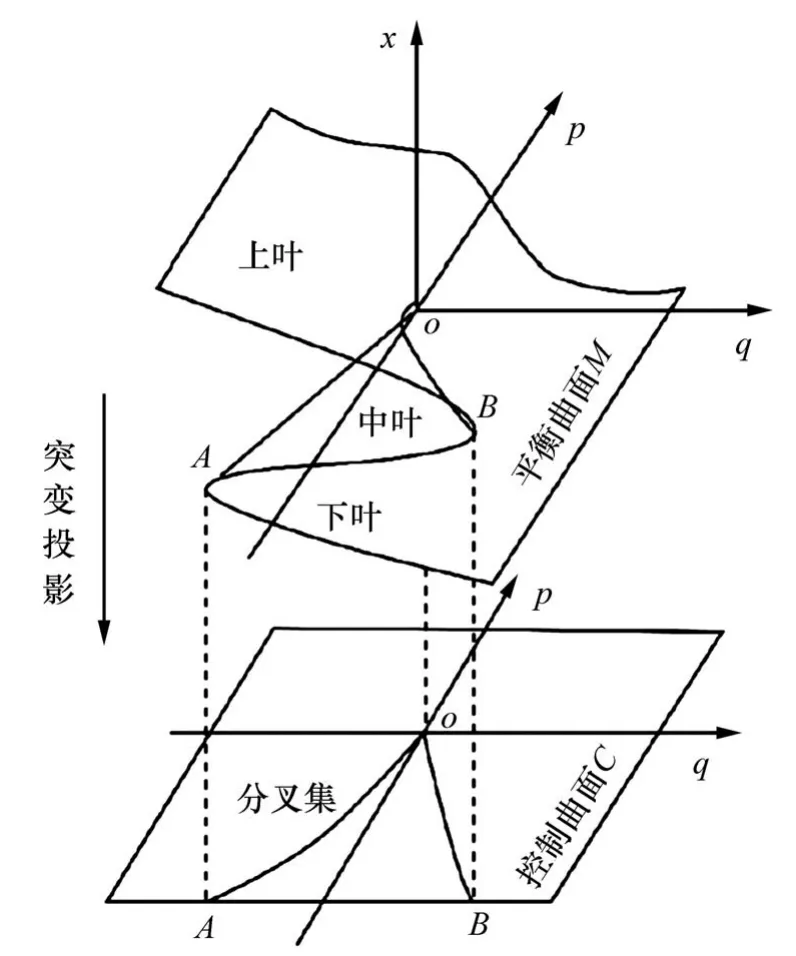
图6 尖点突变模型Fig.6 Cusp catastrophe model
图6所示为尖点突变模型的示意图。相空间的图形可以看作一个褶皱的曲面,该曲面的折叠图形上分别由上叶、中叶和下叶构成。当平衡曲面位于上叶或下叶时,系统处于发展过程的准稳定状态;当平衡曲面位于中叶时,系统处于不稳定状态,即将发生突变,进入一个新的平衡状态[17-18]。
2.2 势函数构建
从能量转化角度分析,采空区群势函数表达式为

式中:U为采空区势能;Ue和Us分别为顶板和矿柱的应变能;W为外力作用所做的功。按照薄板的弯曲理论,在固支、简支和自由边模型下,顶板应变能Ue表达式不尽相同。
阶段I:当顶板处于固支模型时,应用薄板理论的顶板应变能表达式为

利用Matlab软件解算出
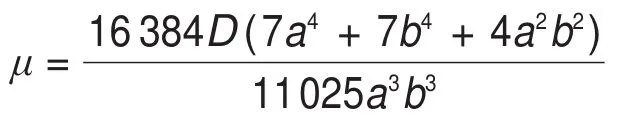
阶段Ⅱ:当顶板处于固支模型时,顶板应变能表达式为
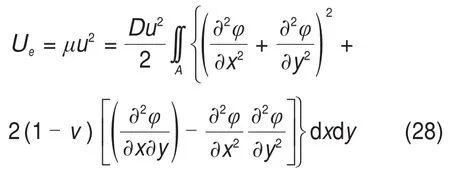
式中:u为顶板中心下沉位移;μ为顶板等效刚度。
阶段Ⅲ:当顶板处于自由边模型时,顶板应变能为零。
矿柱压缩应变能Us为
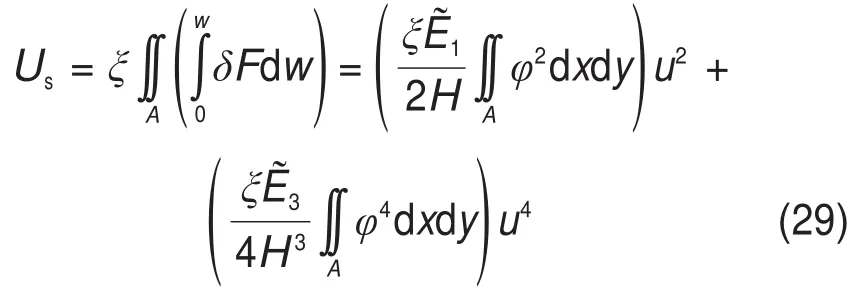
外力做的功W为
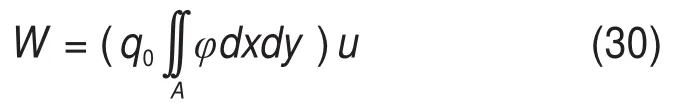
由式(22)~(25)得势函数表达式:
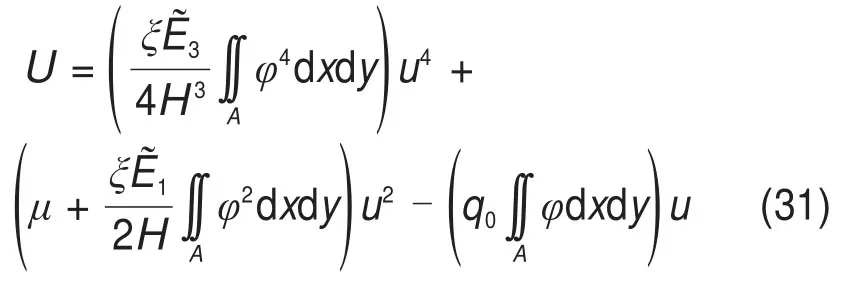
对式(31)求偏导数,得

对式(32)整理成如下格式:
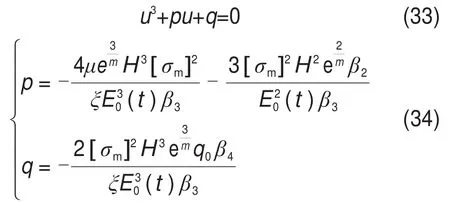
2.3 采空区群系统突变失稳分析
2.3.1 突变失稳计算
图7所示为采空区群系统突变失稳计算流程。由式(27)求出μ1,将其代入式(34)并联立式(25),可求出面积率临界值ξ1,将其代入(33)求出顶板下沉挠度u1。若u1<λ1,则突变点系统处于阶段I,否则依次计算μ2,ξ2和u2;若u2<λ2,则突变点系统处于阶段Ⅱ,否则,处于阶段Ⅲ。
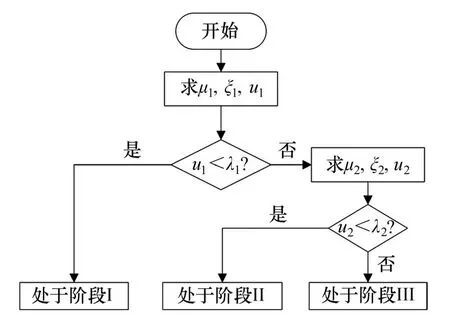
图7 采空区群系统突变失稳计算流程图Fig.7 Flow chart for calculating catastrophic instability of goaf group system
表1所示为双向分层条带式采空区岩体参数,采场长180 m,宽120 m,代入数据求得ξ1=0.471 3,u1=0.124 1 m,λ1=0.045 7 m,故u1>λ1,系统不处于阶段Ⅰ;继而求得ξ2=0.491 2,u2=0.130 6 m,λ2=0.088 6 m,故u2>λ2,系统不处于阶段Ⅱ,而处于阶段Ⅲ。
表2所示为不同采空区群系统突变失稳计算结果,分别列出在固支模型、简支模型下的顶板位移和破坏条件,表2中所列出的采空区群均会发生突变,采矿过程中要及时对采空区进行充填处理。

表1 采空区群顶板-矿柱岩体力学参数Table 1 Mechanical parameters of roof and pillar rock mass in goaf group
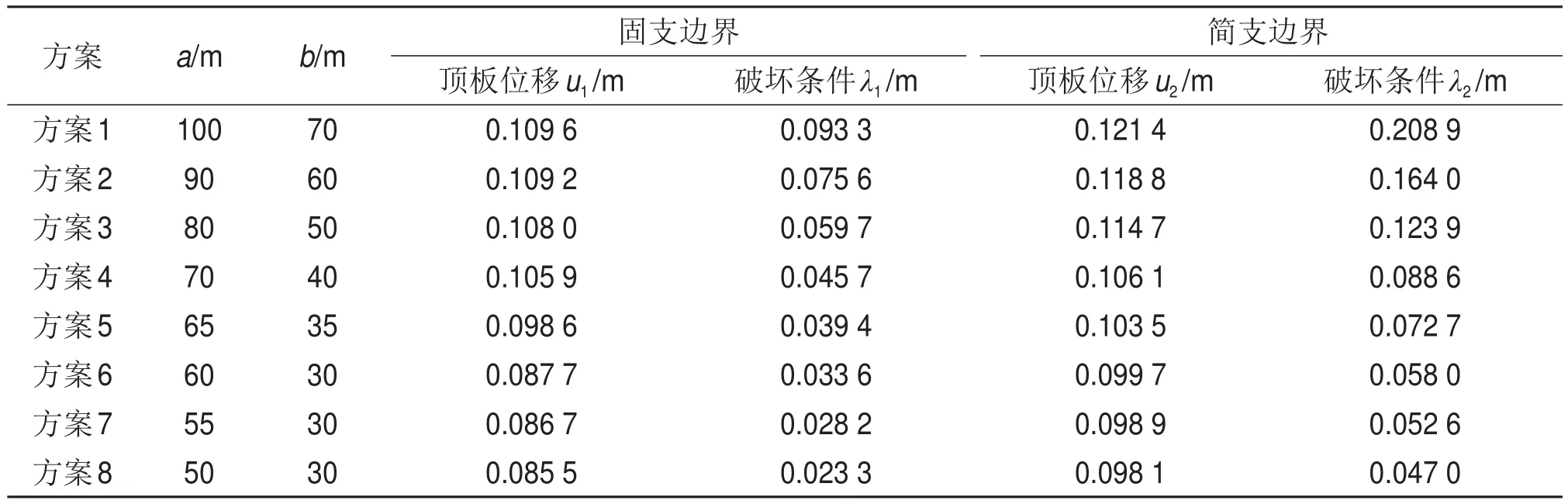
表2 不同采空区群系统突变失稳计算结果Table 2 Calculation results of catastrophic instability of different goaf groups
2.3.2 数值模拟分析
采用数值模拟研究分析[20],将3Dmine,MIDAS和FLAC3D这3种软件耦合,充分利用软件在图形处理、复杂建模和定制计算等方面优势,分别研究采场空区群在不同边界状态下的稳定性。建立的矿区及采场数值计算三维模型如图8所示。
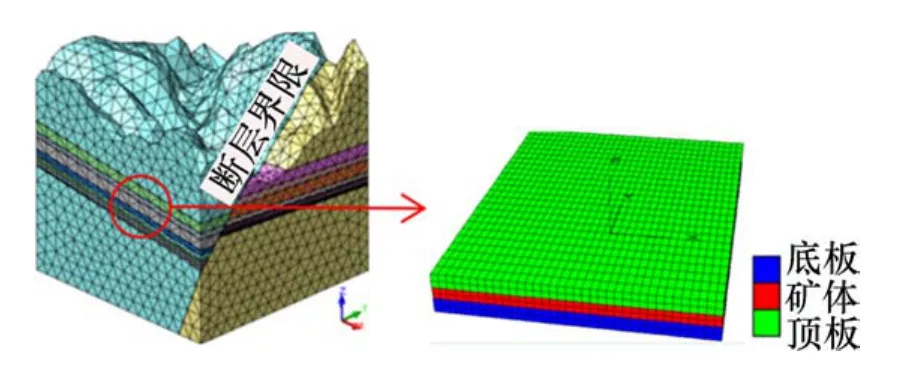
图8 矿区及采场三维数值计算模型Fig.8 3D numerical calculation model of mining area and stope
图9所示为采空区群下沉位移云图,由图9可见:采场顶板中心位移及其范围随采场参数减小而变小。图9(a)中顶板中心最大位移区域占采场顶板区域的1/2,表现出明显的不稳定性,引发顶板大面积垮塌和突变失稳;图9(c)中顶板相对较稳定;图9(b)中顶板稳定性居于图9(a)和图9(c)中顶板稳定性之间。
图10所示为从三维角度分析同一采空区群在阶段Ⅰ和阶段Ⅱ的顶板下沉位移。由图10可见:阶段Ⅰ和阶段Ⅱ采场顶板下沉中心位移分别为0.10 m和0.12 m,即简支模型下的顶板位移要大于固支模型的顶板位移,说明采场顶板边缘发生塑性变形后,顶板整体刚度减小,进而导致顶板中心下沉挠度增加,这与理论计算结果是一致的。
2.4 采空区群系统蠕变失稳分析
2.4.1 系统阶段Ⅰ破坏时间
矿柱蠕变参数按照已有研究成果选取[19],E1=8.0×105MPa,E2=5.5×104MPa,η1=1.05×104MPa·h,η2=1.98×109MPa·h。由式(21)可计算初始位移和下沉速度分别为w=0.000 6 m,w=v0=0.001 6 m/h。t=0时,代入式(20)求解C1和C2,根据这些初始值,确定微分方程系数:
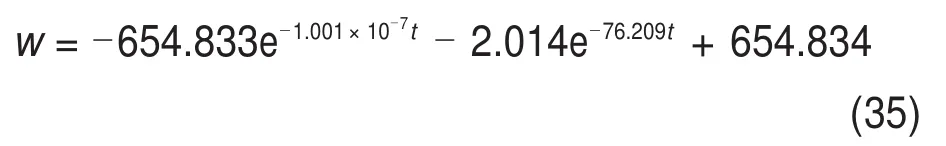
根据式(5)破坏条件,求解上述线性方程,得系统在阶段Ⅰ破坏时间为688 h。
2.4.2 系统阶段Ⅱ破坏时间
阶段Ⅱ的顶板初始位移和速度为阶段Ⅰ结束时的位移和速度,分别为w=0.045 7 m,w=6.552×10-5m/h,代入式(33)得t=0时,微分方程系数为
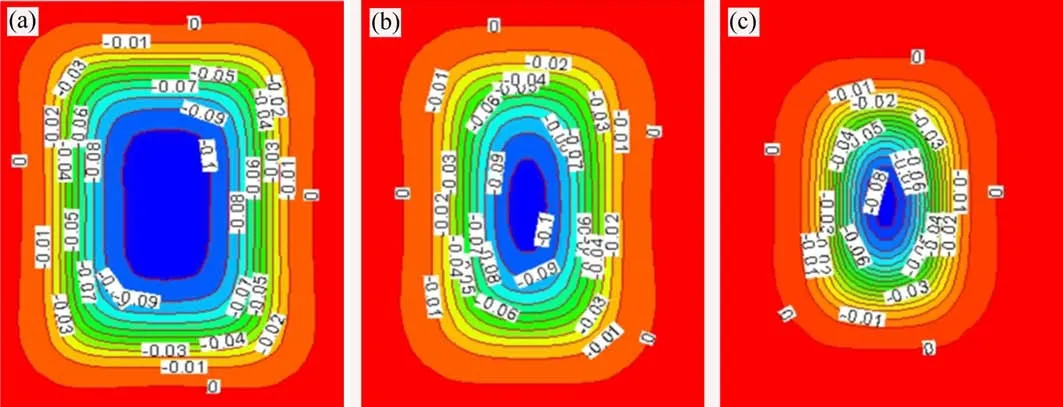
图9 采空区群顶板下沉位移Fig.9 Roof subsidence displacement of goaf group
根据式(7)破坏条件,求解上述线性方程,得系统在阶段Ⅱ破坏时间为693 h。系统在进入阶段Ⅱ之后,顶板出现破裂,虽然没有整体垮塌,顶板已经处于破裂状态,认为已失去稳定性,采空区稳定预测时间按照阶段Ⅰ和阶段Ⅱ破坏时间之和计算,因此,顶板-矿柱系统破坏时间为1 381 h,约为2月。
3 采空区群系统失稳因素分析
3.1 影响因子对顶板下沉位移影响
顶板下沉位移为采空区群系统稳定性的关键指标,从式(33)~(34)可以看出影响采空区群稳定性的主要因子有:采场参数a和b,矿柱支撑面积率ξ,均布荷载q0,矿柱峰值抗压强度σm和矿柱弹性模量E0。下面选取几组不同采场参数,分别分析各影响因子对顶板下沉位移的影响。分别将式(15)和(16)代入式(33)和(34),可得到以ξ,q0,H,σm和E0为自变量,以u为因变量的隐函数。阶段Ⅰ和Ⅱ在蠕变突变发生机制方面具有代表性、相关性和可比性,因此,分析采空区群系统失稳因素,主要针对这2个阶段进行对比。当其他自变量值一定时,绘制单个自变量对因变量u的影响曲线,如图11和图12所示。
图11(a)和图12(a)可见:对于参数确定的采场,随着ξ减小,顶板位移逐渐增大,直至曲线的拐点处(临界值)产生突变失稳;采场参数越大,保持系统稳定所需的ξ越大;系统由阶段Ⅰ至变化至阶段Ⅱ时,保持系统稳定所需ξ均变大,采场参数越小时变化越明显;在阶段Ⅱ,不同采场ξ的差值在缩小。从图11(b)和图12(b)可见:采场参数越大,能承受的q0越小。此外,阶段Ⅰ与阶段Ⅱq0变化幅度与采场大小呈反比。在图11(a)和(b)以及图12(a)和(b)中,曲线拐点处以下部分为有效研究内容,拐点处以上部分无意义,研究时不予考虑。
从图11(c)和图12(c)可见:顶板位移随矿柱峰值抗压强度σm增大而呈“L”型曲线减小,在接近σm的临界值时,顶板位移变化幅度最大;当σm超过某一特定值后,顶板位移接近恒定值。从图11(d)和图12(d)可见:顶板位移随矿柱弹性模量E0增大而呈“C”型曲线减小。
从图11和图12中可以总结出如下规律:顶板位移与矿柱支撑面积率、矿柱峰值抗压强度和矿柱弹性模量呈负相关,与均布荷载呈正相关;当顶板-矿柱系统处在固支模式时,采场参数对系统稳定性影响显著,随着采场四周出现塑性变形,采场参数对系统的稳定性差异逐渐缩小。
图13所示为不同采场矿柱稳定支撑的临界值。从图13可见:当采场参数a>90 m,b>60 m时,阶段Ⅰ与阶段Ⅱ中矿柱面积支撑率ξ趋于相近,这说明当采场参数较大时,固支模型和简支模型对采场顶板位移影响不明显。
3.2 影响因子对临界点的影响
令f=4p3+27q2,与式(34)相结合,可组成分别以ξ,q0,H,σm和E0为自变量,f(ξ),f(q0),f(σm)和f(E0)为因变量的函数,将其称之为分叉集函数。只有当f<0时,系统才发生突变;当f>0,系统没有稳定可能性。在矿山生产开采中,可通过调节影响因子参数维持系统的稳定性。
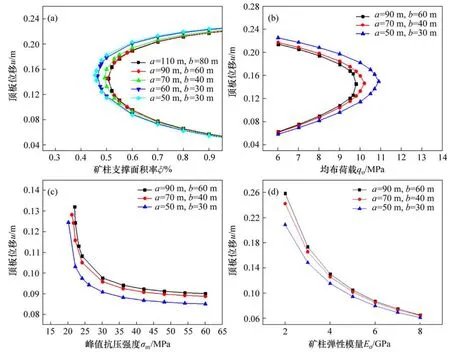
图12 阶段Ⅱ影响因子对顶板下沉位移的影响Fig.12 Influence of various factors on roof sinking displacement in stageⅡ
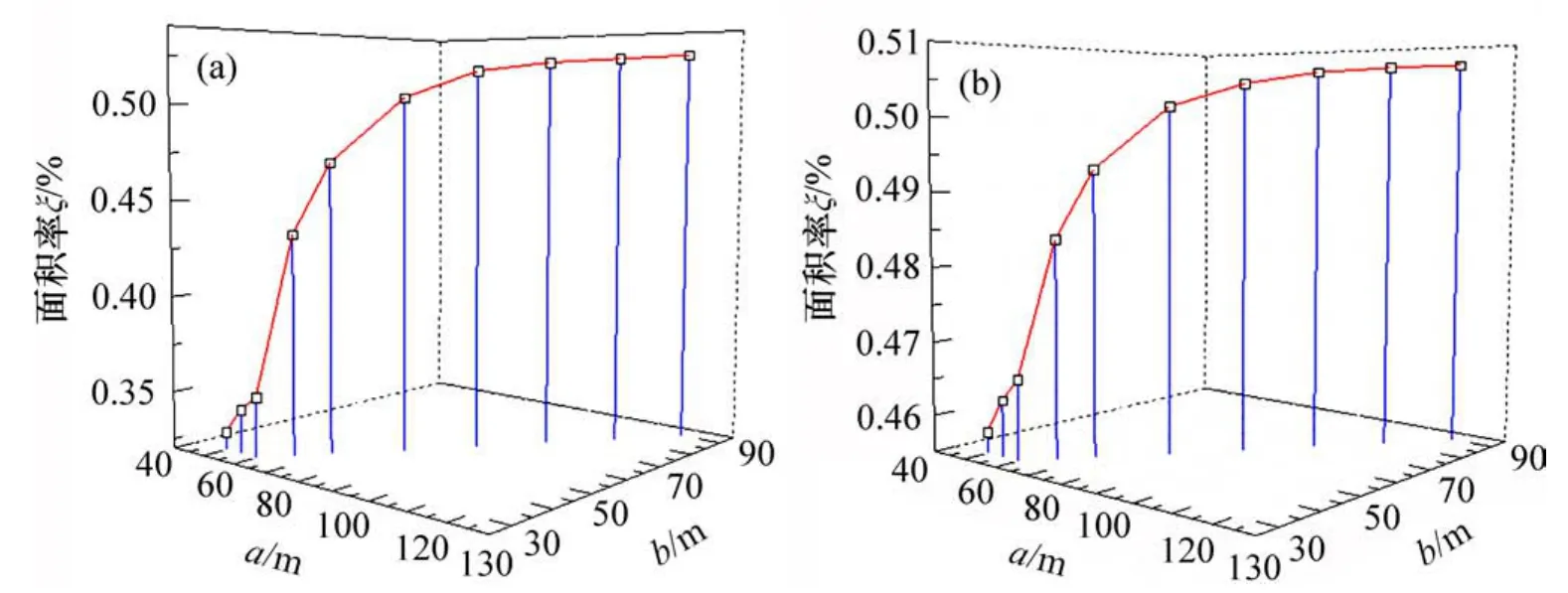
图13 不同采场矿柱稳定支撑率的临界值Fig.13 Critical value of stability support ratio of pillars in different stopes
图14所示为阶段Ⅰ影响因子对临界点的影响情况,图15所示为阶段Ⅱ影响因子对临界点的影响情况。图14(a)和图15(a)显示矿柱支撑面积率ξ对突变判别函数影响。在阶段Ⅰ与阶段Ⅱ中,不同采场结构参数下f(ξ)差距不大。图15(a)显示,当采场参数a=90 m,b=60 m时,系统在进入阶段Ⅱ中f(ξ)>0,即在阶段Ⅱ中没有稳定可能性。图14(b)和图15(b)中显示均布荷载q0对突变判别函数的影响特征,采场几何尺寸越大,q0的临界值越小。此外,阶段Ⅰ与阶段Ⅱq0的临界值变化幅度与采场几何尺寸呈反比。由图14(c)和(d)以及图15(c)和(d)可见:突变判别函数f(σm)随矿柱峰值抗压强度σm增大逐渐远离临界点,而f(E0)随矿柱弹性模量E0的增大逐渐接近恒定值。
从图14和图15总结如下规律:分叉集函数f与矿柱支撑面积率和矿柱峰值抗压强度呈负相关,与均布荷载和矿柱弹性模量呈正相关;当f<0时,f越接近零越容易发生突变。在分叉集函数f曲线中,当矿柱支撑率和峰值抗压强度大于临界值时,系统将有可能发生突变;当其小于临界值时,系统在初始状态就不够稳定,均布荷载与之相反。系统在阶段Ⅱ时,不同采场参数间均布荷载对临界点的影响趋于一致。当柱弹性模量在超过临界值后,f保持恒定,此时将不会发生突变。
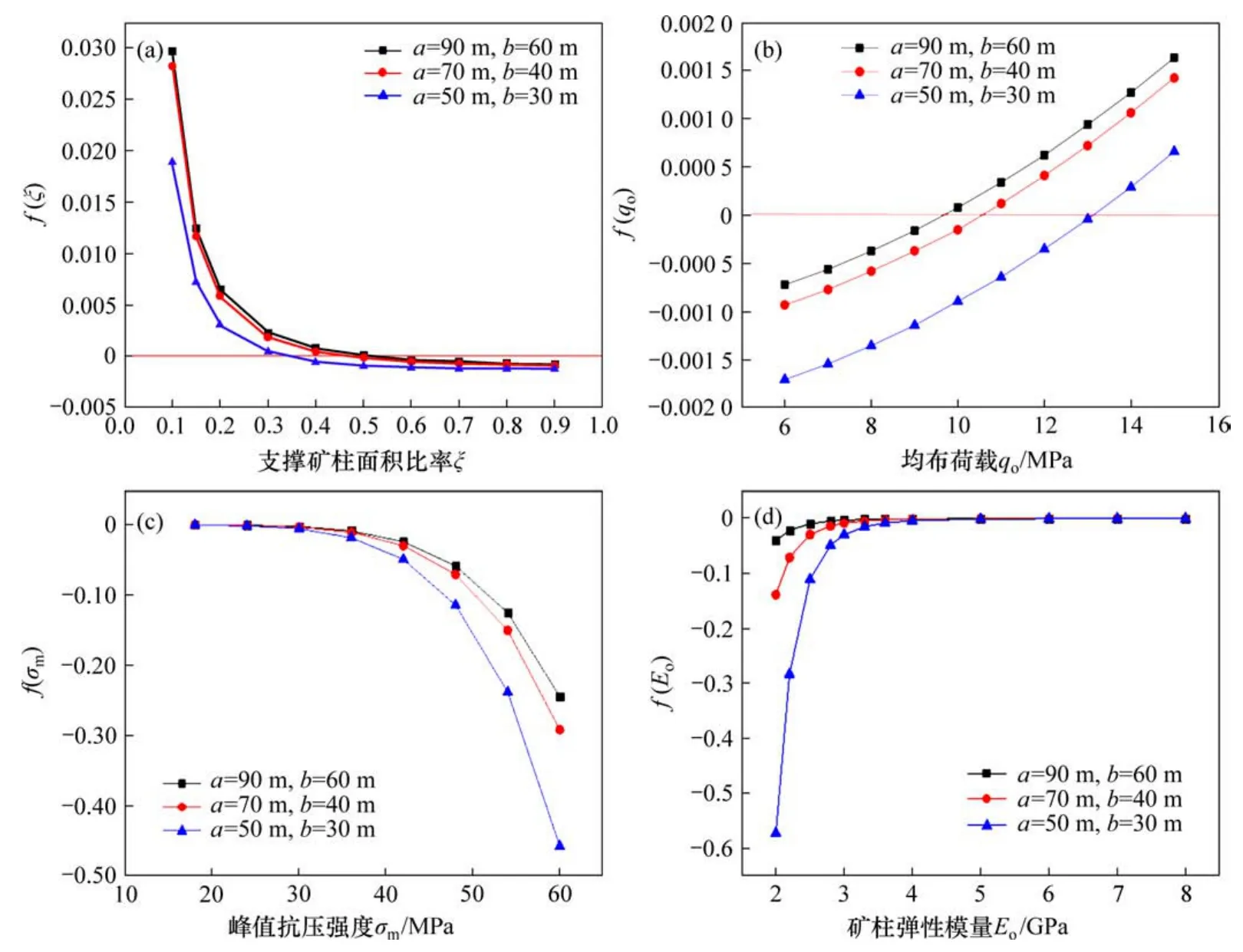
图14 阶段Ⅰ影响因子对临界点的影响Fig.14 Influence of various factors on critical points in stageⅠ
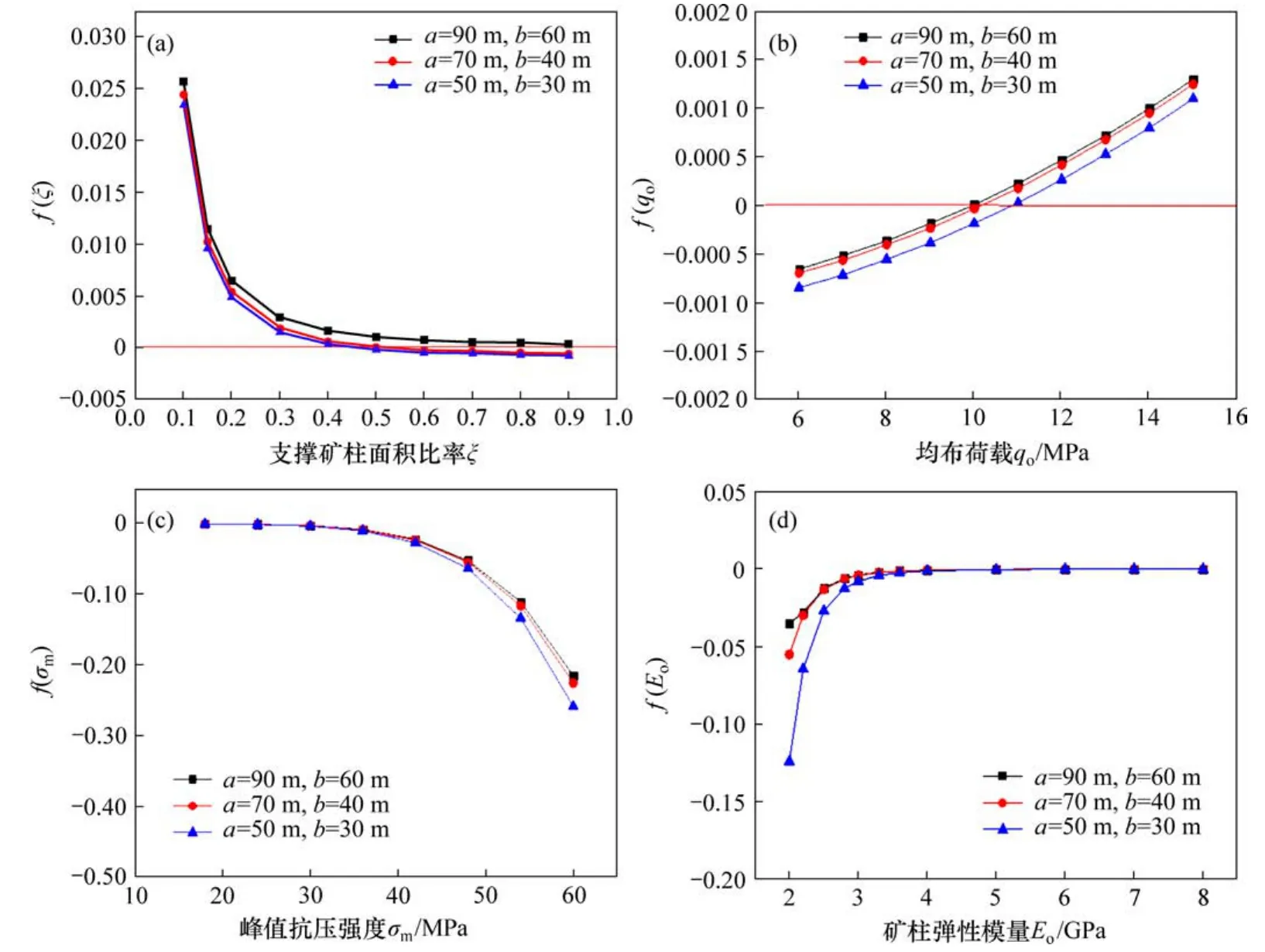
图15 阶段Ⅱ影响因子对临界点的影响Fig.15 Influence of various factors on critical points in stageⅡ
4 结论
1)将采空区势函数与尖点突变理论相结合,通过实例计算和数值模拟分析,得出多种采场参数在不同支撑边界模式下的变形特性和力学响应,从而判别出采空区群突变失稳状态,计算出采空区失稳定时间,为优化采场参数、寻找最佳充填方案、稳定性控制和安全隐患管理等方面提供依据。
2)顶板位移与矿柱支撑面积率、矿柱峰值抗压强度和矿柱弹性模量呈负相关,与均布荷载呈正相关;分叉集函数f与矿柱支撑面积率、矿柱峰值抗压强度呈负相关。与均布荷载和矿柱弹性模量呈正相关,通过调控影响因子参数,可以改变采空区的稳定状态。
3)当顶板-矿柱系统处在固支模式时,采场参数对系统稳定性影响最显著;随着采场四周出现塑性变形,不同采场参数对系统的稳定性差异在逐渐缩小;当采场参数较大时,固支模型和简支模型对系统稳定性影响差距不明显。
