地基干涉合成孔径雷达图像非线性大气相位补偿方法

胡 程 邓云开 田卫明 曾 涛

①(北京理工大学信息与电子学院雷达技术研究所 北京 100081)

②(北京理工大学卫星导航电子信息技术教育部重点实验室 北京 100081)

1 引言

作为一种高精度的形变测量仪器，地基干涉合成孔径雷达(Ground-Based Interferometric Synthetic Aperture Radar,GB-InSAR)已经在形变监测领域得到了广泛的应用[1]。GB-InSAR通常是基于差分干涉测量技术，通过对同一位置、不同时刻获取的两幅SAR图像进行差分干涉处理，基于相位信息来实现形变测量，其一般工作在X或者Ku波段，形变测量精度可以达到毫米或者亚毫米量级。GB-InSAR测量误差的主要来源是大气相位，由于不同时刻气象条件的不同，电磁波在大气中传播的速度会发生改变，从而导致大气延时误差[2]。

为实现大气相位的补偿，国内外学者主要提出了3种解决方法。第1种的补偿方法是在观测场景内建立气象站，基于大气折射率模型，利用气象数据(温度、湿度、大气压)来对大气相位进行定量估计[3]；第2种是在场景中人共布设或者选择出一些高度稳定的特征点，采用空间插值的方法实现对整幅图像的大气相位的补偿[4,5]；第3种则是基于永久散射体(Permanent Scatterer,PS)技术，根据大气相位的空间分布特征，建立描述大气相位的方程，估计大气相位参数，实现大气相位的补偿[6]。

在基于PS技术进行大气相位补偿时，首先需要选择出未处在形变区域的PS点，然后对大气相位进行合理的建模，并建立线性方程组，实现对大气参数的粗估计，此后剔除与模型偏差较大的PS点，逐步迭代实现大气参数的准确估计。该方法不需要气象参数及布设特征点，可以基于大量的PS点进行大气参数的估计，估计精度较高。一般情况下，大气在空间上均匀变化，可以将大气相位建模为随斜距线性变化的分量[7]。在地形陡峭的山区，大气在空间上非均匀变化，可以采用兼顾斜距和高程的多参数模型[8]。

基于PS技术的大气相位补偿方法，已经在GB-InSAR领域得到了广泛的应用，但还存在一些典型的问题。首先，该方法要求采用场景中的非形变PS点建立观测方程组；其次，气象条件一直在随时间改变，大气相位的时变性很强，在较差天气条件(降雨、降雪、强风等)下，大气在空间上非均匀变化，导致大气相位可能表现出复杂的空变性，无法建立合理的多参数模型来模拟大气相位。因此，常规的基于PS技术的补偿方法，在应用于时序GB-InSAR图像处理时，还存在较大的改进空间。

针对上述问题，本文借鉴在场景中布设若干个稳定的地面控制点，通过空间维插值估计大气相位的思想。首先采用常规补偿方案对所有的干涉相位图进行大气相位补偿，并分析PS点的相位序列的标准差，设定门限选择出稳定PS点；然后基于K均值聚类算法 (K-means clustering algorithm,K-means)将稳定PS点划分出一定数量的子区域，将每一个子区域的中心点设定为控制点，采用反距离加权插值算法估计所有PS点的大气相位，从而实现非线性大气相位的补偿。

本文详细介绍了补偿方法的实现流程，主要分为稳定PS点选择和空间维插值补偿两部分，然后分别采用改进方法和常规方法对460幅地基多输入多输出 (Multiple-Input Multiple-Output,MIMO)雷达图像进行了分析，对比验证了本文方法的有效性。

2 补偿方法

2.1 稳定PS点选择

在利用像素点的相位信息进行形变测量时，差分干涉相位的质量直接影响到形变测量的精度。因此，GB-InSAR差分干涉处理时，通常需要选择出一些高质量的像素点，即PS点，来进行形变分析。在GB-InSAR领域，广泛采用幅度离差法来进行PS点的选择，一个像素点的时序幅度序列的标准差与均值之比，即为幅度离差指数。通过设置合理的幅度离差门限，即可以实现PS点的选择[9]。

一个PS点的差分干涉相位 Δφ可以建模为

其中，φdefo为形变相位分量；φatm为两幅图像获取期间，由大气条件改变所导致的大气相位分量；φnoi为噪声相位分量；2kπ为相位模糊度，k为整数。由于相位周期性的影响，Δφ处在-π～π的范围内[10]。在进行大气相位补偿前，要对干涉相位图进行相位解缠，可以采用非均匀网格下的最小费用流算法，下文中采用 Δφ指代解缠相位。

大气相位φatm可以建模为

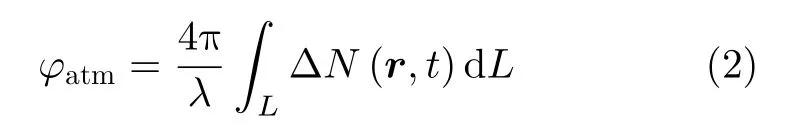
其中，λ为信号的波长，ΔN表示折射率的变化，其随着空间r和时间t发生变化，L表示信号的传输路径。一般情况下，大气的空间同质性很好，可以假设ΔN在空间r上不发生变化，在时间t上随机变化，因此可以将φatm建模为随斜距线性变化的分量

其中，β0为常数分量，β1表示与斜距相关的线性系数，R表示雷达与目标点之间的距离。基于PS技术进行大气相位补偿时，首先建立线性方程组

ΔΦ为n个PS点的解缠相位Δφ1,Δφ2,···,Δφn构成的n×1维向量，X为常数1与n个PS点的斜距R1,R2,···,Rn构成的n×2维矩阵，β为待估计的2×1维向量，ε为n×1维的随机误差向量，ε1,ε2,···,εn为各PS点的模型误差相位分量。采用最小二乘法对β进行估计，可以得到

其中，T表示矩阵的转置。大气相位的估计分量为

ΔΦ和ΔΦAPS之间的差值即为补偿后相位。首先基于所有的PS点对β进行估计，然后为提高估计的精度，剔除一些不可靠PS点。不满足式(7)准则的PS点即为不可靠PS点，ΔTatm的取值在0.1～0.2 rad范围内。剔除不可靠PS点后，基于剩余的PS点对大气相位参数进行二次估计[11]

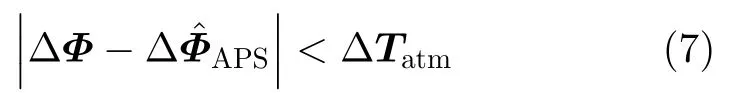
除了最基本的线性斜距模型外，常用的参数模型还包括高阶斜距模型、斜距-方位角模型、斜距-高程模型等，如式(8)-式(10)。其中β0,β1和β2是各模型中待估计的未知参数，R,θ和h分别代表目标点的斜距、方位角和高程。对线性方程组式(4)修正后，即可以进行大气相位补偿

基于PS技术的补偿方法，其有效补偿的条件，首先是要求所采用的参数模型可以准确模拟大气相位，其次是迭代估计参数时，可以有效剔除不可靠PS点。采用上述方法对一幅干涉相位图进行大气相位补偿后，一个PS点的补偿后相位ΔφAPC可以表示为

2.2 空间维插值补偿

2.2.1 子区域划分

在选择出稳定PS点后，对于每一幅干涉相位图，分别进行大气相位补偿。由于稳定PS点的相位分量中包含噪声相位和大气相位，考虑到噪声相位在干涉相位图上随机变化，不具备空间相关性，而大气相位虽然会在整幅图像范围内发生变化，但在较小的距离范围内可以视为一个常数。因此如果对空间上较小距离范围内的所有PS点进行相位平均，则噪声相位可以得到很好的滤除。由于稳定PS点是非均匀的分布在整幅图像范围内，可以基于K-means算法对稳定PS点进行簇划分，将每一个簇定义为一个子区域。每一个簇的中心点作为控制点，并对该簇内的所有PS点进行相位平均，作为当前控制点的相位。

K-means算法的实现原理是对于给定的样本集x，按照样本之间的距离大小，将样本集划分为K个簇，让各个簇内的点的距离尽可能的小，而让各个簇之间的点的距离尽可能的大[12]。假设将样本集x划分为K个簇(C1,C2,···,CK)，各簇间的平方误差和E可以表示为

其中，∥·∥表示2阶范数，即向量的模。µi是簇Ci的均值向量，可以表示为

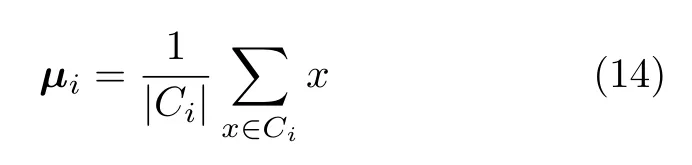
其中，|·|表示1阶范数，即簇中点的数量。

经过K-means划分后可以得到K个子区域，将每一个子区域中心点定义为控制点CPKM，其相位为该子区域内所有PS点的相位均值。

2.2.2 大气相位估计

基于这K个控制点CPKM的平均相位，进行空间维插值来估计所有PS点的大气相位，可以采用反距离加权插值算法。反距离加权插值算法是利用已知点与待插点之间的距离来定义加权因子，然后加权计算待插点的相位，距离越近加权比重越大。其计算公式为

其中，Z(x,y)为插值结果，(x,y)为待插点的空间坐标，Zi为第i(i=1,2,···,n)个参考点的数值，|di|表示待插点与第i个参考点之间的空间距离，µ表示加权因子的幂指数，一般取为2[13]。

将这些控制点视为一组离散点，可以基于Delaunay三角剖分法则来构建一个三角形网络。对于该网络内的任意一个三角形，其由3个控制点作为顶点，且外接圆中不包含其他控制点。在基于反距离加权插值算法来估计所有PS点的大气相位时，如果一个PS点处在某一个三角形内部，则以该三角形的3个控制点作为参考点，基于式(15)估计当前PS点的大气相位。如果一个PS点处在所有三角形的外部，则选择最近的3个控制点，同样基于式(15)来估计大气相位。由于每一个控制点的相位，均是通过对一个子区域内的所有PS点进行相位平均获得，则上述方法可以视为采用了大量的PS点作为参考点，空间维插值精度可以得到保证。

3 实验信息

本实验选定的区域为一露天开采矿坑(E118°36′23′′,N40°06′44′′)，其位于河北省迁安市马兰庄镇。图1(a)所示为场景照片，其中红色椭圆所示为场景的形变区域。图1(b)所示为场景卫星图，矿坑正上方为椭圆形，其长轴约1050 m，短轴约680 m，其中黄色矩形代表雷达的布放位置，雷达的观测视角范围为 60°。矿坑边坡为典型岩质边坡，基本无植被覆盖，最大开采深度约400 m，边坡倾角为38°～47°[14,15]。

实验中采用一部MIMO雷达对该矿坑进行了监测，连续获取了460幅雷达图像，时间从2018年10月26日17:30～2018年10月27日11:30。该MIMO雷达采用16个发射天线构成两个密集子阵列，16个接收天线构成一个稀疏子阵列，如图2所示。其工作在Ku波段，波长为λ=1.86 cm，等效合成孔径长度为1.138 m，角分辨率为0.466°[16]。

图3(a)所示为该露天矿坑在极坐标系下的成像结果，边坡区域内像素点的幅值主要分布在-30～0 dB的范围内。基于幅度离差法进行PS点的选择，设置幅度离差门限0.15，幅度门限-25 dB，可筛选出61764个PS点，如图3(b)所示。可以看出，坡体上大部分像素点的幅度稳定性很高，仅中间的道路上由于雷达观测视角的原因，未能有效选择出PS点。

图1 场景信息Fig.1 Scene information

图2 MIMO雷达系统照片Fig.2 Photo of the MIMO radar system

以第1幅图像为主图像，最后一幅图像为辅图像，获取差分干涉相位图，如图4(a)所示，将该相位图反投到3维地形图上，如图4(b)所示。借助于3维地形，可以更加准确地确定形变区域的发生位置。图4(c)所示为PS点的干涉相位图，显然大部分PS点的相位在0 rad左右，而红色椭圆标识出的一块区域，其干涉相位与其他区域的明显不同，该区域为发生了较大形变的形变区域。图4(d)所示为PS点的干涉相位随其斜距变化的分布图，如果将大气相位建模为随斜距线性变化的相位分量，其中红色实线所示为线性大气相位估计结果，显然存在很大的误差。因此，对较长时间基线的干涉相位图进行大气相位补偿时，如果不能合理的剔除形变PS点，将会严重影响到对大气参数的估计。在处理时序GB-InSAR图像时，为提高大气相位补偿的准确度，进行差分干涉的两幅雷达图像之间的时间基线不宜过大。

图3 MIMO雷达图像与PS图Fig.3 MIMO radar image and PS map

图4 长时间基线干涉相位图Fig.4 Interferometric phase map with long temporal baseline

4 实验结果

分析这460幅时序MIMO雷达图像时，采用相邻的两幅图像构成一个干涉图像对，则可以获取459幅干涉相位图。每一幅干涉相位图的时间基线仅为2～3 min，通常在这么短的时间内，大气条件的变化很小，相应的大气相位误差分量也很小。图5(a)和图5(b)所示为干涉相位图A和其相位散点图，所有PS点的干涉相位均在0 rad左右。在采用线性斜距模型补偿大气相位时，最大的补偿分量不超过0.05 rad。但在部分时间段，大气在空间上不再是均匀变化，导致大气相位呈现出非线性变化。图5(c)和图5(d)所示为干涉相位图B和其相位散点图，显然PS点的干涉相位变化比较复杂，采用线性斜距模型补偿大气相位时，最大会带来约0.5 rad的补偿误差，相应的形变测量误差约为0.74 mm，会严重影响到MIMO雷达的形变测量精度。即使是采用其他模型对相位图B进行分析，依然无法有效的补偿大气相位。

对459幅干涉相位图进行相位解缠，并采用线性斜距模型进行大气相位补偿，然后计算每一个PS点的补偿后相位序列的标准差。图6(a)所示为所有PS点的相位标准差图，显然形变PS点的标准差很大，设置0.3 rad的标准差门限，筛选出4341个PS点。这些PS点的分布情况图如图6(b)所示，除红色椭圆形变区域内的形变PS点外，还有少量的形变区域外的噪声PS点也被选择，如紫色椭圆所标识出的部分点。

经过相位标准差筛选后，得到57423个稳定PS点，设定每个子区域中的PS点平均数量为200个，则可以划分出287个子区域。以图5(c)所示的干涉相位图B为例来说明本文所提方法，图7(a)中红色方形点标识出了每一个子区域中心，即287个控制点，以干涉相位图B作为背景，图7(b)为局部放大图，其中每一个黑色多边形，代表各个子区域中PS点的最小外接多边形。之后对于各个子区域中的PS点进行相位平均，获取控制点的平均相位，采用反距离加权法估计所有PS点的大气相位，如图7(c)所示，可以很直观地看出，估计图中PS点的相位随其斜距呈现出非线性变化，和图5(c)高度相似。图7(d)所示则为补偿结果，所有PS点的补偿后相位均在0 rad左右，空变性的大气相位得到了有效的补偿。

图5 短时间基线干涉相位图A和BFig.5 Interferometric phase maps of A and B with short temporal baselines

图6 形变PS点选择Fig.6 Selection of deformation PS

图7 非线性大气相位补偿Fig.7 Non-linear atmospheric phase compensation

采用本文所提非线性补偿方法和常规的线性斜距模型补偿方法，对这459幅相位图分别分析，然后从不同斜距处选出5个幅度离差指数最小的PS点作为参考点，来对比说明本文方法的有效性。图8(a)所示为采用本文方法获取的累积相位图，由459幅补偿后的干涉相位图累加获取，该幅图像可以用来反映整个监测周期内，场景中PS点的相位变化情况。形变区域PS点的相位变化达到了约-3 rad，非形变区域PS点的相位变化在±1 rad范围内，直观上很难看出非形变区域PS点的相位是否存在空变性。图8(a)中红色方形点标识出的点1～点5为非形变区域的参考点。图8(b)所示为这5个参考点的时序相位变化曲线，点1～点5的相位变化趋势高度相似，这是由于大气相位具有较高的空间相关性。图8(c)和图8(b)所示分别为采用本文方法和常规方法对点1～点5的补偿结果。常规方法的补偿结果中，点1的相位随着时间逐渐增大，这说明了大气相位残余误差随着时间逐渐积累了起来。本文方法的补偿结果中，各点的相位序列变化更为随机。

图9(a)和图9(b)所示为采用常规方法和本文方法获取的累积相位图，为了更直观地对比场景中PS点的相位变化情况，两幅图像中均忽略了形变区域。可以很直观地看出，常规方法的补偿相位图中，PS点的相位依然呈现出明显的空变性，尤其是图像中500～600 m范围内的区域，该区域PS点的相位达到了1 rad，相应的形变量为1.48 mm。由于大气相位补偿误差随着时间积累起来的原因，这部分区域很容易被误认为在雷达监测周期内，也出现了形变。

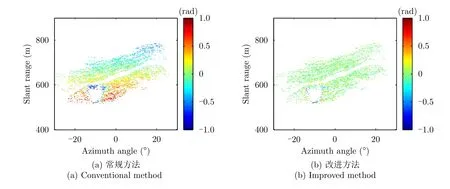
图9 累积相位图Fig.9 Cumulative phase maps

5 结束语

本文提出了一种适用于时序GB-InSAR图像非线性大气相位补偿的改进方法，解决了常规方法中多参数模型无法准确模拟大气相位，从而无法对部分干涉相位图进行有效补偿的问题。采用本文方法与常规方法，对一露天矿坑的460幅时序地基MIMO雷达图像分别进行了处理，对比了参考点的时序相位曲线和累积相位图，验证了本文方法的有效性。

本文方法还存在着一些不足。首先本文方法要求先采用常规方法对时序干涉相位图进行补偿，基于PS点的补偿后相位序列的标准差大小来选择稳定PS点，但相位标准差门限是人为设定的；其次如果部分PS点仅在少量图像中发生了形变，这些PS点的相位标准差可能较小，无法有效地筛选出；最后本文方法目前是应用于对时序GB-InSAR图像的事后大气相位补偿，实际形变监测中更关注的是实时处理，需要进一步研究实时形变处理中的非线性大气相位补偿方法。