把“提出问题”融入“变式教学”之中

石振兴

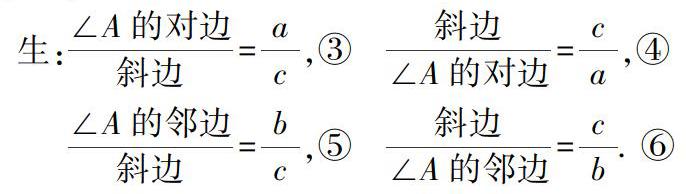
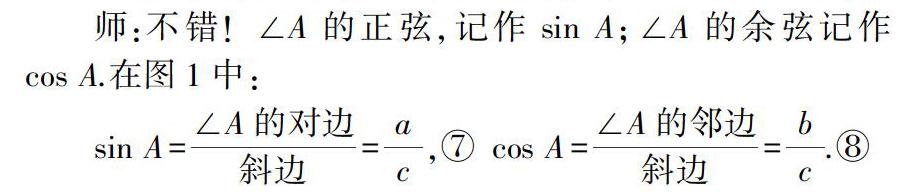
【摘要】《义务教育数学课程标准》指出：“数学教学活动应激发学生的兴趣，调动学生的积极性，引导学生的数学思考，鼓励学生的创造性思维.”同时，课程目标中也明确提出：“数学教学要培养学生的数学思维和提出问题、分析问题以及解决问题的能力”.“变式教学”应运而生，它是目标达成的重要方法.而传统的教学中，教师只重视数学知识的“变式”和数学解题的“变式”，而忽视了问题发现和提出的创新.因此，在实际教学过程中，教师把“发现问题、提出问题”有效地融入“变式教学”中，不仅能够有效地调动学会参与数学学习，更能激发学生的学习积极性，而且还可以培养学生的创新意识、创新思维和创新能力，使“教师为主导、学生为主体”的教学理念真正扎根发芽.

【关键词】提出问题;变式教学;数学课标;数学思维

一、课前分析

创新来源于问题的提出和生成，没有问题，创新就无从谈起.长期以来，我们的中学数学课堂往往只关注问题的解决，却忽视了其中更为重要的问题提出的教学，致使学生只会机械地做“答”，不会创造地提“问”.爱因斯坦说过：“提出一个问题往往比解决一个问题更重要.”因此，在实际教学中，我们不仅要重视问题解决过程中的创新，更要关注问题生成过程中的创新，把数学问题提出的训练和强化作为今后数学创新教学的“契合点”.本文是冀教版初中数学九年级“正弦和余弦”一课的教学实录，教学中突出对学生提出问题、生成问题的强化训练和培养，引导学生养成自然而然、承上启下的提出问题的习惯，强调问题的生成和升华，而不是单纯地为了问而“提问题”.

二、教学案例

（一）回顾旧知，巩固提升

师：在上一节课，我们学习了正切和余切.如图1，请指出∠A的正切和余切分别是什么？（意在通过复习正切和余切引发问题）

（生思考、回忆正切和余切的定义）

生：tan A= ∠A的对边[]∠A的邻边 = a[]b ，①

cot A=  ∠A的邻边 ∠A的对边 = b a .②

（二）借助旧知，提出问题

师：我们通过学习，知道一个锐角的正切和余切是两条直角边的比值.那么，观察图1，你还有哪些发现？有什么问题可以提出来我们共同思考、分析.（教师可以适时进行启发、引导）

（学生思考之后，举手发言）

生：图1中Rt△ABC的三条边，除了两条直角边的比以外，还能组成其他的比，比如 ∠A的对边 斜边 ，除此以外，还能得到哪些比呢？

（学生从一个极其自然、朴素的角度提出了这么好的问题，很自然地就导入到本节课所要学习的内容，这充分说明，并不像有些教师说的那样，学生不会提问题，更提不出什么有价值的问题.而是在很多时候，教师根本没有给学生创造提问题的情境和机会，只是简单地替代学生完成而已）

师：这个问题提得很好！有深度、有创意！那么，你还能组成哪些比呢？

生： ∠A的对边 斜边 = a c ，③  斜边 ∠A的对边 = c a ，④

∠A的邻边 斜边 = b c ，⑤

斜边 ∠A的邻边 = c b . ⑥

（三）问题导入，引出课题

师：很好！上面的④和⑥分别叫作∠A的余割和正割.到高中以后会进行学习，我们初中阶段暂时不做研究，但是你仍然很了不起，发现了我们今天要学习的两种“新”的三角函数：正弦和余弦.

教师板书课题：正弦和余弦.

（四）归纳概括，总结定义

师：结合上节课的学习，谁能仿照∠A的正切和余切那样，概括出∠A的正弦和余弦的定义？

生：如图1，我们把∠A的对边与斜边的比叫作∠A的正弦;把∠A的邻边与斜边的比叫作∠A的余弦.

（学生通过归纳、交流，概括出∠A的正弦和余弦的定义，其间可能会遇到些许问题，教师不要急于求成，替代学生，而应留给学生足夠的时间和空间，让学生自主完成，这也是对学生进行抽象概括能力的训练和培养的过程）

师：我们知道，∠A的正切和余切可以用其英文tangent和cotangent中的前三个字母来表示.那么，同学们你们认为∠A的正弦和余弦应当怎样表示呢？同样用正弦和余弦的英文sine和cosine中前三个字母来表示，可以吗？（可以查阅英汉词典）

（这个环节可以让学生体会到知识间的相互联系，培养学生凡事要问为什么、学习要刨根问底的良好习惯，同时培养学生的质疑能力及发现问题、解决问题的能力，从而推动学生不断成长，促进其数学素养和综合素质的有效提升.）

师：不错！∠A的正弦，记作sin A;∠A的余弦记作cos A.在图1中：

sin A= ∠A的对边 斜边 = a c ，⑦

cos A= ∠A的邻边 斜边 = b c .⑧

（五）设计问题，揭示规律

师：刚才，我们学习了∠A的正弦和余弦.那么，谁能结合上节课所学的∠A的正切和余切的相关知识，设计几个类似的问题？下面以组为单位，大家共同思考、交流，设计出一个问题，看哪个小组设计的问题最有代表性.

（教师深入到各小组，及时了解其具体进度，对有困难的小组给予引导：可以仿照正切和余切中的问题进行设计，如确定另一个锐角∠B的正弦、余弦;特殊角的正弦值、余弦值等，但最好能设计出创新性的问题：如∠A的正弦、余弦、正切、余切之间的关系.这个环节的设置可以让学生学会用类比的方法设计问题，进一步培养和提升学生提出问题的能力）

小组1：在图1中，请表示∠B的正弦和余弦.

（学生在弄清了正弦和余弦的定义的实质的基础上，结合上节课所学的正切和余切，能够提出相应的变式练习，这是非常难能可贵的，说明学生不仅掌握了所学知识，更掌握了探究问题的方法，教师应大力表扬）

师：思路很好！谁能结合图1中的Rt△ABC，确定出∠B的正弦和余弦值？

生：sin B= ∠B的对边 斜边 = b c ，⑨

cos B= ∠B的鄰边 斜边 = a c .⑩

师：比较⑦⑧⑨⑩四个式子，同学们有没有新的发现？

生：sin A=cos B，cos A=sin B.

师：在上面的两个式子中，能否只用∠A来表示？

生：因为∠A+∠B=90°，所以∠B=90°-∠A，因此

sin A=cos（90°-∠A），cos A=sin （90°-∠A）.

师：对于任意的一个锐角，是否都具有上面的性质呢？若是，你能用语言文字叙述其性质吗？

生：任意一个锐角的正弦值都等于它的余角的余弦值;任意一个锐角的余弦值都等于它的余角的正弦值.

师：你的叙述很准确，也很完整，表现真不错！

小组2：如何求特殊角30°，45°，60°角的正弦值和余弦值？

师：很好！那么你们组求出这些角的正弦值和余弦值了吗？

生：求出来了：

sin 30°= 1 2 ，sin 45°=  2  2 ，sin 60°=  3  2

cos 30°=  3  2 ，cos 45°=  2  2 ，cos 60°= 1 2 .

师：谁能代表你们组来阐述一下你们是如何求值的？

生：如图2，在△ABC中，∠C=90°，设∠A=30°，BC=a，则AB=2a，AC= 3 a，所以

sin 30°= BC AB = a 2a = 1 2 ，

sin 60°= AC AB =  3  2 ，

cos 30°= AC AB =  3  2 ，

cos 60°= BC AB = 1 2 .

生：同理，如图3，在△ABC中，∠C=90°，设∠A=45°，BC=a，则AC=a，AB= 2 a，可得

sin 45°= BC AB =  2  2 ，

cos 45°= AC AB =  2  2 .

小组3：我们学习了∠A的正弦、余弦、正切和余切，那么这几个三角函数之间又有什么关系呢？

师：这个问题提得很好，特别注重了知识之间的联系，那么，你们有什么发现吗？

生：我们知道sin A= a c ，cos A= b c ，

tan A= a b ，cot A= b a .

如果sin A÷cos A= a c ÷ b c = a b  ，而tan A= a b ，即sin A÷cos A=tan A.

同理cos A÷sin A=cot A.

师：真不错！我相信只要同学们肯动脑筋，善于观察、勤于研究，就一定能够发现数学知识的联系无处不在.我也相信努力学习、善于发现的你们潜力无限，一定能闯出属于自己的一片新天地.

（六）反思小结，归纳提升

师：本节课，我们在学习了正弦和余弦的相关知识的同时，还学到了提出问题的方法，相信每一名学生都会有所收获.那么，哪名学生能具体说一说你本节课有哪些收货？

生A：我们通过学习，发现可以用三种数学语言（符号语言、文字语言、图形语言）来表示正弦和余弦的定义和性质，并且它们之间可以转换.我觉得数学非常有趣，现在更愿意学习数学了.

生B：学习时要注意寻找数学知识之间的联系，可以运用类比的方法自己设计问题，一题多变，触类旁通.

生C：要多观察、多思考、多交流，从不和谐处找问题、发现问题、提出问题，并分析问题、解决问题.

生D：在学习时，只有善于发现问题、提出问题，才能更好地解决问题，这样不仅有助于提高我们学习数学的能力，更有助于提升我们的数学素养.

……

三、教学反思

1.新时代对广大教师提出了更高的要求，要求教师不仅要教会学生做“答”，更要教会学生提“问”.因此，在具体的教学中，教师要给学生留有足够的空间，为学生创设一个良好的学习环境，鼓励学生创造性提出问题，并逐步学会发现问题和提出问题的方法，进而培养学生分析问题、解决问题的能力.教师要相信只要给学生一个支点，他们就能撬起整个地球！

2.启发式教学注定会替代“灌输式”“填鸭式”教学，教师不能过多地替代学生，而应适时引导、启发学生发现问题、提出问题，给学生更多的发言机会，相信“创造性”火花会在课堂上形成激烈的碰撞，激发出学生的积极思维，迸发出学生无限潜能.同时，作为教师的我们也能得以提升，从而推动师生共同进步，共同成长，教学相长将不再成为空谈.

3.有学生在课后小记中写道：“这节课教师让我们自己提出问题、设计问题，我真正体会到了学习的快乐，体会到了发现的乐趣和成功的喜悦，学起来挺轻松、特来劲，原来枯燥的数学还可以这样学，我对学好数学更有信心了.”实践证明，在教学中，教师只要敢于改变，创造机会让学生主动学习、自主学习，让学生带着问题去学习，使其真正成为学习的主人，就一定能激发学生学习数学的兴趣，引导学生创造性学习，培养学生的创新意识，激发学生的创新思维，提升学生的创新能力.只有这样，“以学生发展为本”的教学理念才不会成为“空中楼阁” ，肯定会在教学中生根发芽，开出绚丽多姿的花朵.