固定/鼓泡床中煤沥青球升温过程的CFD-DEM模拟

薛嘉哲 钟文琪 邵应娟 谢立宇 李开喜

(1东南大学能源热转换及其过程测控教育部重点实验室， 南京 210096) (2中国科学院山西煤炭化学研究所， 太原 030001)

煤沥青的氧化不熔化过程是沥青基球状活性炭制备的重要环节之一，其目的是提高煤沥青球的软化点以确保其在随后的炭化活化过程中不发生熔融变形[1].在此过程中，热量在颗粒与气体、颗粒与颗粒之间相互传递，使得沥青球颗粒在合适的条件(反应器、升温速率)下缓慢升温，最终达到目标温度.目前，由于沥青球的机械强度较低，其氧化不熔化过程大多采用固定床反应器，虽保证了沥青球的结构完整，但存在氧化效率低、能耗大、易烧料等缺点[2].流化床反应器作为另一种工业常见设备，由于其具有气固间接触充分、床层温度均匀等优点而被广泛用于化工生产领域[3-4].王永邦[5]成功采用流化床反应器实现了沥青球的高效氧化，从而表明在流化床反应器上实现沥青球氧化不熔化过程的可行性.然而，在实现沥青球流化床氧化不熔化的应用前，尚缺乏对沥青球颗粒在流化床内升温传热过程的研究，沥青球颗粒在反应器内热量传递的规律及反应器结构对传热过程的影响尚不明确.

计算流体力学-离散单元法(computational fluid dynamics-discrete element method, CFD-DEM)能够跟踪气固系统内的每一个颗粒，可用于诸如流化床、炼铁高炉等稠密气固体系的模拟，并获得丰富的运动与传热信息.Hou等[6]使用2D-CFD-3D-DEM方法研究了Geldart A类颗粒的流态化传热规律；Zhou等[7]使用2D-CFD-3D-DEM方法分析了不同操作气速、颗粒导热系数、杨氏模量等条件下，流化床气固传热过程中不同传热模式的占比；Norouzi等[8]使用2D-CFD-DEM方法结合实验测量手段研究了不同高径比下，床层颗粒的混合及循环特性.上述研究能够从颗粒尺度探寻气固运动及传热的机理，从而表明了该方法在模拟稠密气固体系上的优势.然而，以往研究出于计算经济性考虑，床体往往较薄(1～5倍粒径)，其前后壁面被设置为周期性边界条件，且尚无针对沥青球颗粒在流态化系统中运动及传热过程的研究.

为此，本文利用CFD-DEM方法，建立了固定床/流化床内沥青球颗粒运动与传热过程的三维数理模型，对床层内的气固传热过程进行了研究.首先将固定床和鼓泡床中气固传热过程的数值模拟结果与实验结果进行对比，以验证本文所采用计算模型的准确性.随后对不同流型(固定床/鼓泡床)、不同高径比、厚宽比下床层内的气固流动及传热行为进行研究，获得瞬时气固流动及传热结构、床层升温速率及温度均匀性等信息，并从颗粒尺度揭示了床型结构对沥青球升温过程的影响.

1 数值模型

1.1 颗粒相模型

煤沥青球的运动过程通过牛顿第二定律描述，包括平动与转动2种运动形式，控制方程分别表示如下：

(2)

式中，mi和Ii分别为颗粒的质量和转动惯量;vi和wi为其运动的线速度与角速度;Fc,ij为周围颗粒j碰撞所产生的弹性接触力；Fd,ij为黏性阻尼力;nc为与其相碰撞的周围颗粒总数;Tt,ij和Tr,ij分别为由切向力和滚动摩擦力产生的转矩[9]；Fd为周围流体对颗粒施加的曳力.

对于气固系统，颗粒所受气固作用力包括曳力、虚拟质量力、马格努斯升力、剪切提升力等.在本文的模拟中，气固两相间的密度差较大，虚拟质量力、马格努斯升力和剪切提升力对颗粒运动的影响较小[10]，可忽略.本文考虑的颗粒i受力包括与周围颗粒j碰撞所产生的弹性接触力Fc,ij、黏性阻尼力Fd,ij、与周围流体之间的曳力Fd和重力mig.颗粒间接触力的计算公式见文献[11].

对于系统内的传热过程，本文考虑3种传热机制：颗粒-颗粒间的导热、颗粒-流体间的对流换热以及颗粒-环境间的辐射换热[6-7, 12-13].此外，本文中颗粒的毕渥数Bi<0.1，表征内部导热热阻相较于外部热阻很小，可以忽略不计，因此集总参数假设成立[7].颗粒的能量平衡可以通过如下零维方程来描述：

(3)

式中，Cp,i、Ti分别为颗粒定压比热和温度；Qij为颗粒-颗粒间的导热量；Qig为颗粒-流体间的对流换热量；Qi,rad为颗粒-环境间的辐射换热量.

1.2 气相模型

气相场基于欧拉框架，考虑气体的湍流运动，使用k-ε湍流模型将其模化.详细的控制方程表示形式见文献[14-15].

1.3 气固耦合子模型

1.3.1 曳力模型

对于本文所研究的稠密气固系统，气固曳力使用Gidaspow模型进行计算[16]：

(4)

(6)

(7)

式中，βi为动量交换系数；αg为流体的体积分数;ug、ρg和μg分别表示周围流体的速度、密度和动力黏度；Vi、di、CD、Rei分别为固体颗粒的体积、直径、曳力系数、雷诺数.

1.3.2 传热模型

本文考虑的传热机理包括：颗粒-颗粒导热、颗粒-流体对流换热[17-19].对于本文所研究的问题，其最高温度低于600 K，因此辐射换热并不显著，可以将其忽略[13,20].导热采用Chaudhuri等[21]提出的公式进行计算，表达式如下：

(8)

(9)

(10)

式中，ki、kj为颗粒i、j的导热系数；FN为作用在颗粒i上的法向力；E*和r*为两颗粒的有效杨氏模量和几何平均直径；Ti、Tj为颗粒i和j的温度；E为颗粒的真实杨氏模量；v为颗粒i的泊松比；ri、rj为颗粒i和j的半径.

对于本文研究中所涉及到的气固对流换热，采用Li等[22]提出的公式进行计算，表达式为

Qig=higAi(Tg-Tis)

(11)

(12)

(13)

式中，hig为对流换热系数；Tg为流体温度；Ai为颗粒的表面积；kg为流体导热系数；Nui为努赛尔数；Pr为流体普朗特数；n为模型经验常数，取值为3.5.

1.4 模拟对象及计算参数

如图1所示，本文的计算对象为三维矩形床，床料为直径1.2 mm、密度1 200 kg/m3的沥青小球[23].在计算前，温度为300 K的沥青球颗粒在床体上方随机生成，并在重力作用下自由下落.待所有颗粒的动能为零后，床层底部形成一个初始颗粒堆积层.随后，底部均匀送入温度为600 K的流化风，操作气速不同，床层将呈现出固定床/鼓泡床的流动形态.本文考虑了温度对气相物性参数的影响[7]，计算参数设置如表1所示.颗粒相最小流化风速计算式见文献[24].

图1 数值模拟对象的几何结构

计算时，先对三维气相场进行计算.待收敛后，根据颗粒所在位置，计算其当地网格下的流场参数(如ug、Tg等)，由此计算气固作用力、对流通量.随后计算颗粒碰撞力及颗粒间接触导热量，求解固相运动方程和能量方程从而更新颗粒的位置、速度及温度信息.待其计算完成后，再将结果传递给流场求解器，气固两相连续交替耦合求解.

2 计算结果与分析

2.1 模型验证

本文计算所采用的冷态CFD-DEM模型的验证见文献[14,25].由于本文研究涉及到固定床及鼓泡床中的气固传热过程，因此需对本文所采用计算模型中的传热部分进行验证，所参考的固定床和鼓泡床传热实验工况设置见文献 [26-27].

图2(a)为不同操作气速Uf及不同床料质量m条件下，鼓泡床中的床层平均颗粒温度随时间变化情况.可以看出，操作气速为1.54、1.71 m/s时的温降曲线与Patil等[26]的实验测量结果吻合较好，

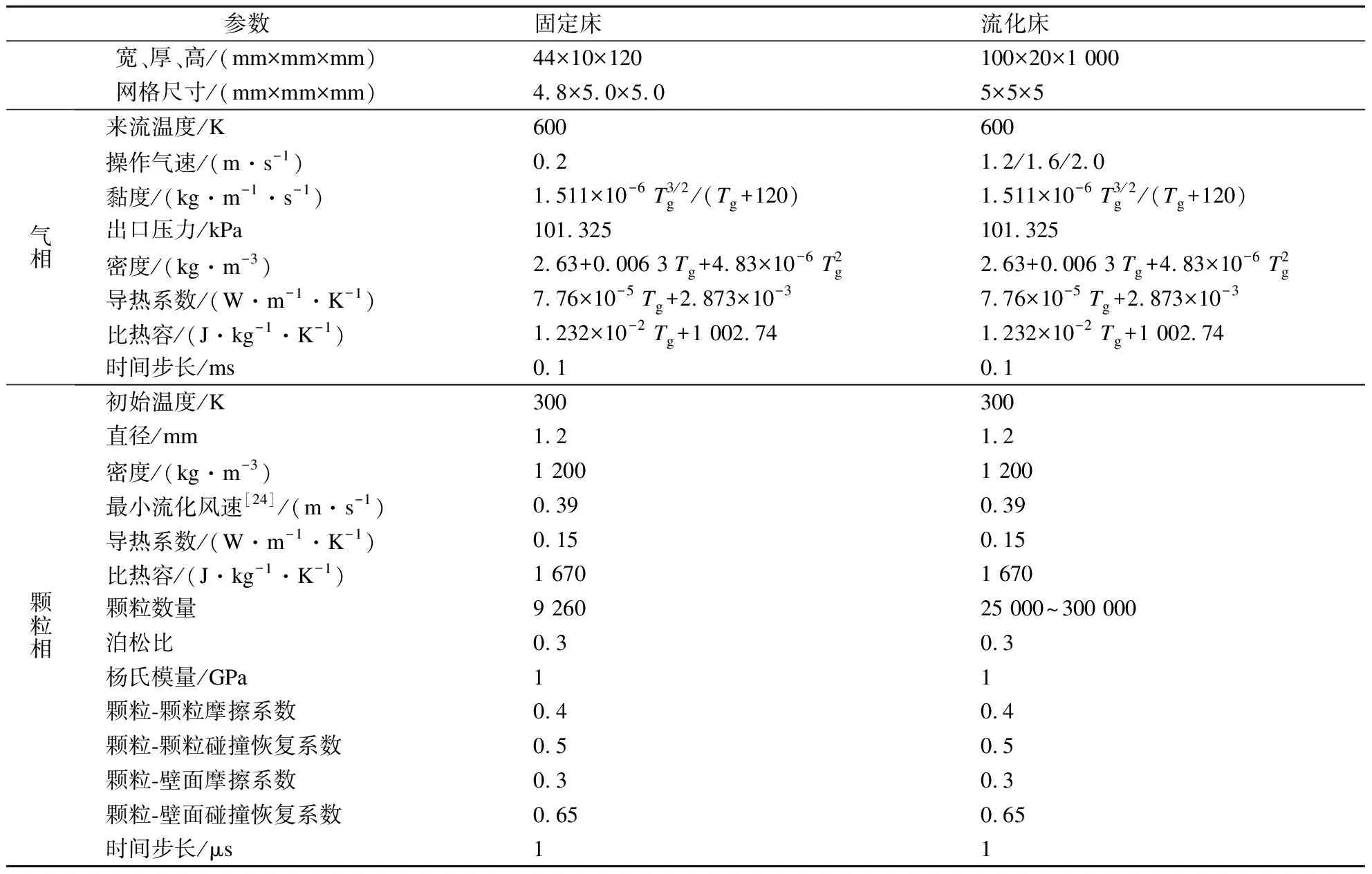
表1 模拟中使用的参数

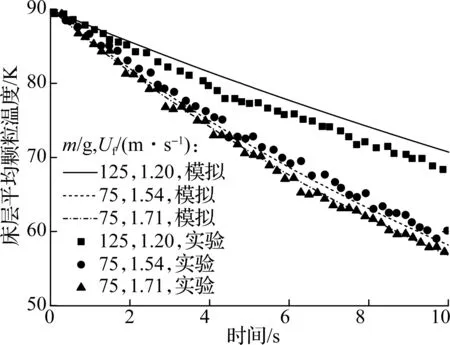
(a) Patil鼓泡床传热实验[26]

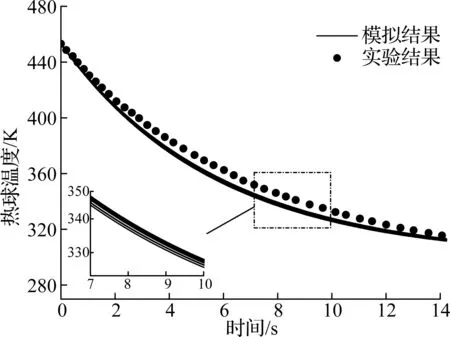
(b) Collier固定床热球实验[27]

气速为1.20 m/s时，冷却速率比实验稍慢.这与Wang等[28]、Patil等[29]的计算结果相似.Patil等[29]指出，当操作气速较低时，颗粒的瞬时停滞效应会导致颗粒间存在更长的接触时间.传热模型中未考虑这一效应导致了低气速下产生细微的误差.图2(b)给出了固定床中热球温度随时间变化，通过比较发现计算与实验结果吻合较好.值得注意的是，固定床中布置的9个热球的温度变化过程仅有微小差异，这与Zhou等[7]、Wei等[30]的CFD-DEM模拟结果相一致.

2.2 固定/鼓泡床内沥青小球的升温过程

2.2.1 固定床/鼓泡床传热过程对比

由于本文中固定床与鼓泡床的床层尺寸、床料质量、操作气速均不相同，为便于分析比较两者间的差异，本文对时间进行无量纲化处理，即以实际时间t与床层热平衡所需时间t0的比值τ=t/t0作为无量纲时间.其中床层热平衡所需时间t0通过Hou等[6]提出的公式进行估算.

图3给出了不同时刻固定床与鼓泡床中沥青小球的温度分布情况.在固定床内，不同位置处的颗粒温升并不同步，底部颗粒最先被加热至目标温度(600 K)，并在随后的时间内保持这一高温.王永邦[5]指出，这种床层内颗粒温度的不均匀性分布容易导致烧料情况的发生，对最终的成球效果造成一定影响.在鼓泡床内，床层底部气泡的裹挟作用和上部颗粒的返混作用共同使得床层内颗粒能够均匀地得到加热，床内的温度分布更均匀.

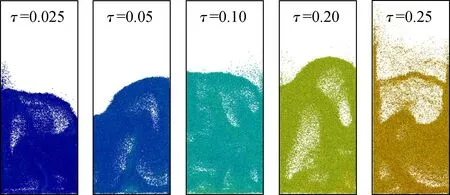
(b) 鼓泡床(ug=0.2 m/s)

图4定量表征了固定床与鼓泡床中，沥青小球的传热特性及其随时间演化规律.从图4(a)、(b)中可以看出，2种床型中发生气固对流传热的位置不同：①固定床中的气固对流换热最早发生在床层底部，待底部气固传热达到热平衡后，对流换热发生的位置逐渐上移.由于气固间温差降低，峰值水平也随之下降.②而鼓泡床内的对流换热则始终发生在床层底部Y/H0=0～0.3这一范围(约20 mm)内，这与文献[31-32]的研究结果较为一致.

由图4(c)、(d)中2种床型下颗粒的温度分布可以看出，固定床中不同位置处的颗粒温升具有明显的不同步性，靠近底部的颗粒温升更快；而鼓泡床内的轴向温度分布较之固定床明显更为均匀，整体上呈现出有效传热区-均匀温度区-抛洒区的分布规律.其中，有效传热区表征床层底部剧烈的气固对流传热作用，抛洒区表征上升气泡对底部高温颗粒的裹挟作用，而均匀分布区则表征鼓泡床内良好的颗粒返混效果.

图4(e)、(f)为2种床型下的床层平均温度及温度标准差随时间演化情况.从图中可以看出，2种床型的温升斜率均随时间推移而平稳下降，这是由于气固间温差降低，传热的驱动力减弱所导致.对于温度均匀性而言，两者均表现为先升后降的变化趋势.值得注意的是，由于鼓泡床内良好的气泡掺混效果，其温度标准差明显低于固定床，表明其具有更好的温度均匀性.

图5给出了固定床及鼓泡床中，某一跟踪颗粒的轴向坐标、温度及对流传热通量随时间变化情况.由图5(a)中可以看出，固定床内3个高度(Y/H0=0.02、0.6、0.9)处跟踪颗粒的对流传热通量均呈现先增后减的变化规律.到达峰值的时间随颗粒所处高度的增加而延后，峰值水平也随之逐渐降低.由图5(b)可知，鼓泡床内的跟踪颗粒温升主要发生在其进入底部区域的时间段内(τ=0.02～0.03、0.052～0.058、0.075～0.076)，且颗粒越靠近底部布风板，其温升越大.当颗粒处于床层中上部时，对流传热并不强烈，这与图4(b)的对流通量分布结果相吻合.

2.2.2 高径比的影响

从图6可以看出，气泡的生长、合并现象随床层膨胀高度的增加而逐渐明显，床层整体温度水平也因热容量的增加而有所降低.对于图6(a)的浅床流化床，床层内同时存在2个细长高温带状结构，这是由于堆积高度较低(H0/b=0.38)时，气泡趋向于从床层中心的两侧生成，固相的内循环模式发生变化所致[8].

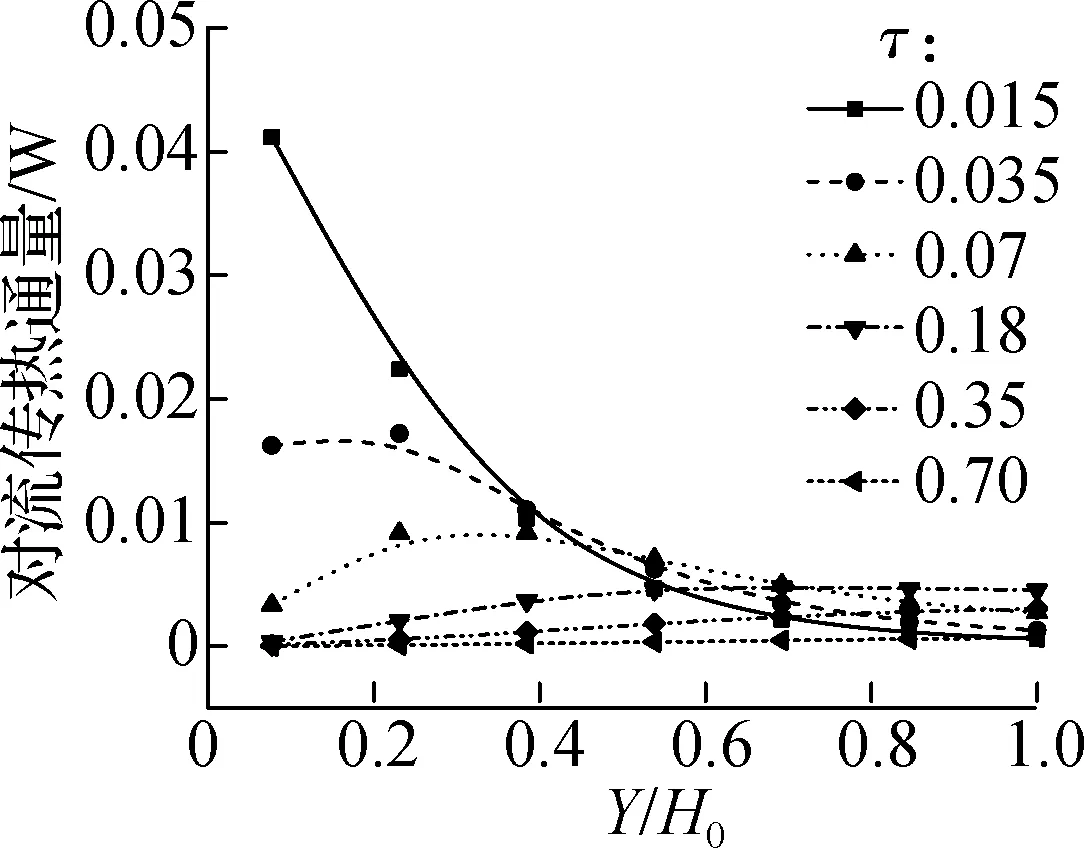
(a) 固定床对流传热通量沿轴向分布

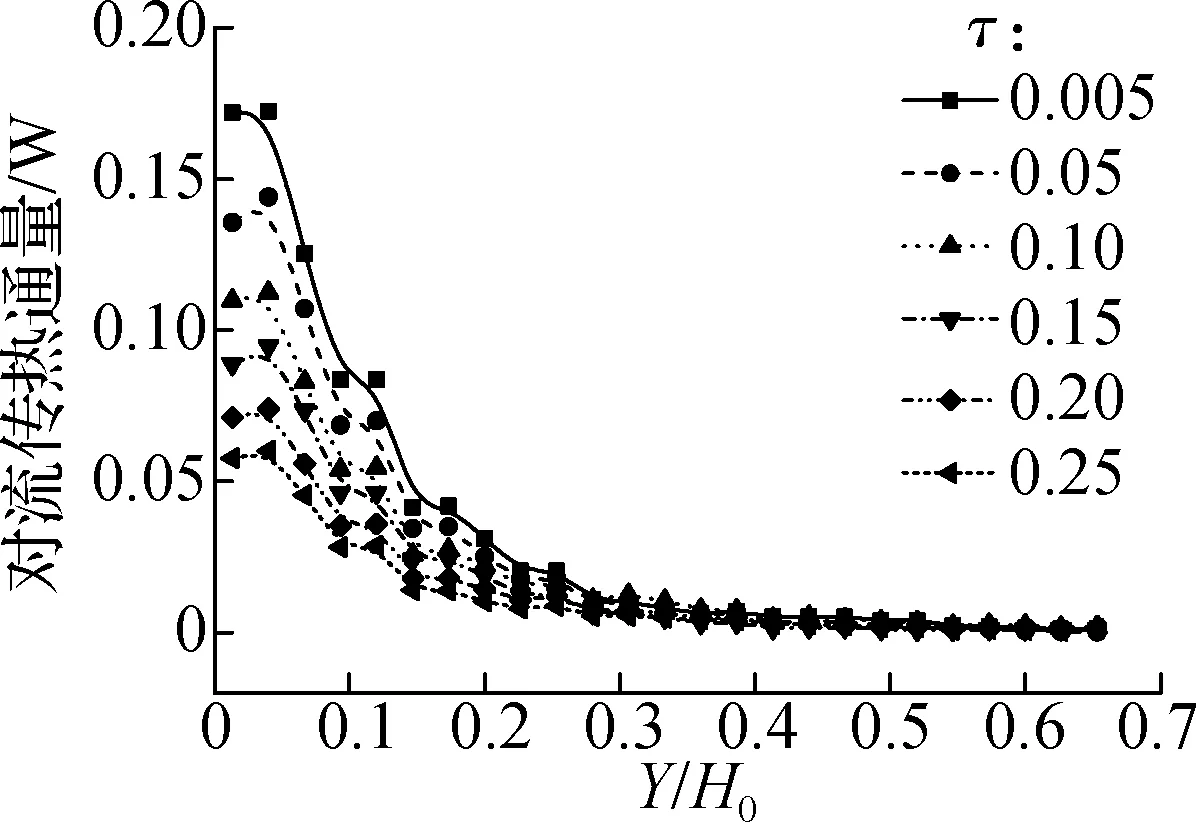
(b) 鼓泡床对流传热通量沿轴向分布

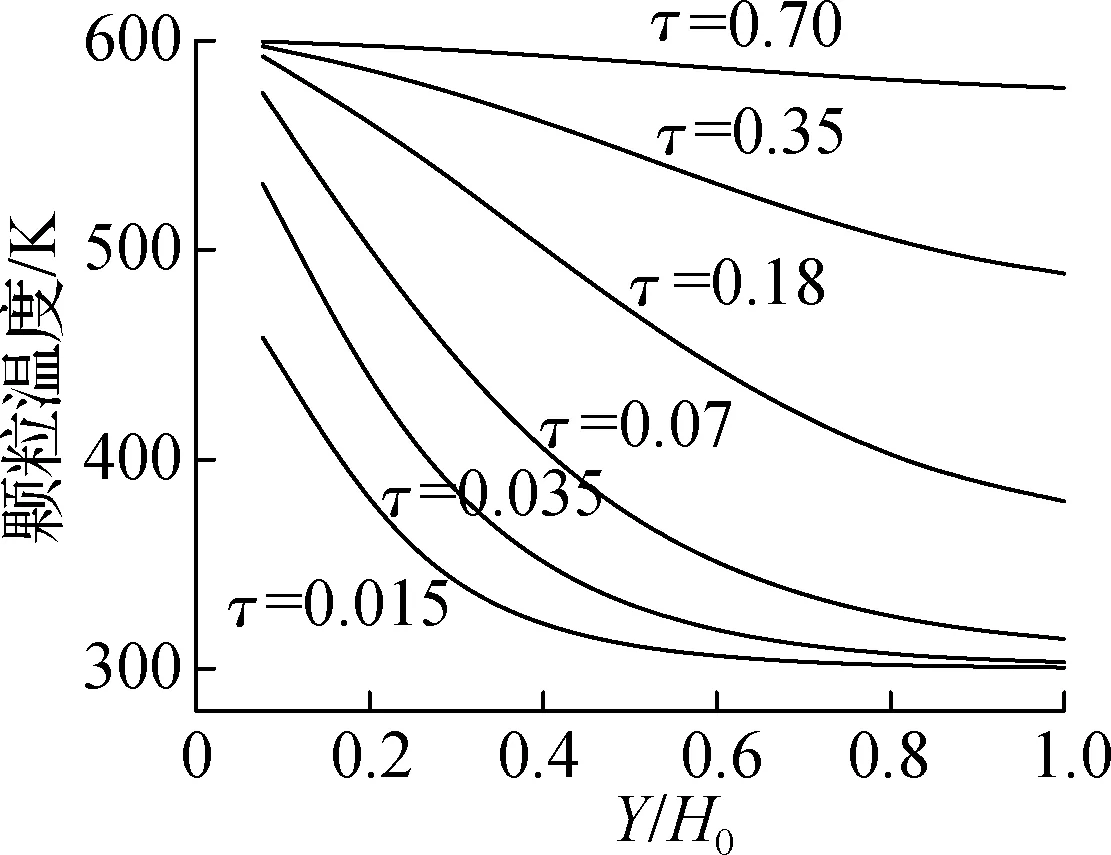
(c) 固定床温度沿轴向分布

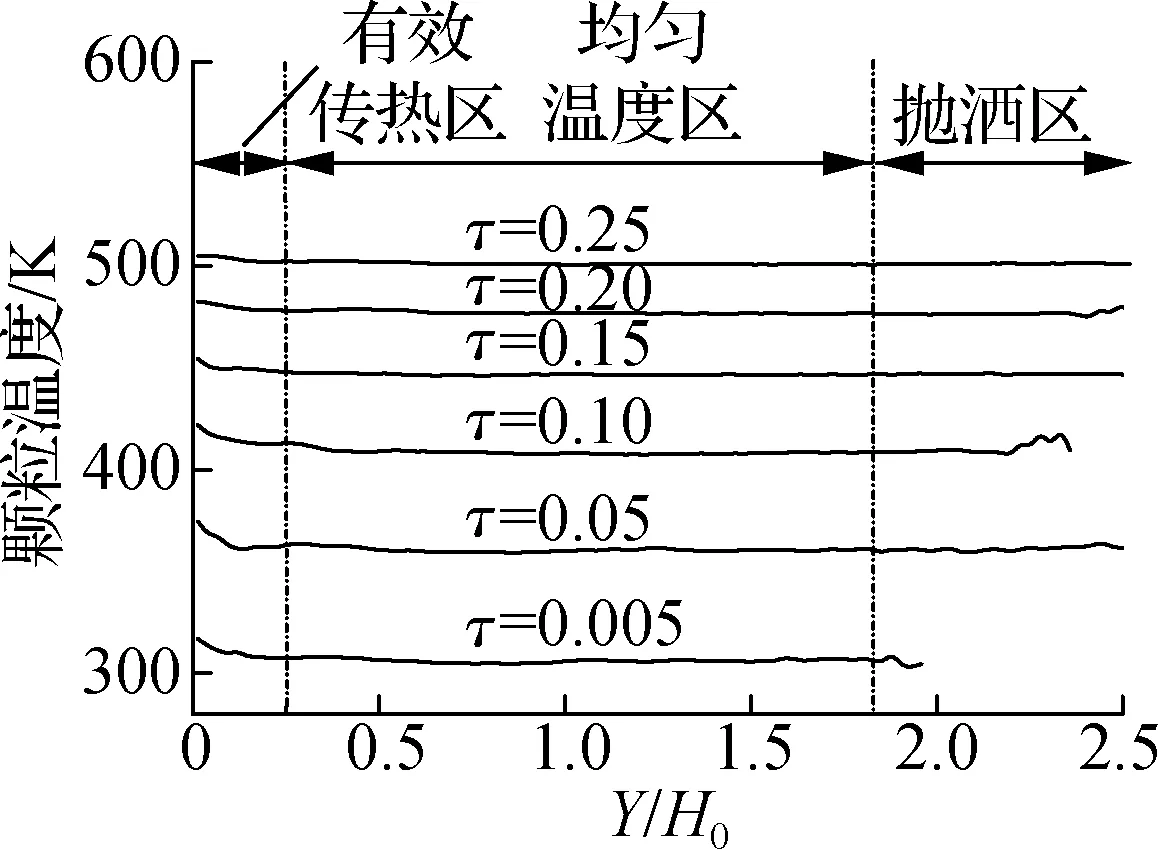
(d) 鼓泡床温度沿轴向分布

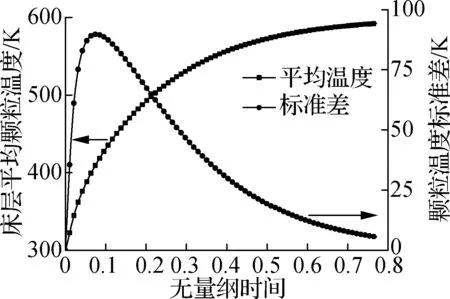
(e) 固定床平均温度及标准差随时间变化

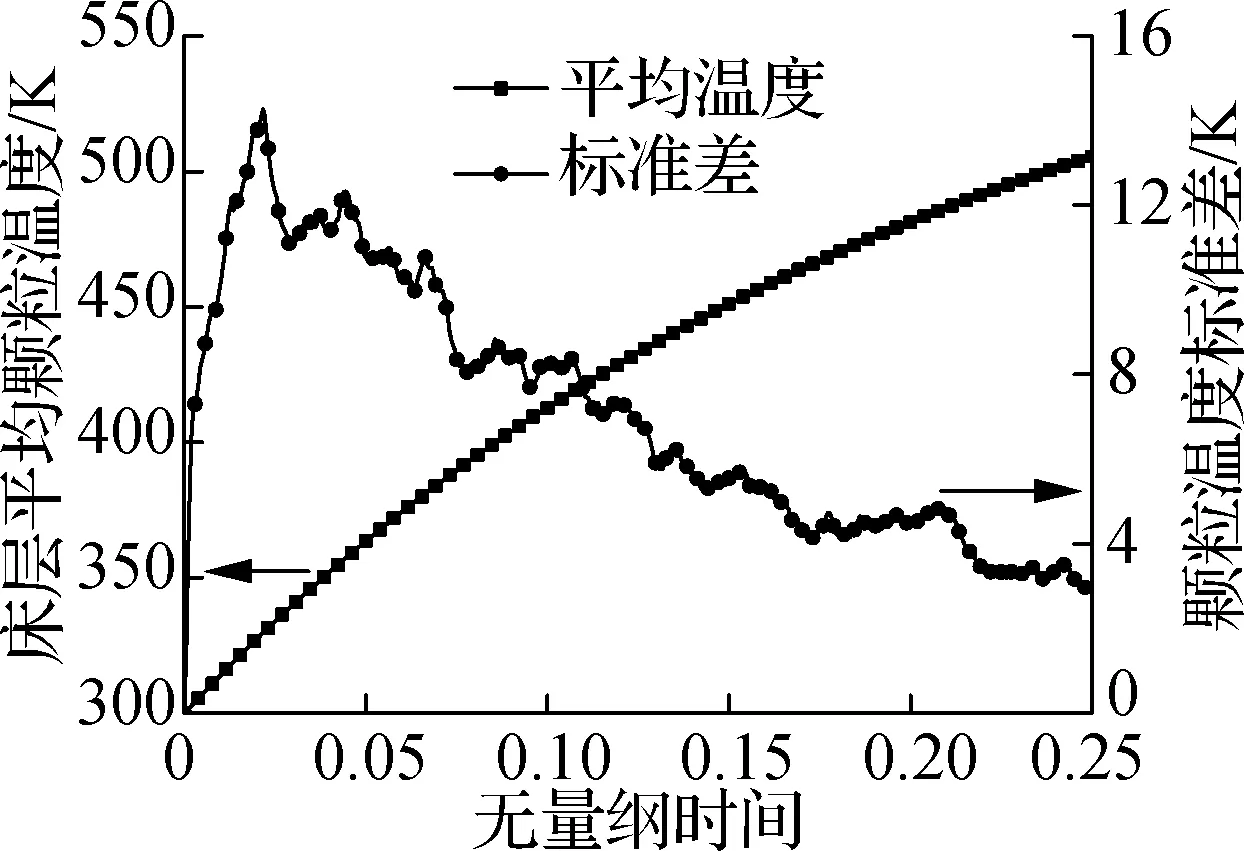
(f) 鼓泡床平均温度及标准差随时间变化

(a) 固定床

(b) 鼓泡床

图7给出了不同高径比下升温速率及温度均匀性的定量比较结果.从图7(a)中可以看出，高径比提高，床层升温速率随之下降，但其下降的幅度与高径比提升的幅度之间并非线性关系.进一步观察图7(b)可以发现，当高径比提高至0.95左右时，升温速率的降低幅度已经很小.这说明有效气固传热距离并不随堆积高度发生明显变化.此外，从图7(c)的温度标准差随时间变化情况可以看出，床层温度分布随高径比的降低而变得更加均匀，但当高径比较大时，均匀性差距也并不明显.

为从颗粒尺度解释高径比与颗粒运动、传热之间的内在关系，图8给出了3种高径比下，底部中心处跟踪颗粒的运动及传热情况.由图可以看出，高径比的增加提升了跟踪颗粒的平均上升距离，从而使得颗粒进入底部区域的频率降低.这直接导致流传热通量峰值出现的频率降低，并最终体现为图8(c)中颗粒升温速率的降低.

(a) H0/b=0.38

(b) H0/b=0.57

(c) H0/b=0.76

(d) H0/b=0.95

(e) H0/b=1.14

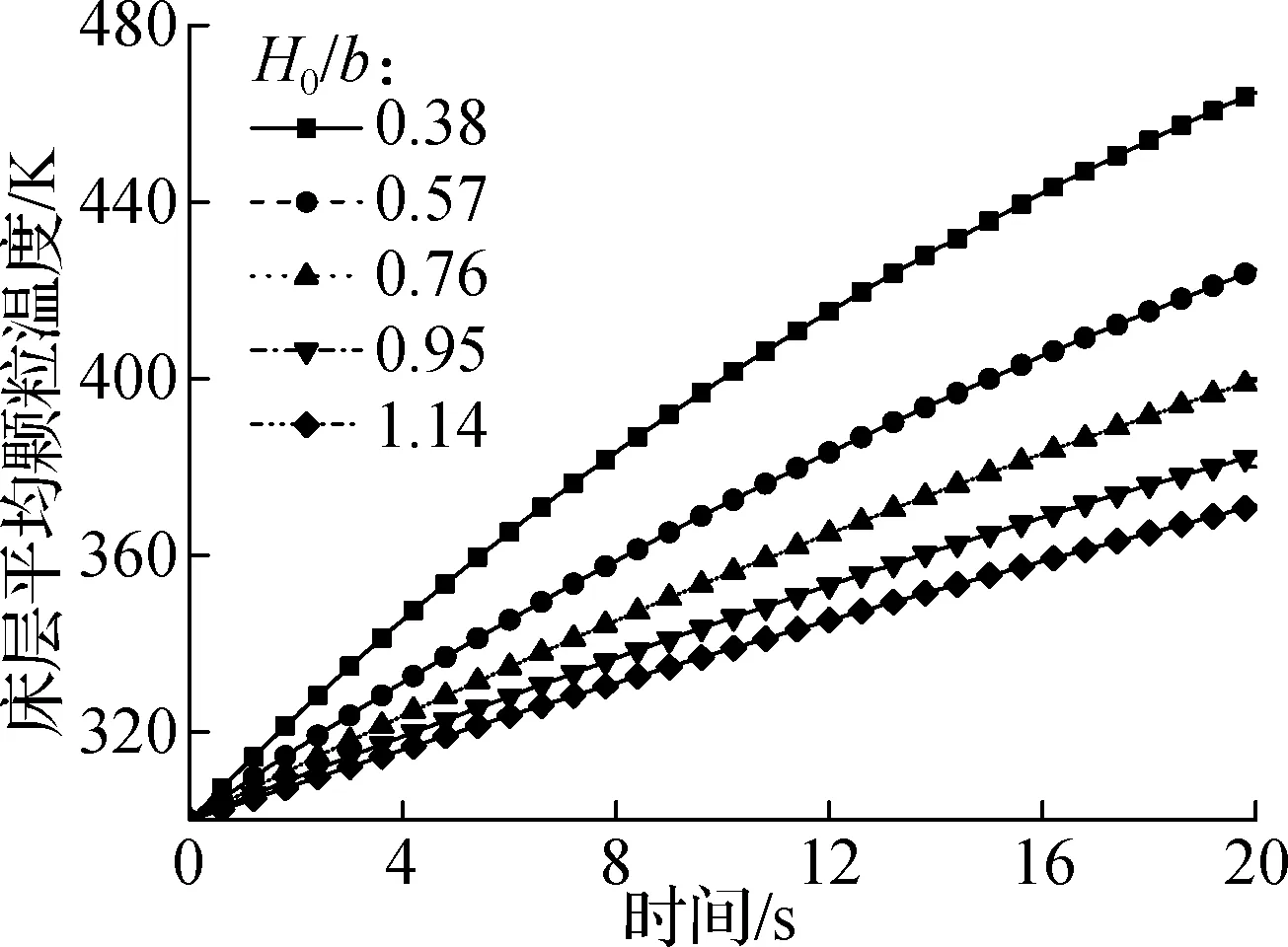
(a) 床层平均温度

(b) 不同高径比间的相对变化趋势

(c) 温度标准差

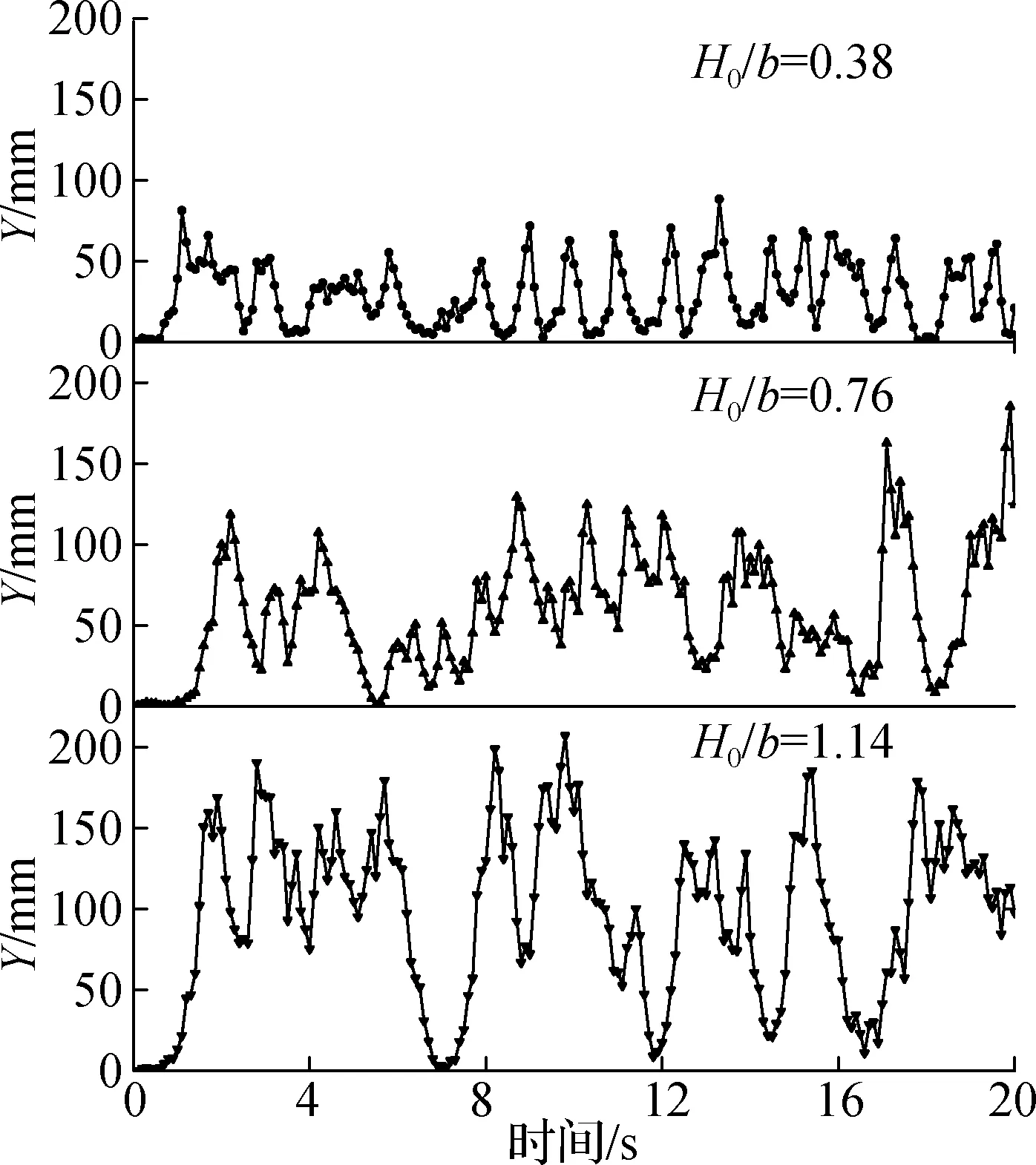
(a) 轴向坐标随时间变化

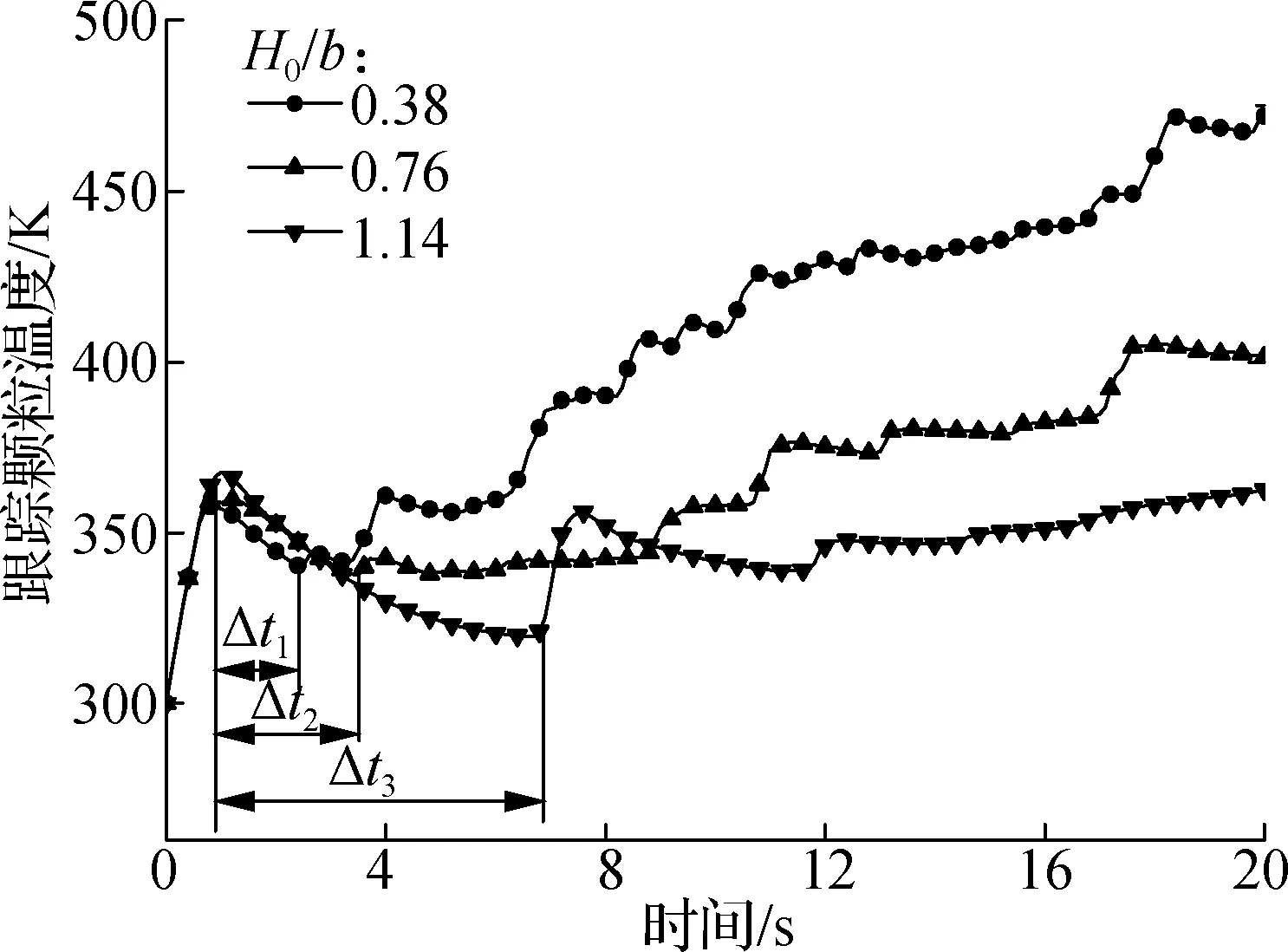
(c) 温度随时间变化

此外，跟踪颗粒在传热初始阶段出现了一定的温降，且其时长随高径比的增加而增加(Δt3>Δt2>Δt1).对此现象，本文认为：①通过前文分析可知，对流换热主要发生在床层底部(见图4(b))，当流体经过床层底部后，其温度已与床层中上部冷颗粒的温度相当；②跟踪颗粒在床层底部被空气加热后，受气泡裹挟作用而向上运动.在此过程中，其周围的流体温度已低于受到加热的跟踪颗粒本身的温度，因此其受到低温空气的冷却而出现温降.随高径比增加，颗粒在床层中上部区域的停留时间越长，其与低温空气发生对流换热的时间越长，从而出现了更大的温降.

2.2.3 厚宽比的影响

Geldart[33]指出，由于壁面效应的存在，准二维流化床在气泡尺寸、上升速度、破碎频率上与三维床存在一定差异.为进一步探究鼓泡床厚宽比对气固流动及传热的影响，本节将前文使用的床层厚宽比由0.2提升至0.6，以探究两者在传热特性上的差异.

图9给出了厚宽比为0.6时气泡形状(定义为αg=0.75等值面气泡边界)、中心剖面(Z=0)处的固相速度矢量Vp及Y方向动能随时间的变化情况.

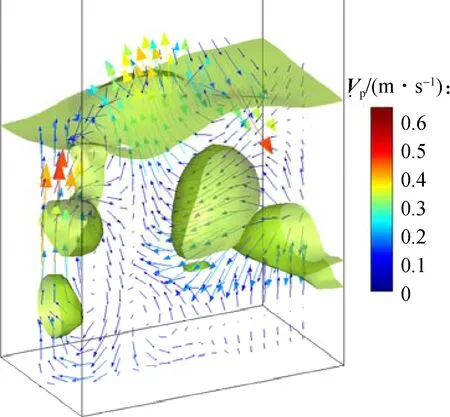
(a) 气泡形状及固相速度矢量

(b) Y方向颗粒动能随时间变化情况

可以观察到此时气泡形状呈现出强烈的三维特征.通过图9(b)的颗粒动能可以看出，δ/b=0.6时的平均动能较之δ/b=0.2时提升约46.3%.这是由于厚宽比增加使得壁面效应减弱，气泡上升速度提高[34-35].此外，不同厚度下的颗粒Y方向速度均随时间稍有增加，这是由于温度变化导致的气相物性参数变化所致.

图10给出了2种厚宽比下床层平均颗粒温度及标准差的时间演化情况.利用Hou等[6]提出的平均升温速率表达式对图10(a)中的升温速率进行统计可以发现，三维床相较于准二维床，其升温速率提高了24.2%.对此现象本文认为：气泡上升速度的增加能够更快地将高温颗粒带离底部区域，同时床层中上部的低温颗粒将返混至底部区域得到加热，从而提高了底部区域气固间的温差.当忽略颗粒间导热时，由颗粒升温过程的热平衡方程

可知，气固温差越大，传热的驱动力越大，颗粒温升也越大.

从图10(b)可以看出，在计算初始阶段，底部空气的加热打破了初始床层的温度均匀性，使得温度标准差从零迅速提高.且床层厚度增加导致的升温速率加快提高了标准差的峰值.在随后的标准差下降过程中，三维床的下降幅度略高于准二维床，这可能是由于三维床更为强烈的气泡掺混作用所致.

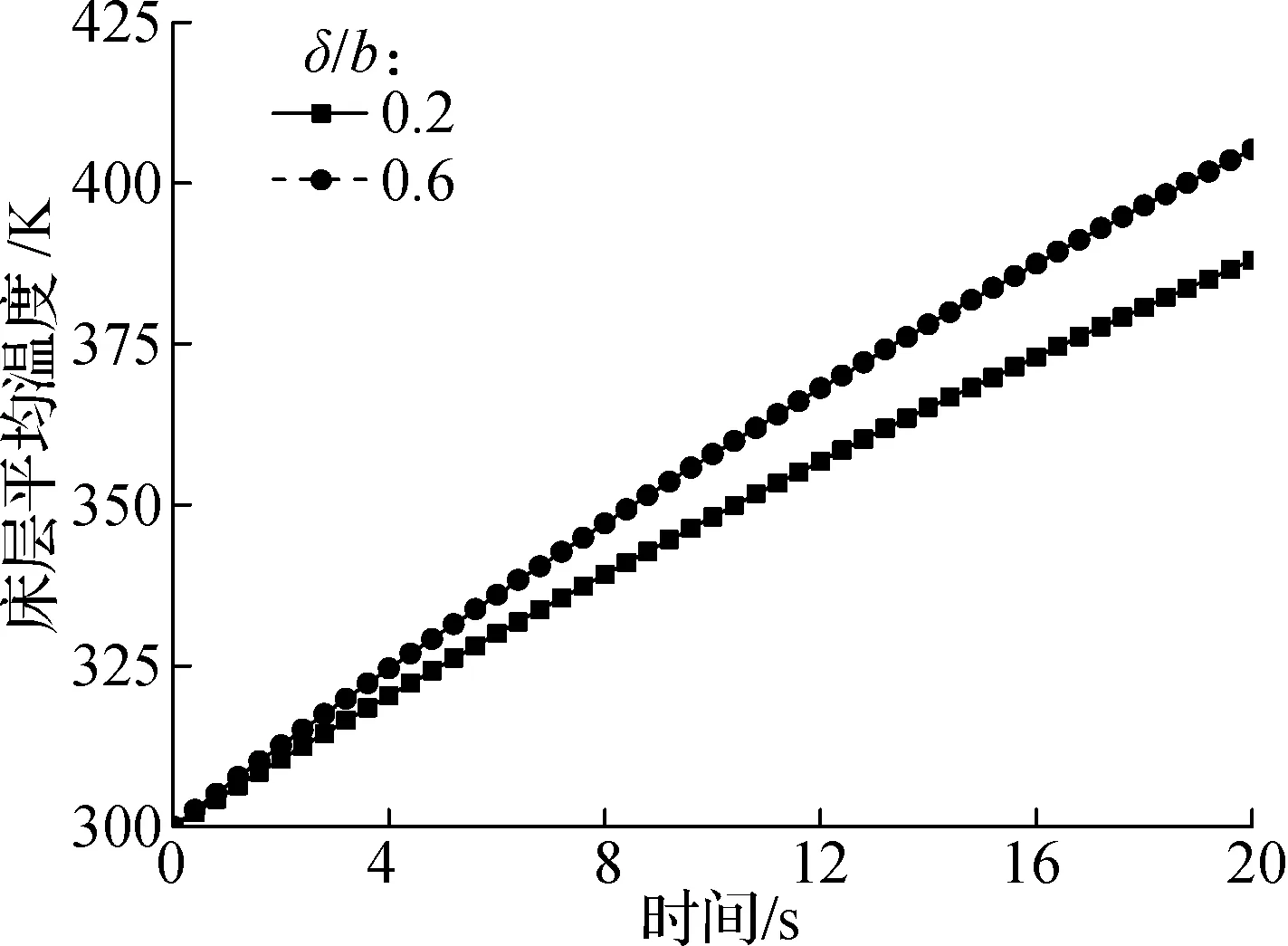
(a) 床层平均温度随时间演化情况

(b) 温度标准差随时间演化情况

3 结论

1) 在固定床中，沥青颗粒温升从床层底部逐渐向上传递，颗粒沿轴向存在明显的温度梯度，床层底部颗粒长时间处于高温状态；而采用鼓泡床反应器，底部被加热的颗粒能够及时被上升气泡带离底部区域，避免了局部高温区域(烧料现象)的形成.

2) 当高径比提高至0.95以上时，其对鼓泡床温升的影响较小；随高径比的提高，跟踪颗粒在床层上方受到低温空气冷却的时间增加，从而出现了更大的温降.

3) 随厚宽比的增加，壁面效应的影响减弱，气泡上升速度、颗粒动能均有所增加，且床层颗粒的内循环速率加快，床层底部气固间温差有所增加，床层颗粒升温速率提升约24.2%.