基于ADAMS的内埋式导弹发射俯仰角变化仿真分析
2020-01-15
(海军航空大学岸防兵学院, 山东烟台 264001)
引言
自上世纪末,世界各军事强国均开始着手新型空中力量的研制。随着战机性能的不断发展,战斗性能的隐身性也就成为了制约胜利的关键因素之一[2]。为了保证战机隐身性,这代战机配备的空载导弹多采用内埋式挂装,并要求满足迅速弹射,不影响载机隐身性[3]。而内埋挂装弹射时,导弹在弹射后必须有一个负向的发射角速度以保证发射俯仰角向下,即导弹低头,否则很有可能导致机毁人亡[4]。本研究基于ADAMS对机载导弹内埋式发射系统进行动力学研究,验证其发射安全性,具有一定的指导意义。
1 弹射装置简易原理图
弹射系统原理模型由上下梁、前后转动臂、同步杆等组成[5]。发射装置由气液系统提供动力,弹射时由高压气体供能液压管路,带动前后转动臂展开,将导弹弹射出去,同时水平活塞杆保证前后摆臂的动力和同步性。
导弹弹射时气液系统提供瞬时大排量的高压液体,使弹射装置展开[6]。为了保证弹射装置的结构强度,必须使其中的部分结构满足一定的弹性形变,保证其柔性特性。因此支臂杆5,7设定为柔性处理后的细长杆,其余部分需要保持一定刚度,故不做处理。
弹射装置中各杆、摆动臂自由度关系:上梁与机舱连结,视为固定;摆动臂与活塞杆之间为轴转动副;作动臂与下梁为轴转动副;支臂两端均为轴转动副。

1.上梁 2.液压动力缸 3.水平活塞杆 4.摆臂1 5.支臂1 6.摆臂2 7.支臂2 8.导弹图1 弹射装置简易模型
2 建立系统动力学方程
导弹弹射系统是一个多体系统,其中既包括多自由度的刚体运动,也包含发生弹性形变的柔体运动[7]。因此,我们用来建立数学模型的理论基础是第一类拉格朗日方程。
具有完整理想约束的有N个广义坐标系统的拉格朗日方程的形式是[8]:
(1)
式中,qr—— 第r个柔性体广义坐标
E—— 系统动能
U—— 系统势能
Qr—— 对第r个广义坐标的广义力
式(1)的约束方程为:
ψs(q,t)=0
由于设定的系统中存在柔性部件,故可设弹性形变引起的做虚功为:
δWe=-KqTδq
(2)
其中,K为对应qr的刚度矩阵。
相对应的构件动能为:
(3)
将式(2)、式(3)代入式(1)中,得到:
(4)
式(4)中,为出弹性形变力以外所有主动力的广义力。
则可得建立的动力学方程为:
ψs(q,t)=0
(5)
3 动力学仿真分析
3.1 动力学模型仿真结果
导弹发射时,弹体分离俯仰角速度变化和俯仰角度是发射分离时的主要参数[9]。分离时,速度快慢直接影响弹体脱离载机的时间长短,角速度则直接影响分离安全,若俯仰角为0或者正值,则说明导弹在分离时“抬头”,在发射过程中很容易导致导弹与载机相撞从而引起严重事故,因此必须保证弹体完全分离后,俯仰角为负。
图2可见,某型导弹弹射从开始到弹架分离用时约0.06 s,分离末端速度约8.1 m/s[10]。

图2 导弹分离时间与速度曲线
图3为俯仰角速度ω仿真曲线。其中,曲线1为本实验仿真采用的刚柔耦合模型曲线,曲线2为不设计柔性构件得到的仿真曲线。图中可见,纯刚体结构其角速度一直负增加,导弹持续“低头”;而刚柔耦合构件其角速度先负增长后在弹射时间点2/3处开始回弹,呈现先“低头”后“抬头”的趋势。在实际样机的试验中,我们得到的曲线基本与曲线1一致,故可得弹射装置中会产生一定的弹性形变力,采用刚柔耦合的模型能够基本模拟实际弹射情况。

图3 不同模型弹射时俯仰角速度曲线
3.2 设计参数对发射俯仰角的影响
1) 弹射行程的影响
从上节分析中可以得知,我们所设计的模型在0.06 s时结束弹射过程,由图4、图5又可得知在0.06 s 内,导弹俯仰角持续负增长,不过增长的幅度由快减慢[11]。但在0.071 s时,导弹弹射时俯仰角速度由负变0,在接下来的时间里导弹开始“抬头”,此时对应的弹射行程为350 mm,即若发射装置弹射行程设计超过350 mm,则可能引起严重的安全问题,故设计时的约束行程不得超过350 mm。

图4 俯仰角速度曲线

图5 导弹弹射位移曲线
2) 改变柔性构件组合
本研究仿真中采用的刚柔耦合模型与实际试验的测试曲线基本相符,为了验证其他模型,我们更改了仿真模型中其他构件的参数:
曲线1:多刚体(设置模型所有组件均为刚体)模型下的俯仰角速度曲线;
曲线2:多柔体(设置模型所有组件均为柔体)模型下的俯仰角速度曲线;
曲线3:刚柔耦合模型下的俯仰角速度曲线。
从图6中可以看出:多刚体模型角速度一直呈现负增长的趋势,虽然能够满足一直“低头”的要求,但是与实际情况并不符合。
多柔体模型下分离俯仰角速度呈现近似弦曲线的变化上下波动,其角速度变化很不稳定[12],无法保证其姿态维持在“低头”状态,故弹射装置必须保证足够的刚度。
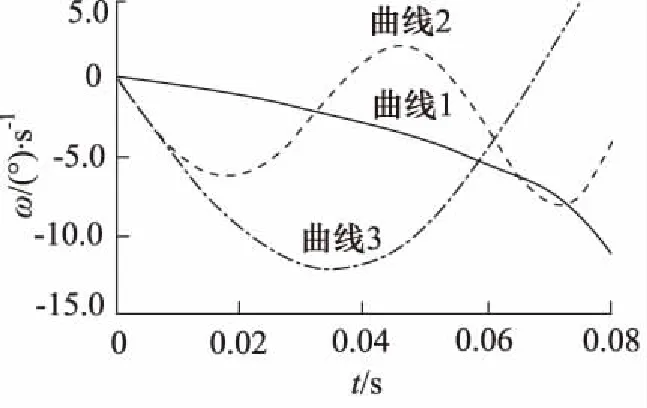
图6 不同模型俯仰角速度曲线
刚柔耦合模型与实际情况基本相符,在保证满足要求的行程下,导弹“低头”趋势由快渐缓,但能够保证在完全分离后持续的“低头”,满足导弹弹射的要求。
4 结论
(1) 导弹弹射装置弹射过程可由拉格朗日方程建立模型,计算时需要考虑弹性力做功,仿真实际的弹射过程。弹射装置同步杆具有一定的弹性形变,多刚体模型并不能反映实际的弹射环境;
(2) 在本次仿真中设计的导弹弹射行程不能超过350 mm,若超过该行程则导弹可能出现“抬头”的情况,继而引发与载机相撞的危险;
(3) 多刚体模型能保证安全但与实际不符;多柔体模型俯仰角速度变化很不稳定,弹射装置需要一定的刚度[13];刚柔耦合模型能基本反映实际的导弹姿态情况,具有一定的实验指导性[14]。
