六自由度电液振动台矩阵控制方法误差分析

2020-01-15

液压与气动 2020年1期

(大连海事大学机械工程系，辽宁大连 116026)

引言

电液振动台刚度大，精度高，可产生较大输出力，常用于研究和检验产品在振动条件下的结构可靠性和操纵可靠性[1-2]，例如日本防灾科学研究所研制的E-Defense多轴振动台[3]。对于多自由度振动台控制的控制策略，以往多采用合成/分解矩阵进行铰点空间与自由度空间之间的信号转换[4]。目前振动台多为正交结构布置，普遍采用矩阵控制算法，该算法平动自由度偏差小，能很好的完成平动自由度的振动环境模拟。

随着振动环境试验的复杂化，平动自由度的振动模拟往往不能满足复杂的振动环境要求，需要振动台完成转动自由度甚至多自由度复合运动。多自由度振动台系统是一多变量和本质非线性的复杂系统，系统运动精度至关重要[5]。精确的运动学解算有利于提高系统的控制精度。运动学主要研究各驱动器运动规律和平台运动规律之间的关系，是系统设计、驱动器设计和研究系统控制策略的基础[6]。目前振动台控制策略还普遍采用矩阵算法，该算法相对于运动学算法存在一定的误差，影响控制精度。因此对矩阵算法的误差进行量化的分析，对控制算法的优化与改进具有一定的指导意义。

本研究分析了六自由度振动台矩阵算法与运动算法的原理，并对矩阵算法的误差与产生的自由度耦合进行了仿真及实验研究，在此基础上对矩阵算法与运动学算法的特点进行了对比分析。

1 六自由度振动台结构

六自由度振动台实体图及结构简图如图1所示，结构参数如表1所示。该振动台采用正交结构布置，水平向3个液压缸(图中1～3)连接平台(图中10)与反力支座(图中7～9)、垂直向3个液压缸(图中4～6)与平台和底座相连。

为了描述平台的运动，在平台中心构建2个坐标系，静坐标系(Oxyz)和体坐标系(O′x′y′z′)。其中体坐标系与平台固联，其坐标原点位于水平向激振器上铰点构成的长方形平面的中心，静坐标系固定在大地上。在平台处于中位时，静坐标系与体坐标系完全重合，当平台运动时，体坐标系随平台一起运动，而静坐标系始终静止不动。六个运动自由度分别为沿x,y,z轴的3个平动自由度px,py,pz以及按3-2-1顺序旋转的欧拉角Rz,Ry,Rx。

表1 振动台尺寸参数 m

2 传统矩阵控制

图2为六自由度振动台传统矩阵控制系统[7]。其中的自由度分解矩阵与自由度合成矩阵可以实现自由度空间与铰点空间信号的近似相互转换。

图2 传统矩阵控制策略

设第i个液压缸的伸缩量为Δli，当平台位姿Q=[px,py,pz,rx,ry,rz]T(px，py，pz为平动位移量，m；rx，ry，rz为转动角度，°)较小时，根据振动台系统各液压缸的分布及参数尺寸可得[8]：

Δl1≈px

Δl2≈py+d3·rz

Δl3≈py-d3·rz

Δl4≈-pz+d1·rx-d2·ry

Δl5≈-pz+d2·ry

Δl6≈-pz-d1·rx-d2·ry

(1)

写成矩阵形式：

简写为：

ΔL=Hf·Q

(3)

其中,Hf为分解矩阵，合成矩阵为分解矩阵的逆：

(4)

根据零位线性化(sinx=x)的假设推导出自由度合成及分解矩阵，其局限性就是矩阵元素在控制运动过程中保持不变，并且平台运动位姿应在初始位姿附近。当系统运动位姿较大时，这种基于零位线性化的方法推导的自由度合成信号、分解信号与实际系统的信号相比有较大的偏差，从而降低了振动台系统的控制精度。

3 基于运动学分析的控制策略

六自由度振动台系统基于运动学分析的控制策略如图3所示，通过对位姿、速度及加速度进行运动学分析推导出液压缸信号与自由度信号的实时代数关系，以替代传统的分解/合成矩阵。

图3 运动学控制策略

3.1 速度、加速度正/反解算法

六自由度电液振动台是一种典型的并联机构，关于并联机构的位置正/反解算法可参考文献[9]、文献[10]。这里对速度与加速度的正/反解算法作一些补充。

振动台上平台的空间六维速度与各液压缸伸缩速率之间有如下关系[5]:

ΔL′=J·[P′ω]T

(5)

(6)

式(5)反映了振动台速度与液压缸速度的实际数量关系。对式(5)求时间导数可得：

(7)

其中, ΔL″为各液压缸伸缩加速度；P″为平台3个平动自由度线加速度；ω′为平台3个转动自由度角加速度。

3.2 雅克比矩阵的时间导数矩阵

由式(6)可得：

(8)

由式(8)可知雅克比矩阵的时间导数矩阵可以分为两个部分。第一部分是液压缸单位矢量方向的时间导数；另一部分是叉乘部分的时间导数。

第i个液压缸的单位矢量方向等于液压缸下铰点到上铰点的矢量方向除以此时的液压缸长度，即：

(9)

对式(9)求时间导数：

(10)

式(10)中L′i为液压缸矢量的时间导数，因此等于该液压缸上铰点的速度，根据速度合成定理，绝对速度等于牵连速度加上相对速度，有：

(11)

式(10)中|Li|′为液压缸长度的时间导数，因此等于液压缸的伸缩速度，即：

|Li|′=ΔL′

(12)

由MERLET[11]文章中的叉乘求导结果可得：

(13)

将式(10)、式(13)带入式(8)即可得雅克比矩阵的时间导数矩阵。

基于运动学分析获得的自由度空间与铰点空间的转换关系是一种精确的数学模型，运动学算法的解算误差可以忽略不计，该算法极大的弥补了传统矩阵算法中的解算误差，尤其是平台大位姿时的解算误差。

4 实验研究

实验所用的六自由度电液振动台如图4所示。主机与目标机之间的通信通过网络连接实现，振动台系统与目标机通过I/O设备连接，其中信号处理单元与伺服阀及各传感器相连，实时采集并处理各个液压缸的位移、速度及加速度。控制系统基于Simulink RTW/XPC平台构建，实现对系统的实时监控[12]。利用Simulink/XPC在主机上搭建振动台系统控制模型，通过RTW将振动台系统控制模型生成C代码，通过以太网将生成的执行代码下载到目标机中，进而实现在主机上进行实时调试、在线调整参数的目的。

图4 六自由度电液振动台试验系统

矩阵算法的解算误差随工况不同而变化。本研究分别对平动自由度pz与转动自由度rx这两个具有代表性的单自由度进行试验研究。首先通过低频大位姿试验研究了矩阵算法的位置解算法误差与产生的自由度耦合。对于矩阵算法的加速度解算误差，由于振动台系统的运动范围受液压缸的性能限制，当平台做正弦运动时，不同频率下平台所能达到的最大位姿有限，而矩阵算法的加速度解算误差与平台实际位姿有关，因此可以结合运动频率与此时的正弦运动最大幅值来分析加速度的最大误差。

基于运动学分析获得的自由度空间与铰点空间的转换关系是一种精确的数学模型，运动学算法的解算误差可以忽略不计，因此可以利用运动学算法根据实验测得的各液压缸的位移、速度和加速度解算出平台实际位姿和实际加速度。

4.1 pz运动误差及耦合

根据零位线性化推导出的矩阵算法，系统运动位姿越大，偏差越大。但是对于正交布置的振动台，零位线性化理论sinx=x只用于对平台Rz,Ry,Rx自由度的解算。当平台进行px,py,pz单自由度平动时，平动方向上的液压缸的位移量没有误差，而转动自由度矩阵算法误差较大。

仿真表明，平动自由度最大解算误差为5×10-9m，该误差已经超出传感器的分辨率，对系统控制精度的影响可以忽略。但由矩阵算法导致的对其他自由度产生的自由度之间的耦合运动较明显。

实验给定pz自由度幅值为0.03 m，频率为0.5 Hz的正弦运动，采用矩阵控制算法。矩阵算法产生的rx耦合如图5所示，平台pz越大时，产生的rx耦合越大。

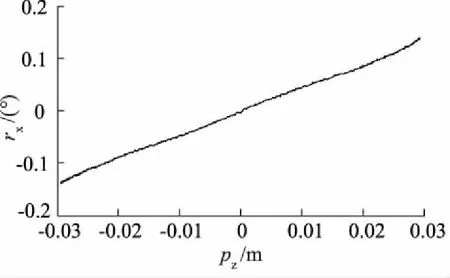
图5 矩阵算法下产生的耦合(pz自由度运动)

4.2 Rx运动误差及耦合

定义矩阵算法对平台位置的解算误差的计算公式为:

(14)

其中,qh为矩阵算法解算的平台位姿；qr为平台实际位姿。

实验给定Rx自由度幅值为6°，频率为0.5 Hz的正弦运动，矩阵算法对平台位置的解算误差与平台实际位置的关系如图6所示。当平台rx增加时，矩阵算法对平台位姿的解算误差明显增加。

定义平台正弦运动时，矩阵算法对平台加速度的解算误差计算公式如下：

其中,ah(ω)为振动频率为ω时矩阵算法解算的平台加速度；ar(ω)为振动频率为ω时平台实际加速度。

图6 矩阵算法解算误差(Rx自由度运动)

不同频率F下，进行多组Rx正弦实验，幅值为该频率下平台最大运动范围的50%，低频采用位置控制模式，三状态输入为平台位置信号；高频时采用加速度控制模式，三状态输入为平台加速度信号。其中10 Hz(加速度控制)平台加速度arx时域响应如图7所示。根据式(15)求取矩阵算法的误差，结果如图8所示。图中实线为仿真结果，是利用MATLAB构建的数学模型计算得到的理论误差；虚线为实验中矩阵算法得到的平台加速度误差。由图中结果可知，在低频运动时，受液压缸最大伸缩量限制，平台具有相同的运动范围，矩阵算法的加速解算误差最大约为1.2%，实验结果与仿真结果接近；当平台做中频或高频运动时，受液压缸最大速度或加速度限制，频率越高平台运动范围越小，矩阵算法的加速解算误差明显减小。考虑液压动力机构动力学特性差异、传感器误差等其他因素作用下，此时矩阵算法的解算误差要远高于仿真结果。因此在中高频运动时，矩阵算法的加速度解算误差对系统精度的影响很小，可以忽略不计。

图7 10 Hz时平台加速度arx时域响应

给定Rx自由度幅值为6°，频率为0.5 Hz的正弦运动，采用矩阵控制算法，产生的ry耦合如图9所示。由结果可知，当平台rx越大时，矩阵算法产生的ry耦合越大。

图8 矩阵算法的加速度解算误差(Rx自由度运动)

4.3 算法执行周期TET

算法的执行周期是实时控制系统设计的重要指标。由图6、图8可知，运动学分析有助于提高低频段的控制精度。对于高频信号，考虑液压动力机构的动态特性差异及传感器噪声等因素的影响，运动学分析的优势并不明显。图10给出了矩阵控制与运动学分析相结合的控制策略。该算法在传统的纯矩阵控制策略基础上，以位置正解替代原本的合成矩阵，以此提高低频段控制精度。对于速度及加速度，仍基于合成矩阵求取。