基于广义二次互相关的低信噪比信号时延估计

钱隆彦,陈卫松,肖梦迪

(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)

0 引言

时延估计在声源定位领域的研究及应用日益广泛。 在计算时延的方法中,基于到达时间差的定位方法因其计算量小、定位耗时少等特点,被广泛应用[1]。 早期计算时延算法主要是广义互相关算法[2-3],近些年二次相关算法和广义二次相关算法在时延计算中得到了应用[4-5]。 茅惠达等人基于传统广义互相关算法,利用加权函数增强了信号中信噪比(SNR)较高的频率,从而提高了时延估计精度,但在低SNR 情况下,抗噪声性能下降[6]。 唐娟等人将两路信号自相关和互相关的结果再做一次相关运算,得到二次相关函数,算法在高SNR 时增大了信号的相对值,降低了噪声的干扰,但在低SNR 环境下获取时延估计精度不高[7]。 朱超等人基于广义二次相关算法,将二次相关函数与加权函数相乘,并用希尔伯特算法锐化峰值,提高了时延准确度,但低SNR 情况下,峰值受噪声干扰大,峰值锐化不明显[8]。 本文提出一种基于广义二次相关的时延估计改进算法,在低SNR 情况下,抗噪声性能和正确率下降缓慢,提高了时延估计的精度与抗噪声性能。

1 广义二次相关时延估计算法

广义二次相关时延估计算法的流程如图1 所示。 先对接收信号1 做自相关运算,同时对两路接收信号做互相关运算,然后对自相关和互相关运算的结果再次做相关运算,得到二次相关函数[9],再把二次相关函数与广义加权函数相乘,得到广义二次相关函数,最后进行峰值检测,从而得到时延估计值[10-11]。

在没有混响,且相关噪声较弱的情况下,2 个麦克风接收到的信号可表示为：

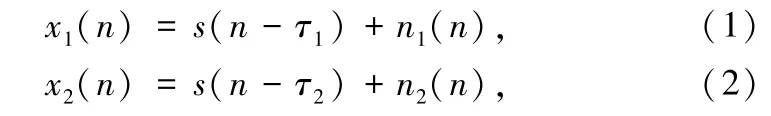
式中,s(n) 为接收到的声源信号,n1(n),n2(n) 为白噪声,τ1,τ2分别为信号从声源到达2 个麦克风的时间,信号到达2 个麦克风的时间延迟为τ12= τ1- τ2。

将两路信号的自相关和互相关函数做二次相关运算,得到二次相关函数,可以表示为：

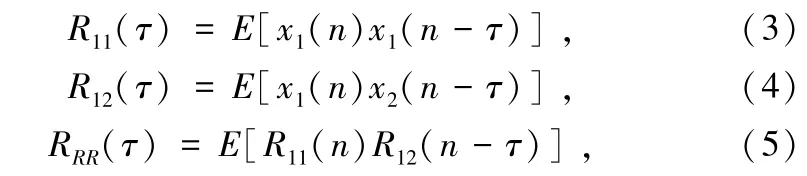
式中, R11(τ) 为自相关函数, R12(τ) 为互相关函数,RRR(τ) 为二次相关函数。

假设噪声和信号互不相关,将式(3)和式(4)代入式(5)可得：

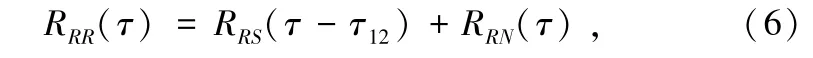
式中,RRS代表纯净信号做二次相关,RRN代表噪声做二次相关,由相关函数的性质可知,当τ = τ12时,RRR取最大值,τ12为2 个麦克风之间的时间延迟。

广义互相关法是将互相关函数变换到频域,然后对其互功率谱进行加权,抑制噪声对信号的影响,再反变换到时域,得到广义互相关函数。

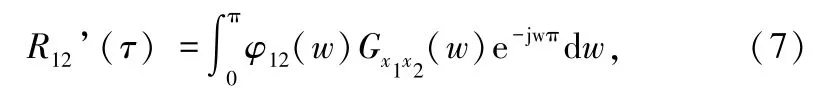
式中,Gx1x2(w) 为接收信号的互功率谱, φ12(w) 为加权函数。

本文所用的加权函数为SCOT(平滑相干加权函数)：

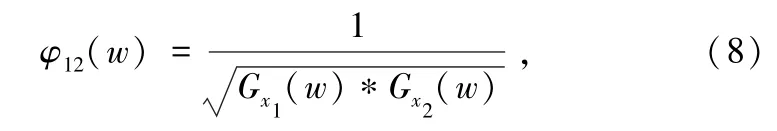
式中,Gx1(w),Gx2(w) 为两路信号的功率谱。 平滑相干方法首先利用平滑相干加权函数对信号功率谱进行白化处理,然后计算麦克风接收到的两路信号的互功率谱。 当SNR 较大的情况下,SCOT 方法不依赖声源信号的能量,可以有效克服信号的波动对时延估计的影响[12-13]。

2 改进的广义二次互相关时延算法

二次互相关在基本互相关基础上发展,在高SNR 情况下,信号强度大于噪声强度,二次相关运算增加了信号强度,所以在高SNR 情况下,二次互相关算法优越于基本互相关算法。 但是随着SNR降低,噪声强度大于信号强度,二次相关运算增加了噪声强度,因此在低SNR 情况下,二次互相关法进行时延估计的正确率下降。 在广义二次互相关算法的基础上,把二次互相关函数做指数运算,再乘以加权函数,最后把傅里叶逆变换得到的互相关函数做高次方运算,可以让峰值突出,再进行峰值检测,从而得到时延估计值。 其算法原理框图如图2 所示,虚框内为算法新增部分。

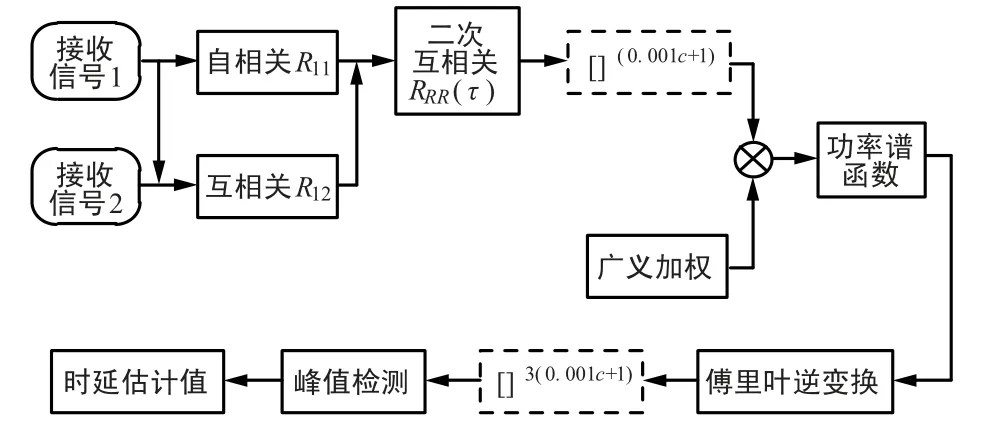
图2 广义二次互相关加权函数改进算法流程图Fig.2 Flow chart of improved algorithm of generalized quadratic cross correlation weighting function

图2 中右上角虚框内的公式可表示为：

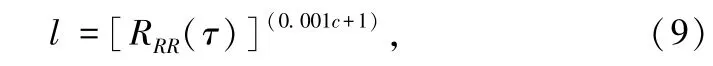
式中,l 为二次相关指数运算结果,c 为SNR。

图2 中右下角虚框内的公式可表示为：

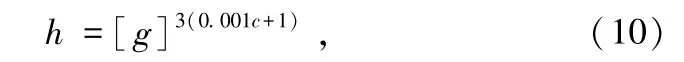
式中,h 为傅里叶逆变换指数运算结果,g 为傅里叶逆变换后的相关函数。 为了便于分析式(9)的函数规律,取二次互相关值RRR为2.0,2.2,2.4,得到一簇输出量l 随SNR 变化的曲线如图3 所示。

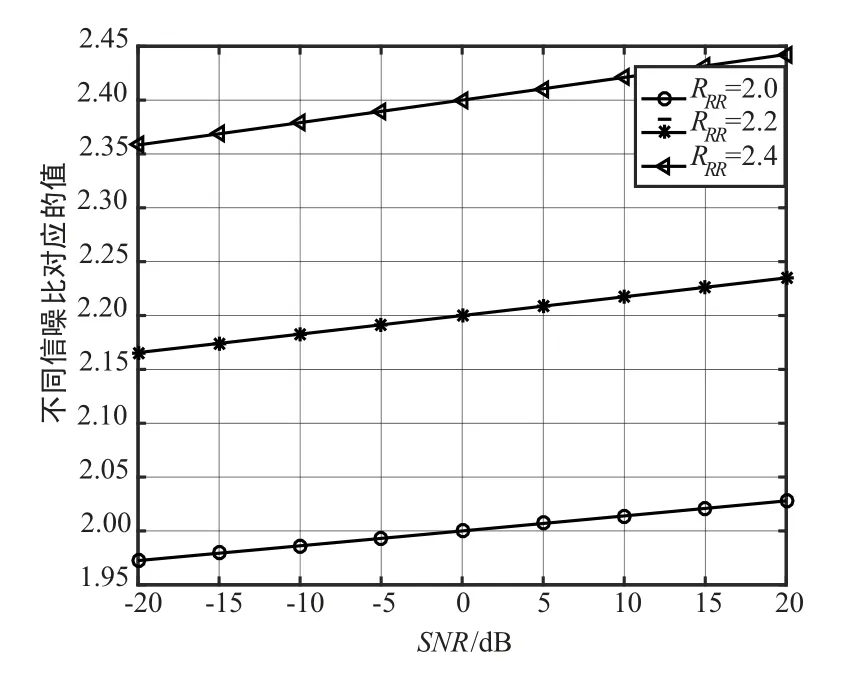
图3 式(9)中l 值随SNR 变化关系Fig.3 Relationship between L value and SNR in equation (9)

由图3 可见,在SNR=0 时,指数为1,运算结果为二次相关函数本身;当SNR＜0 时,指数小于1,二次相关函数类比于开根号运算,此运算可以随SNR变化压缩噪声和信号的幅度。 虽然降低了噪声强度,但是噪声和信号的压缩比例是一样的,即此时噪声强度还是高于信号强度,由于噪声随机,可以通过对信号分帧,并对每帧信号进行多次时延计算求平均值,降低随机噪声对计算结果的影响,从而增强主峰值;当SNR＞0 时,二次相关函数可类比于平方运算,原理与二次相关函数相同。 通过式(9)的运算,函数峰值钝化,式(10)的高次方运算可增大主峰和次峰的相对值,起到锐化峰值的作用。

为了验证改进算法的时延估计性能,对改进算法进行仿真实验。 仿真环境不考虑混响的影响。 信号源为NOIZEUS 实验室纯净语音库里编号为fdnc0.9 的测试语音,采样频率为8 kHz,每帧采样点为2 000,延时点数为20。 信号中添加平稳高斯白噪声。 假设信号与噪声、噪声与噪声都是相互独立的,当SNR=5 dB 时,广义二次相关算法和改进的广义二次相关算法结果如图4 所示;当SNR=-5 dB时,广义二次相关算法和改进的广义二次相关算法结果如图5 所示。

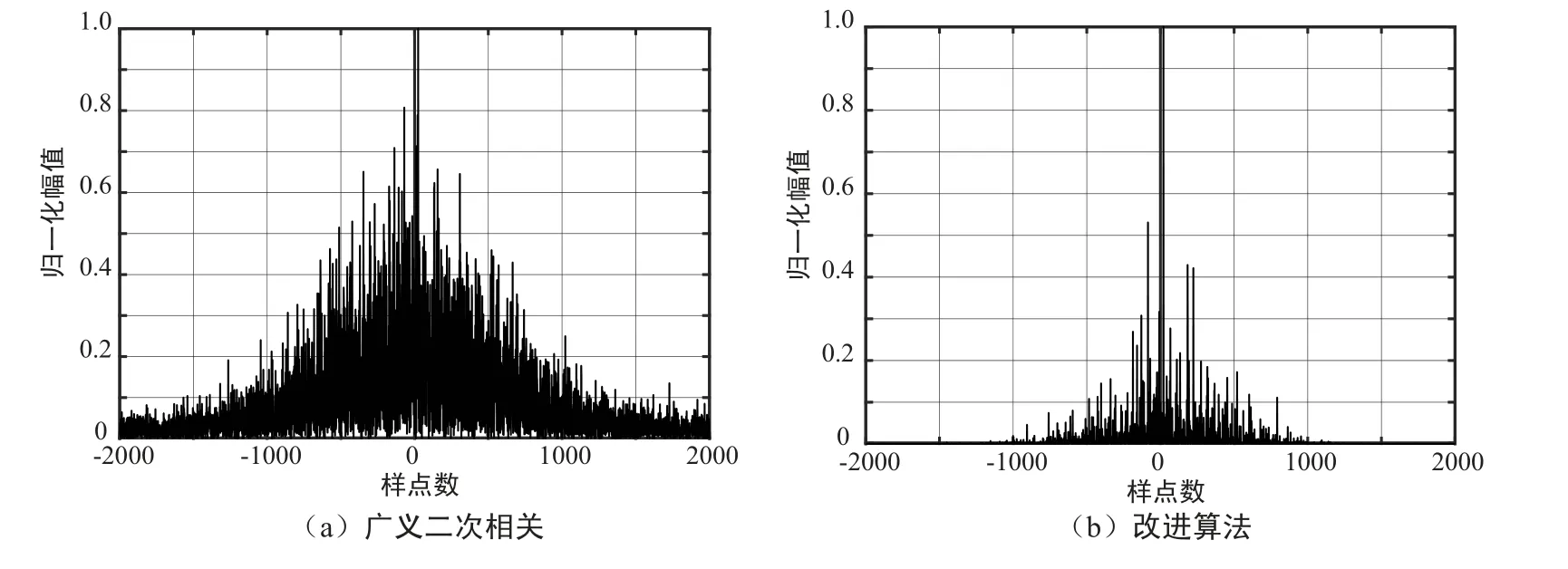
图4 SNR=5 dB 时广义二次相关和改进算法时延估计比较Fig.4 Comparison of generalized quadratic correlation and improved algorithm for time delay estimation when SNR=5 dB

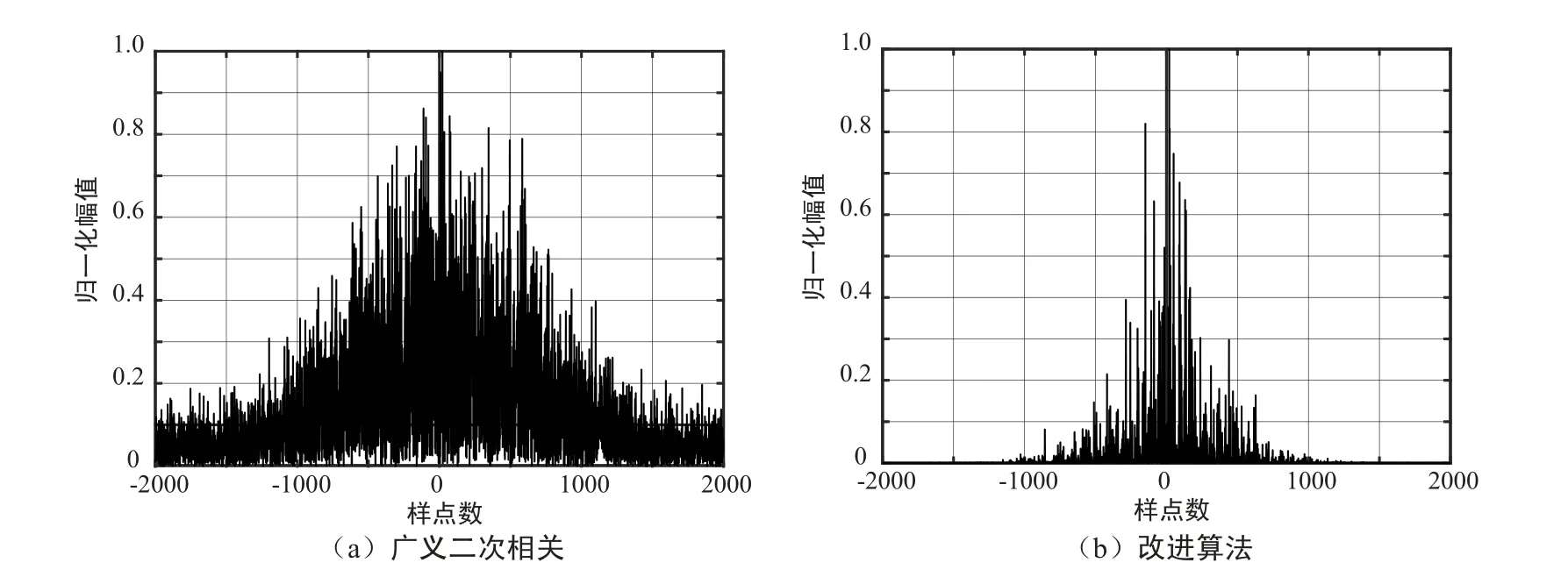
图5 SNR=-5 dB 时广义二次相关和改进算法时延估计比较Fig.5 Comparison of generalized quadratic correlation and improved algorithm for time delay estimation when SNR=-5 dB

从图4 可以看出,在SNR=5 dB 时,2 种算法峰值突出,都可以得到准确的时延值,但改进的广义二次相关算法得到的最大值和其他次峰值相差更大。

从图5 可以看出,在SNR=-5 dB 时,广义二次相关法的相关函数峰值受周期信号影响较大,峰值不明显,而改进算法具有锐化相关函数峰值的作用,信号相关函数的峰值尖锐,时延估计效果更好。

为进一步验证所提出时延估计算法的有效性,对二次相关、广义二次相关、改进的广义二次相关算法的均方根误差(RMSE)和时延正确率进行仿真实验。 首先比较SNR 在-20 ～20 dB 时不同算法的RMSE。 信号源仍然选用NOIZEUS 实验室纯净语音库里编号为fdnc0. 9 的测试语音,采样频率为8 kHz,每帧采样点为2 000,延时点数为20,均方根误差定义为：

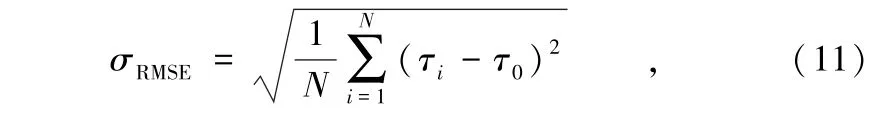
式中,τ0为真实时延估计值, τi为第i 个时延估计值,N 为时延估计总数,对3 种算法分别进行N =100 次仿真,仿真结果如图6 所示。

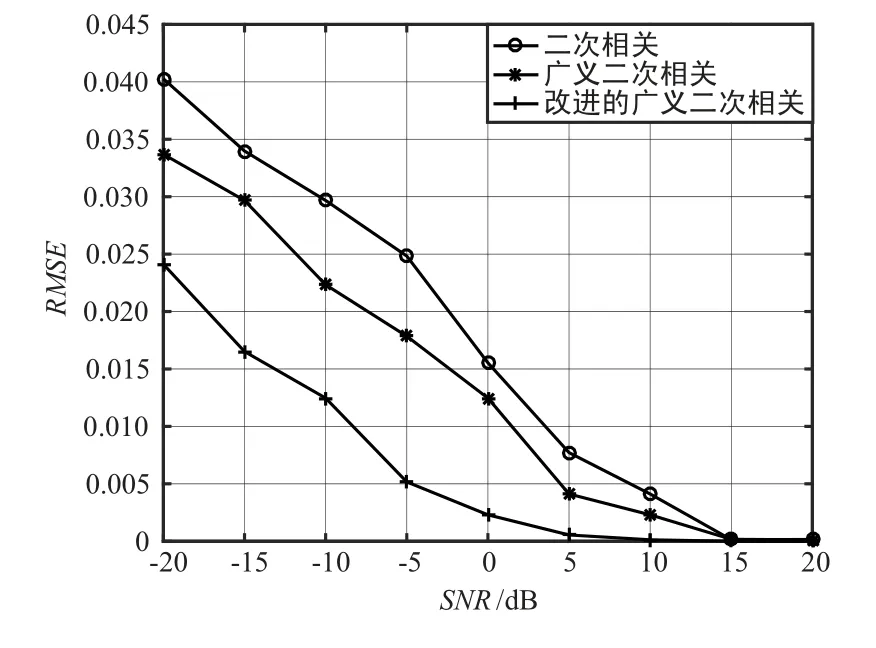
图6 3 种算法的RMSE 随SNR 变化比较Fig.6 Comparison of RMSE changes with SNR of three algorithms

从图6 可知,随着SNR 的降低,3 种算法的均方根误差RMSE 都会变大。 在SNR 在15 ～20 dB 时,3 种算法的估计性能差别不大;在5～15 dB 时,二次相关算法、广义二次相关算法的RMSE 会随着SNR的降低而变大,而改进的算法几乎没有变化,RMSE值接近于零;随着SNR 继续降低,在-20 ～5 dB 时,二次相关算法、广义二次相关算法的RMSE 会随着SNR 的降低而迅速变大,改进算法的RMSE 值变化较为缓慢,表明其仍具有较好的时延估计性能。 以上结果表明,在SNR 较低时,改进算法表现出比另外2 种算法更好的时延估计误差。

其次,比较3 种算法的时延正确率。 信号源与上述均方根误差计算所选信号源相同。 在不同的SNR 下,每帧信号做100 次仿真,得出峰值对应的延迟点数,根据峰值对应的延迟点数,取平均值。 因为加入的是随机噪声,通过对峰值对应的延迟点数取平均值,可以降低随机噪声的干扰[14]。 由于选取的信号源采样率不高,对时延估计的精度有一定影响,因此误差率设定为20%,即时延估计值和时延真实值之间偏离4 个采样点以内时,认为该估计值在误差允许范围内。 时延估计正确率如图7 所示。

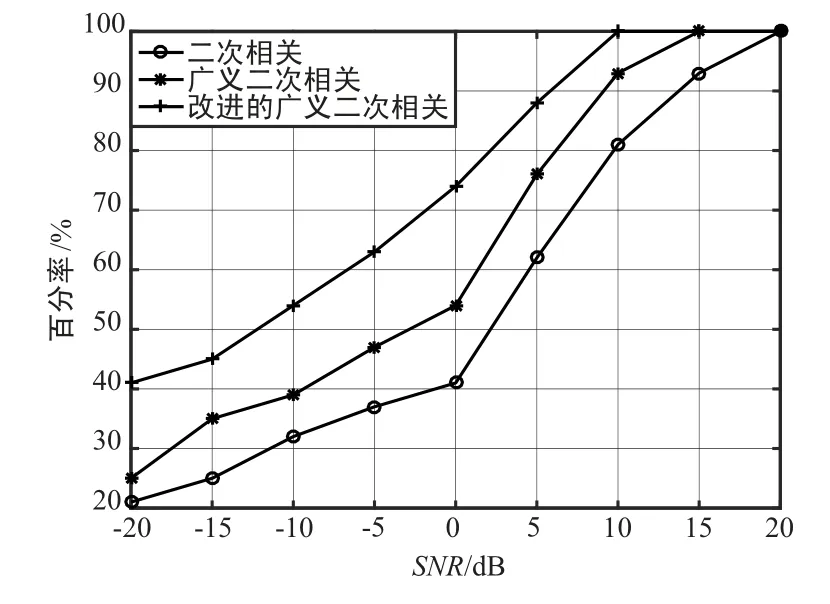
图7 3 种算法的实验估计正确率随SNR 变化比较Fig.7 Comparison of the experimental estimation accuracy of the three algorithms with the change of SNR

从图7 可以看出,随着SNR 的降低,3 种算法的时延估计正确率都下降。 SNR 在10 dB 以上时,二次相关算法、广义二次相关算法的时延估计正确率开始降低,而改进算法的时延正确率仍达到100%;SNR 在-5～10 dB 时,二次相关算法、广义二次相关算法的时延估计正确率迅速降低,而改进算法的时延估计正确率下降缓慢,正确率在70%左右;在-20～-5 dB 时,二次相关算法、广义二次相关算法的时延估计正确率显著下降,而改进算法仍具有较高的正确率,正确率比前者提高了近20%。 SNR 在-5～10 dB 时,不论是均方根误差还是正确率,改进的广义二次相关算法均比另外2 种算法有一定优势。

4 结束语

针对广义二次相关时延估计算法在低SNR 情况下,算法性能和正确率下降的问题,本文提出了一种改进的广义二次相关算法。 通过对相关函数进行指数运算,削弱噪声的干扰,再通过对傅里叶逆变换的结果进行高次方运算,锐化二次相关计算结果的峰值,从而达到了提高时延计算正确率的目的。 仿真结果表明,在0～10 dB 的SNR 情况下,改进算法的RMSE 明显优于另外2 种算法,在时延正确率上,改进算法的正确率提高了近20%;在更低SNR 情况下,改进算法也表现出一定的优势。 因此改进算法在时延计算过程中,对于低SNR 信号,抗噪声性能有明显改善。