环境规制可以“双赢”吗？——中国工业行业细分视角下的强“波特假说”研究

鞠可一，周得瑾，吴君民

（江苏科技大学 经济与管理学院，江苏 镇江 212003）

改革开放四十年来，中国经济依靠“粗放型”发展取得了瞩目的成绩，也造成了严重的资源与环境问题。《全球环境绩效指数评估报告（2018）》[1]显示，2017年中国环境绩效得分只有50.74分，在全球180个国家和地区中排名第120位。2018年10月，联合国政府间气候变化专门委员会（IPCC）通过了《IPCC全球升温1.5℃特别报告（2018）》[2]，报告指出，到2030年，全球CO2排放量要比2010年的水平下降大约45%。这意味着，中国作为全球能耗和排污“大国”，迫切需要在能源和环境方面提出更加切实高效的规制手段。因此，依据各领域特点，有针对性地制定合理且高效的环境规制手段，推动绿色全要素生产率（Green Total Factor Productivity，GTFP）的持续改善，实现环境与经济发展“双赢”具有重要的现实价值。

一、文献综述

学术界对于环境规制的影响效应主要集中于两个方面，较早是以新古典经济学派为代表的“遵循成本”效应，认为环境规制将导致企业产生额外成本，降低企业竞争力[3-4]。Porter[5]提出“创新补偿”效应，认为严格且合理的环境规制可以激发企业创新，从而能够部分甚至完全抵消企业的“遵循成本”[6-7]，该理论的提出引起了众多学者的关注。1997年，Jaffe和Palmer[8]在Porter的基础上提出：环境规制不仅能够激发企业创新，还能够提高企业竞争力，该理论被定义为强“波特假说”。

现有关于强“波特假说”的研究已有许多文献，考虑到GTFP作为能源效率指标具有综合多维度的特征，国内外学者多选取GTFP表征企业竞争力，以此研究环境规制对GTFP的作用[9][10]758-766。较早主要是检验环境规制对生产率是否有积极影响，但始终没有得到一致的定论[11-12]。许多学者利用计量模型检验环境规制对GTFP的影响，得出环境规制对GTFP影响为负向[13][14]126-127或者正向[15][16]180-182；也有学者认为，环境规制与生产率没有必然联系[17-18]。随着研究的深入，有学者分别从区域异质性的角度[19-20]和环境规制差异性的角度来进行验证[21]；原毅军和谢荣辉[22]对强“波特假说”进行验证。近年来，中国工业快速发展导致能源和环境问题日益突出，更多的学者开始将强“波特假说”纳入行业的研究范畴，目前，已有学者开始关注高污染、高耗能行业的强“波特假说”[23-25]；但很少有学者对污染同样很高但还未引起国家重视的中度污染行业进行研究。中国如今取得的环保成绩主要依赖于“低果先摘（picking the low-hanging fruits）”式的减排政策，当这些“低果”将被摘完的时候应该对中间污染行业的环境问题引起足够重视[26]。刘传江和赵晓梦[27]7-8提出中碳密集型产业成为“被遗忘的角落”。

由此可以看出，已有文献已从多种角度对强“波特假说”进行了探讨，但针对行业异质性研究的题材还不够深入，均将注意力放在重度污染行业研究上面，往往忽视了中间污染行业的重要意义，并且对行业进行划分时依据单一，不能准确反映各类型行业污染特点。鉴于此，本文基于强“波特假说”的检验，建立动态模型，分析环境规制强度对不同行业类型GTFP的差异性影响，结合当前环境规制作用效果，理清环境规制与行业发展之间的关系，为政府制定最优环境政策组合提供更加丰富的参考。相较于以往的研究，本文在行业分类过程中参照《中华人民共和国环境保护税法》（以下简称《环保税法》）标准，规避了不同污染物间不可相加性导致的计算失真问题，综合考虑排污规模和污染强度两个层面，使结果更有参考意义；通过SYSGMM模型对强“波特假说”进行检验，结合门限回归模型对比门槛值和当前值，得到环境规制对GTFP的影响情况和影响现状，从而找到最优规制政策组合；从中间污染行业入手，通过检验验证中间污染行业减排空间巨大，为接下来环境政策提供理论依据。

二、基于排污规模及污染强度的行业分类

（一）行业划分及说明

依据国家统计局公布的《国民经济行业分类（2017）》，中国工业被划分为41个行业。由于2010年国家对工业行业进行重大调整，为确保数据的连续性和有效性，本文剔除了金属制品机械和设备修理业、废弃资源综合利用业（2010年以前为废旧材料回收加工业）、其他制造业和开采辅助活动等四个类型；合并2010年以前（含2010年）的橡胶制品业和塑料制品业为橡胶和塑料制品业；将2010年以前（含2010年）的交通运输设备制造业，按照2010年以后的汽车制造业与铁路船舶航空航天和其他运输设备制造业的占比进行拆分，最终确定37个行业。

（二）行业分类方法

在对行业进行划分方面常见的有三种方法：一是从单一污染物入手[28]；二是根据污染物排放强度划分[29]；三是使用减污成本和支出[30]62-68。显然，由于选择指标代表性不强、污染物的不可相加性以及行业性质不同，这些方法对行业进行划分均不能很好地表达行业间的污染状况。因此，本文从排污规模和污染强度两个方面建立污染密集指数进行划分。

1.主要污染物排放量（E）。参考环境监测的主要指标，考虑数据可得性，确定化学需氧量（COD）和氨氮排放量为水污染物排放指标，二氧化硫（SO2）、烟尘、粉尘排放量为气体污染物排放指标，一般工业固体废物和危险废物产量为固体废物排放指标。

2.污染贡献量（C）①本文“污染贡献”指的是对污染物排放征收的税费额，是从纳税角度对污染物排放进行的统计，与传统意义上的“污染损失”虽然表述不同，但表示的是一个问题的两个方面。。指依据税率标准计算不同污染物所需税费，最后得出所有污染物的总税费，税费越高表明其排污情况越严重，在排污行为中的“贡献”越大。参考叶金珍和安虎森[31]提出环保税中碳税具有异质性处理效应的结论，选用《环保税法》的相关指标，将主要污染物排放量折算为污染贡献量

其中，Ci表示第i行业污染物贡献量；Eij表示第i行业第j污染物排放量；Tj为j污染物的税额②由于《中华人民共和国环境保护税法》中税额为区间，本文选取中值进行计算。；PEj为j污染物的污染当量值。由于固体废物不涉及当量计算，因此进行单独计算，具体如表1所示。

表1 污染贡献量计算相关参数

3.排污规模（CR）。表示各行业污染贡献量占全工业行业总贡献的比重①本文因选取37个行业，故工业部门污染贡献总量为37个行业贡献量之和。。表达式为

4.污染强度（E）。第i行业的污染强度为第i行业污染贡献量与第i行业经济产出的比值。由于经济产出数据无法收集，本文考虑用与其数值相等的工业销售产值②工业销售产值平减为以2003年不变价格。Vi代替，具体公式为

5.污染密集指数（I）。利用线性标准化后的污染贡献率和污染强度计算几何平均值[27]2-3

I越大，表明该行业污染状况越严重；I越小，表明该行业污染状况越乐观（如图1所示）。利用K-means聚类分析法对各类行业进行分类，Ii≥0.113属于重度污染型行业；0.010≤Ii≤0.081，属于中度污染型行业；Ii≤0.009，属于轻度污染型行业。其中，气泡越大表示污染密集指数越大③通过与Shen等[16]175-176的分类结果进行对比，发现其文中三类行业数按重、中、轻度污染行业分别为9、16、11（本文结论为12、14、11），各类别中重合率超过80%，不一致的原因可能是其选用了2000—2016年行业数据，进而产生了一定的差异。，污染密集指数表示2003—2015年累计值得分。

三、三类污染型行业GTFP测算

（一）超效率混合距离函数

EBM（Epsilon-Based Measure）模型是一种包含径向和非径向模型特点的混合模型[32]，该模型既可以有效反映投入目标值与投入实值的径向比例，又能反映各投入产出变量非径向部分的差异，能够更加真实地反映评价单元的相对效率[33]。为避免EBM模型结果出现多个DMU被评价为有效的情况，本文结合超效率模型与EBM模型，建立Super-EBM模型计算绿色技术效率[34]，基于产出导向Super-EBM模型规划式为

其中，γ*表示最优效率值，满足表示各项产出指标的相对重要程度；ε+是一个关键参数，取值范围为[0，1]，表示在效率值的计算中非径向部分的重要程度，取0相当于径向模型，取1相当于SBM模型；x和y分别是投入矩阵和产出矩阵；s+是产出指标的松弛变量；λ表示参考决策单元的相对重要程度；φ为变量。

假设测算 n 个决策单元（DMU）的效率值，记为 DMUj（j=1，2，…，n）；当前要测算的 DMU 记为 DMUk；每个 DMU 包含 m 种投入，记为 xi（i=1，2，…，m）；q 种产出（r=1，2，…，q），记为 yr（r=1，2，…，q）。

全局参比Malmquist指数是Pastor和Lovell[35]提出的一种Malmquist指数计算方法。由于其具有传递性，同时可以避免VRS无可行解问题，构建包含非期望产出的Malmquist-Luenberger指数（GML指数），测算基于含非期望产出EBM模型的GTFP[36]。GML指数表达式为

其中，bt、bt+1表示决策单元t和t+1期的非期望产出。方向性距离函数如下

（二）GTFP测算指标选择

选取2003—2015年37个工业行业面板数据，各类投入产出数据来源于《中国统计年鉴》《中国工业统计年鉴》《中国能源统计年鉴》《中国经济普查年鉴》和国家统计局网站。

1.资本投入。资本投入借鉴董敏杰等[37]的方法，以固定资产净值，即固定资产原值与累计折旧的差额表示资本投入①固定资产净值平减为以2003年不变价格。。

2.劳动投入。以各工业行业历年全部从业人员年平均人数衡量。由于2012年全部从业人员平均人数丢失，利用线性插值法补充。

3.能源投入。以各工业行业历年能源消费总量衡量。

4.期望产出。选取工业销售产值为期望产出，平减为以2003年为基期。

5.非期望产出。本文选取COD、氨氮、SO2、CO2、一般固体废弃物和危险废物为非期望产出。

（三）GTFP测算结果与分析

通过MaxDEA7-Ultra测算GML指数，在测算过程中需要相邻两年的变化率，会损失一个自由度，得到2004—2015年的GML指数。由于GML指数表征GTFP的增长率，采用邱斌等[38]的方法对GTFP进行计算，假设2004年GTFP为1.000，则2005年GTFP为2004年指数乘以2005年GML指数，以此求得2004—2015年GTFP。具体结果如图2所示。

从图2可看出，全行业GTFP平均值从2004年的1.024增长到2015年的1.405，2005—2008年和 2010—2012年有两个快速上升阶段，可能是因为“十一五”及“十二五”开局阶段，各环保政策的制定和推动有效地控制了污染物的排放。分行业类型看，一方面，首先是重度污染型行业GTFP增幅最快，是唯一高于全行业GTFP的类型，其次是中度污染型行业，最后是轻度污染型行业。另一方面，从2005年开始，重度污染型行业GTFP呈现出稳定增长的态势，而中度和轻度污染型行业，特别是中度污染型行业GTFP增长缓慢。由此可以推断，在政府花费巨大精力对重度污染型行业GTFP的关注下，重度污染型行业的GTFP已经得到很大的提升。因此，提高中度和轻度污染型行业GTFP是目前提高全行业GTFP的关键。

四、基于GTFP的强“波特假说”检验

（一）环境规制强度测算

用工业行业治理废水、废气的运行费用与对应工业销售产值之比作为环境规制强度 （ER）的测算值（Lanoie等[14]121-128）。ER越大，表明环境规制强度越大。

其中，ER表示行业的环境规制强度；OC为行业的废水、废气治理运行费用 （数据来源：《中国环境统计年鉴》）；V为行业的工业销售产值；r分别取重度、中度和轻度污染型行业。

利用三类污染型行业2003—2015年环境规制强度值，绘制如图3所示，重度污染型行业受国家政策调控的灵敏度高，由于20世纪90年代中期开始的国有企业改革对行业进行重组，2003—2005年重度污染型工业行业的环境规制强度出现了短暂减退，直至2011年，在国家出台了一系列相关环境保护条例的基础上，其环境规制强度快速提升。中度和轻度污染型行业环境规制强度出现逐年下降趋势，且中度污染型行业环境规制强度的下降幅度更为明显。总体而言，自2003年以来，重度污染型行业环境规制强度远高于中度和轻度污染型行业，中度污染型行业次之，轻度污染型行业最低，这一结论表明，重度污染型行业一直是工业行业污染治理的重点对象，而中度和轻度污染型工业行业的环境规制强度仍有提高的空间。

（二）实证检验

本文主要研究环境规制对GTFP的影响，选取环境规制及环境规制二次项为解释变量，如果二次项系数与一次项系数相同，则表明环境规制对GTFP影响为线性，相反则为非线性。考虑到环境规制对GTFP的影响可能存在滞后性，将GTFP的滞后期作为解释变量[39-40]，构建如下模型

其中，GTFPi，t为第i个行业第t年的 GTFP；GTFPi，t-1表示滞后一期 GTFP；ERi，t为环境规制强度为环境规制强度二次项；Xi，t为影响行业 GTFP 的其他因素；Vi，t表示个体效应；εi，t为随机扰动项。控制变量 Xi，t可表示为

其中，Sizei，t为行业相对规模；OSi，t为所有制结构；RCPi，t为毛利率，表示行业盈利能力；LPi，t劳动生产率；EPi，t为能源生产效率。各变量描述性统计如表2所示。

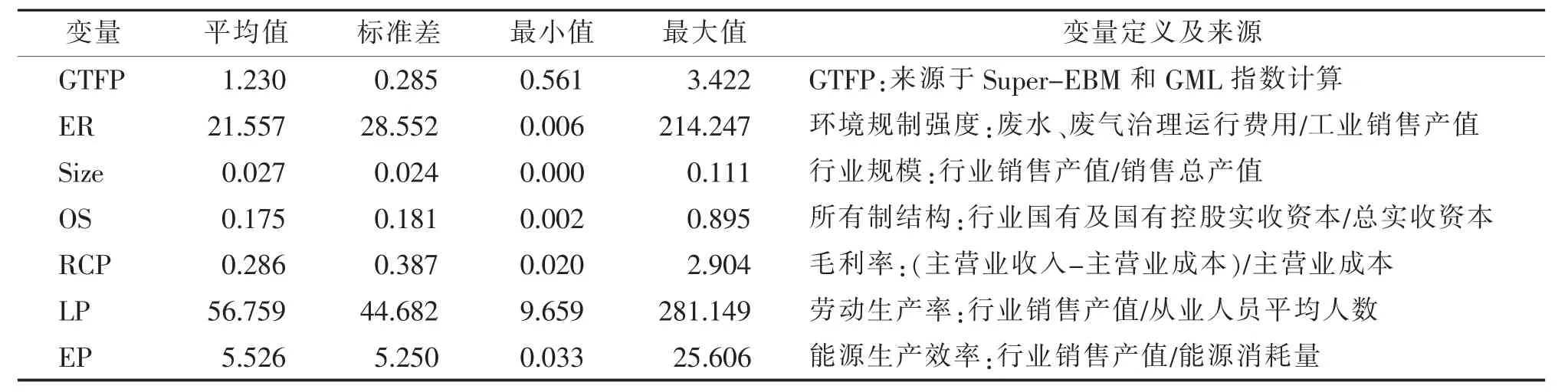
表2 各变量描述性统计分析

（三）环境规制对GTFP的影响检验

通过StataSE 15采用系统广义矩估计（SYSGMM）对式（9）和式（10）进行回归分析。在回归分析之前，首先进行相关检验，如表3所示，AR（2）检验与P值均大于0.05，拒绝原假设，说明动态面板不存在二阶自相关。Hansen检验与P值均大于0.05，说明选取的工具变量有效。且整体均通过F检验。为测试SYSGMM的回归效果及稳健性，本文选取静态面板模型与SYSGMM模型进行对比分析。对静态面板模型进行Hausman检验，当P值大于0.1时，选用随机效应模型；若P值小于0.1时，选取固定效应模型。

由表3可知，全行业、中度和轻度污染型行业环境规制一次项（ER）系数为负，二次项（ER2）系数为正，说明环境规制与GTFP呈“U形”关系，即随着环境规制强度的提高，GTFP呈现先降低后升高的趋势，这与殷宝庆[30]62-68对制造业整体回归的结果一致，较之殷宝庆的研究，本文在对象上考虑更加全面，且分类更加细化。重度污染型行业环境规制强度与GTFP则呈“倒U形”关系，即随着环境规制强度的提高，GTFP呈现先升高后降低的趋势，这与Wang和Shen[10]758-766对污染型行业的研究结论一致，本文是从污染排放角度对行业进行分类，且切入点为中间行业。因此，无论全行业还是三种污染型行业，环境规制在一定范围内对GTFP均存在促进作用，从而验证了强“波特假说”。通过对比静态模型估计结果，发现两种模型趋势一致，且利用SYSGMM测算的结果显著性均优于固定效应回归结果，验证了该模型的稳健性。

表3 模型回归结果

为分析目前环境规制强度所处位置，利用门限回归[41]得到各行业环境规制门槛值，参考图形特点，绘制环境规制对GTFP影响趋势图，如表4所示。从门槛值来看，全行业门槛值为22.360，重度、中度和轻度污染型行业分别为35.319、15.465和1.397，不同污染型工业行业的门槛值差异性较大。要达到环境规制的“双赢”，应使环境规制处于一定强度，且保证GTFP可以持续提升。因此，对比环境规制当前值发现，全行业环境规制强度处于 “U形”曲线的上行阶段，即增强环境规制将提高GTFP，全行业环境规制强度当前值为23.232，刚刚跨过门槛值，继续增加环境规制强度将有利于GTFP的提升。从各类型来看，重度污染型行业当前值达到53.868已经高出门槛值0.53个百分点，且处于下行阶段，说明该类型环境规制强度过大，需要适当放宽以接近拐点。中度污染型行业当前值7.784只达到门槛值的一半，表明中度污染型行业环境规制强度还较弱，未能跨过拐点进入上升阶段，应逐步加大环境规制对中度污染型行业的治理力度。而轻度污染型环境规制当前值2.097已经达到门槛值的1.5倍，说明轻度污染型环境规制强度较其体量已经较强。

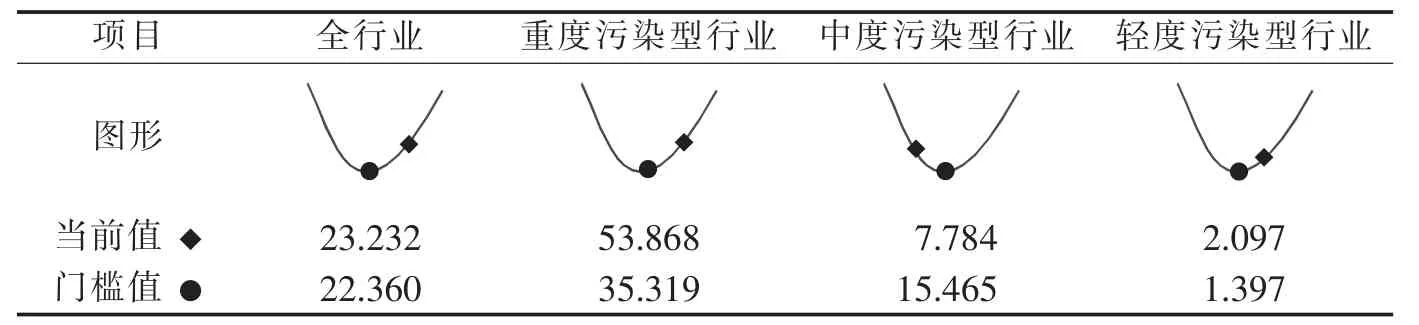
表4 工业行业环境规制门槛值与当前值对比

五、结论与建议

环境规制作为国家节约资源、保护环境的有效手段，面对当前严峻的环境问题和经济形势，作用尤为突出。特别是“低果先摘”政策无法满足目前的发展需求时，如何制定更加高效的环境规制政策，实现环境和经济的“双赢”，具有重要的现实意义。本文通过测算三类污染行业GTFP，建立SYSGMM模型检验了环境规制对GTFP的影响，得出如下结论：（1）环境规制强度由强到弱依次是：重度、中度和轻度污染型行业；（2）强“波特假说”表现出明显的行业异质性特点，重度污染型行业环境规制强度与GTFP之间呈“倒U形”关系，中度和轻度污染型行业环境规制强度与GTFP间呈“U形”；（3）当前重度污染型行业环境规制强度过高，中度污染型行业还未跨过拐点，有巨大的提升空间，轻度污染型行业已经处于相对合理区间。

针对该结论，本文提出政策建议如下：

1.转移规制重心到中间污染行业。中国之前所采取的“粗放式”环境规制主要针对的是高污染、高耗能的重度污染型行业，这种环境政策的确取得了一定成果。但重度污染型行业环境规制已经趋于饱和，污染问题同样严重的中度污染型行业环境规制还较弱，成长空间巨大，应当成为打破环境规制瓶颈的关键力量，以达成环境保护和经济发展的“双赢”。

2.对于重度和轻度污染型行业，应平稳转型，逐步优化产能效率。目前国内重度污染型行业环境规制强度已经过高，轻度污染型行业也高于门槛值，如果继续提高环境规制力度，将导致部分中小企业环境治理成本过高，不利于GTFP的全面提升。并且随着经济形势变化，各行业盈利空间减少，着力于长期目标规制，有的放矢，淘汰落后产能，在适度减小或者保持现有环境规制强度的情况下对重度和轻度污染型行业进行针对性调整，重要且必要。

3.充分考虑强“波特假说”存在行业异质性的特点，结合不同类型行业特点，制定最优环境规制组合。根据工业行业的整体情况，“一刀切”式地制定环境规制策略不仅可能削弱企业“创新补偿”的意愿，而且极易导致规制失效，无法达到环境与经济的“双赢”目标。鉴于此，根据三种类型工业行业的不同特点，对症下药，制定符合不同行业类型发展的环境规制组合，最大化环境规制效益，从而最大程度地实现环境保护与经济发展的“双赢”。