基于线谱幅值起伏的目标被动定位技术研究

魏德凯 朱代柱 郭浩泉

（上海船舶电子设备研究所，上海，201108）

近年来，随着各国减震降噪技术和机械推进技术的不断进步，水下目标辐射噪声级呈逐年降低趋势，这意味着对目标的定位变得越来越困难。考虑到水下目标诸如鱼雷、潜艇对水面舰艇和海域控制的巨大威胁性，低信噪比目标的被动定位技术被各国重视起来并逐年加大人力物力的投入。

被动定位以其较好的隐蔽性和抗干扰能力，一直是声呐致力研究的课题。经典的被动测距方法主要有三子阵法、聚焦波束形成方法、目标运动分析及匹配场处理等。三子阵法和聚焦波束形成方法利用了波前曲率仅适用于近程；目标运动分析方法作用距离较远，但需要较长的积分时间，且估距结果有一定的发散概率；匹配场处理因计算量较大以及对环境参数比较敏感而影响工程使用。近些年，基于波导不变量的被动定位技术因良好的定位性能而广受关注，但对干涉条纹的自动提取还存在一定的困难[1-2]。

本文提出的一种基于线谱幅值起伏的目标被动定位方法，在宽带检测失效、自相关无法估计出时延的情况下，利用目标辐射噪声中线谱的幅值与多途时延的关系，对时延进行估计，在假定目标深度的情况下可以利用单水听器实现对目标距离的估计，使用双水听器或基阵可以实现对目标距离和深度的三维定位。

1 原理

1.1 多途方法距离估计

图1中，设两水听器r1、r2的深度分别为H1和H2，水平距离L，目标深度为H3，与水听器r2的水平距离为R。以一个水听器r2为例，仅考虑直达声和一次海面反射声传播路径，就可以建立起目标水平距离R和直达声与海面反射声之间的时延差τ2之间的函数关系[3-5]。

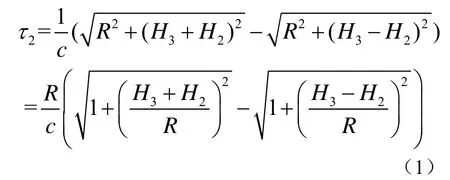
式中，c为水中声速，因为R>>H1+H2，所以可化简为

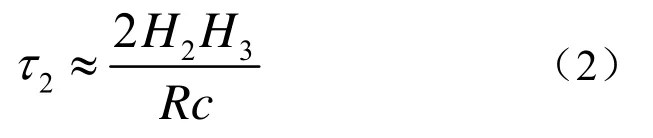
同理可得

此时可得到水平距离的估计公式

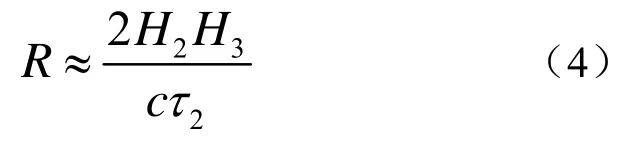
同理，对水听器r1可得

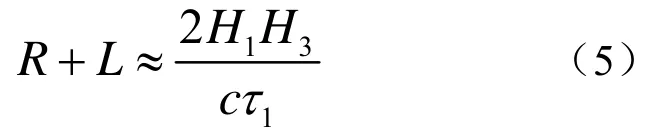
若测得τ1和τ2，则可估计出目标距离R和深度H3。

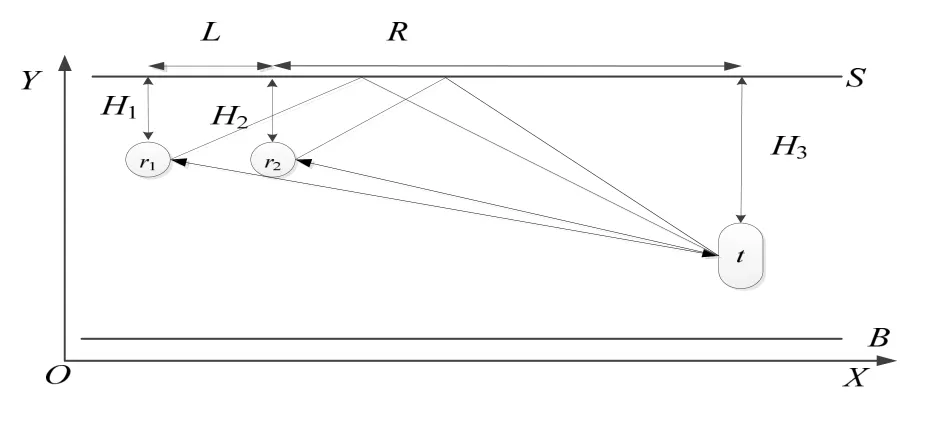
图1 浅海多途传播示意图

1.2 线谱幅值起伏时延估计

在目标信噪比很低时，宽带相关不可用，但此时线谱的信噪比要高于背景噪声，可以使用线谱的幅值起伏来估计时延τ2。设水听器接收端的信号为

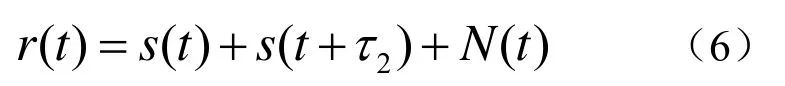
设其中的线谱分量为

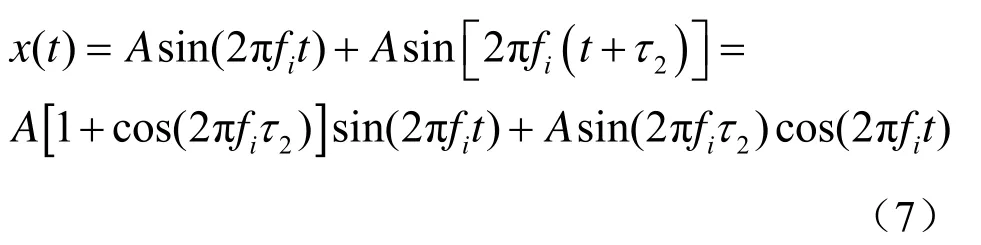
式中，fi为某一单频信号的频率，A为其幅值。对式（7）求FFT可以求得单频线谱幅值的平方为

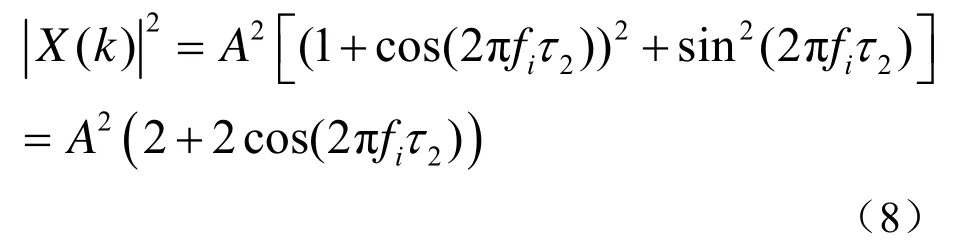
它是一个与时延有关的量，最大值为

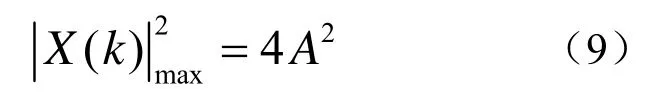
通过式（9）可以求出A，然后代入式（8）求出时延τ2为

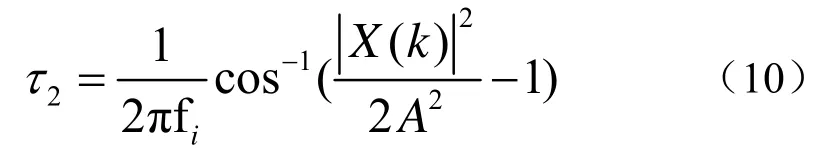
计算步骤：

（1）在较远距离上，时延非常小，用一段数据（40 s）统计测量结果，估计出初始时刻的线谱幅值平方最大值

（3）最后将步骤（2）估计结果A2(k+1)与观测得到的线谱幅值平方按照式（10）估计出多途时延值。

1.3 多线谱幅值起伏时延估计

当目标辐射信号中含有多根线谱时，各线谱虽然频率位置和幅值各不相同，但同一时刻不同fi的时延是相等的，用不同fi可估计出多个时延值，然后对多个时延求平均得到更加平滑的时延曲线，最终求得目标水平距离。仍然以r2接收信号为例，此时接收信号中的线谱分量为

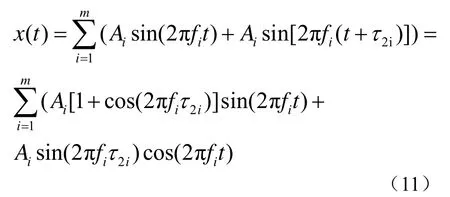
式中，m为线谱的的根数，对式（11）求FFT得到每一根线谱幅值的平方为

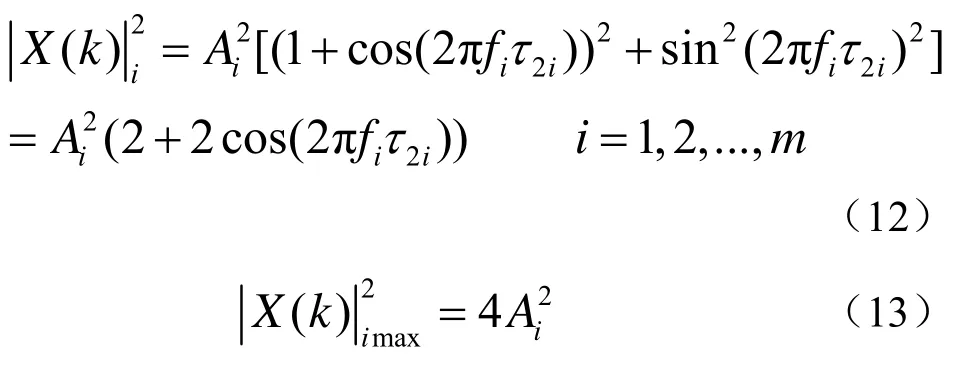
同样由式（13）估计出每一根线谱的幅值Ai，然后估计出各自的时延：

按照单线谱估计距离的步骤，对多线谱估计出的多个时延值求平均，将平均后的时延带入式（2）估计出水平距离。

1.4 目标距离与深度估计

利用单水听器估计时，需要先假设目标深度H3才能实现对目标水平距离R的估计。使用双水听器可以联合式（4）、（5），用各自估计出的时延值τ1和τ2可同时对目标水平距离R和深度H3进行估计。

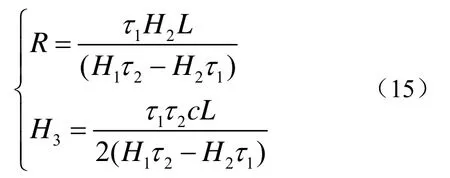
2 仿真分析

2.1 单线谱幅值起伏距离估计

单水听器条件下，假设目标在深度H3=60 m以速度v1=2m/s向x轴负方向运动，接收水听器深度H2=40 m，静止不动，目标与接收水听器初始水平距离为R0=10 km。目标辐射噪声中包含一根线谱，频率为f1=100 Hz，水听器初始接收端线谱信噪比SNR=10 dB，信号强度按照20lg(R0/R)的规律随着运动增加。仿真结果如图2～4所示。

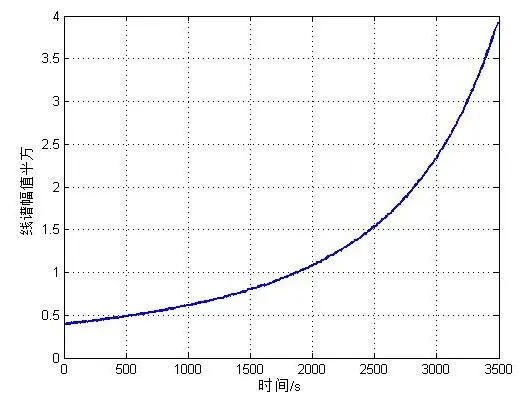
图2 线谱幅值平方测量值

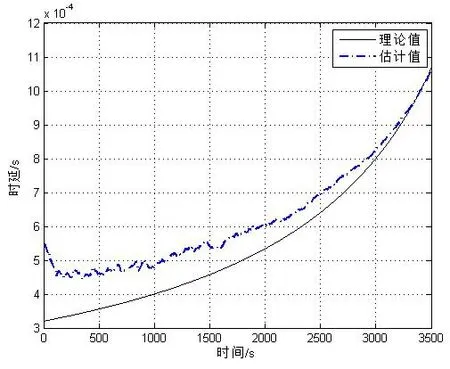
图3 时延估计结果

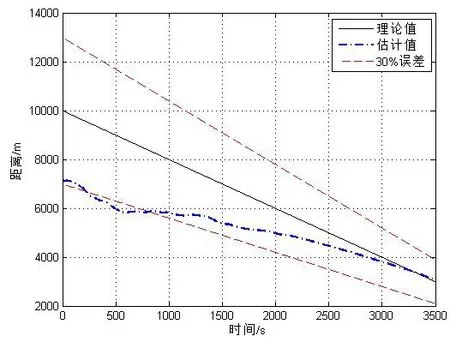
图4 目标水平距离估计结果

2.2 多线谱幅值起伏距离估计

假设目标辐射噪声中含有三根线谱成分，频率分别为f1=100 Hz、f2=150 Hz、f3=200 Hz，初始信噪比分别为10 dB、7 dB、5 dB，衰减规律与运动状态与单线谱时相同。对不同线谱估计出的时延值τ2i，求平均后得出平滑后的时延τ的估计，然后对水平距离进行估计，仿真结果如图5～7所示。

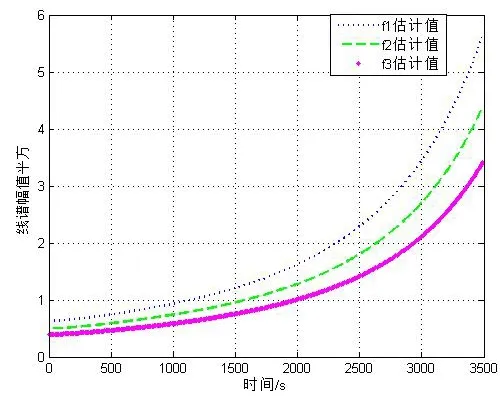
图5 不同线谱幅值平方测量值

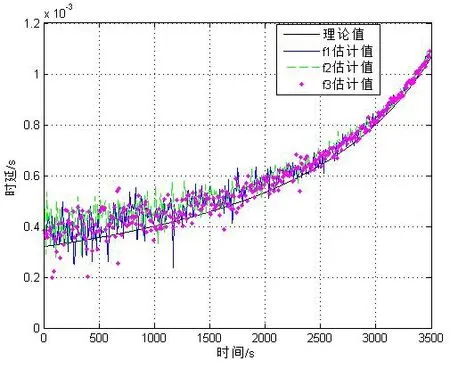
图6 不同线谱时延估计结果

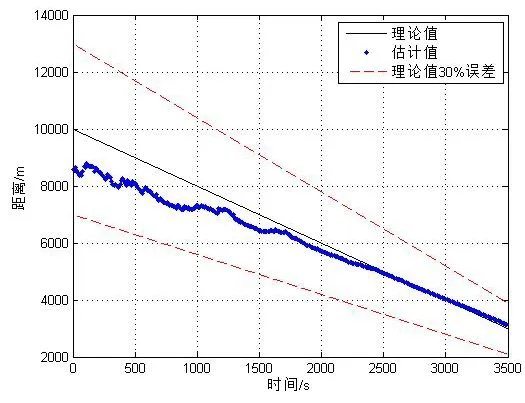
图7 目标水平距离估计结果

从图6可以看出，用不同频率线谱对时延的估计结果相差无几，进一步证明了本文提出的方法对时延的估计性能与频率fi无关，对比图7和图4可以看出，多根线谱估计对时延估计带来的起伏具有平滑效果。

2.3 目标距离与深度估计

双水听器条件下，H1=40 m，L=500 m，其他仿真条件与单水听器时相同，可以实现对目标方位、距离和深度的三维估计。此处省略方位估计，仿真结果如图8～11所示。从图中结果可以看出，使用双水听器或双基阵，可以实现对目标方位、距离和深度的三维估计（此处省略方位估计）。

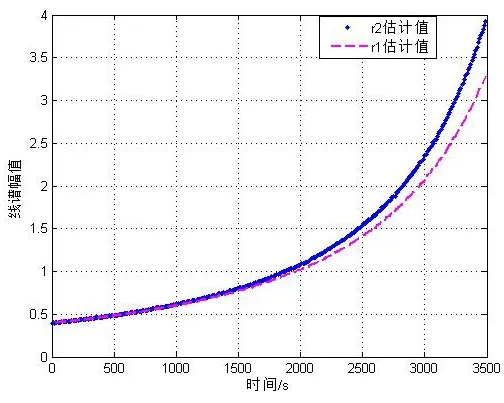
图8 双水听器线谱幅值平方测量值

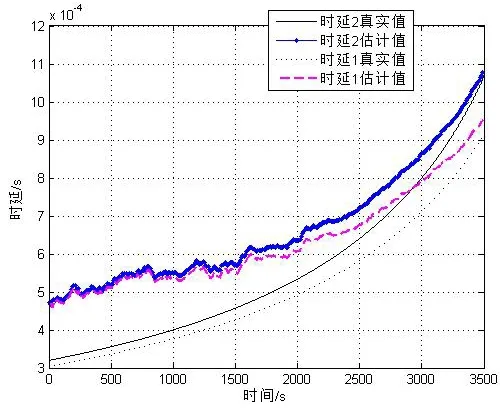
图9 双水听器时延估计结果

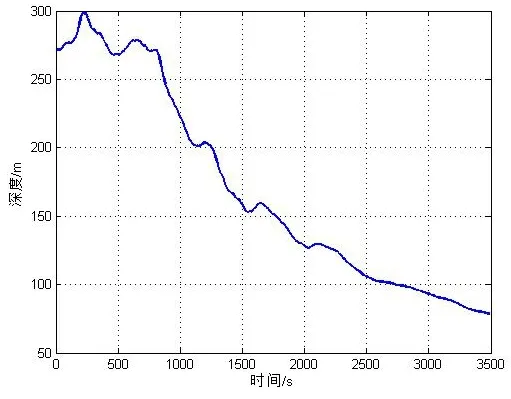
图10 深度估计结果

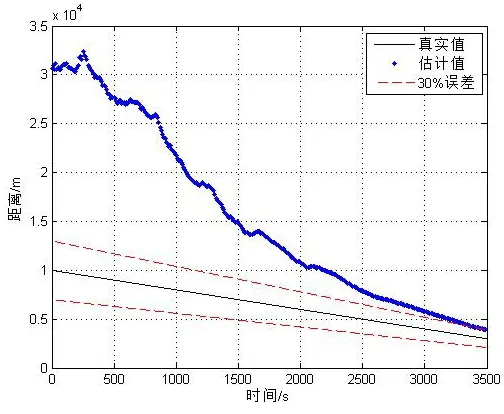
图11 目标距离估计结果

目标距离和深度的估计结果在前期阶段都明显大于真实值，主要是因为当目标距离较远时，两个时延值τ1与τ2的差值很小，如图9所示，使得式（15）的分母非常小，导致对目标距离和深度的估计值偏大，表明在未知深度的情况下，该方法对远距离目标的估计值不准确，但同时，也可以据此推断目标位于较远距离，这对预警、识别和对抗具有重要的意义。

2.4 适用深度仿真

为了分析此方法适用的深度范围，设置H1=H3，选择理论7 000 m处估距误差随着H1+H3的变化情况，结果如图12所示。

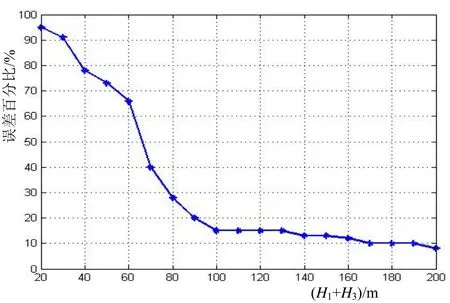
图12 理论7 000 m处误差百分比

图12表明，本方法适用于声源与接收点在一定深度的应用场景，即直达声与海面反射声存在一定的声程差，如潜标对潜预警。

3 结论

本文提出了一种利用线谱幅值起伏估计时延的方法，可以实现对目标距离和深度的估计，该方法计算量很小，在信噪比低、宽带相关失效的情况下有一定的工程应用前景，适用于声源与接收点在一定深度的场景。当对目标的深度信息具有一定的先验知识时，定位结果可以得到显著的改善。