基于空间视线导引法的AUV三维航迹控制技术研究

郭亦平 王益民 林莉 任元洲

（中船重工集团公司第七〇七研究所九江分部，九江市，333005）

水下自主无人航行器已广泛应用于海洋救助、打捞、海洋资源调查、石油开采等民用领域，并可承担扫雷、侦察、情报搜集及海洋探测等军事任务。作为AUV的核心技术之一，运动控制技术得到国内外学者和工程技术人员的广泛关注，并开展了大量的理论研究和工程实践工作。水下航迹跟踪控制是AUV的基本航行模式，主要应用于水下管网巡检、海洋资源调查等场合。高剑[1]基于级联系统理论研究了欠驱动自主无人潜航器的水平面直线航迹跟踪控制和三维直线航迹跟踪控制问题，证明了直线航迹跟踪的全局K指数稳定性。Morten Breivik、Fossen[2]基于视线导引法（Line-of-Sight，LOS）提出了三维路径跟随的制导律实现了三维航迹跟踪控制，Khac Duc Do和Jie Pan[3]利用反步自适应控制方法实现了欠驱动AUV的三维航迹跟踪控制。本文利用空间三维视线导引法，将AUV三维航迹跟踪控制转换为航向跟踪控制和纵倾角跟踪控制，实现了欠驱动AUV的三维航迹跟踪控制。

1 基于空间LOS的三维制导算法

图1所示为AUV的空间三维视线导引法示意图。图中，P为AUV的实际位置，表示期望直线航迹，由图1可知，三维直线航迹跟踪控制的目的为：

图1 AUV的3维直线航迹跟踪LOS

由图1可知，在包含期望航迹线的平面内对AUV实际航行位置进行投影，可消除横向航迹偏差，AUV的指令航向：

式中

为直线航迹线方位角。

按照空间LOS方法，为了消除航迹横向偏差，AUV需以航迹线上某一点作为当前目标点，由此可得

为了消除海流和漂角影响，可在式（3）中引入一积分项，如此可导出如下具有饱和控制作用的航向修正律：垂向航迹偏差控制与航迹横向偏差控制相仿，简述如下：

（2）当前时刻AUV的指令纵倾角可设置为：

式中

（3）为消除海流和攻角影响，可在式（7）中引入一积分项，可得修正后的指令纵倾角为：

当AUV沿着直线航迹航行到距下一航路点一定距离的时候，需要进行航路点切换，切换机制有两种实现方式：

（1）当AUV的位置与直线航路点Pi的距离与两个航路点距离的差小于某一设定值时，则当选择下一航路点，即

一般而言，可选Ri+1=(1.5~5)L，L为AUV的艇长。

（2）可参照文献[4]的椭球切换机制选择下一航路点，即

2 纵倾MPC控制算法

本文中AUV的纵倾控制和航向控制均采用一种基于拉盖尔（Laguerre）函数逼近的MPC方法[5]，该方法可大幅减少计算负担，因而可用于AUV自主航行控制系统中。航向MPC控制算法的设计可参照文献[6]。

一般具有鱼雷外形的欠驱动AUV仅配置十字型尾鳍对航向、纵倾实施控制。理论研究表明， 这种AUV的垂直面运动与水平面运动耦合性较小，因而AUV垂直面运动线性方程可用状态空间方程描述如下：

式中，w为垂向速度；q为纵倾变化率；θ为纵倾角；δs为艉水平鳍角。式（13）和式（14）简记为

式中：

利用后向差分法离散化式（15）后，可得

将式（16）离散化两端差分运算后，可得

引入如下符号：

则可由式（18）得如下增量式状态方程和状态输出方程：

上式简记为

假设在k时刻的m个采样间隔后解算的预测指令鳍角增量为

拉盖尔函数向量具有下述正交特性

假设在k时刻，式（20）的状态为则在此时刻的m个采样间隔的预测状态为

为设计纵倾预测控制律，设代价函数为

将式（23）所述预测状态代入上述代价函数，可得

则利用拉盖尔函数的正交特性，可得

考虑到控制纵倾的尾鳍在施加运动控制过程中存在角度和角速度物理限制，因而，上述代价函数的求解需考虑下述物理约束：

鳍角约束不等式为：

上式可简记为：

鳍速约束不等式为：

上式可简记为：

将式（28）和上式联立后简记为：

则纵倾MPC控制器的求解问题转换为二次规划问题：

该二次规划问题可采用活动集法求解，可利用Hildreth二次规划方法[7]。故纵倾MPC控制器可设计为：

由于一般廉价的AUV出于性价比考虑，不安装速率陀螺和加速度计等测量装置，不具备垂向速度w和纵倾角速度q的测量能力，故需设计状态观测器进行状态估计，状态观测器的设计可利用离散时间卡尔曼估计理论设计[8]：

3 仿真分析

为了验证本文提出的三维航迹控制算法的有效性，利用文献[8]中的AUV运动数学模型进行仿真验证。设计了多折线式三维空间搜索任务，选择如下航路点：

上述12个三维航路点中，A点为预定航行任务的起点，B~L为待完成的航路点。控制任务为使AUV沿12个航路点依次连接的航迹进行运动。试验初始条件为：初始位置（-820,90,35）m，初始方位角20°，航速3 kn。三维航迹控制效果见图2~5。

图2 三维航迹变化图

图3 水平面投影

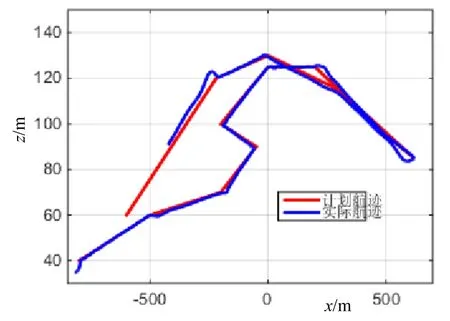
图4 垂直面投影

图5 轨迹侧向与法向偏差

由图2可以看出，AUV在整个航行过程中都能够跟踪航路点，无论航迹侧向偏差还是垂向偏差都能够逐渐收敛，航迹贴合度良好。由图5轨迹侧向与法向偏差变化图中可以看出，在搜索过程中，最大航迹侧向偏差为22 m，发生在航路段DE向航路段EF切换过程中。一般而言，在航路段切换过程中，不对航迹侧向跟踪偏差进行考核，若仅考核直线航路段的航迹稳定精度，则以AB航路段为考核段，其航迹稳定精度仅为0.066 m（RMS值）。由图5还可以看出，在搜索过程中，最大法向偏差为7 m，也以直线航路段AB航路段作为考核段，则法向航路段法向跟踪稳定精度为0.1 074 m（RMS值），对于仅装备深度传感器和纵横倾仪的AUV而言，侧向轨迹偏差和法向轨迹偏差这两项性能指标均可满足工程使用要求。

由图6~9可知，在三维航迹跟踪控制过程中，航向角的跟踪控制非常平稳。图6、7中，航向大幅变化，艉垂直鳍能够平稳控制AUV改变并保持航向。航向修正过程中，超调量仅为2.23%，完全满足一般AUV航向超调量10%的性能指标要求。从图8、9可知，航迹跟踪控制过程的16次较大指令纵倾变化，实际纵倾角都能够快速跟踪指令纵倾角，且水平鳍出鳍收鳍动作平稳，表明本文所设计的纵倾MPC控制算法具有较好的控制性能和控制品质。结合图2~5可知，本文提出的空间LOS制导算法能够适用于AUV的三维航迹跟踪控制，具有良好的控制性能。

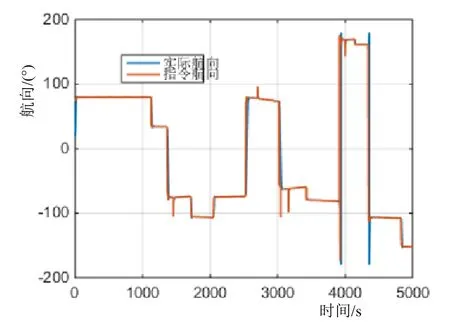
图6 航向变化曲线

图7 艉垂直鳍角变化曲线

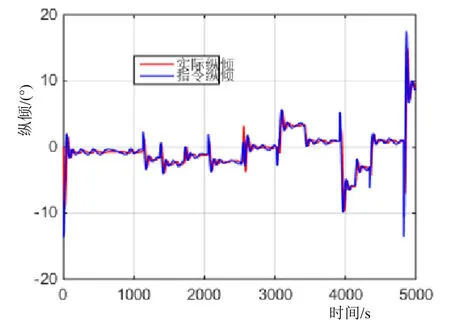
图8 纵倾变化曲线

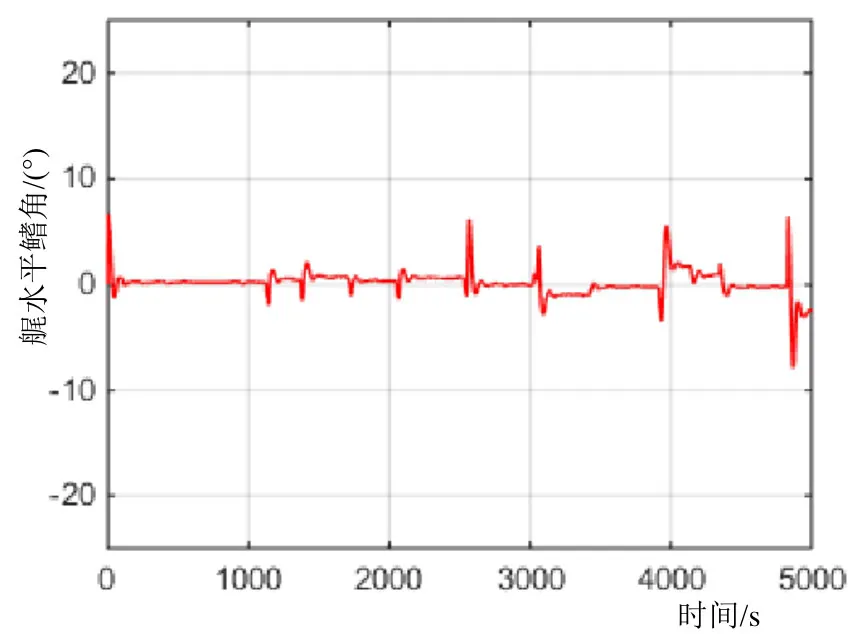
图9 艉水平鳍角变化曲线

4 结论

本文针对AUV三维航迹跟踪控制问题，利用空间视线导引法，将航迹横向和垂向偏差的跟踪控制转换为航向跟踪控制和纵倾跟踪控制，提出了基于LOS的空间航迹跟踪制导算法；基于垂直面线性运动数学模型，设计了纵倾MPC控制算法，实现了AUV的空间轨迹跟踪控制。仿真结果表明：（1）文中设计的空间LOS制导算法计算简洁，有较高的工程实用价值；（2）文中提出的三维航迹跟踪控制具有较好的航迹控制性能，能够满足工程使用要求；（3）文中设计的纵倾MPC控制算法，利用拉盖尔网络逼近方法和Hildreth二次规划方法，具有良好的控制性能和控制品质，有较大的工程实用价值。