基于边缘频率分布互相关系数的水声跳频信号检测方法

张刚强 张俊清 刘俊凯 张伟

(水声对抗技术重点实验室 上海船舶电子设备研究所，上海，201108）

水声通信信号的检测是对其进行参数估计、干扰的前提。针对水声通信中常用的跳频通信信号，目前常用的检测方法主要可分为两大类：能量检测方法[1]和自相关检测方法[2，3]。后者较前者在检测性能上有一定的提升，而且还降低了运算复杂度。其中单跳自相关需要已知跳频信号的跳频率，但是在信号非合作检测中，跳频信号的参数是未知的，多跳自相关技术无需预知跳频信号的功率、跳频图案、跳频率等参数，而只需预知信号带宽，因此具有更广的应用范围。基于多跳自相关技术，研究者提出“多跳功率和”等不同检测量[4]，但检测量的求取过程较为复杂，且判决门限的确定和信噪比密切相关，实际实施存在不便。本文提出一种以边缘频率分布互相关系数作为检测统计量的水声跳频信号检测方法来解决上述技术问题。

1 原理

基于互相关系数的多跳自相关检测流程图如图1所示。

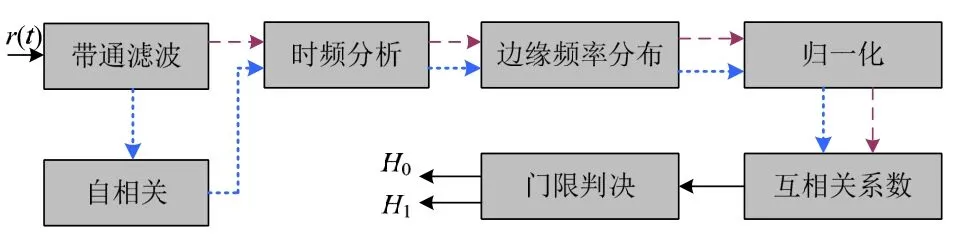
图1 基于多跳自相关的跳频检测流程图

带通滤波后的跳频信号rBP(t)为

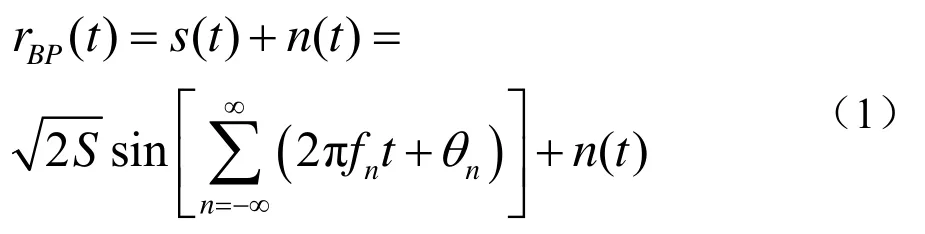
式中，τ为延迟时间、*代表共轭运算，T为rBP(t)时间长度。跳频接收信号时频分析结果的边缘频率分布：

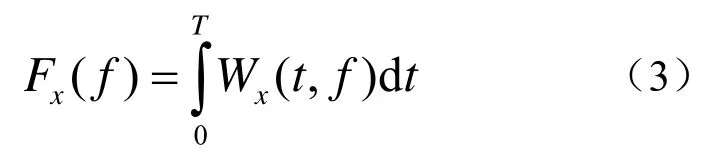
对跳频接收信号求自相关信号，信号的观测时间为T，则多跳自相关输出为

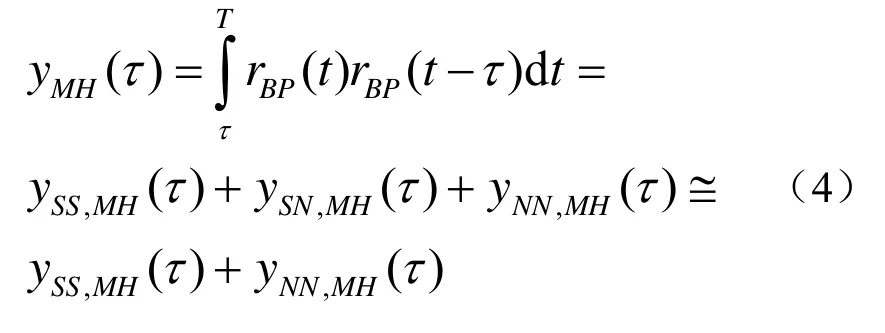
式中，ySS，MH(τ)是自相关信号中的信号乘信号分量、ySN，MH(τ)是信号乘噪声分量、yNN，MH(τ)是噪声乘噪声分量。在跳频增益和跳频带宽都很大的情况下，在观测期T内，跳频信号的频率在相邻几个跳周期之间是互不相同的，故τ＞TH时，ySS，MH(τ)≅0；τ＜TH时，跳频信号在一个跳频间隔内是相关的，ySS，MH(τ)值非零，可表示为

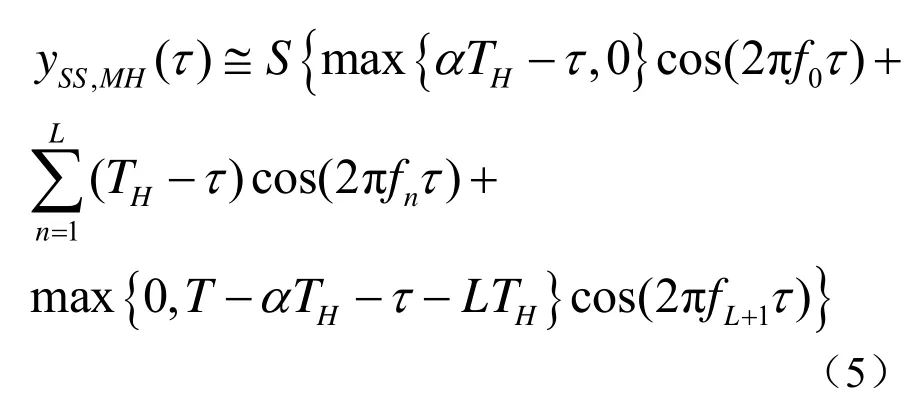
式中，L是观测期T所包含的完整的跳频个数。计算的时频分布：

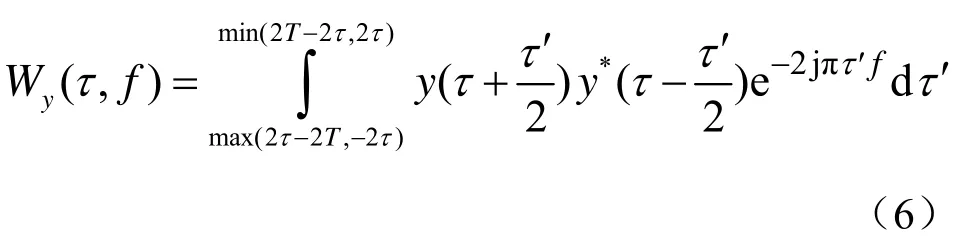
式中，τ′代表延迟时间。跳频多跳自相关信号时频分析结果的边缘频率分布为

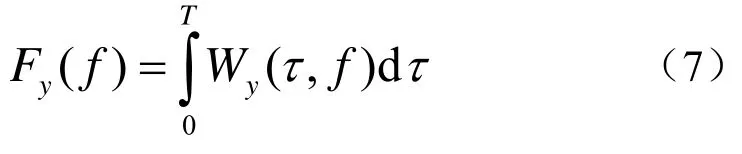
对式（6）、（7）所得边缘频率分布进行归一化处理：

所得归一化边缘频率分布的互相关系数为

2 仿真分析

通过计算机仿真分析验证本文检测方法的有效性。仿真参数设定如下：码元间隔2.5 ms，跳频周期27.5 ms，共有11个跳频频点，检测时，观察时间与跳频周期一致。发射信号的时频图如图2所示。

检测中确定检验统计量（本文检验统计量为互相关系数）门限的方法为：在特定噪声功率水平和给定的虚警概率PF指标要求条件下，进行Monte Carlo仿真，仿真次数为N，即产生N段特定时间长度和功率的噪声，分别计算N段信号的检验统计量，再对统计量进行降序排列，得到序列ρn，n=1，2，...，N，则使得虚警概率PF的检验统计量门限G取值范围为

图2 发射信号时频分析

以本文仿真为例，假定信号功率为1，噪声功率为-16～20 dB（间隔2 dB），若要求虚警概率为0.001，则依据上述方法求得各个噪声功率水平下的互相关系数门限为

标准差为0.004 3，表明边缘频率分布互相关系数门限随信噪比的变化不大。如图3所示，当信噪比大于0时，多次仿真结果表明，互相关系数总是大于0.95。图4中，门限为0.95，当信噪比大于-2 dB时，检测概率为100%。

图3 边缘频率分布互相关系数

图4 跳频信号随信噪比检测概率

3 总结

对跳频信号时频分析结果进行边缘频率分布计算，得到了一定观察时间内曾出现的各频率信号功率随时间累积的结果，可称为该信号的频点能量图；对跳频信号自相关运算的时频分析结果进行边缘频率分布计算，得到了自相关信号功率随延迟时间累积的结果，可称为该信号的自相关频点能量图。由于单频信号自相关运算不改变信号频率，当延迟时间小于1个跳周期时，跳频信号和其延迟信号的自相关结果近似为信号观察时间内曾出现的各频率信号的叠加，因此自相关频点能量图结构上近似与频点能量图相同。通过频点能量图和自相关频点能量图互相关系数与门限进行比较，可以确定跳频信号的有无。由于自相关运算具有一定的抑制噪声的能力，降低了噪声对频点能量图和自相关频点能量图互相关系数的影响，仿真结果验证了该观点。仿真结果同时表明，当信噪比大于0时，互相关系数总是大于0.95。当取门限为0.95，信噪比大于-2 dB时，检测概率为100%。本文提出的基于边缘频率分布互相关系数的检测统计量门限随信噪比变化不大，因此在水声跳频信号非合作检测场合具有一定的实用意义。