基于卷积神经网络的移动对象目的地预测

江 婧,张怀峰,皮德常

(南京航空航天大学 计算机科学与技术学院,南京 211106)

1 引 言

随着移动传感器(如手机,GPS)的普及,人们越来越多地受益于各种基于位置的服务.移动设备所配备的位置传感器利用全球定位系统精准的提供了用户的位置,不同时间戳的位置形成用户的日常活动轨迹.这种轨迹数据具有高度时间和空间规律,为许多基于位置的应用的出现和改进提供了数据来源.大量新型的基于位置的应用都需要对目的地和未来路线进行预测,例如,推荐旅游景点,获取用户可能感兴趣的附近场所,基于目的地发送针对性的广告等.此外,文献[1]和文献[2]还将目的地预测应用于判断是否偏离了预定路线、捕捉汽车盗贼.

目的地的预测通常需要使用到历史轨迹,如果所要查询的轨迹与历史轨迹中出现的某一部分相匹配,那么这部分轨迹的目的地很可能也是所查询轨迹的目的地.贝叶斯模型[3-5]和马尔科夫模型[6,7]一直以来被广泛应用于目的地预测,此外,文献[8]从轨迹中学习相关的移动模式构建出T-pattern决策树,通过从树中查找最佳匹配路径来预测新轨迹的下一个位置.文献[9]提出了一种最近邻轨迹(NNT)技术,识别与当前车辆部分轨迹最相似的历史轨迹,然后根据历史轨迹来预测车辆未来的移动.文献[10]首先对历史轨迹进行聚类,随后将拟查询轨迹分配到最可能属于的簇,通过学习簇内轨迹的特征来对目的地进行预测.

尽管上述方法通过对历史轨迹模式的学习,有效地实现

1https://www.kaggle.com/c/pkdd-15-predict-taxi-service-trajectory-i

目的地预测,但都忽略了预测过程中“数据稀疏问题”所带来的影响.也就是说,由于现有数据集中历史轨迹数量有限,所要查询的路线很难与历史轨迹完全匹配,相同的目的地可能通过不同的路径所到达;即使查询轨迹与历史轨迹的一部分完全匹配,目的地也很可能不同.

为了解决数据稀疏问题,一些学者借助外部信息来改善预测效果,如结合道路网络信息和车辆行驶信息,根据道路结构和走向以及行驶速度进行分析,或根据用户历史信息确定其个人喜好从而对目的地进行推荐[3,11,12].由于有时并不能准确地获取这些信息,Xue等人在未使用外部信息的情况下,提出了SubSyn[13]及其改进算法[5,14],将历史轨迹分解成由两个相邻位置构成的子轨迹,子轨迹被重构形成合成轨迹,然后建立马尔可夫模型量化相邻位置之间的相关性,该过程可有效扩展历史轨迹数据集的数量.Wang等人[11]基于最优化理论中的梯度下降原理,提出MGDPre算法,通过分析查询轨迹采样点位置与最终目的地之间的距离变化,实现对稀疏轨迹集的目的地预测.Li等人[15]构建镜像吸收马尔科夫链模型对轨迹进行建模,并引入上下文感知张量分解方法,有效解决了目的地预测时的轨迹稀疏问题.

此外,大部分文献都将轨迹数据作为一维的时空点序列进行分析.这样的一维结构虽然简洁,但在一定程度上限制了从中了解其他详细的信息.在一维轨迹序列中,只能获取各个时间点移动对象的位置信息,以及轨迹点的先后关系,并不能了解轨迹在平面图上的整体形态,也无法看出移动对象何时拐弯、何时绕行等.正如常言道,“一图胜千言”.本文将一维轨迹序列转换为二维像素图像,利用这种可视化的方式向人们更清晰地展示了轨迹的整体走向和终点位置,通过挖掘轨迹图像的空间特征来确定目的地的位置.

本文使用Kaggle-ECML/PKDD竞赛数据集1,并与该竞赛冠军团队的预测结果[16]进行对比.竞赛获胜团队通过构建多层感知机(MLP)实现对目的地坐标的预测,他们选取轨迹前5个点和后5个点的经度和纬度,结合驾驶员ID、客户信息等其它相关信息,以一维向量的形式输入MLP,最终以Custom Test=2.81,Kaggle Public=2.39,Kaggle Private=1.87的测试误差获得第一名.但是,竞赛方法的输入向量所含信息量有限,仅将起点和终点附近5个GPS点经纬度转换为两个一维向量,虽然结合了其他信息,仍旧不能很好的表示轨迹的特征,这对最终的预测精度造成了一定的影响.

本文针对以上缺点和限制,基于卷积神经网络(CNN)实现了移动对象目的地的准确预测.文章的主要贡献如下:

·本文将一维轨迹序列转换为二维像素图像,通过构建CNN来实现特征的提取和目的地预测.不同于传统文献中直接对一维轨迹序列进行分析,本文从二维像素图片中可以获取更多空间模式和移动对象运动的细节信息,CNN从图像中提取出的高阶特征更有助于之后的预测任务.

·“数据稀疏”作为目的地预测中最常见的问题,在很多文献中都没有得到很好的解决.本文在对轨迹数据进行处理的过程中,先后引入PMDL和PRT算法,有效地克服了目的地预测时的数据稀疏问题.

·本文未将完整的轨迹图像直接输入模型进行学习,而是先对局部特征的重要程度进行分析,然后截取重要特征附近区域作为模型的输入.本文对重要特征区域的大小进行了探讨,并找到最佳局部特征范围,在一定程度上提高了预测的准确率.

文章后续内容由以下几部分组成,第二部分给出了相关术语定义和问题陈述,第三部分详细介绍本文的模型方法,第四部分呈现了实验设置和实验结果,第五部分对文章进行了总结和展望.

2 问题定义

本节定义了相关术语和需要解决的问题.

问题1.数据稀疏问题

数据稀疏问题是在实现目的地预测时很常见的问题之一.在将查询轨迹与历史轨迹进行匹配时,现有的历史轨迹远远不足以覆盖所有可能的查询轨迹,从而影响对轨迹目的地位置预测的精度.数据稀疏性可能由以下几种原因造成:

第一,数据集中给出的历史轨迹数量有限,只能覆盖一部分所要查询的轨迹.例如,已知历史轨迹tra1:A→B→C,tra2:A→D→E→F,tra3:A→D→E→G.当查询tra4:A→B时,它与tra1的一部分完全重合,可以认为它的目的地很可能与tra1相同,即目的地为C;当查询tra5:A→D→E时,它和tra2,tra3的其中一部分都相同,因此它的目的地可能是F也可能是G.

第二,在划分网格上表示轨迹数据时,由于二维空间数据的多尺度特性,在不同尺寸的网格图中,轨迹会呈现出不同的模式.如图1所示,可以明显地看出不同尺寸的网格中各轨迹的形态有明显差异.在图1(a)较小的尺寸下,各轨迹的细节信息变得更加显著,导致轨迹重叠程度较低,几乎不能保证查询轨迹与历史轨迹中的某部分完全重合.在图1(b)较大的尺寸下,所有轨迹的细节被缩小,轨迹重叠程度增加,对目的地预测造成了很大的难度.因此,网格尺寸也会导致数据稀疏问题.

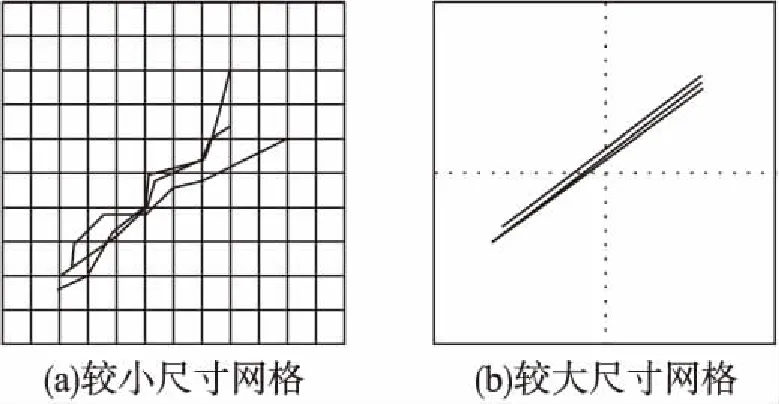
图1 不同尺寸网格下的轨迹形态Fig.1 Trajectory patterns in different size of grid

第三,当每条轨迹的采样频率不同时,有些轨迹的特征表示非常详细,但有些轨迹却表示的过于简略.即使两段轨迹的起点和终点相同,由于特征表示的详细程度不同,网格图像上表示出来的路线也很可能有很大的差异.

为了解决以上情况导致的“数据稀疏问题”,本文首先对轨迹进行分段表示,在保留原始信息的同时,最大程度降低相似轨迹之间的差异;然后用尽可能小的网格将轨迹表示成像素图片,以免丢失大量细节信息.具体算法见3.1和3.2节.

问题2.轨迹目的地预测问题

预测任务要求根据测试集给出的不完整的轨迹段,来预测可能的目的地坐标.这很容易联想到直接对经度和纬度这一对数值进行预测.当使用神经网络解决这类问题时,这意味着输出层由两个神经元组成.然而,由于模型的输入所含信息量有限,仅根据现有的信息,很难对目的地坐标直接进行计算.

为了解决这个问题,本文为所有轨迹图像增加标签,将对原始不带标签的轨迹目的地预测问题,转化成一个有监督的轨迹分类问题,这在一定程度降低了直接对坐标进行预测的难度.具体见3.2节.

3 基于CNN 的目的地预测

目的地的预测通常需要使用历史轨迹,当所要查询的轨迹与历史轨迹中的某一部分相匹配时,可以认为这部分轨迹的目的地很可能也是所查询轨迹的目的地.由第2节对问题1的描述可知,数据集中轨迹数量有限,网格的尺寸和轨迹的采样频率影响了轨迹表示之间的差异,这些都限制了对轨迹的有效匹配.但是,数据集的样本量以及轨迹的采样频率都不由实验者决定,找到最优网格尺寸也并不是一件容易的事情.即使找到了最优网格尺寸,由于每条轨迹本身的总采样点数目就不是很多,用像素图像表示轨迹时也很可能丢失大量信息.

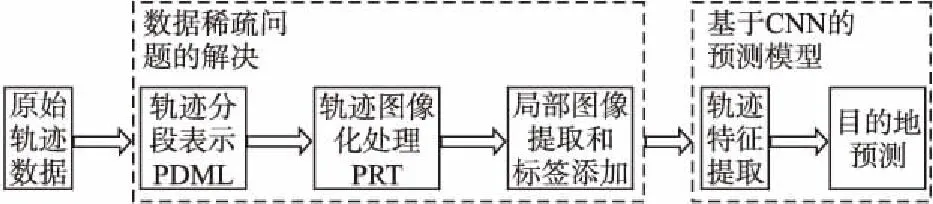
图2 基于CNN的目的地预测流程Fig.2 Overview of destination prediction based on CNN

本文按照图2的流程,在解决了上述“数据稀疏问题”,防止大量信息丢失的同时,对轨迹目的地进行了准确预测.首先,引入参数化最小描述长度策略(PMDL)对原始轨迹进行最优分段表示,在最大程度保留原始轨迹特征的情况下,减少相似轨迹之间的差异性并增加不同轨迹之间的差异程度,具体见3.1节;随后,提出轨迹的像素化表示方法(PRT),将原始轨迹数据处理成像素图片,截取其起点和终点附近的区域作为输入,并增加类别标记,具体见3.2节;最后,使用CNN对轨迹图片进行特征提取和目的地预测,具体见3.3节.

3.1 轨迹的分段表示

轨迹分段即从一条轨迹ti=p1p2…pj…pleni中找出特征点集,也就是轨迹某一处变化很大的点的集合,通过连接相邻的两个特征点形成轨迹的分段表示.最优的轨迹分段要求同时具有精确性和简洁性.

文献[17]提出使用最小描述长度(Minimum description length,MDL)原理来找到最佳分段方案.MDL原理包含两个部分:L(H)和L(D|H).其中H是假设,D是数据.L(H)用来描述假设的长度,L(D|H)是在假设为H的情况下对数据D进行编码后,数据D编码的长度.当L(H)与L(D|H)的和最小时,此时H是能够解释数据D的最佳的假设.

在本文的轨迹分段中,原始轨迹相当于MDL原理中的数据D,对原始轨迹的分段相当于MDL原理中的假设H,找到最佳轨迹分段即为找到一个使L(H)+L(D|H)最小的轨迹分段.考虑到实际应用对精确性和简洁性有不同的要求,当轨迹数据量较小时,通常要求简洁性低而精确性高;当数据量较大,通常要求简洁性高而精确性低.此外,按照MDL原理只能找到一个使L(H)+L(D|H)较小的近似轨迹分段,因此本文对MDL进行改进,提出了参数化最小描述长度策略(Parameterized Minimum Description Length,PMDL).

PMDL以uL(H)+vL(D|H)代替L(H)+L(D|H),即找到一个分段,使得uL(H)+vL(D|H)(u,v≥0,且u,v为实数)最小,则该分段就是最佳分段.L(H)和L(D|H)分别由公式(1)、公式(2)给出.当u/v>1 时,得到的最佳分段简洁性较高,考虑极端情况,当u/v→∞,即v=0时,此时得到的轨迹分段即为原始轨迹起点和终点的连线,这种情况下简洁性最高而精确性最低;当u/v<1时,得到的最佳分段精确性较高,考虑极端情况,当u/v=0即u=0时,此时得到的轨迹分段即为原始轨迹,这种情况下精确性最高而简洁性最低.根据上述分析,可以根据具体需要来调整u,v的大小,使轨迹分段的简洁性和精确性满足需求.

(1)

(2)

将图Gi视为轨迹ti中所有点组成的一个无向完全图,其中边pipj的权重w(pipj)由uL(H)+vL(D|H)计算得出,则求最佳分段相当于求图Gi中以p1为起点,pleni为终点的最短路径,即该最短路径就是对该轨迹的最佳分段.因此,可以使用著名的Dijkstra算法求得最佳分段.图3展示了将最佳分段问题建模为最短路径问题的一个示例.

图3(a)为一条包含了4个点的轨迹,任意给定该轨迹的两个点,都可以求出这两点的L(H)和L(D|H).因此,对于图3(b)中的无向完全图,每条边上的权重L(H)+L(D|H)都可以计算出.从而,根据PMDL求出的最佳分段,也就是图3(b)中无向完全图从点p1到点p4的最短路径.

根据上述思路,本节对原始轨迹进行了最佳分段表示,削弱了相似轨迹之间的差异性,同时也保留了原始轨迹的重要特征.

3.2 从一维轨迹到二维图像

根据上一节提出的PMDL算法,得到了原始轨迹的最优分段表示.在没有相应道路网络信息的情况下,为避免上文所述的数据稀疏问题,本小节进一步对分段表示的轨迹进行处理,用尽可能小尺寸划分的网格将其表示成黑白像素图片,作为最终的模型输入.这样不仅在一定程度上克服了轨迹数据稀疏,还减少了图像转换过程中的信息丢失.

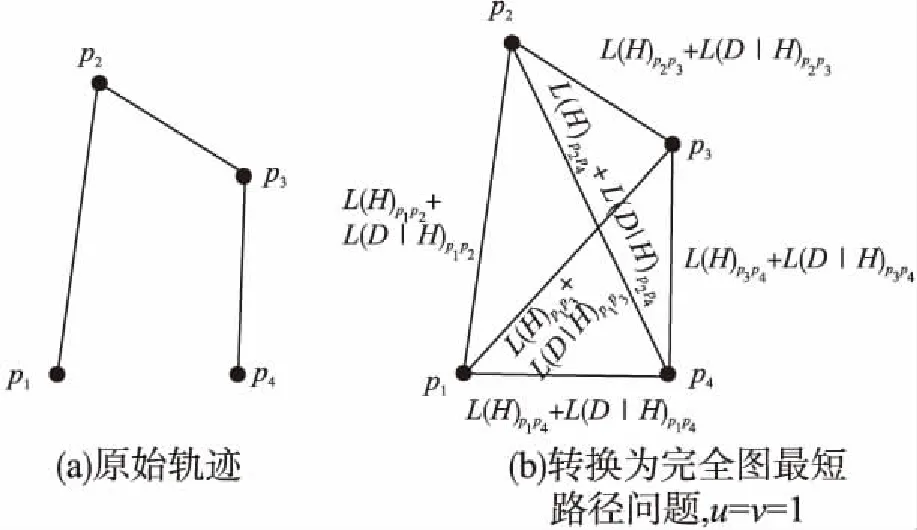
图3 PMDL将最佳分段问题建模为最短路径问题的示例Fig.3 An example of trajectory segmentation problem and the corresponding shortest path problem

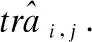
算法.Pixel Representation of Trajectory(PRT)

输入:轨迹数据trai,j

网格边长L

输出:轨迹的像素矩阵G

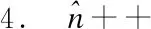
5.forallk=1 ton-1do

//vis the direction vector of X axis

7.s=L

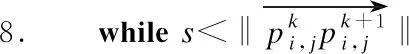
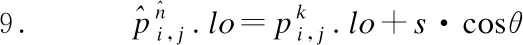
11.s=s+L

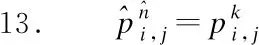
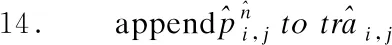
16.end

17.endfor

18.G=zeros(M,M)

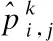
21.G(cx,cy)=1

22.endfor

23.returnG

3.3 局部图像提取和标签添加

为了实现目的地预测,通常需要通过学习历史轨迹的特征,来对未知轨迹进行匹配,从而确定查询轨迹的最终目的地坐标.当查询轨迹与历史轨迹进行匹配时,可能存在以下几种情况:

1)整条查询轨迹段与历史轨迹的某一部分完全相似,目的地很可能相同;

2)查询轨迹段与历史轨迹的出发点附近或者中间部分相似,但最终的目的地不同;

3)查询轨迹与历史轨迹前端部分不同,但终点附近轨迹相似,目的地可能相同.

考虑以上三种情况,直接将数据集中整段轨迹的图像输入到分类器中进行学习是不合理的,终点相同的两条轨迹,其整体相似度不一定很高;反之,相似度较高的两条轨迹目的地未必相同.

这很容易联想到,从轨迹中提取出对最终预测结果影响较大的部分,而不是将整段轨迹作为特征输入到模型中进行学习.文献[18,19]通过可视化卷积网络,获取了不同层卷积所捕获的轨迹图像特征的具体含义,并得出靠近轨迹起始点和终点的局部区域对预测结果有更大决定作用的结论.起始点在某种程度上显示出旅途的动机;靠近终点的轨迹显示目的地的趋向.因此,本文选择将轨迹起点和终点附近的局部区域图像作为最终的输入图片.

正如第2节问题2所描述,预测任务要求在已知部分轨迹段的情况下,预测出该轨迹的最终目的地坐标.最直接的想法是对经纬度这一对数值进行预测,这在神经网络中意味着输出层由两个神经元组成.由于模型输入的信息量有限,这种方法给预测工作带来了非常大的难度.受到竞赛冠军方法的启发,本文采用了一种不同于传统的目的地预测问题的方法,首先对训练集轨迹终点进行mean-shift聚类,将每个簇的聚类中心作为该簇中所有轨迹的目的地坐标,相当于为每条轨迹加上标签;然后对查询轨迹进行有监督训练.这样就避免了直接对目的地坐标的预测,将无标签的轨迹终点预测问题转换为有标签的分类问题,在一定程度上降低了预测难度,提升了算法的可行性.

值得注意的一点是,在竞赛冠军方法中,数据集中所有轨迹的终点被划分成3392个簇.但是,划分的簇的数量多并不意味着预测效果就好,文献[10]通过实验验证了这一点,并找到了最佳划分的簇数应为45.因此,本文将45作为轨迹目的地聚类的簇数.

3.4 基于CNN的预测模型

近年来深度学习在图像识别、语音识别、目标检测、自然语言处理等领域取得了巨大的成功,但是很少有学者将其应用到轨迹数据的处理尤其是目的地预测的问题上.卷积神经网络(Convolutional Neural Networks,CNN)作为一种深度学习模型,它集特征提取与分类于一体,使用多个卷积层和池化层从训练数据中自动提取复杂的高维特征,然后对其进行分类.

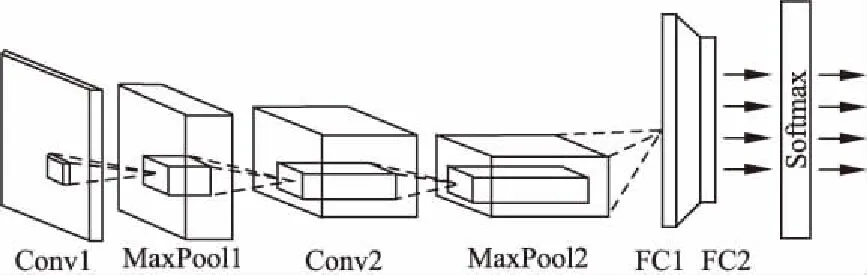
图4 基于目的地预测的CNN模型结构图Fig.4 Structure diagram of destination prediction based on CNN

本文设计了一个简单的CNN结构,如图4所示,由两层卷积层,两层池化层,两层全连接层和一层输出层组成,其中每个池化层直接连接在卷积层之后.详细参数如表1所示.输入是大小为60×60的双通道轨迹图片,分别代表起点和终点附近所截取的区域.输入图片经过卷积层Conv1大小为5×5,步长为1的卷积核处理,得到16个大小为56×56的特征映射.池化层MaxPool1通过大小为2×2,步长为2的过滤器,使用最大池化提取出最显著的特征.后两层Conv1,MaxPool1的操作与前两层相同.最终提取的特征依次与包含100个神经元和50个神经元的两层全连接层FC1,FC2相连接,最后通过一个Softmax函数区分出各个类别.

表1 CNN相关参数取值
Table 1 Values of related parameters in CNN

Layer NameNo.of neuronsKernel size for each feature mapStrideInput Lay-er60×60×2--Conv156×56×1651MaxPool128×28×1622Conv224×24×3251MaxPool212×12×3222FC1100--FC250--

4 实验及分析

4.1 数据集设置

本文的实验数据来源于Kaggle-ECML/PKDD竞赛中的真实轨迹数据集.该数据集提供了442辆出租车在葡萄牙波尔图市一整年(01/07/2013-30/06/2014)的行车轨迹.这些出租车均安装了移动数据终端,精确的定位了他们在不同时间戳的坐标.训练集包含了170万个样本点,每一个样本都对应一个完整的行程,共包含了了客户信息、客户请求服务的方式、乘车站台、节假日等9个属性.为了使本文提出的方法对大多数轨迹数据集都具有适应性,本文仅使用各个时间戳对应坐标值所组成的轨迹来实现目的地预测.

为了使预测结果更具说服力,本文采用和文献[16]相同的划分方式,从训练集中随机选取19427条轨迹作为验证集,19770条轨迹作为测试集,其余的作为训练集.本文同样使用Haversine距离来评价预测目的地与真实目的地之间的距离.Haversine距离根据纬度和经度测量球面上两点的距离,其公式定义如下,λx,Φx分别为点x的经、纬度,R是地球半径:

(3)

其中：

(4)

4.2 输入图片的大小确定

为了确定合适的输入图片大小,本文从起点和终点附近截取不同尺寸的区域作为输入,分别输入模型进行预测.截取区域的方法如下:分别以轨迹起点和终点为圆心,轨迹长度的N%为半径R画圆,并以包含该圆的最小矩形区域为输入图片.也就是说,当该圆的外切矩形恰巧包含了完整的方格时,取该外切矩形区域作为输入;如果外切矩形包含不完整的小方格,那么就以最小的长度增加矩形边长,使之恰巧包含完整的方格.随后,将所有轨迹被截取的区域处理成相同大小的图片,就得到了最终输入的轨迹图像.图5为从一条轨迹中所截取的不同大小区域图片的示意图,截取后的两部分作为一个双通道的图像输入CNN模型中.

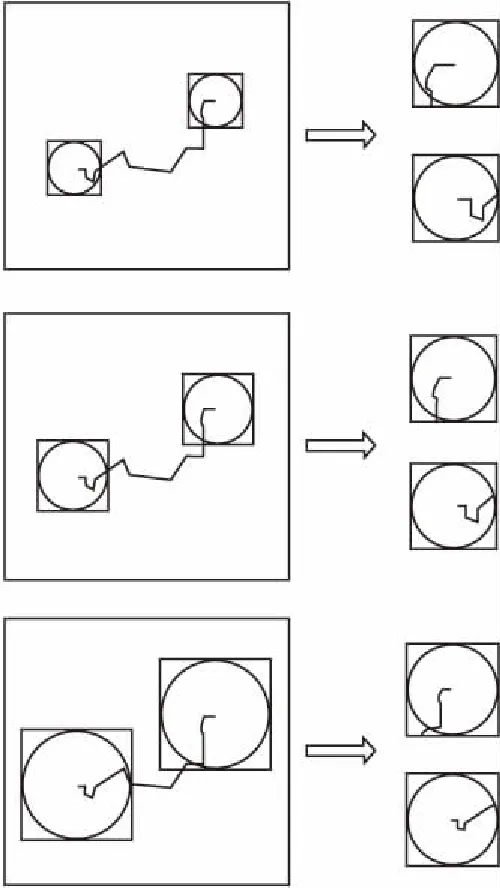
图5 轨迹中截取的三种不同大小区域图片的示意图Fig.5 Three different size of regions in trajectory

通过截取起点和终点附近不同大小的区域,并将它们输入到CNN中对目的地进行预测,得到不同大小区域作为输入对应的预测误差,如表2所示.从表2中可以看出,截取长度过长或过短都是不合适的,当截取的部分太短(R=10%,20%)时,获取的信息不足以对轨迹进行有效预测,当截取的部分太长(R=50%)时,相当于把原始轨迹分割成两段作为输入.通过对预测误差的对比可知,当以轨迹长度25%的比例截取起点和终点附近的区域作为输入时,表现效果相对最好,本文将其作为本文的最终截取比例,并将最终输入图片大小设置为60×60.

表2 不同大小输入图片对应的预测误差
Table 2 Prediction errors in different size of input

R=N%10202530354050误差(105km)3.552.891.982.072.533.293.87

4.3 模型的训练与测试

模型每个训练批次的样本个数为60,训练轮数为400,正则化参数,学习率和动量参数分别设置为0.2,0.001和0.7.训练过程中误差随着训练轮数增加而逐渐减小,500轮训练之后,训练误差和验证误差都达到稳定,此时模型训练完毕.

为了验证所提出方法的有效性,同时便于与其他文献结果进行比较,本文采用两种方法对模型进行测试.

第一种方法是从测试集中提取出的不同比例长度的轨迹前缀,对它们分别进行预测,预测误差变化如图6所示.图中Proposed1是将整段已知轨迹的像素图片作为输入训练模型得到的预测误差,Proposed2是按上文所述方法对起终点附近区域进行截取,然后训练得到的预测误差.从图6中首先可以看出,已知的轨迹长度越长,对目的地位置的预测越精准.当只获取很短一部分轨迹时,他们的目的地可能与其匹配的历史轨迹的目的地相一致,也可能完全不同;然而已知的轨迹段越长,在起点附近的信息和目的地附近的信息提供的信息越多,越有利于对目的地的坐标的确定.此外,将整段轨迹输入模型进行预的效果并不好,其预测误差与按照上文方法处理得到的预测误差相比大很多.

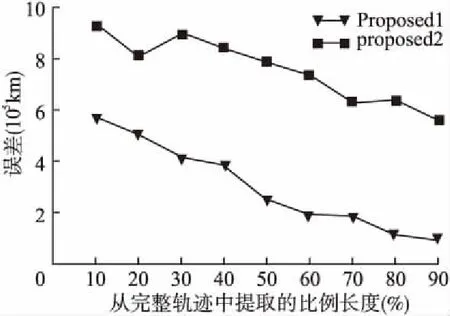
图6 不同完整度的轨迹所对应的预测误差Fig.6 Prediction error given different completeness ratio of trajectories

第二种方法是从测试集中按照随机比例的长度提取轨迹作为测试数据,对他们的目的地进行预测.本文将测试结果与文献[16]中其他模型的预测结果进行对比,对比结果如表3所示.表中各模型的含义分别如下:其中,模型1是在竞赛中取得冠军的模型,其将轨迹前后各5个点的经度和纬度输入一个多层感知机(MLP)中,然后嵌入其他属性,实现对目的地的预测;模型2使用循环神经网络(RNN)模型,依次读取轨迹中所有的GPS点,在每个时间步中,用相同的转换矩阵更新一个固定长度的内部状态,该模型直接通过最后一个内部状态来直接预测目的地;模型3使用了双向RNN,同时正向和反向读取已知的轨迹前缀,得到起点和终点附近的信息,将其输入一个MLP中,随后采取与模型1相同的操作;模型4和模型5都是模型3的变体,前者在每个时间步采用了包含5个连续GPS点的滑动窗口;后者从历史轨迹中提取出部分候选轨迹,将查询轨迹和候选轨迹集都编码成固定长度的向量,通过点乘的方式比较两者之间的相似性并将该值输入Softmax函数,以输出的概率作为每条候选轨迹的终点的权重,从而得到查询轨迹可能的目的地.

表3 不同模型的预测误差对比
Table 3 Prediction error of different models

模型测试误差(105km)1.MLP,clustering(winning model)2.812.RNN3.143.Bidirectional RNN3.014.Bidirectional RNN with window2.605.Memory network2.87Proposed14.62Proposed21.98

Proposed1是将整段轨迹作为输入得到的预测误差.

Proposed2是按照25%的比例截取起点和终点部分轨迹作为输入得到的预测误差.

表3中Proposed1将整段轨迹作为模型输入,进行预测的误差明显高于Proposed2,这再次验证了3.2节中所说的:终点相同的两条轨迹整体相似度并不一定很高,相似度较高的两条轨迹也未必目的地相同.Proposed2的最终预测误差为1.98(105km),实现了最低的预测误差,不论与其他模型还是与冠军模型的2.81(105km)相比,都有很大的提升.这进一步说明了将模型输入从一维轨迹数据转换为二维像素图像的方法是可取的,本文通过引入PDML和PRT方法来克服数据稀疏是非常有效的.

5 结束语

在实现目的地预测时,现有数据集中的历史轨迹数量有限,往往不足以覆盖所要预测轨迹的所有可能,这种现象导致的“数据稀疏问题”会对预测精度造成不良影响.本文通过构建CNN对目的地实现了准确的预测,重点针对预测中的数据稀疏问题提出了相应的解决方法.首先,本文引入PMDL算法,对原始轨迹数据进行最优分段表示,突出轨迹中的重要特征;随后,提出PRT算法,将轨迹在尽可能小尺寸的网格中表示出轨迹序列的像素图片形式;接着,截取轨迹图像的重要特征部位并添加相应的标签,输入CNN进行特征提取和目的地预测.本文在真实轨迹数据集上进行了实验,实现了1.98(105km)的预测误差,与当前先进模型相比有很大的提升.此外,本文所提出的克服数据稀稀疏问题的方法不仅限于对出租车目的地进行预测,为其他诸如动物迁徙、飓风运动等与轨迹数据相关的预测问题也提供了参考价值.

在未来的工作中,将继续研究解决目的地预测中数据稀疏问题的方法,力求实现更精准的目的地预测.