双向循环荷载下的单桩基础累积侧向位移

胡安峰， 肖志荣， 江进华， 付 鹏， 南博文

（1.浙江大学 滨海和城市岩土工程研究中心；软弱土与环境土工教育部重点实验室，杭州310058；2.浙江科技学院 土木与建筑工程学院，杭州310023）

随着经济的不断发展，桩基础在港口码头、跨海大桥等工程中应用越来越广泛，这类桩基础破坏机理和变形情况比传统桩基更为复杂.车辆等交通荷载产生竖向作用，风、波浪等产生水平向作用，而且这些荷载作用为长期循环，使桩基容易产生累积变形.因此，研究竖向和水平循环荷载作用下桩基础的累积侧向位移意义重大.

国内外学者对水平循环荷载作用下桩基变形特性做了大量研究.桩基础侧向变形分析方法最普遍的是美国石油协会（API）[1]建议的p－y曲线分析法，但在水平循环荷载作用下桩基侧向位移分析中，API建议的折减系数不能体现循环次数对累积变形的影响.Poulos[2]在采用p－y曲线法研究桩基循环累积变形时考虑了桩周土体强度和刚度随循环次数衰减的影响，并给出了循环荷载作用下土体强度与刚度弱化因子的计算曲线.Rosquoet等[3]进行了一系列水平循环加载下桩基特性试验，得出了循环荷载大小与桩身循环变形之间的关系表达式.朱斌等[4]进行了砂土中大直径单桩水平受荷试验，提出了与循环应力比相关的p－y曲线循环弱化因子和相应的桩基累积变形分析方法.郭玉樹等[5]提出了通过室内循环三轴试验的结果来分析单桩基础在水平循环荷载下变形的方法.罗如平等[6]通过开发有限元用户子程序将刚度衰减模型嵌入到数值分析中，研究了荷载特性与循环次数对桩基累积水平变形的影响.

港口码头和跨海大桥等工作环境复杂，桩基础同时承受水平和竖向循环荷载作用，但以上研究在分析桩基累积侧向变形时没有考虑竖向循环荷载的影响.Parvin等[7]利用数值模拟和模型试验，分析了水平和竖向循环荷载耦合作用下单桩的特性，表明桩身轴力、桩身弯矩比单向加载时都更大；左殿军等[8]利用数值模拟研究了水平和竖向循环荷载作用下码头群桩基础的受力特性；但两者都没有考虑桩周土体循环弱化发生刚度衰减的特性.本文基于室内循环三轴试验数据，建立考虑双向循环荷载下的软黏土刚度衰减模型，利用商业有限元软件Abaqus进行二次开发，通过用户子程序将刚度衰减模型嵌入到有限元分析中，研究竖向和水平循环荷载耦合作用下单桩基础的累积侧向位移特性.

1 刚度衰减模型

许多学者研究了土体在循环荷载作用下的特性，提出了一些软化模型.Idriss等[9]最早提出了软化指数δ的概念，即土体切变模量在第N次与第1次循环时的比值，建立了软化指数与循环次数关系的表达式：

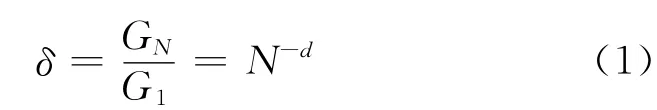
式中：d为软化参数.Yasuhara等[10]在研究砂土循环特性时，提出了软化指数和循环次数之间的半对数表达式：

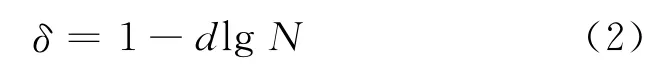
王军等[11]开展了饱和软黏土的循环三轴试验，发现δ与lgN之间并不是简单的线性关系，而是存在较明显的曲线关系，因而提出公式如下：

式中：α，β为软化参数.王军等[12]又研究了双向循环荷载作用下饱和软黏土的软化特性，对土样同时施加径向和轴向正弦循环荷载如图1所示.

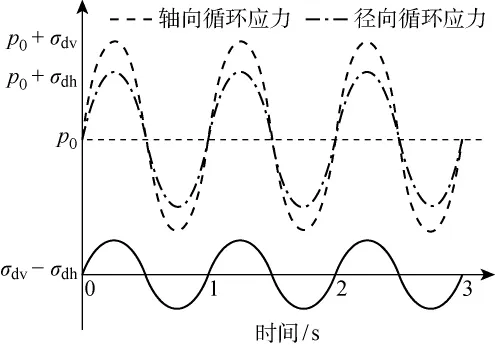
图1 双向正弦循环荷载曲线[12]Fig.1 Bidirectional sinusoidal cyclic loadings[12]

图中p0为围压，σdh与σdv分别为径向与轴向循环应力，循环偏应力σd＝σdv－σdh.为了便于研究，分别定义了循环偏应力比与径向循环应力比：

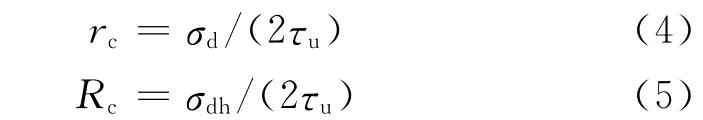
式中：τu为土体不排水强度.文中分析了循环偏应力、径向循环应力对软化参数的影响，考虑双向循环荷载作用下土体的软化情况，利用式（3）建立了软化模型.虽然考虑了rc和Rc对δ的影响，但模型公式复杂，拟合参数较多，难以确定，在实际工程中应用难度较大.

基于此，本文在其试验数据基础上对软化参数α和β进行重新拟合，得到较简洁实用的关系式如下，从而改进软化模型.

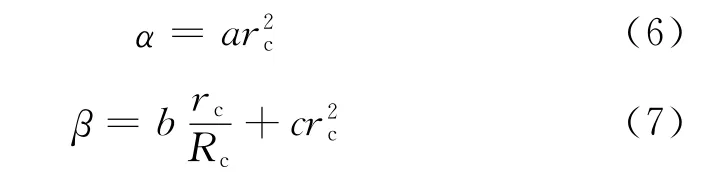
式中：a，b，c均为拟 合 参 数，分 别 为0.010 34，－0.044 52，0.485 21.图2所示为修正刚度衰减模型与实测数据的对比.从图中可以看出，修正刚度衰减模型曲线与实测数据点吻合得较好，发展变化趋势相同，进一步说明了本文刚度衰减模型的正确性.

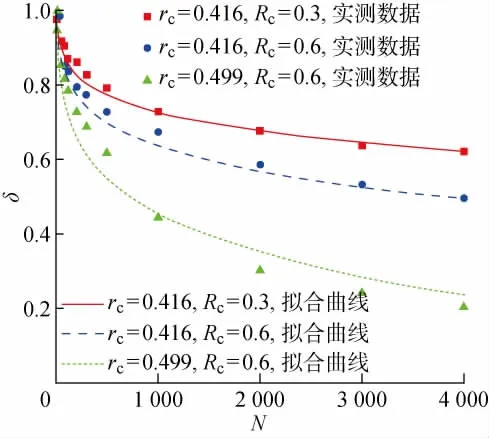
图2 修正刚度衰减模型Fig.2 Modified model of stiffness degradation

2 数值模拟

2.1 建立模型

在桩土模型中，饱和软黏土地基采用 Mohr－Coulomb弹塑性模型，参照文献[13]可得相应参数.桩体材料为混凝土，桩基采用线弹性模型，土体及桩基模型参数如表1所示.

通过有限元软件Abaqus建立三维桩土有限元模型.由于模型及受力的对称性，桩土模型采用半圆柱体.图3所示为数值计算模型，单桩直径D＝1m、桩长L＝20m，为了避免模型边界条件对数值模拟结果的影响，桩基中心距水平向边界和桩底距地基底部的距离都取15倍桩径[14]，桩土之间建立摩擦接触，摩擦因数为tan（0.75φ）.受荷时桩土模型如图4所示.其中，y为桩顶侧向位移，Fh与Fv分别为水平循环荷载和竖向循环荷载.

表1 土体及桩基模型参数Tab.1 Model parameters of soil and pile

图3 桩土数值计算模型Fig.3 Numerical simulation pile－soil model

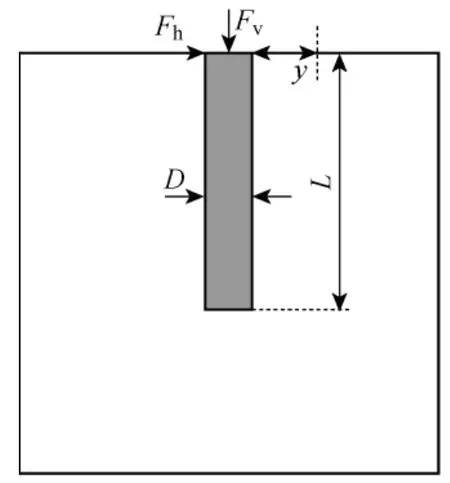
图4 受荷时桩土模型剖面图Fig.4 Profile of pile－soil model under loadings

2.2 刚度衰减模型的实现

建立桩土模型，进行地应力平衡后同时对单桩施加水平循环荷载和竖向循环荷载.要在有限元分析中实现刚度衰减模型，需执行以下3个步骤.

（1）输出施加循环荷载前后每个土体单元的最大主应力和最小主应力，即σ（1）1、σ（1）3与σ（2）1、σ（2）3.

（2）计算出σ（2）1与σ（1）1和σ（2）3与σ（1）3的差值，即分别得到σdv和σdh；然后算出循环偏应力σd.

（3）由σd和σdh根据式（4）和（5）求得每个土体单元所受的循环偏应力比与径向循环应力比，再依次利用式（6）、（7）和（3）计算所有土体单元在双向循环荷载作用下的软化指数，最后通过子程序来实现土体刚度衰减模型在有限元分析中的应用.

3 有限元模型的验证

Liao等[15]在近海软黏土中开展了不同水平循环荷载作用下PVC管桩侧向位移发展的室内模型试验.在模型试验中，桩长1 000mm，嵌入深度700 mm，桩径为50mm，壁厚5mm，黏土重度为17kN／m3，模型桩的水平静力极限荷载为100N.采用本文的方法，建立和模型试验参数一致的有限元模型，计算单桩在不同水平循环荷载下的累积侧向位移，再和模型试验结果比较，如图5所示.从图中可以看出，在水平循环荷载作用下，本文结果比原试验略小一些，但发展变化的规律相同.同时，在N＝1 000后，侧向位移发展趋于平稳.这表明本文提出的刚度衰减模型可用于研究软黏土中单桩基础的侧向位移问题.

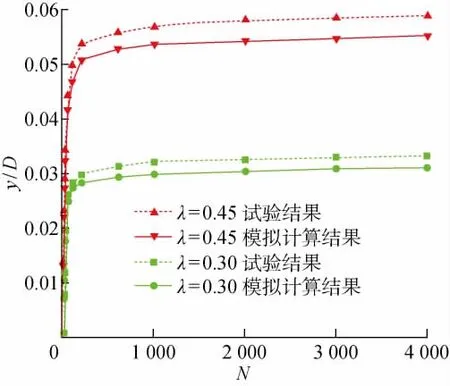
图5 本文模拟与模型试验结果对比Fig.5 Comparison between the proposed model and model test

4 双向循环荷载下桩基侧向位移分析

研究双向循环荷载作用下桩基侧向位移，需要先确定桩基的水平极限承载力Fhu和竖向极限承载力Fvu.参考Zdravkovi＇c等[16]研究方法，基于桩顶水平变形0.1D来确定Fhu，根据建筑桩基技术规范[17]可以确定Fvu.为模拟双向循环荷载作用下单桩基础受力状态，在竖向和水平向同时施加正弦规律变化的循环荷载如下.

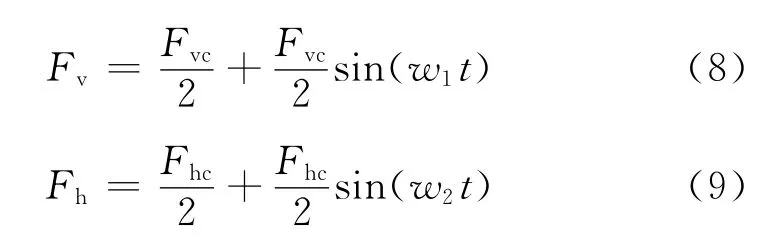
式中：w1，w2代表荷载频率；t为加载时间；Fvc，Fhc分别是竖向循环荷载幅值和水平循环荷载幅值.借鉴既往研究方法[18－19]，取w1＝w2＝1Hz，定义竖向循环荷载比η＝Fvc／Fvu，水平循环荷载比λ＝Fhc／Fhu.取不同的循环荷载比，进行不同幅值循环荷载作用下单桩基础累积侧向位移研究：η＝0.1，0.2，0.3，0.4，0.5；λ＝0.1，0.2，0.3，0.4，0.5，0.6.

4.1 双向循环荷载下桩顶侧向位移的发展

竖向循环荷载幅值恒定（η＝0.2）时，改变水平循环荷载幅值，桩顶累积侧向位移的发展情况如图6所示.从图中可以看出，当水平循环荷载较小时（λ＝0.1）侧向位移基本保持不变，累积位移不足0.01m.由此可知存在最小水平循环荷载比λmin，当λ≤λmin时侧向位移并不随着循环次数增大而累积.当λ从0.2到0.5时，侧向位移随循环次数增大而迅速发展，在N＝1 000后发展变缓，最后趋于稳定.因此，水平循环荷载产生的循环效应主要集中在循环周期的前面阶段，朱斌等[4]在砂土模型试验中也得到类似规律.当λ＞0.5时，桩顶侧向位移随着循环次数急剧增大，桩顶侧向位移并不趋于平稳.基于此，表明存在最大水平循环荷载比λmax，从控制变形的角度分析，λ应控制在0.5以下.

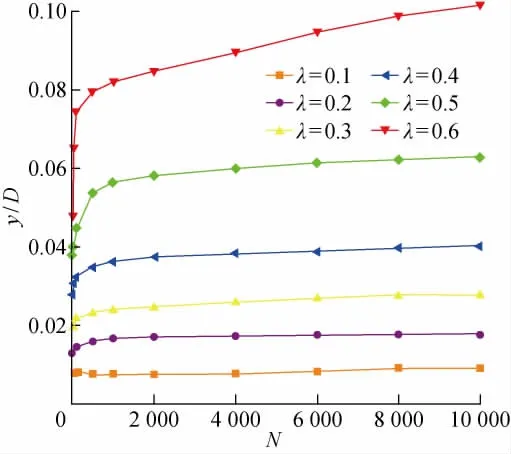
图6 不同水平循环荷载下的桩顶侧向位移Fig.6 Lateral displacements of pile head under various lateral cyclic loadings

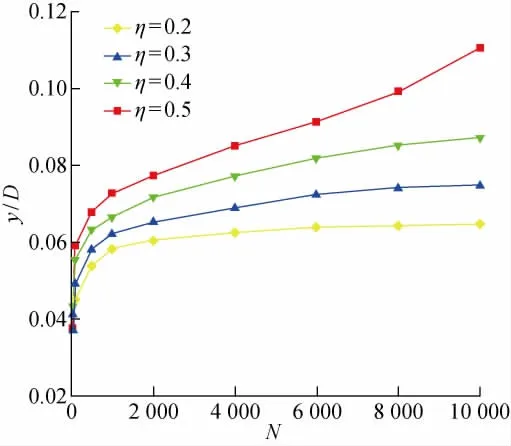
图7 不同竖向循环荷载下时桩顶侧向位移Fig.7 Lateral displacements of pile head under various vertical cyclic loadings

图7所示当λ＝0.5时，不同竖向循环荷载下桩顶累积侧向位移的发展情况.如图所示：η为0.2和0.3时桩顶侧向位移开始时增长较快，后期逐渐趋于平稳；同时随着η增大，桩顶侧向位移的发展速度增快，而且达到稳定时所需要的循环次数也越大.例如η＝0.2时，位移趋于稳定需要约1 000次，然而η＝0.4时，循环1 000次后累积位移仍持续增长，与图6中水平循环荷载作用下N＝1 000后位移趋于平稳有所不同，说明竖向循环荷载影响桩顶侧向位移的发展，推迟其平稳阶段.当η＝0.5时，桩顶位移持续增大，y／D超过0.1时桩基已经被破坏.因此，当竖向与水平循环荷载都比较大时（λ＝0.5，η＝0.5），桩基础累积位移发展迅速，位移值较大，桩基容易破坏，在实际工程中应避免双向循环荷载都较大的情况.

双向循环荷载作用下桩顶累积侧向位移如图8所示（N＝10 000）.当水平循环荷载较小时（λ＝0.1），桩顶侧向位移很小且几乎不变，说明水平循环荷载较小时竖向循环荷载的增大对桩顶侧向位移影响很小.当水平循环荷载较大时（λ为0.2～0.5），随着η增大，桩顶侧向位移不断增长，而且发展速度加快.竖向循环荷载比η从0.1到0.2时，桩顶侧向位移增长较小，但η为0.2～0.5时，桩顶侧向位移增长迅速，这说明竖向循环荷载比对桩基累积变形的影响存在一个界限值ηlim.朱斌等[19]在砂土中竖向循环受荷单桩的沉降模试型验中也发现类似规律.验证了本结论的正确性.

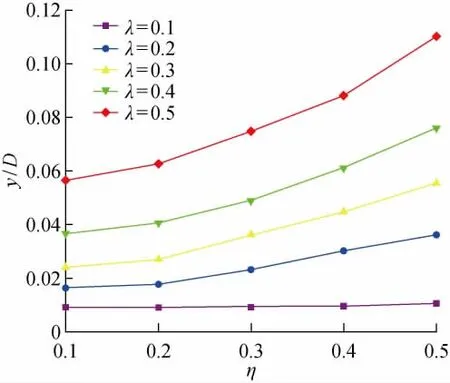
图8 双向循环荷载下的桩顶侧向位移Fig.8 Lateral displacements of pile head under bidirectional cyclic loadings

4.2 单向与双向循环荷载下桩顶侧向位移的对比

N＝10 000次时，桩顶施加竖向静载（0.3Fvu）与竖向循环荷载（η＝0.3）下的桩顶累积侧向位移对比情况如图9所示.由图可见，当水平循环荷载较小时，两者位移相近，当水平循环荷载较大时，竖向静载条件下的侧向位移明显小于竖向循环荷载条件下的侧向位移，且差距不断增大.这是因为单桩受到双向循环荷载耦合作用时，桩周土双向受荷，双向循环荷载作用下土体的强度比单向循环荷载作用下强度低[20].循环荷载较小时，应变发展缓慢，土体的应变较小，土体内部结构尚未破坏，故而两者桩顶侧向位移相近.循环荷载增大时，双向受荷土体的应变迅速发展，土体内部结构较早开始被破坏，出现应变软化现象，刚度不断减小，故而桩基变形更大.

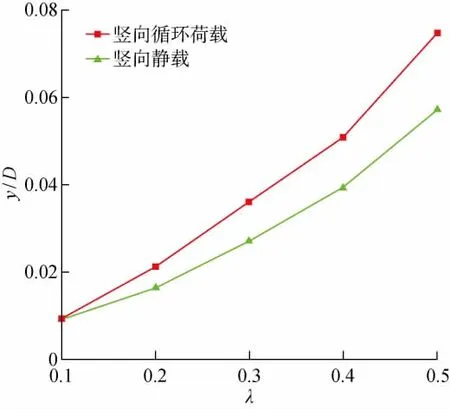
图9 竖向静载与竖向循环荷载下的桩顶侧向位移Fig.9 Lateral displacements of pile head under vertical static and cyclic loadings

4.3 不同竖向循环荷载下的桩身侧向位移

不同竖向循环荷载下桩身侧向位移的发展情况如图10所示（λ＝0.3，N＝10 000），其中z为桩基的竖向坐标.可以看出，η为0.1和0.2时，位移零点的位置在埋入深度为10m左右，之后随着η的增大，位移零点的位置不断下移，说明竖向循环荷载的增大加深了桩土变形的区域.同时，桩身侧向位移也随着η的增大而不断发展，η＝0.1和0.2时，位移曲线基本重合，而η＝0.3的零点以上侧移比η＝0.2的零点以上侧移发展更迅速，说明竖向循环荷载对桩基变形的影响存在一个界限值.

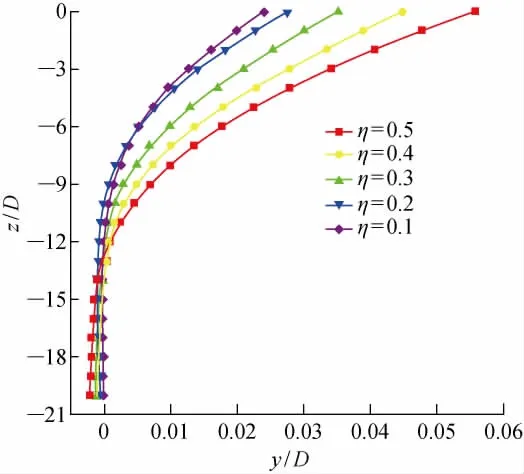
图10 不同竖向循环荷载作用下的桩身侧移Fig.10 Lateral displacements of pile under various vertical cyclic loadings

5 结语

本文建立了基于双向循环受荷的软黏土刚度衰减模型，通过用户子程序将刚度衰减模型嵌入到有限元模型分析中，研究竖向和水平循环荷载耦合作用下单桩基础的累积侧向位移特性，得到如下结论：

（1）水平和竖向循环荷载耦合作用下，桩周土体双向受荷，应变发展迅速，刚度不断减小，易出现应变软化现象，使得桩顶侧向位移相比于只受水平循环荷载下的位移更大.循环加载一定周期后，桩顶累积侧向位移逐渐趋于平稳，但竖向循环荷载的增大会推迟其平稳阶段，使其达到平稳阶段的循环周期增大.

（2）水平循环荷载比存在临界值λmin和λmax.当λ≤λmin时，桩顶侧向位移不会随着循环加载而累积.当λmin＜λ≤λmax时，循环加载前期桩顶累积侧向位移随着循环次数增大而增大，后期逐渐趋于平稳.当λ＞λmax时，桩顶累积侧向位移迅速增长，后期并不趋于平稳.

（3）当水平循环荷载较小时，竖向循环荷载对桩顶累积侧向位移影响不大.当水平循环荷载较大时，竖向循环荷载对累积侧向位移的影响存在一个界限值，即ηlim.竖向循环荷载比小于该值时，竖向循环荷载对累积侧向位移影响很小.