基于改进质量源造波方法的非线性波数值模拟
2020-01-14孙家文房克照翟钢军
马 哲, 周 婷, 孙家文, 房克照, 翟钢军
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连116024;2.大连理工大学 深海工程研究中心,辽宁 大连116024;3.国家海洋环境监测中心,辽宁 大连116023)
基于计算流体力学(CFD)的数值造波方法是海洋工程领域的研究热点,常用的有推板造波法、速度入口法和源造波法.文献[1]基于速度入口法实现了二阶Stokes的数值模拟.文献[2-3]针对推板造波方法开展了相关研究,成功模拟了线性波和瞬时极限波.源造波法根据源项添加位置的不同可分为质量源和动量源两种[4-5],作为一种新型造波方法,因能充分利用数值模拟的优势而受到越来越多的关注.以往研究[5]表明,质量源造波较动量源法适用的水深范围更广,且可以实现线性波和非线性波等不同目标波浪的模拟,但源区形状会对目标波浪的模拟产生明显影响.文献[6]通过试算得出质量源造波源区的长度和宽度只有满足特定条件时才能达到比较理想的模拟效果;文献[7]在内域造波中通过多组波况的模拟分析拟合得到质量源长度和宽度的经验公式;文献[8]采用水平形式的质量源,考虑垂向质量输出,模拟了孤立波的行进过程;同样对孤立波传播进行数值模拟,文献[9]选择了垂向造波源,并指出以一个网格的水平长度Δx作为源区宽度可保证波浪模拟的精确性.然而,采用质量源进行数值造波得到的波高幅值往往小于理论值,仅仅依靠调节质量源的长度和宽度对模拟效果的改善存在局限性.文献[10]认为质量源在造波过程中的部分能量未能发挥作用,可以通过在源项表达式中乘一个放大系数以弥补损失的能量;文献[11]针对浅水情况,在源强方程中考虑了垂向源区上方的质量输出,避免了造波过程中源区上方水体高度值多次试算带来的不便.
为了改善质量源造波的效果,上述文献均对质量源形状进行了限制.质量源形状影响造波的主要原因是推导源强方程时没有完整地考虑质量输出在各个方向对造波所做的贡献,从而导致在一些情况下模拟值较理论解偏小.尤其在长宽比不满足条件时,仅考虑单方向质量输出不能满足精度要求,因此才有了使源项强度线性增大来弥补波能损失这一措施,但对于不同的波况,源强增大倍数也各有不同,每次都需要试算来确定显然费时费力.
基于上述问题,本文提出了一种无需限制源区形状的改进方法.首先从理论分析的角度,揭示了传统质量源造波法非线性波模拟出现波幅偏小的原因,在此基础上修改源项方程,针对矩形质量源,充分考虑源区质量输出在各个方向对造波所做的贡献,得到了新的质量输出的源项函数.然后,利用改进方法模拟了不同相对水深、不同非线性条件下的Stokes二阶波和孤立波.在本文的模拟过程中,改进方法不依赖于源区形状的长宽比,因此对于不同的波况无需多次进行源区形状的调试工作,大大提高了工作效率.
1 数值模型
1.1 控制方程与数值求解方法
数值模型基于开源CFD类库OpenFOAM中不可压缩气液二相流求解器interFoam[12],采用Volume of Fluid(VOF)方法[13-14]进行自由面的捕捉,控制方程为连续性方程、引入相体积分数α的动量方程以及VOF方程:

式中:u为平均速度;t为时间;ρτ为雷诺应力项,其中τ表征由于Δ脉动值引起的雷诺应力张量,为二阶对称张量;Cκα为表面张力项,C为表面张力系数,一般取0.07kg/s2,κ为自由面曲率;g为重力加速度;X为位置矢量;ur代表相对速度,含有ur的项为人工压缩项[15],只在二相交界面处起作用.ρ和μ分别为二相流的平均密度和平均动力黏度:
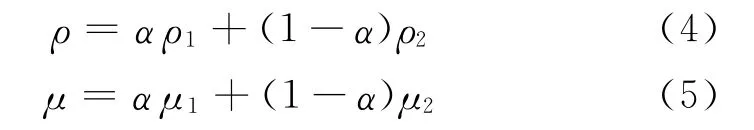
对控制方程的求解需要对时间和空间进行离散,OpenFOAM采用有限体积法离散框架,时间积分项采用隐式欧拉格式,体积分中的对流项采用Guass limitedLinearV 1格式离散,黏性扩散项采用linear corrected,其余用线性插值.速度压力场采用分离式(segregated)算法PISO.离散后的线性方程组采用预处理共轭梯度法求解.
1.2 改进的质量源造波理论推导
为了实现质量源造波,需要在造波源区对式(1)添加源项,如下所示.
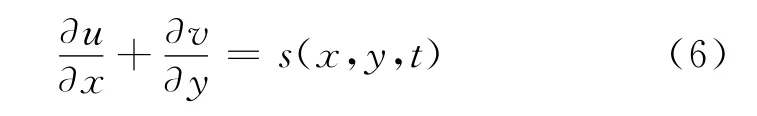
式中:u和v分别是质量源区内质点的水平和垂向速度;x和y为位置,s(x,y,t)为质量源源强.不同的目标波浪对应不同的源强表达式,其推导过程如下:
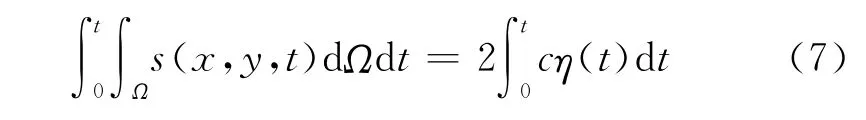
式中:c为目标波浪的相速度;η(t)为自由表面方程;Ω为质量源所在的区域.式(7)的意义为在某一时间段内,质量源区质量的输出用于产生目标波浪[16].右端系数2表示质量源区的质量输入向左右两边都产生了波浪.简化式(7)可得
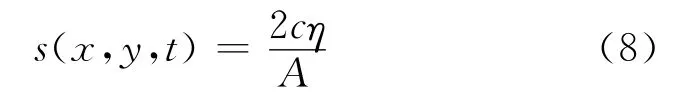
式中:A为质量源区的面积.
上述推导过程考虑了质量源在相速度方向的质量输出,忽略了垂向,而实际上源区的质量输出在4个方向同时存在.基于此,本文进行了如下改进.
在质量源区,假设每个网格应该满足以下关系:
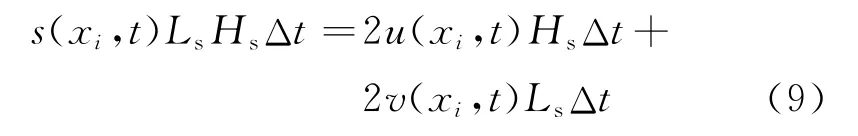
式中:Ls和Hs分别是质量源的长和宽.对式(9)进行化简可得
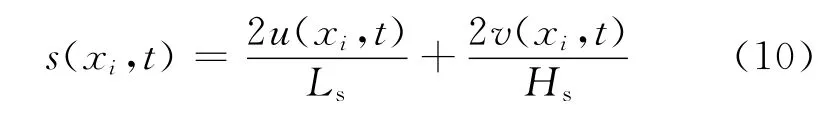
根据文献[17],质量源造波在原理上类似于水下爆炸,爆炸瞬间质点向各个方向的运动速度相同,质量源向外输出流体沿各方向的速度也相等,即u=v.最终源强简化为
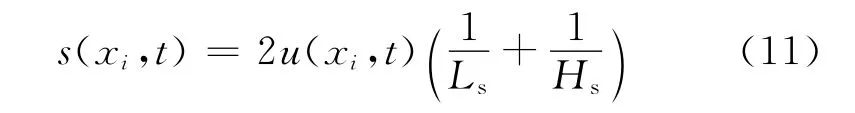
为了保证数值的稳定性,源强函数的初始值应为0.在源强中添加缓启动因子(SSF),定义在很短的初始时间段t0内,源强函数的值从0开始增加,具体表达如下:
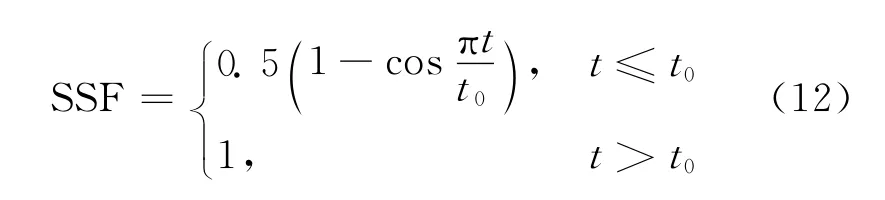
最终,源强的表达式为
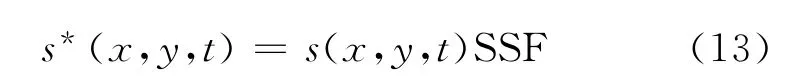
由式(11)可见:当Ls和Hs不在同等量级时,以横向质量源(Ls≫Hs)为例,此时可以忽略式(10)右端第一项,仅需要考虑质量源区垂向方向质量输出就能满足造波的精度,所以利用式(8)推导出的质量源源项在横向质量源中可以取得较好模拟结果;同理,竖向质量源(Ls≪Hs)只需考虑横向质量输出也能达到数值造波的精度要求.但当质量源的长宽比介于0.1~10时,只考虑单方向质量输出时得到的数值结果普遍较差,因为这种近似本身存在理论上的缺陷,需要对质量源形状限制来弥补.式(11)考虑了质量源区4个方向的质量输出,其造波精度不依赖于矩形源区的形状变化,提高了源区形状变化的灵活性.
1.3 消波方法
为了防止波浪反射对模拟效果的影响,本文在数值水槽的左右两端分别添加阻尼层.常用的阻尼消波方式有指数、线性、根号、平方等形式,合理选择消波函数会对反射率产生影响[18].本文算例均采用线性阻尼消波形式,衰减系数取8,可取得较好的消波效果.
2 Stokes二阶波的数值模拟
以二维情形为例进行模拟,数值波浪水槽总长8.46m,高0.26m,水深0.2m,水槽左右两端和底端为固壁边界类型,上端为压力出口边界.质量源区位于水槽中间,根据文献[6]源区位置设置经验法则,源区中心距静水面的距离设为1/3水深,阻尼消波段首尾各为1.21m,如图1所示.
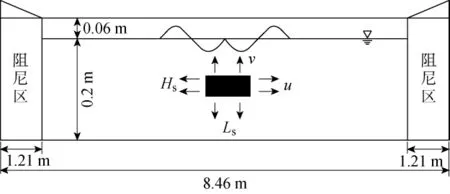
图1 二维数值水槽示意图Fig.1 Diagram of 2Dnumerical wave tank
Stokes二阶波的自由表面函数为
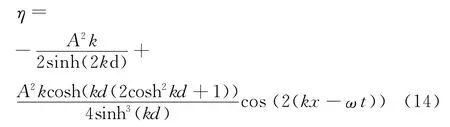
式中:k为波数;d为水深;ω为圆频率.将式(14)代入式(12),得到Stokes二阶波的质量源源强表达式.
2.1 网格、时间步长对造波效果的影响
既往研究[2]表明,网格和时间步长尺度选取带来的数值黏性对数值水槽的模拟效果具有重要影响.以Stokes二阶波为例,水深d=0.2m,波高H=0.04m,并定义无量纲参数ε表示波浪的非线性(ε=H/d).分别选取3组不同网格大小和4组不同时间步长的工况,对数值模拟结果的影响进行比较分析.
3组不同网格的设置和模拟结果如表1所示(其中T为波浪周期),横向网格始终保持为0.012 m,可见加密垂向网格有利于数值模拟精度的提高.从算例M1到算例M2,数值模拟波幅与理论值的误差明显减小.从算例M2到算例M3,网格数量翻倍,但误差结果相差不大.模拟结果证明1个波高内有10个网格时可实现理想的造波精度,因此采用0.004m作为垂向网格的长度.

表1 网格的验证Tab.1 Verification of mesh
4组不同时间步长的设置和模拟结果如表2所示,时间步长对数值模拟的影响程度不大,当时间步长取0.02s时,模拟结果与理论值的误差为3.15%,满足精度要求.算例T1和T2时间步长分别取0.002和0.001s,同算例T3相比,误差改善效果不明显,但是计算时间大大增加.综合考虑后,选取时间步长为0.02s,即为0.02T时,计算代价最小.
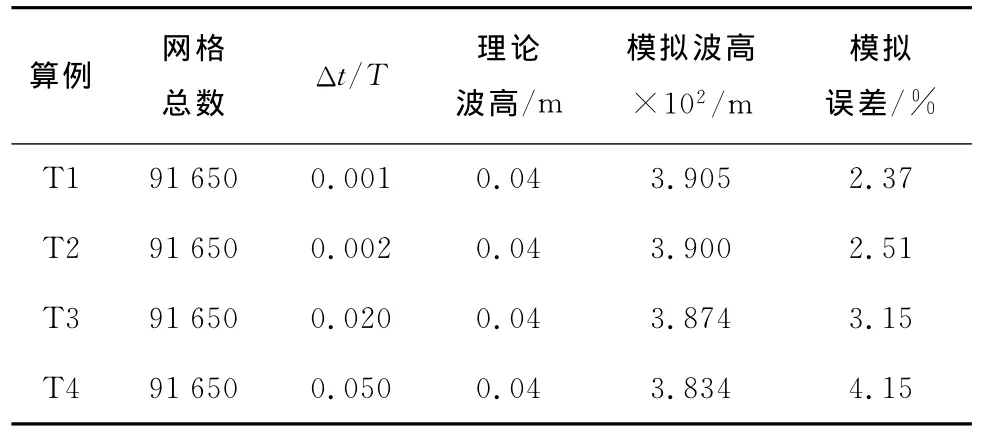
表2 时间步长的验证Tab.2 Verification of time step effects
2.2 不同波高时二阶Stokes波的模拟
数值造波对非线性参数ε要求相对比较苛刻,对于非线性较强的波浪,往往模拟效果不理想[19].为了检验改进后质量源造波方法的可行性和适用范围,本文探究了相同水深下不同波高时Stokes二阶波的模拟效果.设置时间步长为0.02s,网格0.004 m,d=0.2m,T=1s,H=0.01,0.04,0.05m,相应ε=0.05,0.2,0.25.距离源区中心1倍波长处的自由液面高度随时间的变化过程以及与理论值对比如图2~4所示.
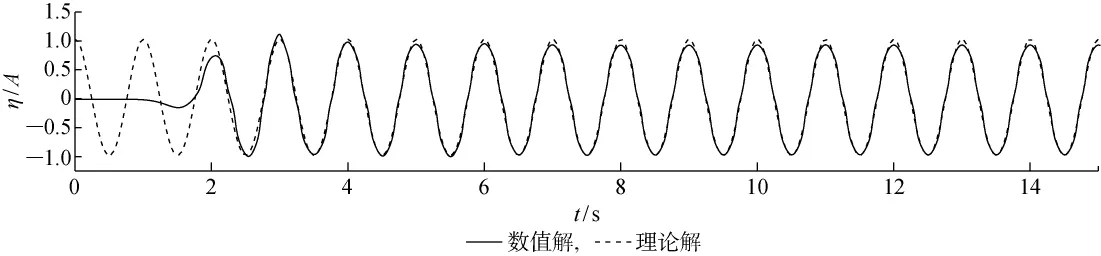
图2 ε=0.05时数值解和理论解的对比 (H=0.01m)Fig.2 Comparison of numerical results and theoretical analysis(H=0.01m,ε=0.05)
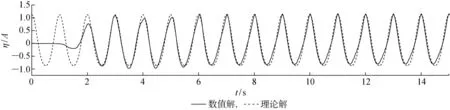
图3 ε=0.2时数值解和理论解的对比 (H=0.04m)Fig.3 Comparison of numerical results and theoretical analysis(H=0.04m,ε=0.2)
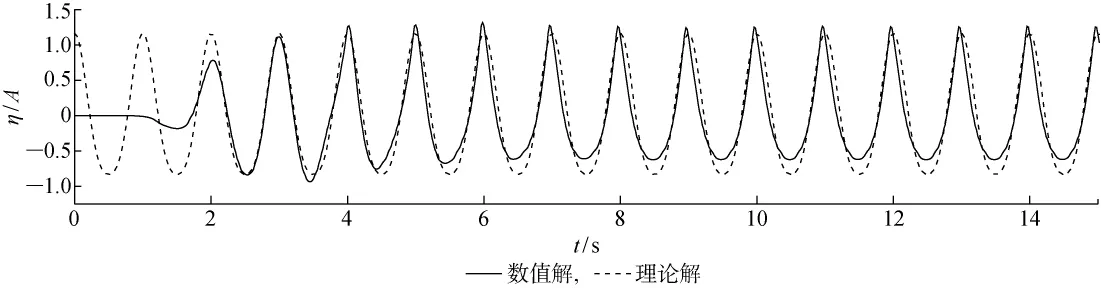
图4 ε=0.25时数值解和理论解的对比 (H=0.05m)Fig.4 Comparison of numerical results and theoretical analysis(H=0.05m,ε=0.25)
由图可见,ε=0.05,0.2时,本文方法模拟效果比较理想.虽然波谷处与理论波面存在微小误差,但仍在精度范围内,波峰与理论波面吻合很好,整个波形的模拟效果非常理想.当H/d=0.25时,波谷处数值解与理论波形的偏差增大,且整个波形有上漂趋势.因此,本文方法对于ε=0.05~0.2的Stokes二阶波模拟效果较好.
2.3 数值模拟精度的改善
ε为衡量数值水槽造波能力的重要参数,为了验证本文方法对造波效果的改善作用,以ε大小为标准与前人模拟结果进行了比较.文献[20]基于质量源造波方法对Stokes二阶波进行了数值模拟,波浪参数中H=0.1m,d=1.8m,文献[6]利用质量源造波方法模拟Stokes二阶波,在源强推导中考虑了水平方向质量输出,选取H/d为0.2和0.3.针对3种不同ε值,本文的数值模拟结果与文献进行对比,结果如图5~7和表3所示.
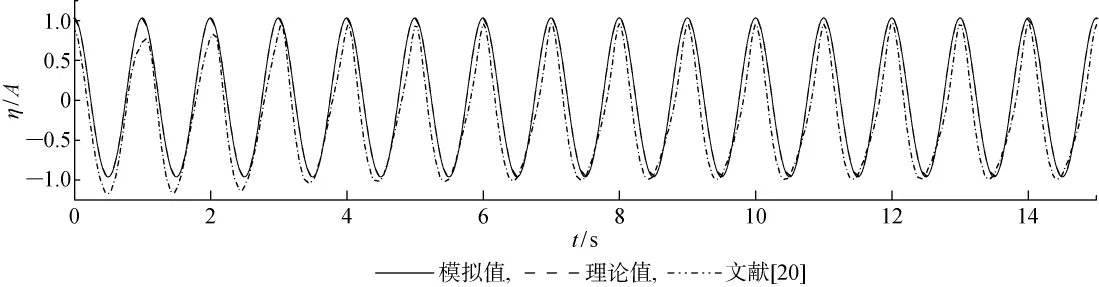
图5 二阶Stokes波时历曲线 (ε=0.05)Fig.5 Time history of second-order Stokes(ε=0.05)
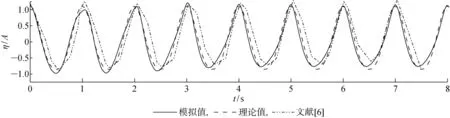
图6 二阶Stokes波时历曲线 (ε=0.2)Fig.6 Time history of second-order Stokes(ε=0.2)
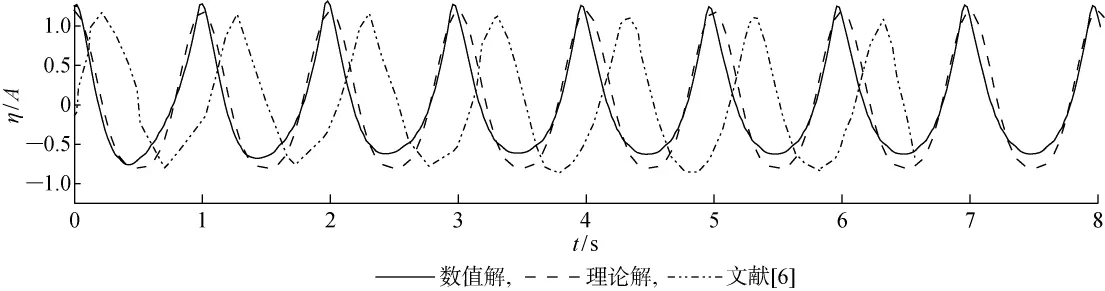
图7 二阶Stokes波时历曲线 (ε=0.3)Fig.7 Time history of second-order Stokes(ε=0.3)
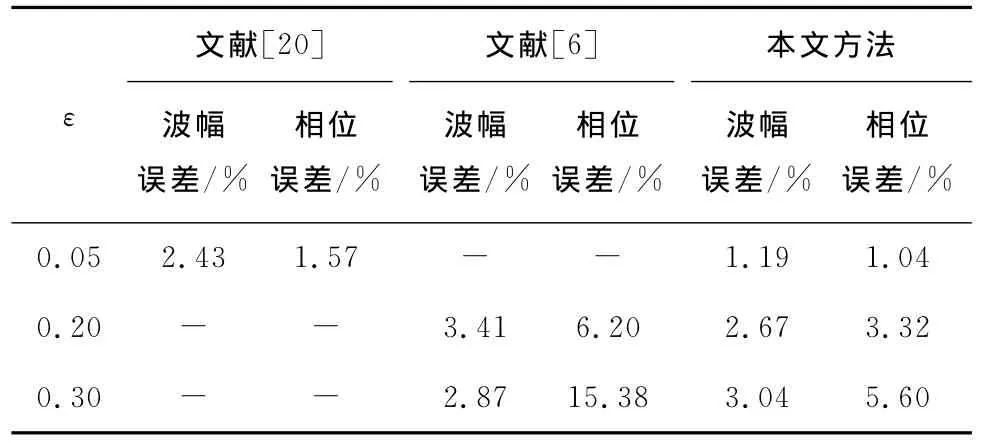
表3 数值误差对比Table 3 Comparison of numerical errors
由表3可见:本文改进后的方法在ε=0.05~0.20时,对波幅误差有较好的改善效果;尤其在ε=0.20时,波幅误差及相位误差相对于传统质量源造波方法分别降低21.7%和46.5%;当ε=0.30时,波幅误差与文献中模拟方法相比结果接近,但相位误差减小了63.6%.
2.4 不同相对水深时二阶Stokes波的模拟
同前人工作类似,文献[7]通过设置多组波况拟合得到源区宽度的经验公式,不同的相对水深(kd)代入经验公式可得到不同的源区宽度,而本文在介绍改进的质量源源项推导过程时,发现改进方法的造波效果不依赖于源区形状.为了探究这一结论的正确性,本文设置4组波况,选取H=0.01m,d=0.2m (ε=0.05),T=1.0,1.5,2.0,3.0s,则距离源区中心1倍波长处的自由液面高度随时间的变化过程与理论值对比如图8所示.
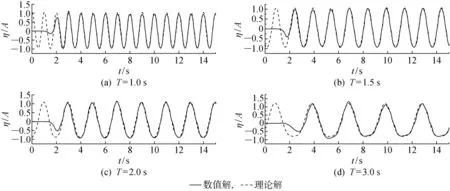
图8 不同周期时数值解和理论解的对比Fig.8 Comparison of numerical results and theoretical analysis with different periods
由图8可知,改进的质量源造波方法在相对水深为0.30~1.08均适用,无需严格按照经验公式[7]计算源区宽度,这证实本文方法不仅降低了造波时对源区形状的限制,并且能取得较好的模拟效果.
3 孤立波传播的数值模拟
为了验证本文方法的实用性,利用改进后的质量源方法对孤立波的传播进行模拟.孤立波的自由表面方程如下:
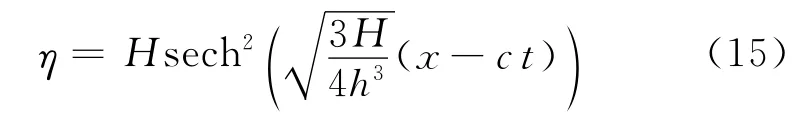
将其代入式(12)即可得到孤立波对应的源强表达式.
3.1 单个孤立波的传播模拟
孤立波为一种浅水波,有其独特性.数值水槽尺寸如图9所示.时间步长为0.001s,水平网格边长为0.02m,垂向网格边长为0.01m.
左右两列孤立波W1和W2为镜像对称,因此选取任意1列作为研究对象即可.图10展示了不同时刻下W2的波面图,H=0.005m,将模拟结果无因次化,可见孤立波在传播过程中波形稳定且振幅衰减小.
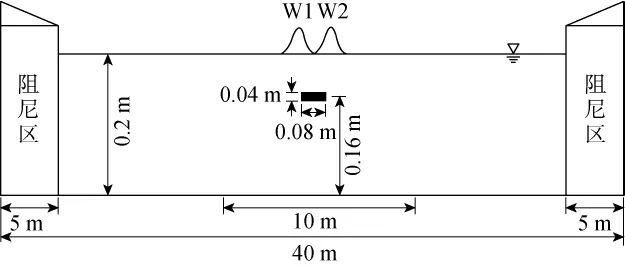
图9 单源数值水槽示意图Fig.9 Diagram of a single-source numerical wave tank
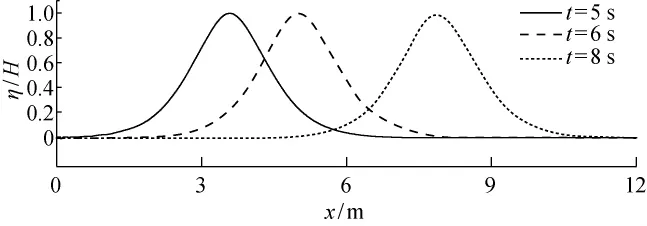
图10 不同时刻下孤立波的波面Fig.10 Wave surface elevation of solitary waves
图11分别展示了在d=0.2m,t=5s时H=0.005,0.01,0.04,0.05m的孤立波波面曲线.由图11可见,3种不同波高情况下基于本文方法得到的波面与理论解吻合很好,随着ε的增大,波峰处误差逐渐增大,主要是由于两列孤立波中间出现了扰动,导致一部分能量损失,并且随着ε值的增大,扰动出现了增大趋势.分析发现,ε达到0.2时,模拟精度在可接受范围内.
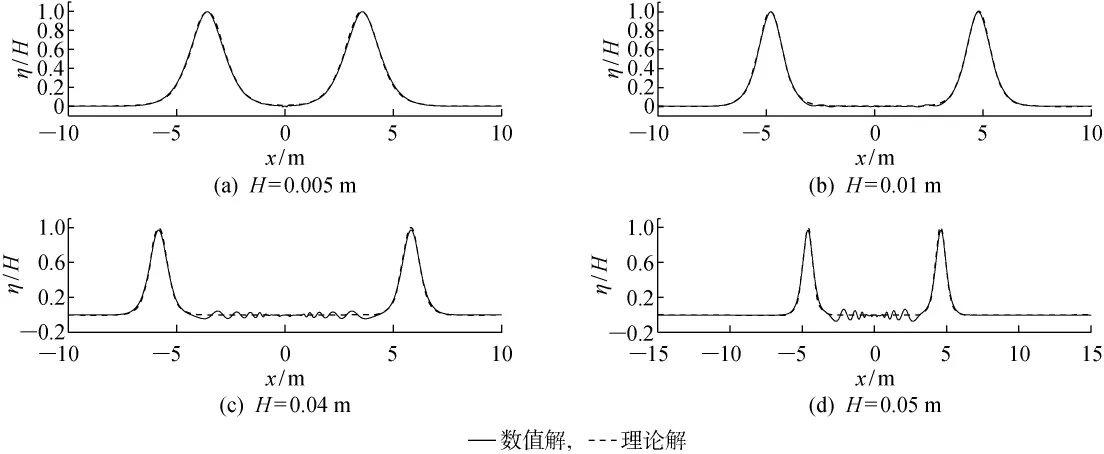
图11 不同波高时孤立波的数值解与理论解的对比 (t=5s)Fig.11 Comparison between numerical results and theoretical analysis with different wave heights(t=5s)
3.2 孤立波“碰撞”过程的数值模拟
为了检验本文方法的有效性,选取两列孤立波相向运动及“碰撞”后演化过程作为数值算例.为了产生两列相向运动的孤立波,在水槽中设置2个质量源区,数值水槽尺寸如图12所示.
左右设置的2个质量源区S1和S2都产生了沿左右传播的孤立波,左侧S1产生的波标记为L1,L2,右侧S2产生的波标记为R1,R2.图13给出了孤立波产生和传播的过程.当t=5s时,S1和S2分别产生两列孤立波,在t=6s时,L2和R1刚好重叠,此时能量达到最大.
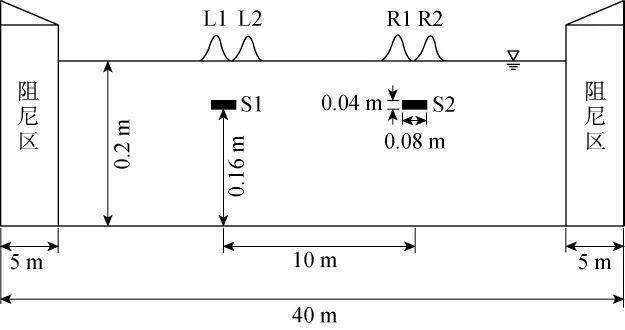
图12 水槽布置示意图Fig.12 Layout of the numerical wave tank
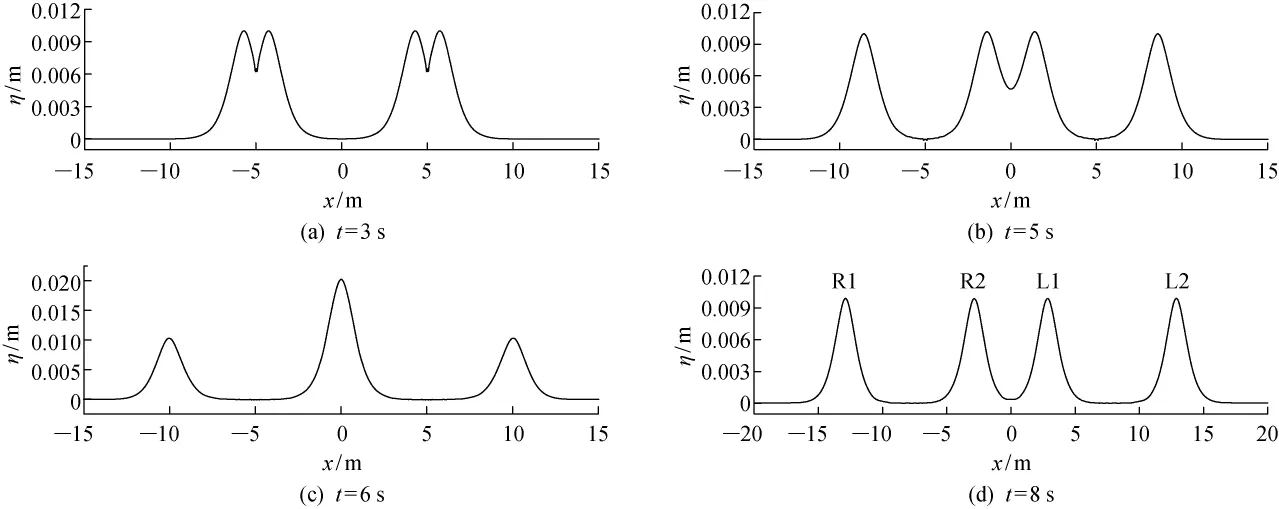
图13 孤立波碰撞过程中不同时刻下的波面图Fig.13 Wave surface elevation at different time during the process of collisions in solitary waves
文献[21]通过理论推导,得出孤立波叠加的理论最大波高计算公式为
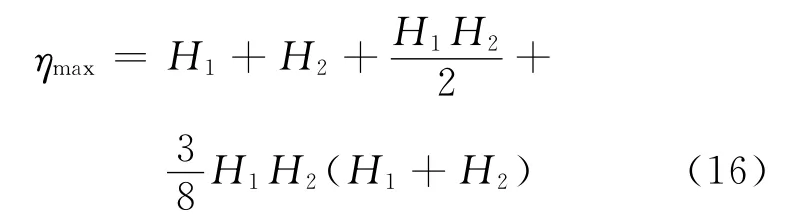
式中:右侧第3项和第4项分别为2阶和3阶小量,在此忽略其量纲的贡献.本文取H1和H2都为0.01m,计算得到理论最大波高为0.020 05m,数值解和理论解的误差小于1%.因此本文方法同样适用于孤立波“碰撞”过程模拟.
4 结语
本文针对传统质量源造波法对强非线性波模拟效果不佳的问题,考虑双向质量输出,提出改进方法.通过理论分析与推导得出新的质量源源项函数,利用该源项公式对Stokes二阶波、孤立波传播过程进行数值模拟,计算结果表明:
(1)质量源对于垂向网格尺寸比较敏感,1个波高内含10个网格时模拟效果较好;时间步长越短,数值黏性越小,取时间步长为0.02T时,在保证造波精度的前提下减少了计算代价.
(2)本文方法避免了对质量源区形状的过多限制(传统线形造波源长宽比小于0.1或大于10),省去了源区形状调试工作,提高了工作效率.
(3)本文方法提高了对强非线性波浪的模拟精度,对于H/d=0.05~0.3的Stokes二阶波取得很好的模拟效果;尤其在H/d=0.2时,波幅误差及相位误差相对于传统方法分别降低21.7%和46.5%.
(4)对于H/d=0.025~0.25的孤立波,本文方法的数值解与理论解吻合很好,并且同样适用于孤立波碰撞叠加过程的模拟.
围绕质量源造波的相关问题还需要进一步开展相关研究,如改善质量源造波在强非线性范围的造波精度;参照前人的工作,将质量源造波方法与动量源造波方法进行比较和分析;在现有二维算例的基础上,拓展三维质量源造波方法,并开展斜向波的数值模拟.
