基于超宽带技术的强制戒毒人员实时定位系统

（上海交通大学 电子信息与电气工程学院，上海200240）

毒品是一种能够使人形成瘾癖的精神麻醉药品.成瘾者易产生抑郁、狂躁、精神分裂等症状，严重威胁自身及公共安全[1].为及早预防疾病、及时处理意外事件，对戒毒所内人员的生理和行为的实时监控显得尤为重要.

早期的监控依靠视频监控以及人工巡视的方法，需要大量人力，难以保证及时性且容易漏检.伴随着物联网（IOT）技术和人工智能（AI）技术的发展，采用无线方式的生理参数监控和定位成为研究热点[2].目前在康复监护领域的诸多研究中，基于无线传感网络（WSN）方法的生理参数测量技术已经日趋成熟[3－4]，但对强制戒毒人员实时定位的研究较少，且定位精度低一直是个亟待解决的难题[5].

当前主流的实时定位技术包括红外定位、射频识别（RFID）、蓝牙、无线局域网（Wi－Fi）、紫蜂（Zig－Bee）、全球定位系统（GPS）、超宽带（UWB）等.红外定位利用了红外线的测距功能，红外线在小范围封闭无干扰区域内的测距精度较高.Want等[6]设计了利用红外定位的活动徽章（Active Badge）系统，但是由于光的特性，其存在无法穿越墙壁等遮挡物的问题，且极易受到环境干扰，导致平均定位精度仅达5～10m，所以不适合应用于定位系统.RFID的定位原理类似于GPS定位，已知读写器的位置，通过测量标签上接收到读写器信号的强度估算标签坐标.RFID的代表性系统是Landmarc，系统采用“最近邻居”算法估计节点空间位置，定位精度为0.05～5m[7]，但该方法需要布置大量参考标签，实施复杂度高.蓝牙方法则利用信号强度信息，通过指纹法或信号传播模型法实现定位[8].蓝牙方法适用于小范围区域，如房间、小型仓库等地方.蓝牙设备体积小、功耗低，其缺点是信号传播范围较小、抗干扰性差，定位精度在2.5m 左右[9].Wi－Fi定位方法包括基于测距定位的方法和基于指纹定位的方法[10]，其布设成本低、难度小，原理与蓝牙定位类似，定位精度为2～5m.ZigBee方法常通过信号传播路径损耗模型估算节点之间的距离从而实现定位。其缺点是信号传输受多径效应和目标移动的影响较大，该方法的定位精度为1～8m[11－12].GPS则依赖于地球卫星，在室外空旷环境下可达到10m的定位精度，而室内则由于楼层遮挡导致接收信号衰减，所以不适合用于室内定位[12].

主流实时定位方案的研究中，定位精度范围为1～10m，抗干扰性差、误差波动大，用在戒毒所房间、走廊等小范围区域内极易发生定位错误，精度不能很好地满足强制戒毒人员的定位要求.近年来兴起的UWB通信技术具有抗干扰能力强、抗多径效应好、测距精度高等优点，非常适合于定位.为了实现对强制戒毒人员位置的精确管控，以UWB定位技术为研究对象，分析两种常见UWB测距算法的误差，进一步针对双向测距算法进行误差优化，引入一个天线延迟补偿参数，并提出一种延迟参数的简易调节方法.进行误差修正与参数调节后，系统的测距误差得到了控制，克服了传统ZigBee、Wi－Fi等方法在狭窄走廊和小型房间内定位不准的缺点.经过测试，测距误差与理论分析相符，系统的静态测距误差在7cm以内，测距频率在10Hz以上，定位精度在20cm以内，位置更新频率在5Hz以上.

所设计的定位系统由3部分构成：定位标签，内置于戒毒人员的可穿戴监护设备；定位基站作为参考，设置于固定位置；定位服务器，用于计算定位位置，显示人员所在位置并记录人员的活动轨迹.

1 测距算法与误差分析

测距系统的测量方法为飞行时间（TOF）法.TOF法最早由 Mccrady等[13]于2000年提出，后来经由 Gunther等[14]在电气与电子工程师协会（IEEE）802.11b无线局域网中用其作为测距技术，才逐渐应用于室内定位中.该测距公式为

式中：Tpro为信号传播时间；c为信号传播速度，取光速c＝299 792 458m／s（https：∥en.wikipedia.org／wiki／Speed＿of＿light）.TOF测距技术包括两种方法：单向测距（OWR）法和双向测距（TWR）法.OWR法需保证基站与标签之间的时钟完全同步，实现难度大，因此通常采用无需时钟同步的TWR法.TWR法又分为单边双向测距（SS－TWR）法和双边双向测距（DS－TWR）法两类.

1.1 SS－TWR法

SS－TWR法的消息机制如图1所示.标签A在时间t1发送测距请求，基站B接收到请求，记录下接收时间t2，经过Trep时间间隔，在t3时间向标签A返回应答数据，最后在时间t4，标签A接收到应答数据，测距完成.一次完整的测距过程共由“请求—应答”两条消息组成.标签A发出信息至接收到来自基站B的应答消息的时间间隔记为Tro，根据图1，Tpro可由式（2）求得后进而换算为距离

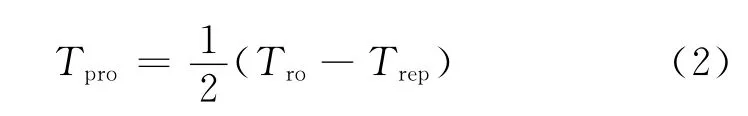
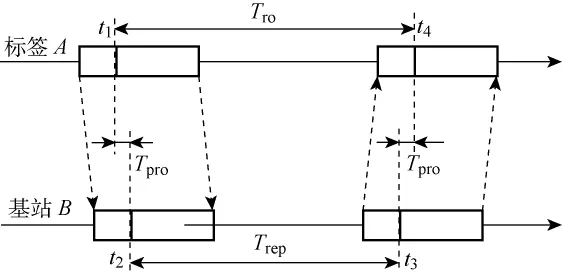
图1 SS－TWR法的消息机制Fig.1 Frame format of SS－TWR method

由于Tro和Trep分别由标签A和基站B各自的时钟计时器获得，其晶振难以保证工作频率准确工作于标称频率，因此会产生各自微小的频率偏差，频偏比例分别记为eA和eB.则信号传输时间Tpro的测量值与理论值Tpro之间的时间误差εt为

系统所采用的消息帧为16～24Byte，以110 kbit／s的速率发送，约需要1.16～1.74ms发送完毕.若标签与基站间隔50m，则Tpro约为167ns≪1.16ms，结合式（2），可近似认为Tro≈Trep.由式（3）可知，因eA与eB之间的差值固定，当Trep越大时，εt越大.因此，该方法在测量中应尽可能减小Trep以减小εt.将式（3）的时间误差换算为距离误差εd，其与Trep，eA－eB的关系如图2所示.

图2 εd 与Trep，eA－eB 的关系Fig.2 Relationship amongεdand Trep，eA－eB

1.2 DS－TWR法

DS－TWR法的消息机制如图3所示.与SSTWR法不同，DS－TWR法增加了一帧“结束”消息，即一次完整的测距过程由“请求—应答—结束”3条消息组成.通过精确采样t′1～t′66个发出或接收消息的时间点，计算T′ro1，T′rep1，T′ro2，T′rep24个时间间隔，利用式（4）求得信号的传输时间T′pro为

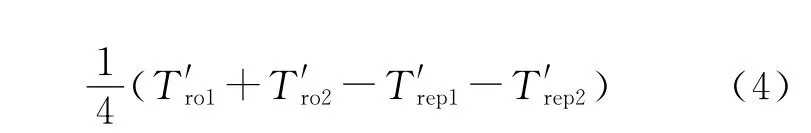
图3 DS－TWR法的消息机制Fig.3 Frame format of DS－TWR method

由于T′ro1，T′rep2由标签 A 的时钟采样计算，T′ro2，T′rep1由基站B的时钟采样计算，记标签A与基站B的时钟偏差分别为eA和eB.则信号传输时间T′pro的测量值和理论值T′pro的时间误差ε′t为

由式（5）可见，ε′t与T′rep1与T′rep2的差值成正比，且该差值越接近于0时，ε′t越小.该方法利用 “A→B”和“B→A”两次互补的测距过程，抵消了由于标签A与基站B之间的时钟偏差带来的误差.对比式（5）与式（3），因为ΔT′rep远小于Trep，所以 DS－TWR法比SS－TWR法的时间误差要小得多.

将式（5）的时间误差换算为距离误差ε′d，其与ΔT′rep，e′A－e′B之间的关系如图4所示.由于ε′d与ΔT′rep成正比，可以使ΔT′rep尽可能接近于0以减小误差，即“A→B”和“B→A”两次测距过程尽可能对称.

图4 ε′d与 ΔT′rep，e′A－e′B 的关系Fig.4 Relationship amongε′dandΔT′rep，e′A－e′B

1.3 DS－TWR非对称测距误差修正

实际中，Trep1依赖于标签A的时钟，而Trep2依赖于基站B的时钟，两者的计时器相互独立，使ΔT″rep等于0是非常困难的.因此，在DS－TWR法的基础上，对误差进行了进一步修正，称为非对称双边测距（ADS－TWR）.修正后，计算信号传播时间T″pro的公式为

简述式（7）的建立过程.假设时钟标准工作频率为1Hz，标签A的时钟频率为标准时钟的kA倍，基站B的时钟频率为标准时钟的kB倍，且有

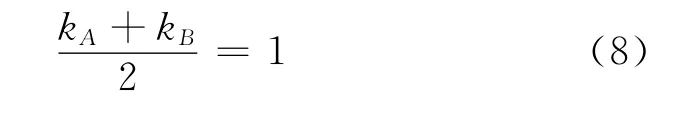
则根据图3有如下关系式：

将式（8）代入式（9）可得

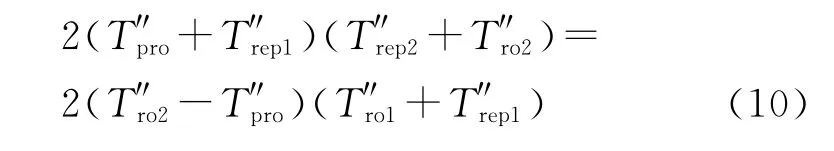
进一步化简，即可得到式（7）.

该方法基于假设标签A与基站B时钟频率的平均值等于标准时钟频率，因此时间误差ε″t只与两者时钟频率平均值与标准时钟的偏差有关，尤其对于标签A与基站B的时钟频偏为一正一负的系统精度更高.ε″t的表达为

由式（11）可知，ε″t不与 ΔT″rep相关，克服了 DSTWR法中误差与ΔT′rep线性相关的问题，进一步减小了非对称情况下的距离误差ε″d，尤其对于标签A与基站B的时钟频偏为一正一负的情况，精度更高.ε″d与距离S、时钟偏差σ的关系如图5所示，其中，ε″d由式（11）中的ε″t换算而来.

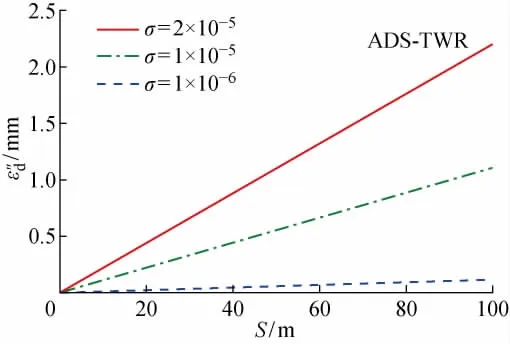
图5 ε″d与S，σ之间的关系Fig.5 Relationship amongε″dand S，σ

2 测距系统设计

2.1 测距模块设计

测距系统选用Decawave公司生产的DW1000超宽 带 通 信 芯 片，符 合 IEEE802.15.4－2011[15]标准，支持高达6.8Mb／s的通信速率，具有强抗多径能力，低功耗和高可靠性等优点，非常适合用于高精度测距.测距系统由 ARM（Advanced RISC Machines）微控制器（MCU）、DWM1000收发模块、有机发光二极管（OLED）显示屏幕、串口和上位机构成，如图6（a）所示.系统基站实物图如图6（b）所示，其尺寸约为51mm×35mm，标签与基站采用同样的硬件设计结构.ARM微控制器与DWM1000收发模块之间通过串行外围设备接口（SPI）协议连接，与OLED屏幕之间通过集成电路总线（IIC）连接，与上位机之间通过串口通用异步收发传输器（UART）连接.OLED屏幕用于显示测距结果与显示系统状态，上位机用于调节系统延迟等参数，显示、存储测距结果以方便管理.

图6 测距系统的结构图与实物图Fig.6 The structure chart and photo of ranging system

选择性能最佳的ADS－TWR法作为测距算法，由于算法误差不受ΔT″rep影响，系统可在单一基站与多标签同时测距的情况下保持相同精度.此外，在数据信号开始传输后需经过微波放大电路和天线等模块，会给传输过程带来一定的延迟，因此消息实际发出或接收的时间与采样时间有所偏差.由于信号传播速度极快，信号延迟不可忽略不计.

针对这一问题，引入一个延迟参量τ，用于补偿电路与天线所带来的延迟.此参数的标准校准过程需要在生产线上经过高精度时间采样设备和控制设备完成.普通应用难以实现这种标准的校准条件，而且延迟参数因电路设计的不同各不相同，因此本文提出一种简易而有效的、基于Monte Carlo法[16]的延迟校准方法.

2.2 系统延迟参数校准

τ用于补偿微波放大器和天线引入的延迟，校准的思路为：使发送端与接收端相隔固定距离放置，借助Monte Carlo法，随机生成若干组参数以评估各组参数设置下的系统效果，进而筛选出最佳参数τ，即获得延迟参数.该方法简单易行且有效，校准算法执行过程如下.

（1）准备工作.将标签A与基站B相隔固定的距离la对向放置，两者天线要正向相对，基站B通过串口连接至校准计算机.

（2）设置初始值.在校准软件中设置迭代次数N；参数的初始值；微调步长Δτ，τ的取值范围为0～65 535，对应的延迟时间范围为0～1 025ns[17].校准软件随机生成n组延迟参数Di＝ （τA，τB），分别代表标签A的延迟参数及基站B的延迟参数.执行N次迭代过程.

（3）进行一次迭代过程.在上一步骤生成的n组延迟参数中，校准软件依次把每组延迟参数通过串口发送至基站B，基站B存储τB，同时将τA通过消息发送至标签A.随后基站B以及标签A分别进行500次DS－TWR法测距过程，结果经由基站B的串口回传至校准软件，校准软件取均值获得本次测量距离结果Li＝ （lABi，lBAi）.其中，lABi为标签A向基站B测距的结果；lBAi为基站B向标签A测距的结果.重复步骤3直到完成n组延迟参数的设置与测距.

（4）对n组延迟参数结果进行评估筛选.定义误差评价函数Fi＝Li－La2，其中La＝ （la，la）为A与B之间的已知距离.该步骤分为3步：

① 计算n组延迟参数各自的评价函数Fi，筛选出函数值最小的25%延迟参数加入新一次迭代中的n组延迟参数中.

② 将筛选出的25%延迟参数分别叠加±Δτ变化量，加入新一次迭代的n组延迟参数.

③最后，利用随机生成法生成剩余的50%延迟参数.重复步骤③，进行下一次迭代.

（5）达到迭代次数N，校准结束.以最终结果中评价函数值最小的延迟参数作为最终的延迟参数校准值Dca＝ （τA，τB），至此校准完成.

参数校准调节的流程框图如图7所示，其中，虚线框为“计算误差函数，更新延迟参数”的子程序框图.

图7 校准算法框图Fig.7 Flowchart of calibration algorithm

3 定位系统设计

定位系统以测距系统为基础扩展而来，由3个基站，1个标签构成.基站1通过串口连接到上位机，将测距信息回传至定位软件，由定位软件计算、估计出标签的最佳实时位置，并进行显示绘图.

三边－质心测量定位法[12]被用于计算标签的位置，在固定位置放置3个不共线的基站B1，B2，B3，标签A分别与3个基站进行测距，测得距离为r1，r2，r3.分别以3个基站为圆心，3个距离为半径画圆，3个圆的交点位置即为标签A的位置.

设标签A的坐标位置为（x，y），基站B1，B2，B3的坐标位置分别为（x1，y1），（x2，y2），（x3，y3），利用 ADS－TWR法测得的距离分别为r1，r2，r3，则有如下关系：

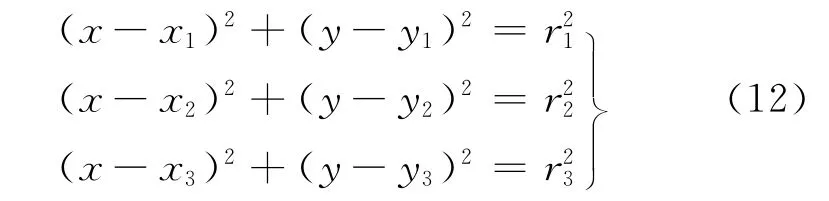
式（12）有3个方程，2个未知数，为超静定方程，故使用非线性最小二乘法求解，利用Taylor级数展开法近似计算使得误差最小，进而估计出标签的最佳位置.

三边定位算法的误差取决于两个因素：基站的几何分布和各测量值的大小[18].文献[19]中的仿真结果表明：当基站数量较多时，将其按照蜂窝型布置获得的定位误差最小.在三基站的系统中，将其摆放于等边三角形的3个顶点即可.

4 系统测试与结果分析

对系统进行4项基本测试：延迟参数校准、静态测距、静态与动态定位和功耗测试.场地为开阔无障碍物的大厅，各基站架设于三脚架上，距离地面高为75cm.系统的通信速率为110kbit／s，发送数据帧有“请求”，“应答”和“结束”3种.除IEEE802.15.4－2011[16]标准中规定的前导码外，还包括数据（Data）部分，其发射长度分别为12，16，24Byte.数据部分包含帧识别字，帧序号，发送设备地址，接收设备地址，时间戳，测量结果，校验字等多种信息.

4.1 延迟参数校准测试

所提算法的搜索校准过程如图8所示.其中，τA为标签A的延迟参数；τB为基站B的延迟参数；j为迭代次数；红色“×”点为每次迭代中搜索到的最优参数；蓝色点为随机生成的其他参数.由图8可知，每次迭代均能缩小最优参数所在范围，在第12次迭代时，最优延迟参数已经收敛至某一点附近，在达到最大迭代次数时，将获得最优参数.最终，所设计模块的延迟参数校准在32 900附近，换算为实际时间约为515ns.将参数写入DW1000芯片保存.

图8 最优延迟参数搜索过程Fig.8 Process of searching best delay parameters

4.2 双向测距静态测试

使用单基站与单标签进行双向测距测试，分别使用SS－TWR法，DS－TWR法和经过改进的ADSTWR3种测距方法进行静态测距实验.在100～2 000cm范围内每隔200cm等间隔选择10个测距位置点，每个点执行200次测距.3种方法在测量前均已进行模块延迟的校准修正.

3种测距方法的测距误差ε3d与均方误差（MSE）如图9所示.由图9可知，SS－TWR法的测距误差最大，距离较近时测距精度较差.随着距离的不断增加，误差有所降低，但依旧有15cm以上的测距误差，且随着距离持续增大，误差也在持续增加.DS－TWR法的测距误差较小，无论距离远近，其测距误差始终在10cm以内.改进的ADS－TWR法的测距误差与DS－TWR法持平，测距误差保持在10 cm以下的同时，在各测距点的误差水平都比较稳定，而且在测距距离达到20m时依旧具有5cm的高精度.3种测距方法的误差水平与前文的理论分析相符.

图9 3种测距方法的测距误差和均方误差Fig.9 Ranging error and mean square errors of three algorithms

考虑到功耗问题，实验设定为测距完成休眠一段时间后再执行下一次测距，频率控制在10Hz，通过软件计时测得的一次测距周期为0.096s.

4.3 测距系统功耗分析

通过测量系统工作时的电流电压分析其功耗水平.测量仪器选用正泰ZTY1201A电流电压检测仪.在不间断地持续工作时，测距频率约为62Hz，标签电压为5.08V，电流为0.11A，算得的功率为0.559W.考虑到标签需内置于可穿戴设备，如持续工作功耗过大，将严重影响电池寿命，故权衡测距频率和功耗，保证测量精度与分辨率的同时，降低测量频率.相邻两次测量之间，设备处于休眠模式以节省功耗.设置测距频率保持在10Hz，此时测得电压为5.10V，电流为0.05A，功率为0.255W.使用3.7 V，1 350mA·h的锂聚合物电池供电，续航时间为14～16h，可满足一天内的使用需求.

测距频率选择10Hz，定位频率选择5Hz，当目标移动速度为1.2m／s时，分别具有12cm和24cm的分辨率，实现功耗与分辨率的平衡，能够满足戒毒所场景中的测距定位需求.

4.4 定位系统测试

基于三边－质心定位法，设计实验测试系统的定位精度，定位系统所采用的测距方法为基于改进误差的ADS－TWR法.将3个基站B1～B3放置于边长为8m的等边三角形的3个顶点处，坐标为（0，0）m，（8，0）m，（4，4）m，其构成的测试区域为一个边长为8m，宽为4m的长方形，约为一房间的面积.

4.4.1 单目标系统定位测试 单目标定位系统测试如图10所示，其中，绿色正方形为基站；红色点为预先选取的测试点；红色虚线为移动路线；蓝色点为实测位置点.测试分为两部分：① 在基站围成的区域内，设测试点为Pi，Qi，i＝1～4.测试目标沿随身携带的标签沿红色虚线以 “P1—P4，P4—Q4，Q4—Q1”路径平稳缓慢移动，并在每个点处停留1 min，进行区域内的定位测试.② 测试目标沿随身携带的标签沿红色虚线以“B1—B2—B3”路径平稳缓慢移动，并在每个点处停留1min，进行边界点的定位测试.

图10 单目标定位系统测试图Fig.10 Single object location system tests

由图10可知，目标在缓慢移动的测试中，很好地贴合了设定的红色虚线轨迹.总计11个测试点的平均误差和MSE1如图11所示.结合图10可知，系统具有稳定且良好的静态测量精度，无论是在区域内还是在边界点即与基站重合的位置，测试点的方差都较小.由图11可知，静态情况下的最大值在18cm，最小值可达到5cm以内，所有测试点的为12.25cm，误差范围为4～20cm，静态情况下测试点的方差均较小.对位置测量时间进行计时，平均每次定位耗时0.186s，位置刷新频率达到5Hz以上，能够保持对行走目标定位的高分辨率.

4.4.2 多目标系统定位测试 实际应用中，往往需要对多个目标、不同速度运动的动态目标进行定位.在单目标测试中，标签依次向3个基站测距，即可完成定位.当目标增加后，多个目标同时向基站发起测距请求，数据量增大，难免出现数据帧拥挤碰撞的问题.受到Cricket系统[20]中处理冲突方法的启发，采用动态随机设置测距休眠间隔的方法，减少数据帧碰撞的概率以降低标签之间的相互干扰.

多目标定位系统测试如图12所示，其中，tag0和tag1分别代表两个运动目标，tag1分别在Q1，Q2，Q3（纵坐标为2m，横坐标依次为1m，3m，5m）3个点进行测试，同时，tag0对应处在P1，P2，P33个点（纵坐标为4m，横坐标同tag1）；.由图12可知，当对多目标同时进行测试时，定位的平均误差为12.59cm，误差范围在8～20cm，精度与单目标定位接近；而定位的MSE2相比单目标定位有所增大，其原因是多目标同时定位会产生消息碰撞的问题，部分测距信息帧丢失，同时标签之间还存在相互干扰，最终导致测距结果的方差变大，在不增加功耗提升测距频率的情况下，基于测距的定位刷新频率也降至3～5Hz，难以稳定在5Hz.

图11 单目标定位测试的ε－与MSE1曲线Fig.11 Theε－and MSE1of single object location test

图12 多目标定位测试Fig.12 Multi－object location test

5 结语

为实现对人员的安全、身心、健康等方面的全方位监控，本文设计了一种用于戒毒所人员实时位置定位和管理的系统，弥补早期定位方案中的不足之处，提出延迟参数的简易调节方法，进一步对测距中的误差进行优化减小，达到了厘米级的测距和定位精度.所设计的UWB测距定位系统包含测距与定位两个功能，支持室内与户外铺设的使用.高精度测距功能实现了高达7cm的测距精度，10Hz的距离刷新频率，可在外勤时限制强制戒毒人员的活动范围，及时发现逃离事件；定位功能达到了20cm的定位精度，5Hz的刷新频率，可对区域内的人员位置进行精确定位与显示，便于戒毒所内人员位置的可视化管理.测距定位系统将与戒毒所内的管理系统深度结合，形成更加完善的安全监护体系.