移动GPU上基于轻量级卷积神经网络的道路拥堵检测方法
2020-01-14全美娟陈庆奎
全美娟,陈庆奎
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
随着城市的发展,城市道路拥堵问题已然变得十分严峻,一个强大的智能交通监控系统对于每一个现代化城市而言都是非常必要的.其中,道路拥堵检测技术在智能交通系统领域具有极其重要的地位.传统的道路拥堵检测技术会有破坏路面,安装与维护难,成本高等缺点.相反,通过交通监控视频处理技术[1-3]来进行车辆密度检测具有很大的优势.近年来随着深度学习在图像处理等领域扮演着越来越重要的角色,已有研究人员想要在移动设备上进行深度学习框架的移植[4].但是,由于卷积神经网络模型庞大的计算量,导致移植程序在性能受限的移动设备上难以取得较好的检测效果.
伴随深度学习技术的发展,当前卷积神经网络技术的发展是趋向更深更复杂的结构体系,以此来获得更高的精度.虽然深层卷积网络在NVIDIA GTX 1080等高配置GPU上能够达到实时性的要求,但是在一些计算性能有限的移动平台上,很难达到实时要求.如何在计算性能受限的设备,尤其是小型嵌入式设备上进行检测仍是当前研究的热门方向.本文研究的主要方向是在功耗和计算性能受限的移动 GPU 平台上实现基于车辆密度的道路拥堵检测,对于智能交通系统领域而言具有创新性和挑战性.
本文基于Caffe框架,在移动GPU上利用改进的轻量化SqueezeNet网络对城市道路路口视频图像进行基于车辆密度的分类,并结合本文提出的道路拥堵判断方法来实时判断各车道的拥堵状态.实验结果表明,改进的SqueezeNet网络可在保证较高准确率的同时减少参数量,与拥堵状态判断模型的结合能够高效的实现道路拥堵检测任务.
2 相关工作
深度学习的概念由Hinton等人于2006年提出,并在计算机视觉、语音识别和自然语言处理中的许多问题上有杰出的表现.但是,深度学习模型的共同点是计算复杂度高,参数规模大,不能够在性能受限的移动设备上大规模应用.因此,轻量化的网络模型以及模型压缩技术愈发受到开发者的青睐.轻量化的网络模型是通过设计浅层网络来实现对深度学习模型识别效果的逼近,本质上也是一种有效的模型压缩思路.这些网络模型的参数较少,层数不多,具有代表性的网络有MobileNet、ShuffleNet、SqueezeNet.2016年,FN.Iandola[5]等人提出的SqueezeNet网络模型通过将大量的3*3卷积核转换为1*1卷积核以及减少3*3卷积核的通道数,同时将一个卷积层分解为一个squeeze层和一个expend层,在大规模缩减参数规模的同时保持和AlexNet相当的准确度.2017年Google提出了一个针对移动设备、嵌入式设备等的轻量化网络模型MobileNet[6].MobileNet采用了大量的通道分组卷积层(Depthwise Separable Convolution)结构,分组卷积模块的参数量比标准卷积缩小了约8-9倍,但对准确率的影响甚小.
传统针对道路拥堵检测[7]来获取诸多交通特征参数的方法有环形线圈法、雷达(微波)法、超声波法等.但这些方法存在着很多缺点,如环形线圈法安装不方便,影响路面寿命,有较大的识别误差.雷达(微波)法和超声波法不能检测静止或低速行驶的车辆,检测性能随温度和气流影响而降低.而由于视频监控安装简单,成本较低,导致开发商对视频处理的关注度持续上升.针对传统道路拥堵检测方法的弊端,结合基于深度学习视频处理技术的优势,本文提出了基于视频处理技术的道路拥堵判断方案.该方案能够在提供较高判断准确率的前提下,减小安装维护的成本,灵活性以及简便性较强,为大量的推广和普及提供了基础.
3 道路拥堵检测方法
针对在移动GPU上实现基于车辆密度的道路拥堵检测问题,由于移动GPU的存储容量较小以及计算性能有限等特点,我们对轻量化SqueezeNet1.1网络进行改进,并实现在移动GPU上进行图像分类模型的训练.结合该分类模型检测出的各车道在各时刻的车辆密度分类状态序列和本文提出的道路拥堵判断模型来实时判断各车道的拥堵状态.
3.1 检测方法框架
本文利用改进的轻量化SqueezeNet网络进行基于车辆密度的图像分类模型训练,并用该分类模型对视频进行检测.为减小移动GPU的计算压力,我们采用间隔采样(如间隔1秒)的方法提取视频帧进行检测,并记录各车道在各时刻的车辆密度分类状态序列.结合分类状态时间序列分析判断各车道当前时刻是否拥堵.整体检测方法流程图见图1.
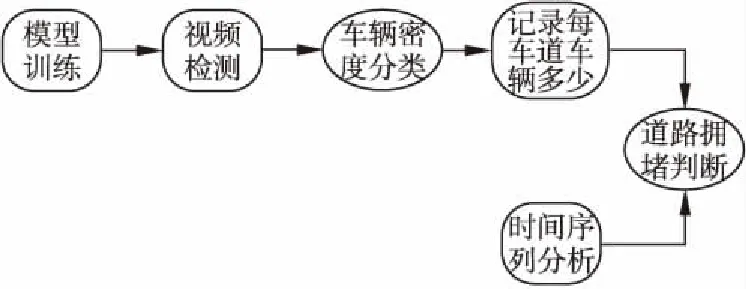
图1 检测方法流程图Fig.1 Flow chart of detection method
3.2 模型训练
虽然使用更深、更复杂的卷积神经网络结构能够获得更高的检测精度,但是其庞大的参数量以及计算量使其对部署设备的GPU性能有着严格的要求.针对移动GPU环境而言,网络模型的轻量化工作无疑是必须.轻量化的网络模型需要考虑模型的存储问题和模型预测的效率问题.在众多网络模型中,轻量化的SqueezeNet能够在大规模缩减参数规模的同时保持和AlexNet相当的准确度.因此,本文在SqueezeNet1.1网络的基础上进行参数的优化、网络结构的调整,使网络模型参数量减少的同时保证了分类检测的准确度,得到较好的性能.
3.2.1 模型结构
改进的轻量化SqueezeNet网络的网络结构见图2.该网络可在不损失分类检测准确度的同时将模型大小压缩至AlexNet网络模型大小的0.023倍,其模型大小只有2.78MB左右.本文的改进策略有如下2点:
1)相比SqueezeNet1.1而言,减少部分上层的num_output数,即减小输入到下层的通道数
2)为保留更多的信息,在SqueezeNet1.1基础上,我们调整网络结构,置后池化层位置,从而获得更高的精度
3.2.2 Fire Module模块
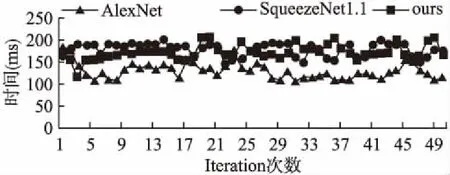
SqueezeNet的核心模块为Fire Module模块[8]见图3,类似于Inception网络结构单元.Fire Module模块由两层构成,分别为squeeze层和expand层,同时各自还连接了一个ReLU激活层.squeeze层只包含1*1的卷积核,其数量为s1,expand层包含1*1的卷积核和3*3的卷积核,其中1*1卷积核的数量为e1,3*3卷积核的数量为e3,并且s1 3.2.3 池化操作 由于参数量以及计算量巨大,通常在网络结构的卷积层之间加上pooling池化层.这不仅可以减少参数、防止过拟合、提高模型性能,还可以提升整体的检测精度.为最大化的保持原图特征,通过调整网络结构,改变池化层的位置来改进SqueezeNet网络结构,从而获得更高的精度.本文采用max-pooling的池化操作来对数据进行降采样.当卷积层的输出大小为4*4,池化层过滤器filter大小为2*2,步长stride为2,那么经过池化层处理后,输出数据的大小为2*2,骤减到池化操作前的1/4.经池化操作后输出的特征图大小计算公式如公式(1): (1) 图2 SqueezeNet网络结构对比图Fig.2 SqueezeNet network structure contrast diagram 3.2.4 车辆密度分类 本文在基于车辆密度的基础上利用卷积神经网络实现图像分类[9-11].图像分类检测的主要流程见图4,主要任务是对路口各车道在各时刻车辆密度进行分类检测. 对于上海市某段包括右转车道、直行车道、左转车道的路口,我们根据各车道车辆密度的多少制定出8类标签,见图5.若当前车道的密度大,车辆铺满整个车道,则标记为多;若当前车道的密度低,车辆没有铺满整个车道,道路后方路面未被遮挡区域较多,则标记为少. 3.2.5 道路拥堵判断模型 已有研究人员利用视频前后帧图像相似度的方法来判断道路是否拥堵.对于光照变化、车辆款式相同以及车辆等待绿灯等情况造成的影响,利用图像相似度来检测道路是否拥堵的方法会造成很大的误差.此外,根据车道车辆状态序列的状态持续时长来判断这段时间内车道是否拥堵的方法存在很多弊端.例如,若这段时间内某些时刻的状态检测有误,则状态序列片段中会出现噪声,从而影响拥堵判断的准确率.记车道的状态序列为S={s1,s2,s3,s4,…,sk}(k为视频中的时刻),S可以分割为一个个序列片段,则车道的状态序列可表示为S={N1,N2,N3,N4,…,Nf}(f为序列片段数).其中某一状态序列片段集Ni={sm,sm+1,…,sn}的状态均为多,且持续时间大于阈值,则认为该车道在这段时间内是拥堵的.如果这个片段Ni中出现噪声,干扰了状态序列片段Ni,那么该车道在这段时间内会被误判为不堵. 图3 Fire module模块单元Fig.3 Fire module unit 据此,本文结合分类状态时间序列提出了一种新颖的道路车道拥堵判断方法.通过在红绿灯信号周期的基础上进行时间序列的分析可将车辆的运动和静止状态有效的区分开.连续的“红—绿”时间段称为一个信号周期T(本文忽略黄灯,将黄灯显示时间并入绿灯时间),而各个路口的红绿灯信号周期T虽各不相同,但已知.一个信号周期T可以分别对不同方向的交通流分配不同的相位,对于实验中的上海市某段路口,红绿灯信号周期T由三个相位组成,相互独立,各个相位周期性交替获得绿灯显示,见图6. 图6 相位图Fig.6 Phase map 路口的右转车道、直行车道以及左转车道的灯色显示都遵循红绿灯信号周期T,循环显示“红—绿”状态.对于各车道来说,我们已经利用图像分类模型检测出各时刻各车道车辆密度的分类状态,得到基于车辆密度分类的状态序列,然后在基于红绿灯信号周期的拥堵状态判断模型上,结合历史分类状态时间序列和当前分类状态来判断当前时刻各车道是否拥堵. 根据本文的判断方法,若当前t时刻,直行车道的车辆处于静止状态,1个信号周期前的t-T时刻和2个信号周期前的t-2T时刻的车辆必然处于静止状态,反之,当t时刻车辆处于运动状态,1个信号周期前的t-T时刻和2个信号周期前的t-2T时刻的车辆也必然处于运动状态.此方法可以有效的将各时刻道路上车辆运动和静止状态区分开,如图7所示.依据{…,t-2T,t-T,t}连续n个周期时刻直行车道车辆的状态{…,st-2T,st-T,st}均为多,即经过连续n个周期时间,车辆多的状态仍没得到缓解,则说明存在很多车辆的堆积.显然当前t时刻的直行车道是拥堵的,因此我们可判断出当前t时刻的直行车道是拥堵的. 图7 各车道基于信号周期的时间序列Fig.7 Time series of lanes based on signal period 我们将本文提出的拥堵判断方法封装为拥堵状态判断模型,建立如下的数学模型: A(T,t,n)={Pn(t-nT),…,P2(t-2T),P1(t-T)} (2) E=G(P,A,t,T,n)n∈{1,2,…} (3) 其中t表示当前时刻,T表示信号周期的时间,n为正整数表示信号周期的数目,图8为n=2时的拥堵状态判断模型,A表示早期的时间状态序列集,P(t)=[SL,SM,SR]表示t时刻各车道的状态序列数组,L、M以及R分别表示左转车道、直行车道以及右转车道,G为本文的拥堵状态判断模型,E(t)=[OL,OM,OR]表示t时刻各车道拥堵与否的状态序列数组. 图8 拥堵状态判断模型Fig.8 Congestion state judgment model 本文所提出的拥堵判断方法能够判断出当前时刻各车道是否拥堵,将车辆的运动状态和静止状态有效的区分开.通过控制n的取值,在一定程度上可以预测当前时刻的车道上是否有异常事件的发生,如上下班的高峰,车祸事件等. 我们给出本文单车道拥堵判断算法的部分伪代码: Algorithmofcongestiondetectioninsinglelane IF Signal period is not null THEN Read T from Signal period ELSE T=120 END IF Get the current time t from the video Input State Sequence ArraySM=[{si}] IFt CONTINUE ELSE IFst=st-T=st-2T=…=st-nT="numerous" THEN the current time lane is congested ELSE the current time lane is not congested END IF Output the Congestion Sequence Array 本文实验的硬件环境如下:移动处理器Tegra K1搭载NVIDIA 4-加-1(4-Plus-1TM)四核ARM®CortexTM-A15的CPU,以及包含192个NVIDIA CUDA®核心的NVIDIA KeplerTMGPU,8GB的内存容量,2.3GHz的时钟频率.开发环境如下:配置OpenCV图像处理库,CUDA-6.5并行计算库,并搭载对应版本的cudnn-6.5-linux-ARMv7-v2并行加速库以及cudnnv2版本对应的Caffe框架.实验所采用的数据集均采集于上海市某路口不同时间段的交通视频. 根据采集的道路交通视频,利用工具提取视频帧图片作为数据集.其中153858张图片作为训练数据集,85650张图片作为测试集.该路口有右转车道、直行车道、左转车道,根据分类规则对每张图片进行分类标记. 在Caffe框架下,利用训练数据集对改进的SqueezeNet网络模型进行训练.训练过程中,使用poly的学习策略,初始学习率base_lr设置为0.002,最大迭代次数max_iter设置为29000次,学习率依照learning_rate(1-iter/max_iter) ^(power)不断进行变化,为了防止过拟合,权重衰减系数weight_decay设置为0.0005. 传统AlexNet网络模型的网络结构比较简单,卷积层数为5.SqueezeNet的网络结构稍微复杂一点,卷积层数为26层,是AlexNet的5倍以上.通过在低端的移动GPU TegraK1上测试模型50次迭代的总运行时间(见图9),AlexNet网络的测试结果为6531.77 ms,SqueezeNet1.1网络的测试结果为8933.26 ms,本文改进的SqueezeNet网络的测试结果为8612.26 ms.通过比较,在卷积层数增加了5倍左右的情况下,本文改进的SqueezeNet网络50次迭代的总运行时间较AlexNet网络的总运行时间只增加了32%左右.对比SqueezeNet1.1网络50次迭代的总运行时间,本文改进的SqueezeNet网络50次迭代的总运行时间缩短了3.59%. 图9 模型运行时间对比图Fig.9 Model runtime contrast diagram 4.3.1 模型大小 由于移动GPU的计算性能有限,存储容量较小,在此平台上部署网络模型需要控制模型规模.而本文改进的SqueezeNet模型大小为2850KB,与传统AlexNet模型相比缩小了43倍(见表1),满足在移动GPU上的部署需求. 表1 改进的SqueezeNet模型与传统AlexNet模型对比 网络结构模型大小与Alext对比模型大小的减少AlexNet123950KB1xSqueezeNet2850KB43x 4.3.2 参数量 通过统计,传统AlexNet网络模型所包含的参数量(如表2)达到了3745824,SqueezeNet1.1网络模型的参数量为723136.文改进的SqueezeNet网络模型的参数量缩减到了544416,与传统AlexNet网络模型相比缩小了6.9倍,比SqueezeNet1.1网络模型减少了1/4,实现了网络模型的轻量化,为在移动GPU上的部署奠定了基础. 表2 模型参数量 模型输入大小输出大小总参数量AlexNet119*159*37*9*2563745824SqueezeNet1.1119*159*37*9*7723136ours119*159*37*9*7544416 4.4.1 模型准确率分析 为了验证本文改进后网络模型的检测准确度以及改进效果,使用测试集对训练出的模型与SqueezeNet1.1网络模型进行8类道路路况的准确度验证,测试结果如图10所示. 图10 SqueezeNet1.1与改进的SqueezeNet模型测试正确率对比Fig.10 Comparison of squeezeNet 1.1 and improved squeezeNet model test accuracy 实验结果表明,改进的网络模型在减少了参数量的同时,其检测准确率并未下降.对8类道路路况检测简易程度的各不相同,导致实验中各类别道路路况检测准确率不同.例如上图中类别1,对应各车道为少少少的路况,针对这种稀疏的对象检测,卷积神经网络能够提供极高的准确率,因此本文模型对其检测的准确率达到98%以上是合理的.但是数据样本的不均衡也会对8类道路路况检测准确率产生一定程度的影响. 4.4.2 道路拥堵判断准确率分析 根据采集的上海市某路口的交通视频,分别对时间段为06:00-09:00、11:00-14:00、16:00-19:00、21:00-24:00的视频进行逐秒标注拥堵状态. 为了验证本文提出的道路拥堵判断模型对各车道拥堵判断的准确率,我们提出了拥堵状态判断的评价指标.首先统计多段视频中(本文间隔1秒采样视频帧图片)各车道的拥堵状态序列,记为Eorigin=[EL,EM,ER].然后利用本文的拥堵状态判断模型判断得到各车道的拥堵状态序列,记为Etest=[EL,EM,ER].再对状态序列Eorigin和状态序列Etest进行逐一匹配,若状态相同则检测正确,反之检测错误,得到匹配序列V=[VL,VM,VR].最后统计匹配序列V中各车道检测正确的长度,记为length(V1),则各车道拥堵判断准确率的评价指标为: (4) 本文针对在拥堵状态判断模型中正整数n取值的不同,分别对各车道在不同时间段的2段视频进行实验,得到信号周期数目n对各车道道路拥堵检测结果的影响. 表3 不同n值下右转车道的拥堵检测准确率 实验序号视频数时间段n=1n=2n=3n=41206:00-09:0081.6%95.7%88.7%74.2%2211:00-14:0084.7%89.2%79.6%72.4%3216:00-19:0089.8%88.6%89.3%77.3%4221:00-24:0086.5%93.7%88.3%80.7% 表3的几组实验为不同信号周期数目的情况下右转车道在06:00-09:00、11:00-14:00、16:00-19:00、21:00-24:00时间段里的拥堵检测准确率.实验1、2以及4的情况下,n取值为2时,实验3中n为1时准确率最高比n为2时的准确率仅高1.2%.表4及表5分别为各时间段里不同n值下直行车道以及左转车道的道路拥堵检测准确率,当信号周期数目n取2时,拥堵的检测准确率最高. 表4 不同n值下直行车道的拥堵检测准确率 实验序号视频数时间段n=1n=2n=3n=41206:00-09:0087.3%90.7%84.6%79.2%2211:00-14:0085.7%88.6%87.6%72.4%3216:00-19:0079.8%89.2%77.2%76.3%4221:00-24:0084.4%88.5%80.8%78.3% 从不同n取值情况下各车道拥堵检测准确率的整体结果观测来看,当信号周期数目n取2时,道路拥堵的检测准确率最高,因此后续实验中n的取值设为2. 在信号周期数目n取值为2的情况下,分别对06:00-09:00、11:00-14:00、16:00-19:00以及21:00-24:00时间段的5个视频进行准确率的检测实验,最终检测结果取其平均值,各车道拥堵检测准确率的结果见表6.纵观实验数据,本文的道路拥堵判断模型对各车道道路拥堵判断的准确率均高于85%. 表5 不同n值下左转车道的拥堵检测准确率 实验序号视频数时间段n=1n=2n=3n=41206:00-09:0086.8%93.5%84.6%79.2%2211:00-14:0089.1%91.6%89.7%71.5%3216:00-19:0083.2%87.7%87.2%77.3%4221:00-24:0085.7%89.3%88.6%80.8% 表6 各车道的拥堵检测准确率 实验序号视频数时间段右转车道直行车道左转车道1506:00-09:0095.2%89.7%94.3%2511:00-14:0088.7%89.6%92.4%3516:00-19:0089.8%87.2%86.3%4521:00-24:0094.4%88.3%86.8% 针对移动GPU的道路拥堵检测问题,本文利用改进的深度学习网络SqueezeNet实现了基于车辆密度的分类检测模型.通过与传统的深度学习网络模型进行对比,验证了本文对SqueezeNet改进的有效性,在保持较高准确率的情况下实现网络模型轻量化.结合基于红绿灯信号周期的拥堵状态判断模型可减少因车辆等待绿灯而被误判的影响,高效率的实现了在移动GPU上判断各车道实时拥堵状态的任务,这对智能交通系统领域而言具有重要意义.本文下一步研究的重点是结合新型的MobileNet等网络模型,进一步提高基于车辆密度的分类检测模型的准确率以及降低模型的规模和占用空间,使其适用于性能更低的移动平台.


4 实验及分析
4.1 训练过程
4.2 模型运行时间
4.3 模型大小及参数量
Table 1 Comparing the improved SqueezeNet model with the traditional AlexNet model
Table 2 Model parameters
4.4 准确率分析
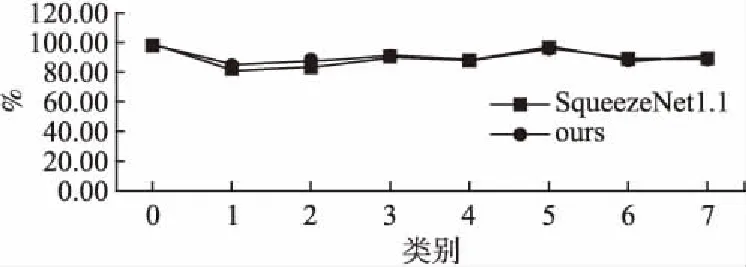
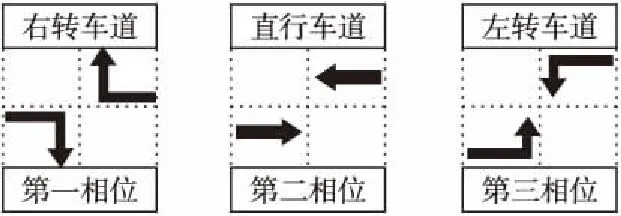
Table 3 Accuracy of congestion detection in right-turn lanes with differentnvalues
Table 4 Accuracy of congestion detection in straight lanes with differentnvalues
Table 5 Accuracy of congestion detection in left-turn lanes with differentnvalues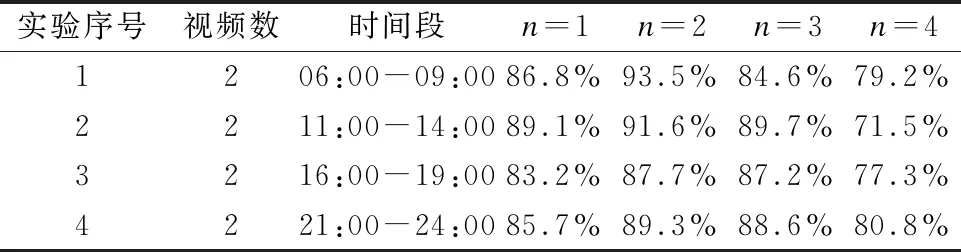
Table 6 Accuracy of congestion detection in each lane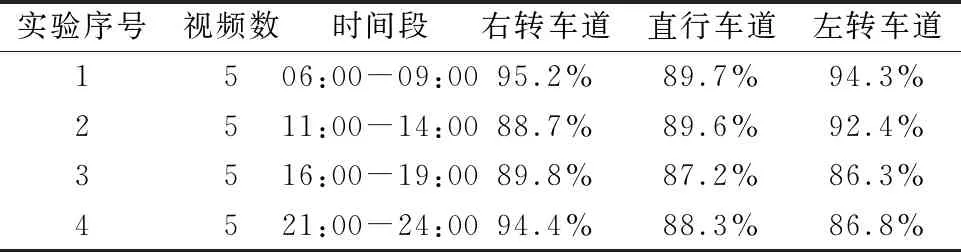
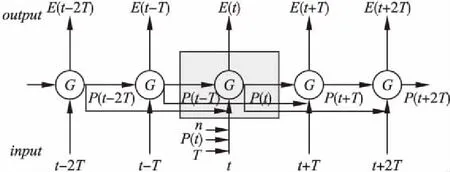
5 结 语
