竖向荷载下转体桥球铰接触面应力有限元分析

魏素文

(中铁十八局集团北京工程有限公司，北京 100162)

为确保新建桥梁跨越既有铁路及公路的施工安全，减少对既有铁路、公路运营的干扰，转体施工法成为跨线连续梁桥施工的主要方法[1]。在转体桥的转体系统中，球铰是最为重要的受力构件，其受力状态关系到球铰的设计尺寸及转体过程的顺利安全[2]。球铰受力是平转法施工桥梁在结构分析、设计优化、施工控制等方面的关键控制要素[3]。

当前转体系统球铰应力的计算理论主要依据规范算法，假设球铰上、下转盘之间的接触面为平面，不考虑球面影响，假设上部结构产生均匀压应力，以此得到简化后的计算结果，并根据该结果作为控制依据进行转动系统及牵引系统构造设计[4]，规范算法受力简单，计算方便，但是存在一定误差[5]。

本文利用Abaqus2019软件建立了转体桥转体系统有限元模型，对转体系统的球铰接触面设置了接触单元，施加设计荷载，进行静力有限元分析，获得球铰的竖向应力，对转体系统的受力进行精细化分析，研究转体系统在承受上部结构荷载下的应力分布规律，并与规范公式进行对比分析，验证规范公式的计算精度。

1 球铰接触面应力规范计算方法

球绞的受力模型如图1所示，可将球铰接触面受力分为三类：

(1)沿球铰半径方向的径向力Nr。

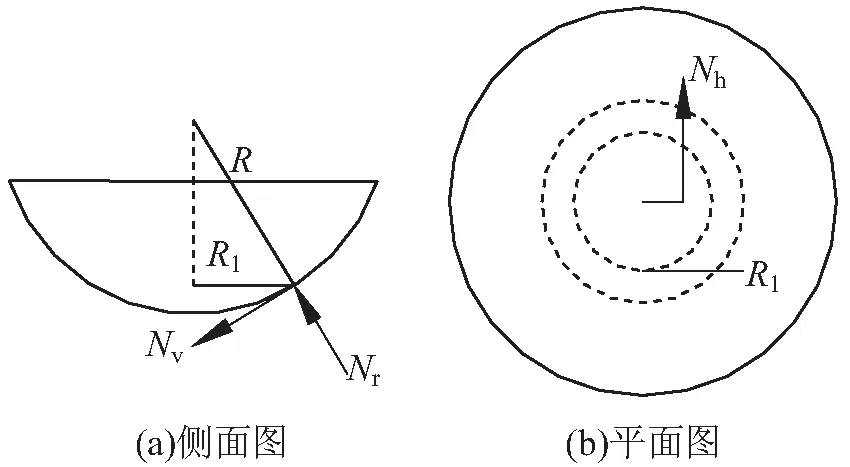
图1 球铰的受力模型

(2)通过球铰中心所在水平平面与球铰相切的摩擦力Nh。

(3)通过球铰中心所在垂直平面与球铰相切的摩擦力Nv。

规范《公路桥涵施工技术规范》(JTG/T F50-2011)(以下简称《规范》)中，计算球铰接触面应力的方法是：将上下球铰的接触面简化为平面，承受上部结构传来的荷载，并考虑应力均匀分布。其计算应力公式为：

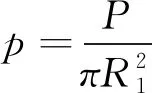
(1)

式中：p为接触压力；P为来自上部结构的荷载；R1为接触面半径。

2 工程概况及球铰接触面应力计算

延崇高速公路上跨康延铁路Q1K3+702.892处主桥采用2×60 m 预应力混凝土转体T构桥，转体段跨径均为55 m，两边跨端部现浇段长度均为4.78 m。转盘结构采用环道与中心支撑相结合的球铰转动体系，由转体下转盘、球铰、上转盘、转动牵引系统组成。转盘的混凝土采用C50，球铰采用GBT_700-2006规定的Q235B钢材。下转盘采用八边形平面形状，纵横尺寸为1 180 cm×1 742.6 cm，厚300 cm。转体球铰整体高度为822 mm，分上下两片。转台直径10.4 m，高度0.8 m。转体总重量W约为80 000 kN，启动时静摩擦系数按0.1、转动过程中的动摩擦系数按0.06计算，球铰平面半径为1.9 m。混凝土弹性模量采用3.45×104MPa，泊松比采用0.2，质量密度采用2 600 kN/m3；球铰弹性模量采用2.06×105MPa，泊松比采用0.3；转体系统侧面、平面和立面如图2所示。

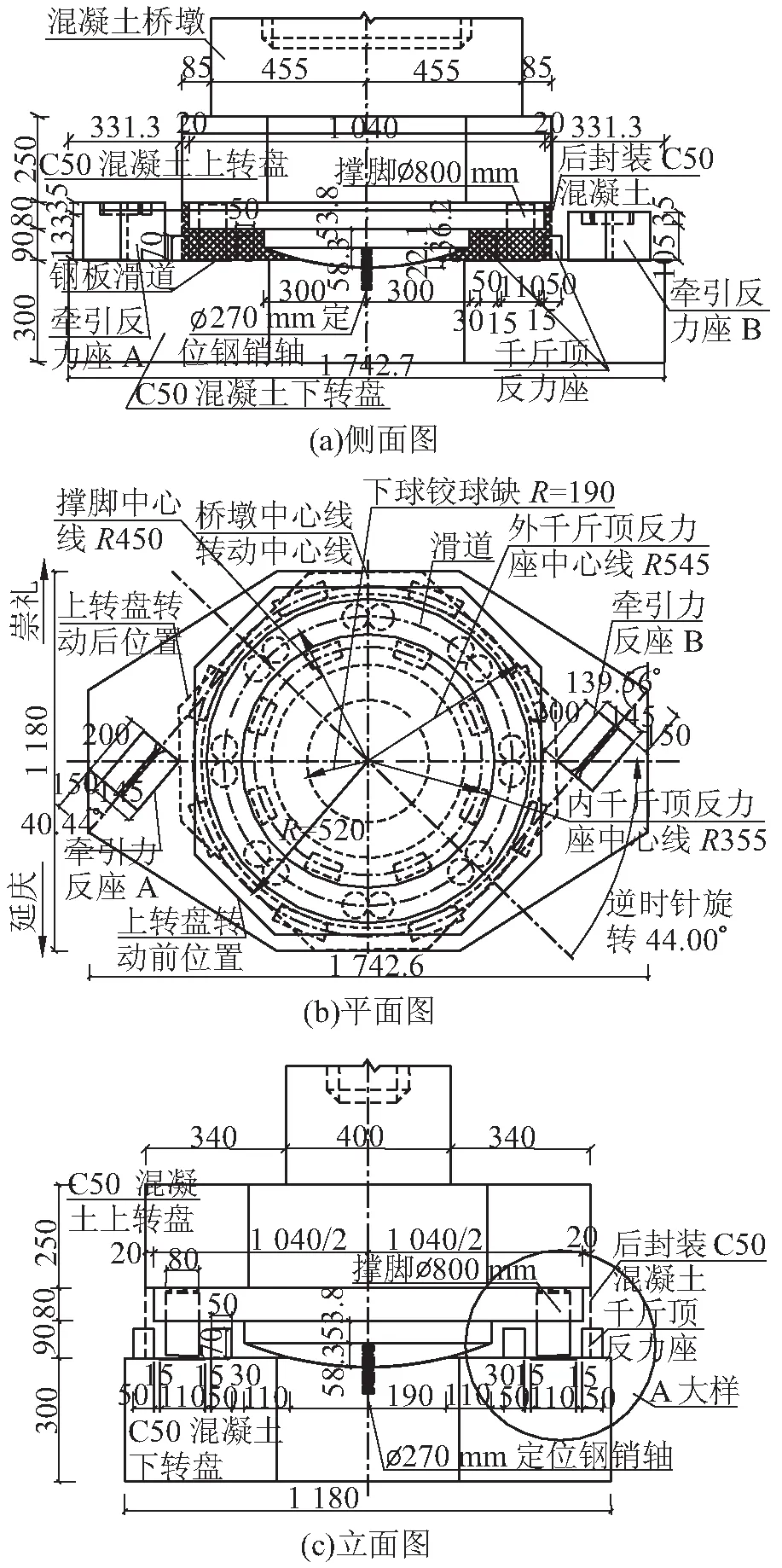
图2 转体系统结构(单位：cm)

根据《规范》计算公式(1)，可得设计所用的球铰接触面应力为：p=7.06 MPa。

3 有限元分析

3.1 建立有限元模型

采用ABAQUS2019进行建模，混凝土及定位轴采用实体单元，球铰采用壳单元，定位轴、球铰及球铰处上下转盘网格采用子网格进行细化，网格尺寸采用100 mm，其他部位网格尺寸采用1 000 mm，球铰与各自转盘采用绑定进行连接。定义上下球铰接触作用时，主面为下球铰，从面为上球铰。接触力学行为之切向行为选择罚摩擦，静摩擦系数为0.1，动摩擦系数为0.06，法向行为定义为硬接触。

荷载采用压力荷载的方法将转体结构重量按压力作用在上转盘顶部：p=0.768 MPa。

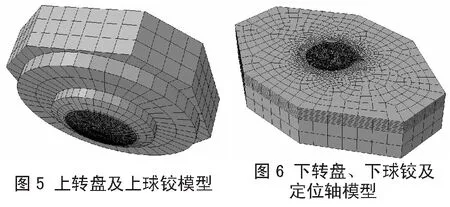
边界条件的施加是将下转盘底面的3个方向的平动和转动自由度进行约束。施加荷载与边界条件情况如图3所示，转体系统整体计算模型如图4所示，上转盘及上球铰模型如图5所示，下转盘、下球铰及定位轴模型如图6所示。

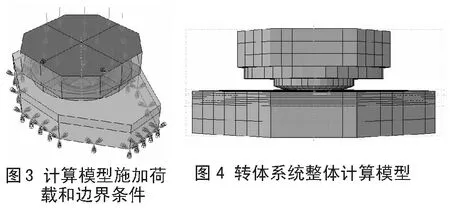
本文仅进行了静力线性分析，因此，混凝土和钢材的材料属性按《规范》进行取值，不考虑材料的破坏准则，并且未考虑钢筋与预应力钢筋的影响。另外，仅考虑了上部结构传下来的竖向荷载一种计算工况，对于转体转动等工况本文中尚未进行考虑。

3.2 有限元计算结果及分析

有限元的竖向应力结果如图7～图10所示。

从应力云图7可以看出：

(1)上转盘混凝土与球铰接触面间的竖向压应力分布从中间向球铰边缘方向逐渐增大。

(2)上转盘混凝土压应力数值整体较小，最大竖向压应力出现在接触面圆周边界上，其值为9.46 MPa，满足混凝土抗压强度设计值22.4 MPa的要求。

(3)上转盘混凝土在球铰外侧出现了拉应力，其最大值为0.47 MPa。

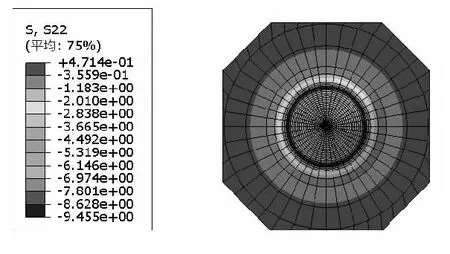
图7 上转盘竖向应力云图(单位：MPa)

从图8可以看出：

(1)上球铰竖向压应力分布规律与上转盘混凝土一致，从中心向边缘增大。

(2)上球铰的最大压应力出现在球铰边缘，其值为31.56 MPa。

(3)上球铰在靠近球铰边缘位置出现局部拉应力，最大值为25.79 MPa。

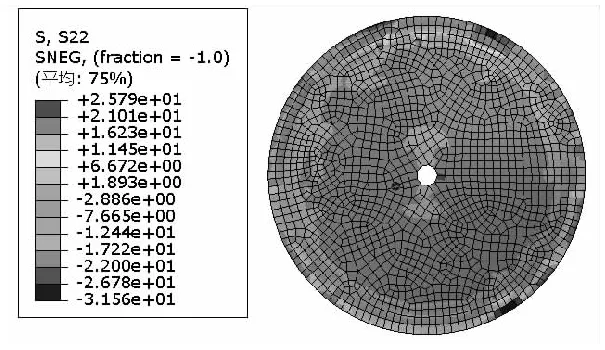
图8 上球铰底面竖向应力云图(单位：MPa)

从图9可以看出：

(1)下球铰竖向压应力分布规律与上球铰一致，从中心向边缘增大。

(2)下球铰的最大压应力出现在球铰边缘，其值为36.27 MPa。

(3)下球铰在靠近球铰边缘位置及转轴部位出现局部拉应力，最大值为10.80 MPa。

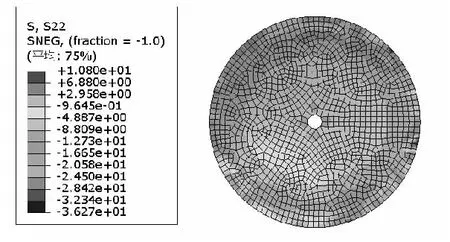
图9 下球铰顶面竖向应力云图(单位：MPa)

从图10可以看出：

(1)下转盘竖向压应力分布规律与下球铰一致，从中心向边缘增大。

(2)下转盘混凝土压应力数值整体较小，最大竖向压应力出现在接触面圆周边界上，其值为12.54 MPa，满足混凝土抗压强度设计值22.4 MPa的要求。

(3)下转盘混凝土在球铰外侧出现了拉应力，其最大值为0.56 MPa。

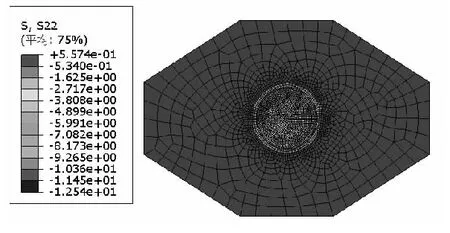
图10 下转盘竖向应力云图(单位：MPa)

采用下球铰最大压应力结果与《规范》公式结果比较，其相对误差为：

《规范》算法与有限元结果的最大值相差较大，低至80.53%。

4 结论

(1)在仅承受上部静力荷载下，转体系传统包括上、下转盘及上、下钢球铰竖向压应力沿球铰中心向边缘逐步增大，球铰边缘竖向压应力达到最大值。

(2)下球铰应力略大于上球铰应力，下球铰最大主压应力为36.27 MPa，上球铰最大主压应力为31.56 MPa，均小于钢制球铰容许应力215 MPa，而且应力图形不对称，其原因可能是球铰与转盘设置了绑定约束以及与网格划分有关。

(3)上、下转盘混凝土在球铰外侧出现了拉应力，上、下球铰在其边缘及转轴部位出现了拉应力。

(4)《规范》算法与有限元算法比较，《规范》公式结果比有限元结果的最大值低80.53%。