低速碰撞工况下的铸铝保险杠轻量化设计

谭继锦， 季天宇， 程文文， 解 宇

(合肥工业大学 汽车与交通工程学院，合肥 230009)

电动化、智能化、网联化和轻量化是目前汽车技术发展的总体趋势.其中，轻量化是关系到人类社会节能和环保的重要方向[1-2].保险杠是汽车的重要组成部分，主要作用是在车辆发生碰撞时，可以保护车身，是车辆被动安全的关键结构之一[3].在汽车整体轻量化的趋势下，保险杠的轻量化研究同样也很有必要.朱平、张宇等[4]采用高强钢和铝合金对车身主要覆盖件进行轻量化研究.刘海江等[5]以高强度片状模复合材料替代原保险杠零件的高强度钢材料进行轻量化设计.但仍然存在着零件多、结构复杂、装配环节多等问题.本文针对某一款电动轿车前保险杠，按精密熔模铸造工艺要求对保险杠系统进行一体化设计，用铸铝代替原高强度钢，简化了工艺，减少了装配环节，增加了结构强度，生产周期短且大批量生产时可有效降低制造成本，同时还达到了轻量化的效果.

1 轻量化材料选取

汽车轻量化主要有两大方式，①通过结构的改进，缩小零部件尺寸，使部件中空化、薄壁化;②使用轻量化的金属与非金属材料，进行材料替代[6].本文是从材料与结构两方面入手，进行材料替换与铸件一体化设计，结合保险杠的碰撞性能分析，满足设计性能要求.

铝添加一定的合金元素后，可获得具有良好铸造性能的铸造铝合金(ZL201A)，它具有成本低，强度高，延伸率良好等特点[7]，综合成本以及性能上考虑，选取ZL201A作为铸件材料，主要添加的化学成分为铜与少量的锰、钛元素，热处理状态为T5，铸造方式为精密熔模铸造.其性能与高强度钢对比见表1.

表1 ZL201A与高强度钢性能对比

2 原保险杠低速碰撞性能

2.1 碰撞仿真基本理论

保险杠的碰撞过程中属位移和应变都较大的非线性动力问题，利用有限元分析技术及动态显示求解技术进行碰撞仿真分析.涉及几何非线性问题的有限元法通常采用lagrangain增量法[8]，其平衡方程为：

(1)

上式实际上是虚功原理的一种表达，式中的各个积分项分别表示单位时间内系统的内力、惯性力、体积力和表面力所作的功.再加上在参考构型上节点相连的有限单元网格与随时间变化的运动轨迹，将单元里任意点的坐标用单元节点坐标插值，可得：

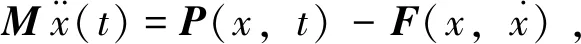
(2)

式中:M为总体质量矩阵；P为总体载荷矢量，由体力、面力、节点力等形成；F是由单元应力场的等效节点力的矢量(或称为应力散度)而组成.

考虑一个非线性结构的动力相应问题，动力学微分方程为

(3)

式中：M为结构的质量矩阵；C为结构的阻尼矩阵；K为结构的刚度矩阵；F′为外界作用力矢量；U为结构的位移矢量.

采用显示中心差分法计算，通过迭代求解，直到满足计算结束的条件[9].中心差分法对速度、加速度的导数采用中心差分替代，整理式(3)可得：

(4)

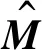
2.2 原保险杠有限元模型建立

将CATIA软件建立的保险杠三维模型，抽取中面后导入到Hyperworks中.清理错位和小孔，压缩相邻曲面之间的边界，消除不必要细节，提高整个划分网格的速度和质量，减少计算误差.

按照法规标准中4 km/h正面碰撞与2.5 km/h的60°偏置碰撞的要求建立有限元模型，如图2所示，并导入Ls-dyna中计算.

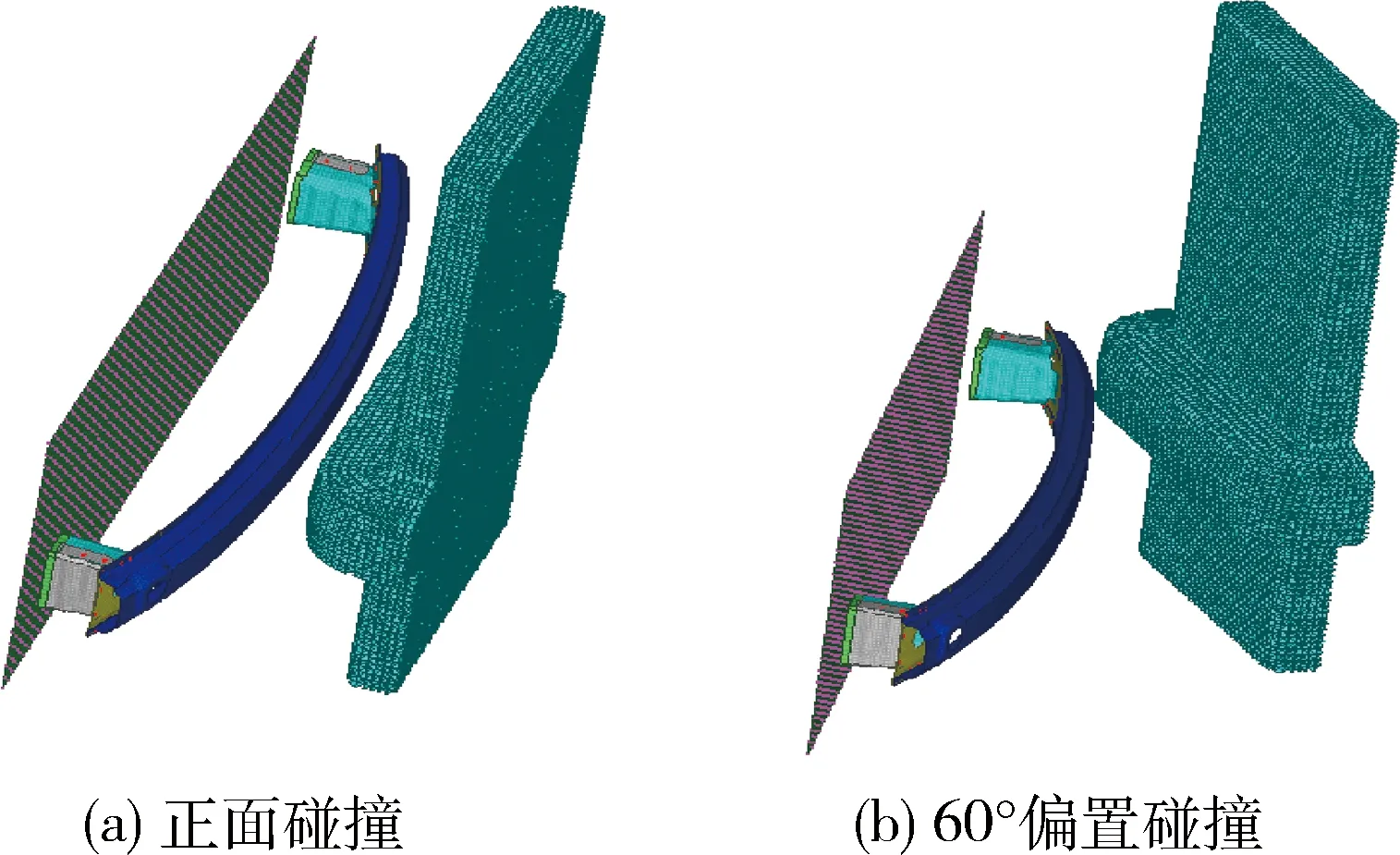
图2 两种碰撞形式的有限元模式

2.3 原保险杠低速碰撞响应特性

保险杠在低速碰撞的过程中，其最大变形量必须控制在一定的范围内才可以保证保险杠所连接的车身不受损伤.考虑到保险杠外板与吸能泡沫等元件的影响，该款车的最大许可纵向位移为50 mm，若低于该数值，则可以保证保险杠碰撞后车身结构不受损.

原保险杠摆锤正面碰撞位移云图如图3所示.由图可知，在仿真过程中原保险杠的变形主要集中在前梁的中间部位.其纵向最大位移为32.68 mm，未超过许可位移，符合要求.

图3 保险杠正面碰撞应变

原保险杠碰撞过程中能量变化如图4所示.摆锤的起始动能为725.2 J，在20 ms左右经过正碰后，75 ms左右保险杠系统吸能达到最大，吸能量为541.2 J，吸能百分比达到74.6%，130 ms碰撞结束，系统趋于稳定，吸能效果良好.

图4 保险杠正面碰撞吸能特性

60°偏置碰撞应变云图如图5所示.从图中可知，60°偏置碰撞时，原保险杠系统发生变形主要位置在前梁与吸能盒连接处，位移大小为8.54 mm.

60°偏置碰撞过程中，碰撞系统的能量变化状况如图6所示.系统初始总能量(摆锤的初始动能)为265.2 J.50 ms左右保险杠吸收能量达到最大，为70.9 J，占总能量的26.7%，75 ms碰撞完全结束.

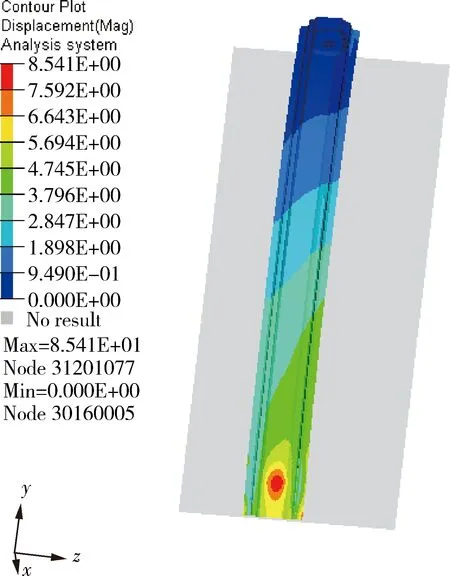
图5 保险杠60°偏置碰撞应变

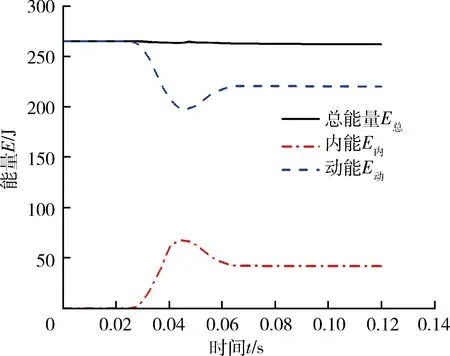
图6 保险杠正面碰撞吸能特性

3 铸铝保险杠设计

3.1 铸铝保险杠前梁设计

常见的主梁截面类型有“弓”形，“凸”形以及“日”形等[10]，考虑到简化铸造工艺实现的复杂程度，这里采用半封闭的凸形结构作为保险杠的截面形状，如图7所示.铸件壁厚以零件最大轮廓尺寸为参考，满足最小壁厚要求，通过查阅HB 963-2005铝合金铸件规范，最小壁厚应为2 mm.前部曲面应合理设置加强肋，提高强度，如图8所示.

图7 前梁拓截面

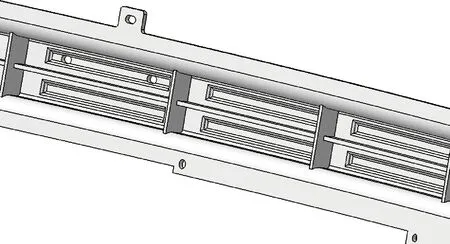
图8 最终前梁结构

3.2 吸能盒设计

常见的吸能盒单胞结构有正方形、长方形、圆形、正六边形和正八边形结构，为保证充分压溃，以刚性墙对这5种结构(长度120 mm，壁厚3 mm，界面周长为300 mm，材料为ZL201A)施加16 km/h的碰撞速度，刚性墙是形状为边长200 mm的正方形，只能沿X方向上平动，质量设为整车质量，如图9所示.

图9 吸能盒单胞结构

计算所得碰撞参数见表2.从表中可以看出截面形状对单胞结构的吸能特性影响很大，截面为多边形时，边数的增大能使截面的吸能特性有所增加，但边数的增加会导致冲击力的震荡频率和振幅增大，综合考虑各参数，正六边形吸能盒吸能特性最佳.

表2 不同类型单胞结构碰撞性能

内部多胞结构中，能否很好吸能取决于内部隔板是否可以对外壁的横向位移产生很好的限制作用.目前常见的多胞结构壁的连接方式为直角连接，T形连接和十字形连接，十字形连接性能最优，T形连接其次[11].由于考虑铸件采用十字形连接方式会导致中间区域浇注缩孔且不易补缩，这里采用T型作为内外壁的连接方式，如图10所示.

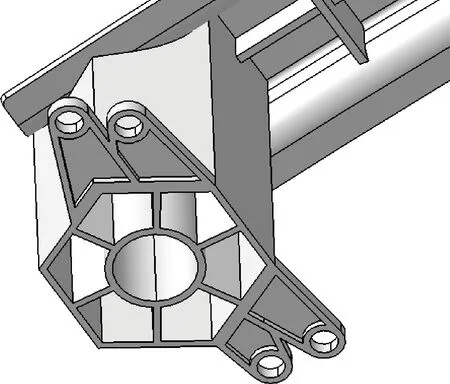
图10 最终吸能盒结构

4 铸铝保险杠厚度优化

4.1 优化变量选择

与传统冲压薄壁件的制造工艺相比，精密熔模铸造工艺的特点是可以根据需要在不同的平面设置任意数值的壁厚[12].本文取保险杠前梁壁厚T1、保险杠前梁布置的加强筋厚度T2和吸能盒壁厚T3，3个厚度值作为设计变量，为达到轻量化的最终目标，以保险杠低速碰撞前梁的最大入侵位移、正碰时最大吸能量和偏置碰撞最大吸能量为约束，以保险杠质量最小为优化目标，采用中心复合试验设计对保险杠的各个变量进行优化设计.吸能盒壁厚设计参数如图11所示，其初始值及上下限设置见表3.

表3 变量初始值及其上下限

图11 参数壁厚示意图

4.2 中心复合试验设计

中心复合试验设计的核心思想:设有k个设计因素，使用x=[x1,x2,...,xk]来表示每个因素水平的编码形式，由立方点、轴点与中心点3个部分来构成一组中心复合试验设计.2k个立方点或角点，其中xi=1或-1，i=1，2，…，n；2k个轴点或星点，xi=a或-a，i=1，2，…，n；nc个中心点，xi=0，i=1，2，…，n.

一组中心复合试验设计的总的样本点数目为M=2k+2k+nc.在k个因素下，使a=2k/4能够让样本点具有旋转性，合理地选择中心点与试验次数，能够让中心复合试验设计拥有正交性，此法经常应用于响应面法的研究中[13].

4.3 优化及结果分析

根据在前文中已确定的设计变量、优化目标与约束条件，构建数学模型如下:

式中：M为铸铝保险杠质量；X为正碰最大入侵位移，以原保险杠最大入侵位移(32.68 mm)来约束，E1，E2分别为正碰与偏置碰撞的最大吸能量，同样以原保险杠性能来约束，T1，T2，T3分别为优化的设计变量.

按照中心复合试验设计的各组变量进行仿真计算，计算结果见表4.

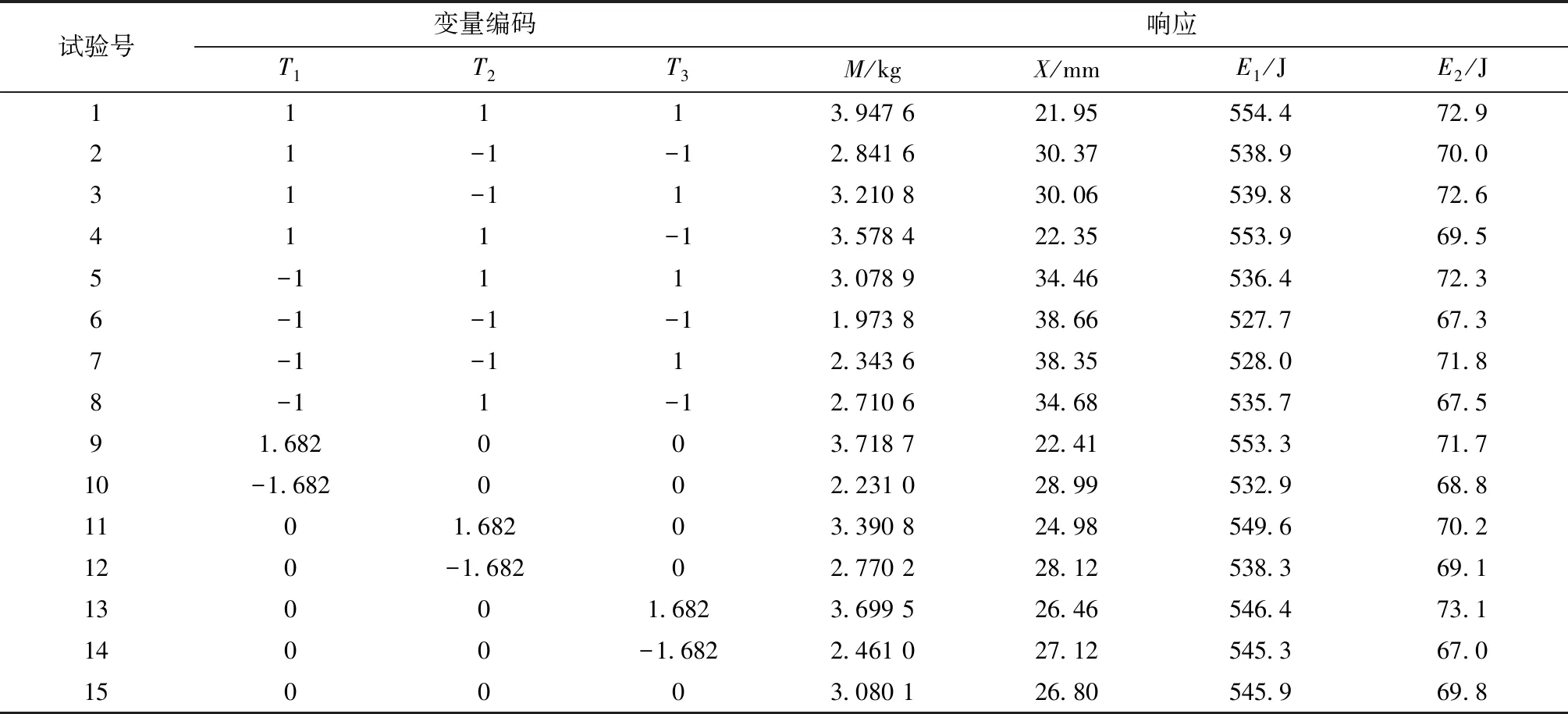
表4 中心复合设计及其响应

将在试验设计后数值模拟得出的结果导入isight数值优化软件，通过移动最小二乘法来确定系数，建立其响应面模型，其模型函数为

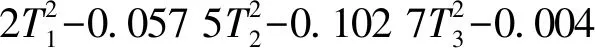
在isight中利用自适应响应面法对响应面模型进行优化，在45次迭代后达模型收敛，如图12所示(以T2为例)，并将优化结果与按照最优点处的设计变量值进行仿真的结果对比，见表5.从表中可以看出，保险杠的优化结果与仿真验证结果误差很小，总体近似精度较高.

表5 优化结果与仿真对比

图12 T2迭代收敛图

通过对比原保险杠与设计的铸铝保险杠的各项性能如表6所列，铸铝保险杠的正碰与偏执碰撞的吸能量与原保险杠相当，但最大入侵位移小于原保险杠，同时,其质量仅有2.924 5 kg，减重比例达到35%，不但性能方面有所提升，轻量化效果也很显著.

表6 原保险杠与铸铝保险杠性能对比

4 结 论

从保险杠的碰撞性能角度出发，使用铸铝件代替高强度钢进行一体化设计，在Hyperworks中建立原保险杠有限元模型，导入LS-dyna计算，对原保险杠的纵向位移，吸能量进行评价，并以此为约束，对铸铝保险杠进行厚度优化，优化后的保险杠轻量化效果明显，减重比例达到35%.相关研究方法对于保险杠等部件的轻量化研究及铸件在车身上的应用具有一定的实践意义.