在幺模矩阵加密方法下的安全外包算法*

张胜霞，田呈亮,2+

1.青岛大学 计算机科学技术学院，山东 青岛266071

2.中国科学院 信息工程研究所，信息安全国家重点实验室，北京100093

1 引言

安全外包计算，作为一个非常重要的服务，已经变得越来越流行。资源受限的客户端独立求解是非常困难且代价昂贵，云计算[1-2]对于资源有限的客户端进行大规模的数据计算提供了一个高效且经济的服务,因此客户端需要将大量的计算任务外包给云服务器[3-5]。安全外包计算的最终目标是使客户端的计算成本最小化，并保持原始数据的机密性和完整性。一般来说，云服务器并不是完全安全可靠的，如果将包含敏感信息的原始数据发送到云端，将会危及原始数据的完整性。因此，安全外包计算方法至少应该满足以下要求：（1）正确性，对于一个诚实的云服务器，该算法可以使客户端正确地获得想要的结果。（2）输入/输出隐私性，算法应保证计算任务的实际输入和输出对云服务器是不可见的。（3）可验证性，算法必须确保客户端能够以不可忽略的概率验证从云服务器返回的结果的正确性。（4）高效性，在外包算法中，客户端的本地计算开销应该远远小于其自身对原始任务的计算开销。

矩阵作为一种基本的数学对象，广泛应用于科学和工程计算领域。许多不同的实际问题可以归结为矩阵计算问题。在物理的每一个分支，包括经典力学、光学、电磁学、量子力学和量子电动力学，矩阵被用来研究物理现象，如刚体的运动[6]。在计算机图形学中，它们被用来操作3D 模型并投射到二维平面上。在图像处理中[7-8]，通过矩阵操作对图像进行去除噪声、增强、复原、分割、提取特征等处理。在概率论和统计学中，随机矩阵被用来描述概率集合，例如，它们被用在谷歌搜索系统中对页面进行排序的PageRank 算法中[9]。矩阵在经济学中被用来描述经济数据关系模型。因此，对于基本矩阵运算的算法，如矩阵乘法计算（matrix multiplication computation，MMC）、矩阵求逆计算（matrix inversion computation，MIC）和矩阵行列式计算（matrix determinant computation，MDC），已成为现代科学计算的重要组成部分。从复杂性的角度来看，MMC、MIC 和MDC 等基本算法具有相同的时间复杂度O(n3)（对于n×n的矩阵），并且已知最快的算法的渐近时间复杂度为O(n2.373)。然而，随着大数据时代数据生成量的指数增长，现实问题中需要处理的矩阵往往非常大，通常有数十万个条目[10-12]。因此，为矩阵操作设计安全、可验证、高效的外包协议成为资源受限客户的迫切需求。

近年来，由于大规模矩阵运算在各个领域的广泛应用，许多学者提出了大量将矩阵相乘[13-15]、矩阵特征多项式[16-17]等不同矩阵操作外包的协议。

首先，关于矩阵乘法，在1998 年，Atallah 等人[18]最先提出了MMC 和MIC 的外包方案，他们采用了随机置换矩阵来加密。在2008 年，Benjamin 和Atallah[19]利用同态加密的性质又设计了MMC 的外包协议。在2010 年，Atallah 和Frikken[20]设计了一个基于Shamir秘密共享的矩阵乘法外包协议，该方案只需要一台云服务器。在他们的协议中，运行的时间成本为O(t2n2)，其中t是Shamir 秘密共享方案的一个阈值。换句话说，客户端计算至少需要4t+2 次矩阵乘法，这会增加客户端计算负担。在2012 年，Mohassel[21]利用多种现有的同态加密方案设计了MMC 的外包算法，并设计了一种通用的验证方法。Fiore 等人[22]和Zhang 等人[23]设计了公开验证的方法，让第三方来验证云返回结果的正确性。最近，Lei 等人[24]提出了一种利用蒙特卡洛验证的方法安全外包MMC 的协议，该方案采用与文献[18]相同的随机置换矩阵。客户端的计算时间是O(n2)，但是原矩阵的零元素的数目会暴露给云服务器。

其次，关于安全外包MIC 的协议，Lei等人[25]利用与外包矩阵乘法方案[20]相同的加密方法来设计MIC的协议。这样，原始矩阵的每个元素的位置都被随机地重新排列，并进一步受到多个随机值的保护。但是，原矩阵的零元素的数目同样会暴露给云服务器。

最后，行列式计算在科学和工程领域有着极其广泛的应用。Lei 等人[26]通过LU（lower-upper）分解给出了一个方案，作者通过添加零矩阵块来保护零元素的数目。虽然零元素的数目得到了保护，但是原矩阵的维数从n增加到了n+m，其中m×n是零矩阵块的维数，这样客户端本地的计算量会变大。

本文针对上述保护输入矩阵中零元素数目的问题，提出了一种新颖的加密方法。更具体地说，本文的协议通过使用幺模矩阵来保护零元素的数目，同时维护数据的输入输出隐私，实现结果的可验证性。此外，本地端的计算开销得到了很大的节省，就复杂度而言，客户端的计算开销从O(n3) 降低到了O(n2)。本文所提出的幺模矩阵的加密方法有很广泛的适用性，除了本文所讨论的MMC、MIC 和MDC 加密外，还可以应用到外包其他矩阵操作中。

2 问题描述

2.1 系统模型

如图1 所示，安全外包计算模型包括两个实体：资源受限的客户端和有着强大计算资源和特殊软件的云服务器。客户端想要通过外包给云端进行大规模的矩阵运算，为了保护输入隐私，首先必须使用密钥加密原始矩阵。然后，把加密后的矩阵发送给云。云通过调用大量的资源完成计算后，将计算结果返回给客户端。客户端一旦收到返回的结果，将会使用密钥解密。同时，客户端必须检查结果是否正确。如果是，则接受；否则，拒绝。

2.2 安全性定义

安全外包算法需要满足以下四个要求：

（1）正确性：只要云服务器是诚实的，客户端就会收到一个有效的输出，通过解密和验证，得到正确的结果。

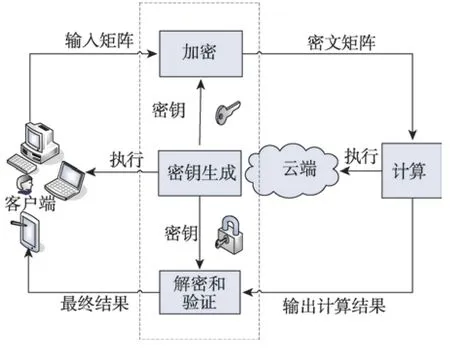
Fig.1 System model图1 系统模型

（2）输入输出隐私性：算法需要隐藏原始数据的隐私信息。一方面，云不能获得任何原始数据的隐私信息；另一方面，正确的结果对云也是保密的。

（3）可验证性：客户端必须成功验证云服务的正确结果，准确检测错误结果。

（4）高效性：客户端外包的计算时间远远小于其不外包时在本地的计算时间。

3 预备知识

3.1 置换映射

置换[27]在群理论和组合学中有着广泛的应用。置换映射是有限集上的双射，可写成如下：

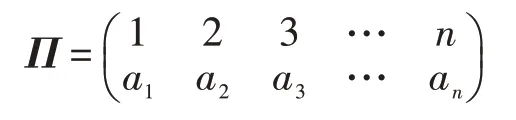
其中，ai是一个从1到n的整数，且ai≠aj,i,j=1,2,…,n。置换映射可以写成轮换和对换两种形式。根据对换的数目，置换分为奇置换和偶置换。给定一个置换Π，sgn(Π)定义为：

3.2 置换矩阵

给定一个有限集S={1,2,…,n}和一个置换映射Π，所产生的置换矩阵[28]P为，其中αi为随机数，Kronecker delta 函数δx,y被定义为：

置换矩阵P的行列式为：

注：当置换矩阵P为时，det(P)=sgn(Π)=±1。

3.3 幺模矩阵

定义 一个n×n的矩阵U是幺模矩阵[29]当且仅当且其行列式的绝对值模q同余1，表示为|det(U)|=1 modq。

幺模矩阵的一个简单性质[30]是，一个幺模矩阵的逆也是幺模矩阵。本文中幺模矩阵U的结构为：

其中，对角位置上的(u1,u2,…,ut-1)是一系列2×2 的幺模矩阵。当n是偶数，ut也是2×2 的幺模矩阵；当n是奇数，ut是一个3×3 的幺模矩阵。本文设计的协议中，ut的行列式均为1，在预处理阶段，利用扩展的欧几里德算法快速地生成了这些幺模矩阵ut。

3.4 相关符号

本文所提到的缩写形式的定义如表1 所示。

Table 1 Definition of abbreviation表1 缩写定义

4 外包矩阵操作的算法

4.1 计算任务描述及基本思想

给定一个矩阵，客户想要计算行列式、逆阵和与另一个矩阵相乘。解决这些问题的经典方法是用高斯消去法、凯莱-哈密顿法等[31]。这些算法一般都需要O(n3)的时间复杂度。由于密码应用中涉及的维度通常非常大，资源有限的客户很难进行如此昂贵的操作。在这种情况下，客户端可以通过安全外包计算来完成这一任务。

一般来说，如果对于两个n×n的矩阵相乘，其复杂度为O(n3)，但是如果其中有一个是稀疏矩阵，那么复杂度为O(n2)。基于这种启发，本文通过引入置换矩阵和幺模矩阵来加密原始矩阵。任何一个n×n的矩阵和一个n×n置换矩阵相乘复杂度为O(n2)，同样和一个n×n的幺模矩阵相乘复杂度仍然为O(n2)。利用这一特性，实现对原始矩阵的加密。然而，对于安全外包协议来说，矩阵中零元素的位置和数目是非常重要的。如果两者都不受保护，云可能会获取大量的敏感信息，进而通过自身强大的资源获得正确的结果。

通过对输入矩阵乘随机置换矩阵，每个元素的位置将会被随机打乱。换句话说，零元素的位置也被打乱。然而，零元素的数目仍然保持不变。因此，进一步通过乘随机幺模矩阵来改变零的数目，同时仍然保持一定的高效性。密钥是随机置换矩阵和幺模矩阵。密钥幺模矩阵的一般结构如式（1）所示。

4.2 安全外包矩阵相乘（MMC）的算法

给定两个矩阵X,，外包矩阵相乘的算法包含以下5 个步骤：

（1）密钥生成

①客户端随机地生成3个幺模矩阵U1、U2和U3。

②客户端生成3 个随机置换矩阵P1、P2和P3，,k=1,2,3，Πk是一个随机置换。

（2）加密

①客户端使用随机置换矩阵，首先计算X′和Y′。

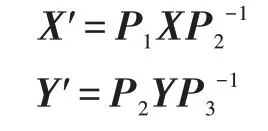
②客户端使用密钥幺模矩阵，然后计算X″和Y″。

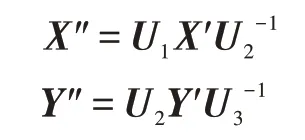
客户端随机地发送X″和Y″给云服务。

（3）云计算

当云接收到加密后的矩阵X″ 和Y″ 时，计算Z″=X″Y″，并将结果Z″返回给客户端。

（4）解密

当客户端接收到云返回的结果Z″，客户端进行解密：

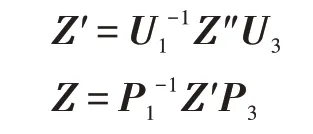
则Z是X和Y相乘的结果。

（5）结果验证

客户端对于解密后的结果Z进行验证，通过计算P=X×(Y×r)-Z×r，r是一个随机0-1 列向量，任意非零向量P意味着验证失败。

4.3 安全外包矩阵逆阵（MIC）的算法

（1）密钥生成

①客户端生成两个幺模矩阵U1和U2。

②客户端生成两个随机置换矩阵P1和P2，,k=1,2,3，Πk是一个随机置换。

（2）加密

①客户端使用随机置换矩阵，首先计算X′。

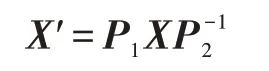
②客户端使用幺模矩阵，计算X″。

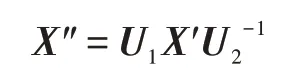
客户端发送X″给云服务端。

（3）云计算

当云接收到加密后的矩阵X″时，计算其逆矩阵Z″=(X″)-1，并将其返回给客户端。

（4）解密

当客户端收到来自云端的Z″时，进行解密：

则Z为原始矩阵X的逆矩阵。

（5）结果验证

客户端对解密后的矩阵进行验证，通过计算P=X×(Z×r)-Ι×r，r是一个随机0-1 列向量。I是一个单位矩阵。任何非零向量P意味着验证失败。

4.4 安全外包矩阵行列式（MDC）的算法

（1）密钥生成

①客户端生成4 个幺模矩阵U1、U2、U3和U4。

②客户端生成4 个随机置换矩阵：

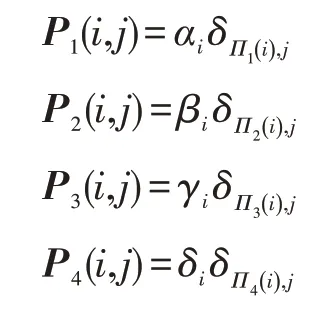
其中，Πk是随机置换，αi、βi、γi和δi是随机数。

（2）加密

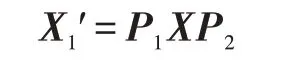
（3）云计算

（4）结果验证和解密

如果等式成立，视等式右边或者左边的结果为正确结果。否则，客户端输出“⊥”。

5 安全性分析

定理1在单个云服务器模型中，安全外包MMC协议是正确的、安全的和可验证的。

证明（1）MMC 协议是正确的。

如果云是诚实的，那么客户端可以成功解密收到的结果Z″并且得到的结果Z总是正确的。值得一提的是X″和Y″由给出。诚实的云在收到客户端发送的X″ 和Y″ 时会计算Z″=X″Y″。然而：

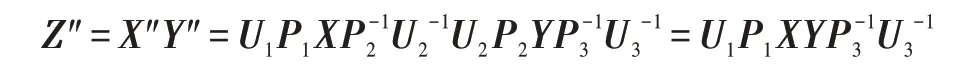
（2）MMC 协议是安全的。

MMC 协议可以保护输入隐私，因为云不能从加密后的矩阵X″和Y″中获得原始矩阵的任何信息。原始矩阵X（Y）的加密分为两个阶段。

阶段1 原始矩阵X盲化成X′ 乘以置换矩阵，。

阶段2 矩阵X′盲化成X″乘以幺模矩阵，X″=。

①在阶段1 中，矩阵X中每个元素的位置在随机置换矩阵的作用下重新排列了。如果恶意的云想从X′中恢复X需要猜中2n!种情况的排列。

②在阶段2 中，由于阶段1 仅盲化了零元素的位置，因此这一步需要盲化零元素的数目。通过在两边乘幺模矩阵，X″ 和X的零元素的数目会随之改变，有可能增加也有可能减少。这样，即使是拥有强大的计算能力的恶意的云也无法再获得它的数目，因为在矩阵X″中零元素的分布没有任何规律。

根据上面的分析，如果没有每个阶段密钥，云是无法从X″中获得原始输入矩阵X的任何数据。这样，MMC 协议被认为实现了安全性，因此输入隐私得到了保护。

（3）MMC 协议是可验证的。

解密后的结果进行第5 步的验证，验证算法重复l次。在本文的协议中l=50，这个值是在强抵抗性和高效率之间的一个阈值。 □

定理2在单个云服务器模型中，安全外包MIC协议是正确的、安全的和可验证的。

证明（1）MIC 协议是正确的。

如果云是诚实的，那么客户端可以成功解密收到结果Z″并且得到的原始结果X-1（相当于Z-1）总是正确的。值得一提的是X″是由给出。诚实的云会计算其逆矩阵。然而，(X″)-1=。把(X″)-1记作Z″。客户端解密通过计算，可以立即得到Z-1=X-1。也就是说MIC 协议是正确的。

（2）MIC 协议是安全的。

MIC 协议可以保护输入隐私，因为云不能从加密后的矩阵X″中得到原始矩阵的任何信息。原始矩阵X的加密分为两个阶段。

阶段1原始矩阵X盲化成X′ 乘以置换矩阵，。

阶段2矩阵X′盲化成X″乘以幺模矩阵，X″=。

①在阶段1 中，矩阵X′中每个元素的位置在随机置换矩阵的作用下重新排列了。如果恶意的云企图从X′中恢复X，需要猜对2n!种置换。

②在阶段2 中，因为阶段1 没有保护零元素的数目，这一步将会实现。通过在两边乘幺模矩阵，X″和X的零元素的数目会随之改变，有可能增加也有可能减少。这样，即使是拥有强大的计算能力的恶意的云也无法再获得它的数目，因为在矩阵X″中零元素的分布没有任何规律。

根据上面的分析，如果没有每个阶段密钥，云是无法从X″中获得原始输入矩阵X的任何信息。这样，MIC 协议被认为实现了安全性，因此输入隐私得到了保护。

（3）MIC 协议是可验证的。

解密后的结果会进行第5 步的验证，验证算法重复l次。在本文的协议中l=50，这个值是在强抵抗性和高效率之间的一个阈值。 □

定理3在单个云服务器模型中，安全外包MDC协议是正确的、安全的和可验证的。

证明（1）MDC 协议是正确的。

如果云诚实地遵守协议，则det(X) 可由或者得到，其中和是云返回的结果。det(P1)、det(P2)、det(P3)和det(P4)可由客户端简单地计算出来。如果云是诚实的，那么在第4 步中的解密过程总会得到正确的结果。因为，可得如下关系：

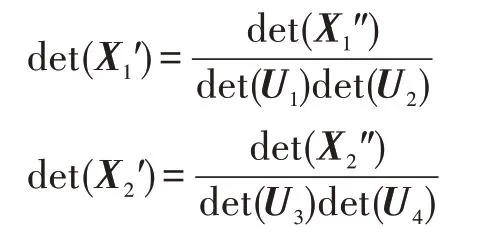
又根据det(U1)=det(U2)=det(U3)=det(U4)=1，进而可以得到：

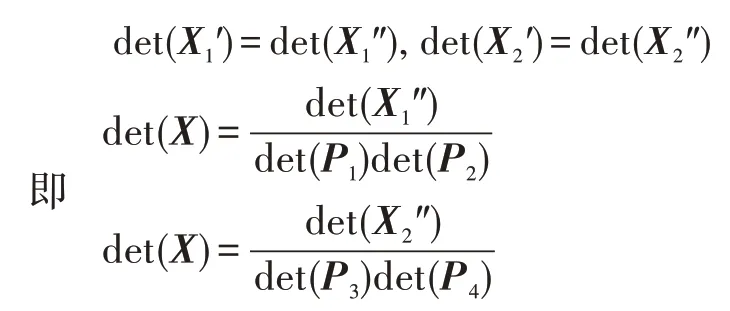
这表明解密过程总是能够满足正确的结果，因此本文的协议是正确的。

（2）MDC 协议是安全的。

由于云无法从密文矩阵X1″和X2″中获取原始矩阵的任何信息，因此MDC 协议可以保护输入隐私。原始矩阵X分为两个阶段加密。

阶段1原始矩阵X盲化成X′ 乘以置换矩阵，。

阶段2矩阵X′盲化成X″乘以幺模矩阵，。

①在阶段1，矩阵X中的每一个元素都在随机置换下重新排列。云端若想从中恢复X，需要猜对4n!种置换且要猜对系数(α1,α2,…,αn),(β1,β2,…,βn),(γ1,γ2,…,γn),(δ1,δ2,…,δn)。

根据以上分析，如果没有每个阶段的密钥，云端就无法从X″中恢复X。MDC 协议被认为是实现了安全性，因此输入隐私得到了保护。

（3）MDC 协议是可验证的。

6 实验评估

在这一章中，对于安全外包MMC、MIC 和MDC算法提供了理论和实验分析。在理论方面，针对算法不同阶段的计算时间和是否保护零元素数目的问题，对Atallah、Lei 和本文的方案进行了对比，如表2所示。表中最后一列表示是否保护零元素的数目，可见本文设计的3 个算法都保护了零元素的数目，同时客户端本地计算的时间复杂度为O(n2)。而且与其他方案不同的是，本文的MDC 算法的验证时间只需要O()1 。除此之外，本文设计的3 个协议都是基于Fq的代数结构。

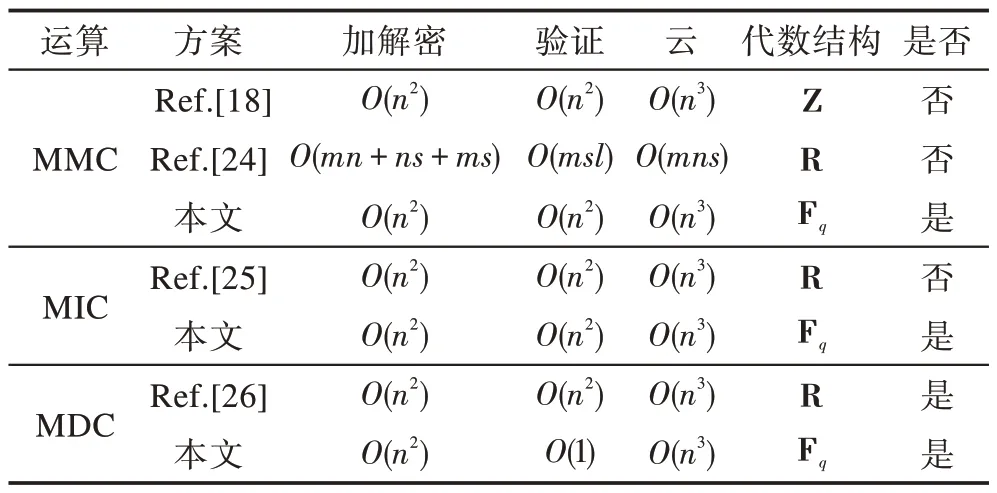
Table 2 Comparison of different schemes表2 各方案的比较

对于所提出的3 个安全外包算法进行了实验评估。实验是在装有2.70 GHz 英特尔i5 处理器和4 GB内存的Ubuntu 系统上进行的。本文中选择参数q为251，相应地记录了3 个算法在不同维数和不同加密阶段所需要的计算时间，如表3、表4 和表5 所示。随着矩阵维数n的增加，客户端不外包的计算时间toriginal不断增大，外包计算的时间tclient也相应地变大。但两者相比而言，tclient要远远小于toriginal。也就是说外包计算所节省的时间效率随着矩阵规模的增大越来越大。当维数n为2 000 时，外包MMC 可以获得9 倍以上的效率。当维数n为1 000 时，外包MIC 可以获得20 倍的效率。同样，当n为5 000 时，外包MDC 可以获得超过9 倍的效率。

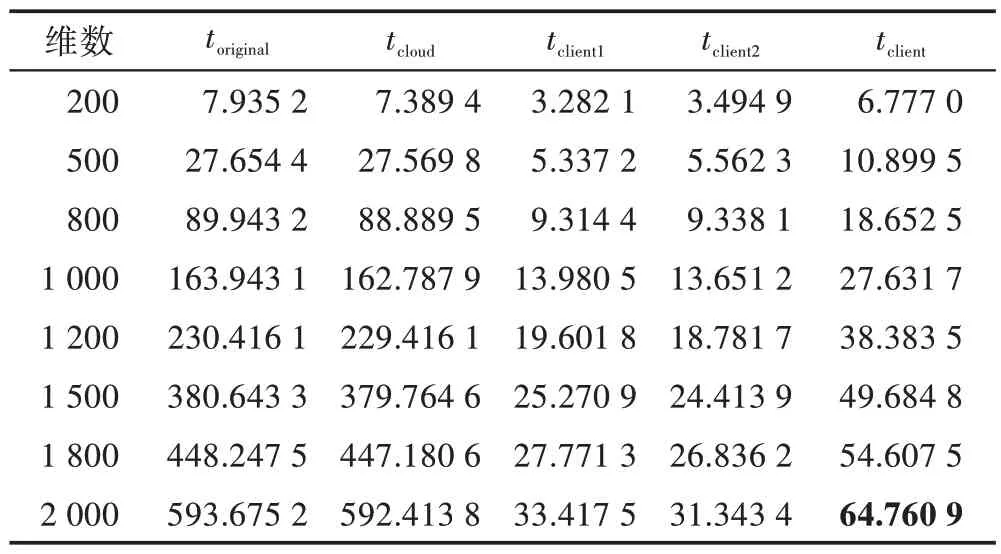
Table 3 Running time of each stage of protocol MMC in different dimensions表3 协议MMC 各阶段在不同维度下的计算时间 s

Table 4 Running time of each stage of protocol MIC in different dimensions表4 协议MIC 各阶段在不同维度下的计算时间 s

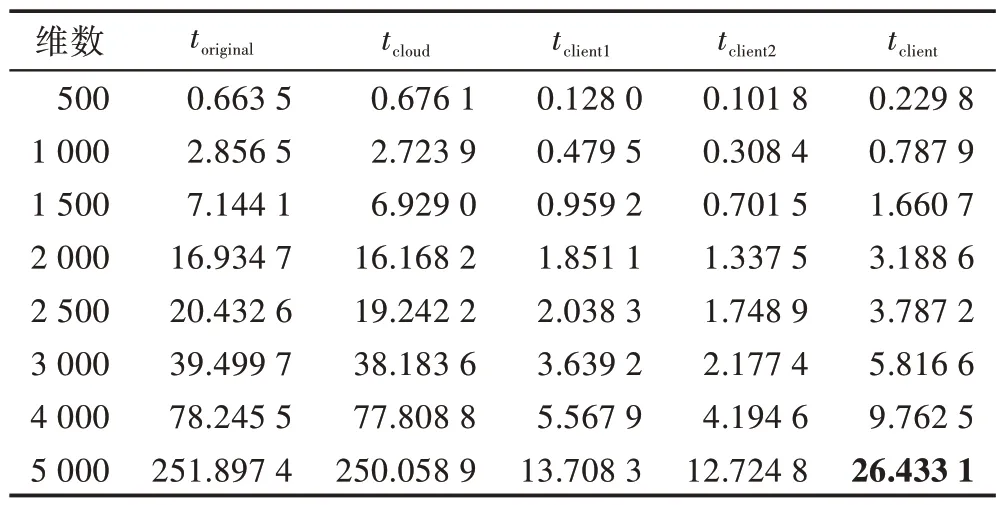
Table 5 Running time of each stage of protocol MDC in different dimensions表5 协议MDC 各阶段在不同维度下的计算时间 s

外包MMC 算法和不外包的时间比较如图2 所示。toriginal是不外包MMC 时的本地计算时间，tclient是外包MMC 的计算时间。随着矩阵规模的增大，两者的差距越来越大。外包MMC 所需要的时间远远小于不外包所需要的时间。这说明，外包MMC 算法具有高效性。

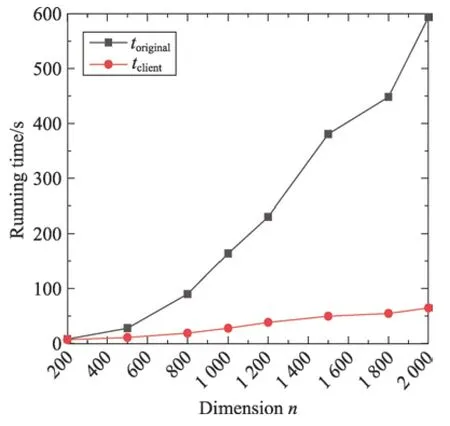
Fig.2 Comparison between outsourcing MMC and non-outsourcing computing图2 外包MMC 和不外包计算的比较

外包MIC 算法和不外包的时间比较如图3 所示。toriginal是不外包MIC 时的本地计算时间，tclient是外包MIC 时的计算时间。随着矩阵规模的增大，两者的差距越来越大。外包MIC 所需要的时间远远小于不外包所需要的时间。这说明，外包MIC 算法具有高效性。

外包MDC 算法和不外包的时间比较如图4 所示。toriginal是不外包MDC 时的本地计算时间，tclient是外包MDC 时的计算时间。随着矩阵规模的增大，两者的差距越来越大。外包MDC 所需要的时间远远小于不外包所需要的时间。这说明，外包MDC 算法具有高效性。

Fig.3 Comparison between outsourcing MIC and non-outsourcing computing图3 外包MIC 和不外包计算的比较

Fig.4 Comparison between outsourcing MDC and non-outsourcing computing图4 外包MDC 和不外包计算的比较

图5 和图6 中的client speedup 表示客户端的加速比，是toriginal和tclient的比值，图5 和图6 分别对外包MMC 和MIC 的client speedup 与Lei等人的client speedup 做了比较。图5 表明，本文的加密方法在外包MMC 时客户端所获得的speedup 要略高于Lei 的speedup。图6 表明，本文外包MIC 所获得的speedup 与Lei 的speedup 相差较大，说明外包MMC和MIC 减少了客户端的计算开销。因此，本文的外包算法具有高效性。

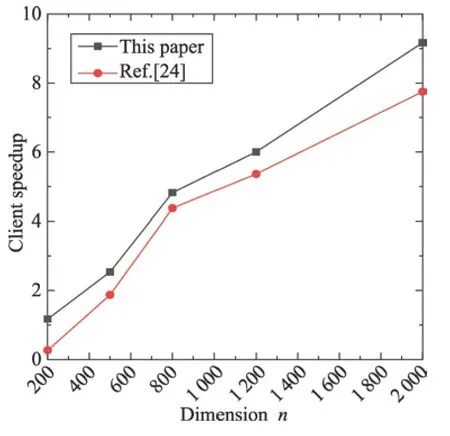
Fig.5 Comparison of client speedup of outsourcing MMC图5 外包MMC 的客户端speedup 的比较

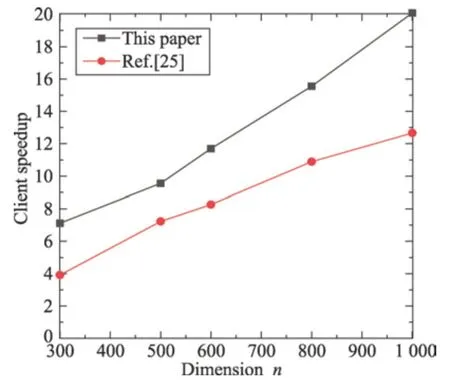
Fig.6 Comparison of client speedup of outsourcing MIC图6 外包MIC 的客户端speedup 的比较

7 结束语

本文设计了一种将矩阵相乘、矩阵求逆和行列式外包给云的算法。通过在置换矩阵的基础上引入幺模矩阵的加密方法可以保护初始矩阵的每个元素的位置和数目，达到了正确性、隐私性、可验证性和高效性的目的。本文的工作留下了一个有趣的问题，其他矩阵运算比如矩阵秩的计算、矩阵分解、矩阵的特征多项式以及特征值，对于资源有限的客户端来说，这些操作同样也是非常昂贵，因此也可以考虑外包给云服务器。基于其他矩阵运算，如何设计更高效、更安全的协议，是一个值得研究的课题。除此之外，在有限域上设计一个可验证的安全外包计算协议将是非常有意义的。