基于波动法的双层板振动功率流分析
2020-01-10杨培凯陈美霞陈乐佳
杨培凯,陈美霞*,陈乐佳
1 华中科技大学 船舶与海洋工程学院,湖北武汉430074
2 中国舰船研究设计中心,湖北武汉430064
0 引 言
耦合双层板结构常见于船体结构中,例如船底板、舱壁等,其弯曲振动和面内振动及辐射噪声与舰船的安全性和适用性密切相关。因此,研究双层板结构振动功率流有助于舰船减振降噪设计。
目前,国内外基于波动法的耦合结构振动功率流相关研究多为L 型板,而对双层板结构的功率流分析却不多见。 例如:Kessissoglou[1]运用波动法研究了L 型板的振动与功率流特性,结果表明,面内波在低频段对功率流的影响不大,但在高频段作用显著;Cuschieri 等[2-4]分析了薄板和厚板情况下的L 型板功率流,发现薄板的面内波在弯曲波波数与板厚的乘积小于0.1 时的作用可以忽略不计,大于1 时影响较大;Zhang 等[5]讨论了双层耦合板和“口”字型耦合板的振动特性,发现面内平均振幅远低于弯曲振动,仅在共振峰处的面内波幅值与弯曲波幅值接近;朱瑞仪[6]基于波动理论将板结构简化为梁的方法,分析了多转角结构和双层板结构的功率流及其振动衰减特性;赵芝梅等[7]基于波导方法讨论了激励特性对L 型板振动功率流的影响,重点分析了激励力角度和力矩混合等激励特性对面内波的影响;漆琼芳等[8-9]采用波动法研究了有限尺寸耦合板的振动功率流与板的激励力角度及连接角度的关系,结果表明,较低频率时的弯曲波功率流远大于面内波功率,而高频时二者相当;姚熊亮等[10]基于波动理论分析了典型船舶中振动波的传递特性,结果表明突变截面使阻抗失配,由此加剧了振动波的转换,使隔振效果得到改善;赵建学等[11]采用平均法导出了系统功率流传递率,发现双层隔振系统有比等效线性隔振系统更好的低频隔振性能。
鉴于目前使用波动法分析耦合板功率流的研究成果较多,而对于双层板结构的相关研究则较为少见,本文将基于薄板理论采用波动法建立有限尺寸双层板的振动模型,在结构耦合处断开,离散后将每块板的运动方程组装,求解得到振动响应。在此基础上,计算弯曲振动功率流和面内振动功率流,并分析激励力角度、连接件角度和厚度对振动功率流的影响,以为双层板结构的设计提供一定的理论指导。
1 理论推导
1.1 双层板运动方程
本文研究的耦合双层板结构由上、下2 层矩形薄板和中间连接板组成,并将双层板模型在激励力处及结构连接处断开后离散为6 个区域,记为板1~板6,图1 示出了6 个板各自的局部坐标方向和内力方向。图中:ui,vi,wi分别对应第i块板在xi,yi,zi方向的振动位移;θi=∂wi/∂xi,为转角;Vxxi,Mxxi,Nxxi和Nxyi分别为第i块板横截面上等效的法向纯剪力、弯矩、面内纵向力和面内剪切力,内力表达式见文献[1];简谐激励力F(x0,y0)与x轴夹角记为α(以下称激励角),板2与板4 的夹角记为β(以下称连接角);板宽为Ly,板1~板6 在y=0 和y=Ly处均为简支边界,板1 和板5 的左端及板3 和板6 的右端均为自由边界。
由Poisson-Kirchhoff 薄板假设[1],不考虑剪切变形情况下薄板的振动微分方程为

式中:D=Eh3[12(1-μ2)],为板的弯曲刚度,其中E,h,μ分别为杨氏模量、薄板的板厚、泊松比;4=∂4/∂x4+2∂4/∂x2∂y2+∂4/∂y4,为 算 子;ρ为 薄板的密度;cl,ct分别为纵波和剪切波波速;Fx,Fy和Fz分别为激励力在对应方向上的分量;t 为时间。

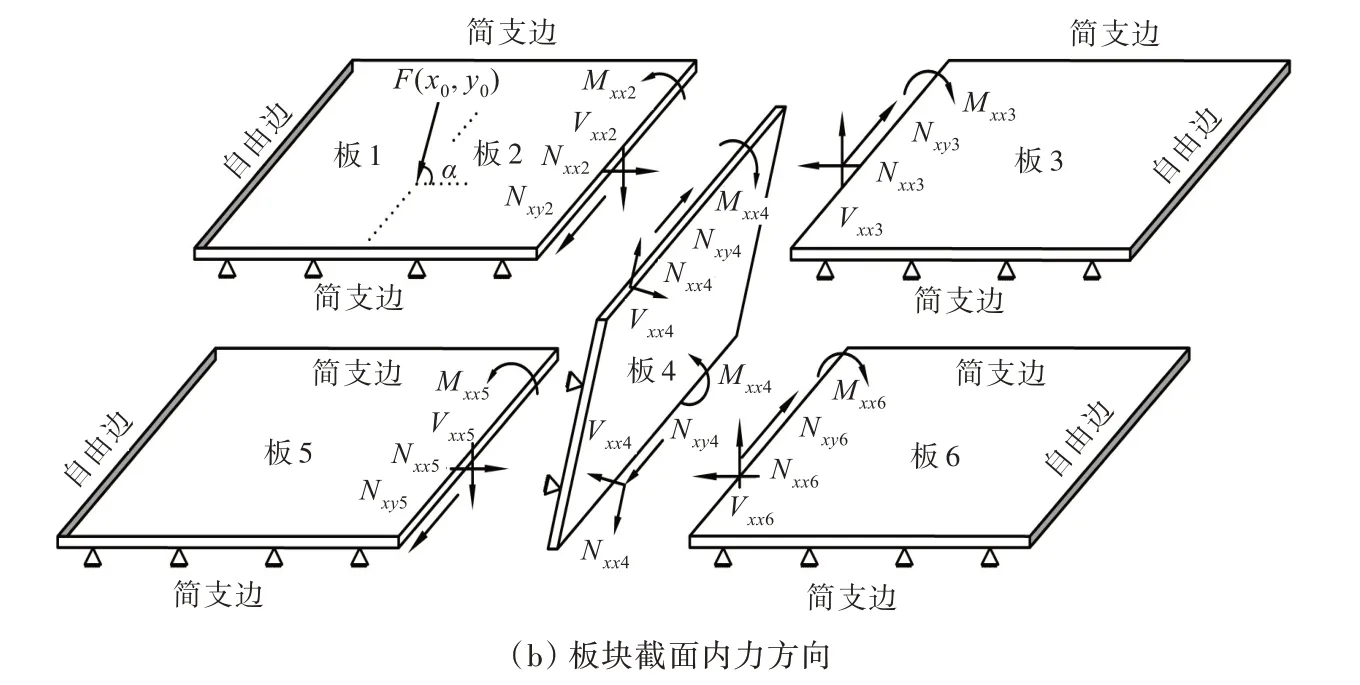
图1 双层板位移和内力示意图Fig.1 Schematic diagram of double-layer plate displacement and internal force
如图1 所示,离散后的双层板的6 个区域记为板1~板6,Lxi为各板沿局部坐标x轴方向的板长,i=1,2,3,4,5,6。由于板在y=0 和y=Ly处均为简支边界,故6 个区域内的振动位移响应(省略时间项)如式(2)所示。

式中:设Wi,m(xi)=Aiekxi,为第i 块板上面外方向的位移通解形式,其中,下标m 为模阶数,Ai为位移函数中的待定系数,回代到振动式(1)中可得模态波数k的4 个根;ky为板结构沿y方向的模态波数,ky=mπ/Ly,从而得到Wi,m(xi)的表达式。采用同样的方法,可得2 个面内方向的位移Ui,m(xi)和Vi,m(xi)的表达式,如式(3)所示。


1.2 边界条件和连续性条件
由1.1 节的推导可知,双层板离散后,板1~板6 共含48 个位移系数待求解。本文取双层板中的板1~板4 作为边界条件及连续性条件进行分析。
在x1=0 和x3=Lx1+Lx2+Lx3处为自由边界时,截面上的剪力、弯矩、面内纵向力和面内剪切力均为0,由向量表示如下:

在截面x1=x2=x0的位移和内力连续条件为:
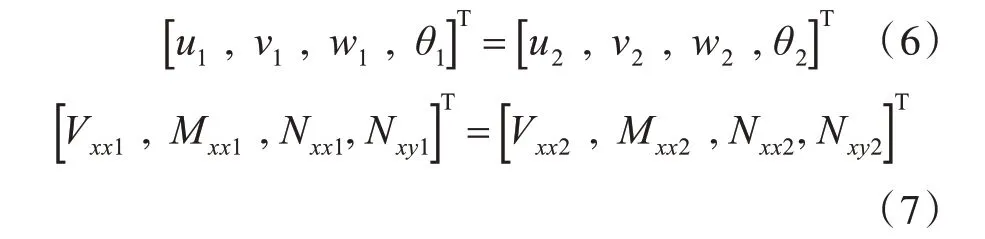
板2,板3 与 板4 连 接 处x2=x3=Lx1+Lx2,x4=0 位移和内力连续条件为:

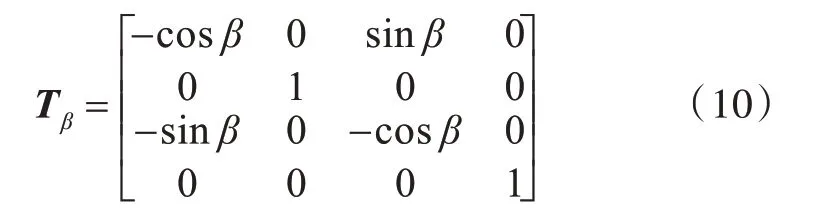
双层板板1,板2,板3 及板4 通过边界条件和连续条件可以得到式(4)~式(9)共28 个方程,板4,板5 和板6 采用同样方法也可列出其他剩余的20 个方程,这里不再赘述。
1.3 简谐激励力
如图2 所示,在板1,板2 连接线上的点(x0,y0)处,狄拉克函数δ表示的作用集中力F=F0δ(x-x0)δ(y-y0)(其中F0为振动幅值)时,可将其沿x,y,z 方向分解。本文重点讨论振动波沿x 方向的传递,即激励力垂直于y 轴,则α为激励力与x 轴的夹角,此时各方向的激励力分量为

此时,需对1.2 节的内力连续方程式(7)中的剪力和面内纵向力这2 项进行修正,则有
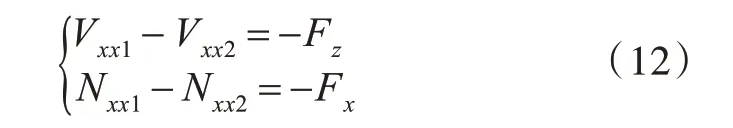

由修正后的激励力作用截面处的连续方程,结合1.2 节中板1~板6 的边界条件和连续条件,对所有板的运动方程进行组装,得到双层板的运动方程为

式中:A为48×48 的系数矩阵;向量X由各板位移函数中的48 个待定系数组成;F为作用力向量,并且仅有2 项不为0,即修正后的式(13)等号右侧2 项,再由X=A-1F可求解得到6 块板的48个未知系数,最后代入式(2)和式(3),可得各个板在简谐激励力作用下的振动响应。

图2 平板上的简谐激励力Fig.2 Simple harmonic excitation on the plate
1.4 振动功率流
1.3 节得到振动位移响应后,可由式(15)求得弯曲波功率流和面内波功率流。

式中:Pb为弯曲波功率流;Pin为面内波功率流;Re 为取实部。
弯曲波功率流和面内波功率流二者相加为总功率流,记第i块板在ω1~ω2频带内结构的振动功率流平均值Pi为

式中,Qxxi,Mxxi,Mxyi,Nxxi,Nxyi分别为第i 块板横截面上的剪应力、弯矩、扭矩、面内纵向力和面内剪切力,内力表达式参见文献[1]。
2 数值计算与分析
2.1 收敛性与有效性分析
应用模态叠加原理,需要足够大的模态截断数才可以保证收敛性。本文将有限元计算结果与解析法结果进行了对比,以验证结果的有效性。表1 所示为双层板尺寸及材料参数。
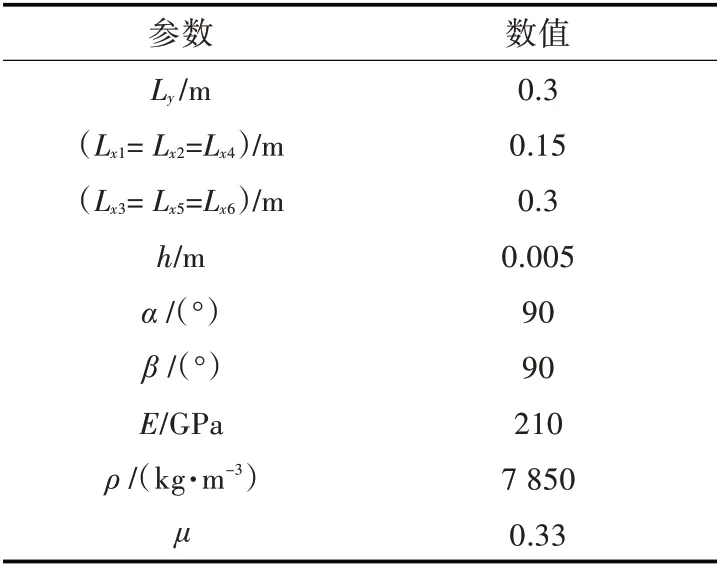
表1 物理参数及材料参数Table 1 Physical and material parameters
激励作用在板1 上的力位于点(x0,y0)=( 0.15,0.15) 处,振动幅值F0=1,如图1 所示。计算频段为1~5 kHz,分别取模态截断数M=6,10 和14,得到激励点(x0,y0)=( 0.15,0.15) 在各截断数下的横向位移w频响曲线,如图3(a)所示。数值算法则采用有限元软件ANSYS 求解,采用shell 63壳单元建模,共划分18 万个网格,取测点1 为板1上 的(x0,y0)=( 0.15,0.15) 处,测 点2 为 板6 上 的(x6,y6)=( 0.15,0.15 )处,然后与本文采用波动法,得到的横向位移振动响应结果进行对比,如图3(b)和图3(c)所示。
由图3(a)可见,在0~5 000 Hz 的计算频段内,模态截断数M 为10 和14 时的横向位移频响曲线计算结果已基本重合,取截断数M=14 已足以保证结果得到收敛。
由图3(b)和图3(c)可见,本文方法与有限元方法得到的横向位移振动响应结果基本吻合,这验证了本文方法的有效性和准确性。后续计算中,位移函数的截断数M 均取为15。

图3 横向位移响应波动法收敛性和有效性分析(基准位移10-12 m)Fig.3 Transverse displacement analysis of the convergence and effectiveness by wave method(ref.value 10-12 m)
2.2 不同角度激励下的振动功率流
本节采用了2.1 节相同的双层板模型参数。分析时,分别取激励角α=30°,60°,90°。设板2上x2=0.18 m 为激励板观测面,板6 上x6=0.48 m为接收板观测面,然后计算并分析上述2 个观测面处低频段和高频段下激励板及接收板的弯曲振动以及面内振动功率流,结果如图4~图7 所示。图中,平直虚线所示为α=90°时在相应频段内的功率流平均值。
由图4 可看出,在低频段内激励板的弯曲振动功率流远大于面内振动功率流,其平均值相差超过12 dB,且弯曲振动功率流随激励角α的增大而增大,面内波则相反。
由图5 可看出,在低频段内接收板同样满足了弯曲振动功率流远高于面内振动功率流的规律,其平均值相差30 dB,二者均随激励角的增大而增大,但相对于激励板而言,弯曲振动功率流和面内振动功率流的平均值都有较大衰减。
由图6 可看出,激励板中的弯曲振动功率流与面内振动功率流平均值相差仅3 dB,弯曲振动功率流随着激励角度的增大而增大,但面内振动功率流随之减小。

图4 低频段内激励板x2=0.18 m 处的振动功率流(基准功率流10-12 W)Fig.4 Excitation plate vibration power flow at x2=0.18 m in low frequency band(ref.power flow 10-12 W)

图5 低频段内接收板x6=0.48 m 处的振动功率流(基准功率流10-12 W)Fig.5 Receiving plate vibration power flow at x6=0.48 m in low frequency band(ref.power flow 10-12 W)

图6 高频段内激励板x2=0.18 m 处的振动功率流(基准功率流10-12 W)Fig.6 Excitation plate vibration power flow at x2=0.18 m in high frequency band(ref.power flow 10-12 W)

图7 高频段内接收板x6=0.48 m 处的振动功率流(基准功率流10-12 W)Fig.7 Receiving plate vibration power flow at x6=0.48 m in high frequency band(ref.power flow 10-12 W)
由图7 可看出,接收板中,随着频率的增加,面内波功率流也逐渐增大,这与弯曲波功率流相差无几。
通过对图4~图7 的分析,可以得到如下结果:
1)在低频段内,弯曲振动功率流远远大于面内振动功率流,但随着频率的增加,面内振动功率流逐步增大,与弯曲振动功率流相当。
2)在全频段内,弯曲振动功率流随着激励角度的增大而增大,但面内振动功率流在高频段内随激励角的变化规律与低频段相反,即随着激励角的增大而减小。
综上所述,面内振动功率流变化的原因源于2 个方面:一是激励直接引起的振动,二是弯曲和面内波的波形转换。一方面,激励角的增大导致了垂直于板的激励力分量增大,面内激励力分量减少,从而使面内的振动较小,而弯曲的振动较大;另一方面,尽管激励角的增大使激励板的面内振动相对较弱,但弯曲振动波也会经过波形转换更多地变为面内波。因此,计算得到的功率流是外部激励和内部波形转换共同作用的结果。当频率较低时,薄板纵向刚度远比弯曲刚度的大,故激励力在面内方向的分量引起的振动功率流数值较小;当激励角度增大时,面内力的分量会更小,而图4(b)~图7(b)显示其随着角度的增大,振动功率流也会增加,造成此现象的原因是在此阶段的波形转换效果明显,起到了主要作用;而频率较高时,纵向刚度和弯曲刚度大小相当,激励力的面内分量直接作用逐渐凸显,在此阶段,激励力直接作用带来的面内振动功率流作用更加明显。
2.3 连接件板4 对振动功率流的影响
本节采用与2.1 节相同的双层板模型参数。分析连接角β=30°,60°,90°时接收板6 上截面x6=0.48 m 处在0~1 000 Hz 频率范围的功率流,以及连接角β=90° 时板4 的厚度分别为5,7,9 mm 情况下板6 上截面x6=0.48 m 处观测到的功率流,结果如图8 和图9 所示。
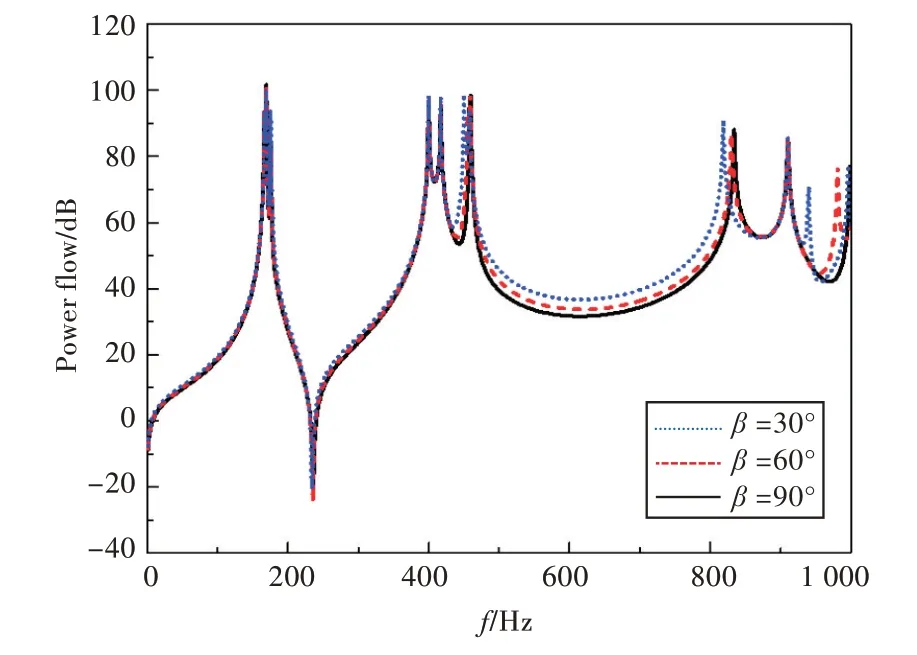
图8 不同连接角下接收板6 的振动功率流(基准功率流10-12 W)Fig.8 Vibration power flow of receiving plate-6 at different connection angles(ref.power flow 10-12 W)

图9 不同板厚下接收板6 的振动功率流(基准功率流10-12 W)Fig.9 Vibration power flow of receiving plate-6 at different plate thicknesses(ref.power flow 10-12 W)
由图8 可看出,总体上,总功率流随着连接角的增大而略有下降。连接角为90°时,减弱的作用表现得尤为明显,这是因为此时面板剪力方向平行于腹板的面内方向,弯曲波和面内波的波形转化效果明显,且波形转化随着频率的升高而加剧;振动传递过程中的能量衰减更明显,从而使接收板的功率流曲线也呈下降趋势[12]。
由图9 可看出,接收板的振动功率流受连接件的板厚影响较大,总体上,总功率流随着连接板厚度的增大而下降,且峰值频率也会右移。这是因为连接板厚度的增大使板的刚度增大,连接板的能量传递和波形转化作用都会提升,与之对应的功率流衰减也更多,从而导致接收板的功率流曲线呈下降趋势。
3 结 论
本文基于薄板理论与波动法,建立了有限尺寸双层板的耦合振动模型,并通过有限元对比验证了计算方法的准确性。在上述基础上,分析了不同激励角、连接角及其厚度对振动功率流的影响,并得到如下结论:
1)在低频段,激励板和接收板的弯曲波功率流远大于面内波功率流,随着频率的增大,二者逐渐靠近。
2)在低频段,激励板和接收板的面内振动功率流远小于弯曲波功率流,但在高频段二者相当,原因是二者主要受到外部激励力和波形转换这2个因素的影响;激励板和接收板均满足在低频段随着激励角的增大而增大的规律,此时二者主要受到波形转换的影响;在高频段,二者随着激励角的增大而减小,此时受激励力的直接影响较大。
3)接收板功率流的大小与双层板连接角及厚度密切相关,即连接角越是接近于垂直波形,其转化效果就越明显;同时,连接件的厚度越大,功率流的损耗也会增大,使得功率流曲线呈下降趋势。因此,在实际工程中,应在允许的范围内将双层板中的连接角设计为接近90°,并适当选择稍大的板厚以获得较好的减振效果。
