舰船进气格栅隐身性分析及灵敏度计算

2020-01-10杜晓佳丁凡

中国舰船研究 2019年6期

杜晓佳，丁凡

中国舰船研究设计中心，湖北武汉430064

0 引言

舰船隐身技术是通过减缩舰船各物理场特性，有效降低敌方探测器和制导武器威胁的一种技术，是舰船现代化水平的重要标志［1-3］。舰船进气格栅是船体外部进气道进口安装的金属格栅结构，可防止异物进入进气管路，对进气管道空气流体特性产生影响，若其设计达不到标准，会影响舰船动力系统的正常运行。以燃气轮机为动力的水面舰船，受进气需求的影响，外露的进气格栅数量多、面积大，其格栅雷达散射截面（RCS）的大小将影响舰船的整体隐身水平。开展船舶进气格栅隐身性与气动特性的设计与综合优化，并使之具有良好的气动性能与隐身性能，可提升水面舰船整体技术水平。

目前，在航空领域对进气格栅的气动特性与隐身性综合优化的研究较多，而在船舶领域的研究较少。国内外学者在飞机进气格栅电磁散射特性方面做了大量的仿真研究和实验论证。桑建华［4］对格栅进行了阐述，并给出了格栅RCS 测试的初步结果；张乐［5］的研究结果显示，在飞机格栅设计过程中，气动特性与隐身性之间往往是相矛盾的。

隐身性分析是开展进气格栅气动特性与隐身性综合优化的前提之一。考虑到进气格栅的几何设计参数众多，对所有参数进行隐身性优化计算的成本过高。本文将以某典型船用进气格栅设计方案为研究对象，开展进气格栅参数化建模及电磁散射计算参数设定；根据进气格栅的物理特征，选取合适的电磁散射计算方法，获取不同参数下格栅模型雷达波散射计算的结果；通过开展散射特性分析及灵敏度计算，获取进气格栅在雷达波隐身性能优化中的主要几何参数顺序。

1 进气格栅隐身性评估模型建立

1.1 进气格栅参数化电磁模型

几何参数化建模是开展进气格栅的气动特性与隐身性能综合优化的基础。基于ANSYS 软件的APDL 语言进行参数化的进气格栅几何建模，如图1 所示。在参数化建模过程中，对进气格栅几何基本元素进行了分析和定义，参数具体定义及设定值如表1 和图2 所示，设定船体舷侧壁板倾斜角度为7°。假定进气格栅和船体结构材质均为理想金属。完成格栅几何模型参数化建模后，采用三角形面元进行网格划分，网格最大尺寸按照1/8 电磁波长进行剖分。

1.2 雷达隐身性计算参数及评价设定

图1 进气格栅几何模型Fig.1 Geometric model of air-intake grille

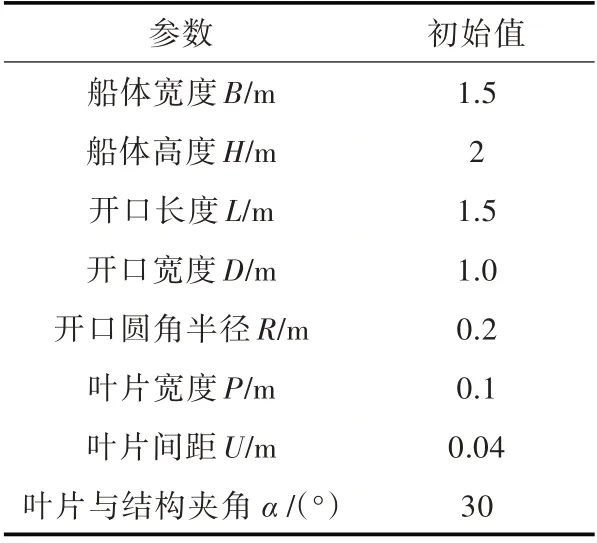
表1 进气格栅几何参数及初始值Table 1 Geometric parameters and initial values of air-intake grille

图2 进气格栅几何参数定义Fig.2 Definition of geometric parameters of air-intake grille

水面舰船隐身设计主要考虑掠入射条件下的预警机及反舰导弹的探测威胁，因此本文的进气格栅RCS 评估研究仅针对沿水平威胁的雷达波展开。舰船进气格栅的RCS 计算坐标系如图3 所示，其中φ为照射的水平方位角。考虑格栅厚度影响，在进行雷达波隐身评估时，格栅背面为进气道，仅考虑前向的威胁，方位角φ的考评范围设定为-85°～85°。为更好地体现RCS 的变化规律，本文中所有的计算曲线均做3°平滑处理，假定入射波为10 GHz 垂直极化雷达波。

图3 进气格栅计算坐标系Fig.3 Coordinate system of air-intake grille

目前舰船RCS（用变量σ表示）评估最常用的标准为目标在威胁区域内RCS 的平均值，用表示，即

此外，为了更为直观表征格栅的隐身效果，文献［4］中提出了格栅电磁屏蔽效率η的概念，其定义公式为

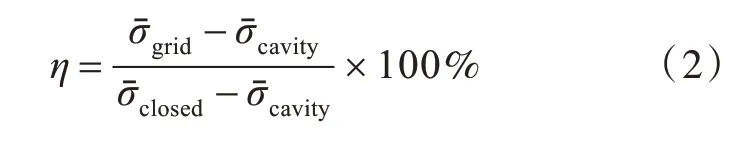
式中：为格栅模型RCS 平均值；为进口开放模型RCS 平均值；为进口封闭模型RCS平均值。

2 进气格栅电磁散射计算方法分析

舰船类目标散射主要由镜面反射、腔体散射、耦合散射、边缘散射等组成。在进行水面舰船雷达散射截面计算时，通常采用高频近似方法或快速多极子算法（FMM）进行求解，其中常用的高频近似方法有物理光学法（PO）、射线追踪法（SBR）和等效边缘电流法（EEC）等。

2.1 物理光学法

物理光学法遵循高频场的局部性原理，忽略了各点感应电流间的相互影响，并假定散射体阴影区内的电磁场场值为零。对于理想导体，物理光学法获取的RCS 平方根的物理光学表达式为

式中：er为接收装置电极化方向的单位矢量；h为磁场极化方向的单位矢量；S为散射方向的单位矢量；v为电磁波入射方向的单位矢量；n为散射体表面的外法线单位矢量；k为波数；S0为照明区；r为照明区中的网格点s 到观察点P 的距离。物理光学法不能计算由于目标表面不连续产生的电磁散射，不能预估绕射的影响。

2.2 射线追踪法

射线追踪法基于几何光学原理，将入射的均匀平面波划分为密集的射线管，高频电磁波的能量沿着细长射线管传播，每个射线管在腔体内经多次反射，最终返回口径处。射线追踪法需要根据目标对划分的射线进行合理的模型选择，否则很难达到要求的精度。

2.3 快速多极子方法

快速多极子方法的基本原理是：将目标表面离散得到的子目标分组，自身组和相邻组采用直接矩量法计算，非相邻组采用聚合－转移－配置方法计算。所有源散射体i 对场散射体j的贡献用快速多极子方法表达为［5］

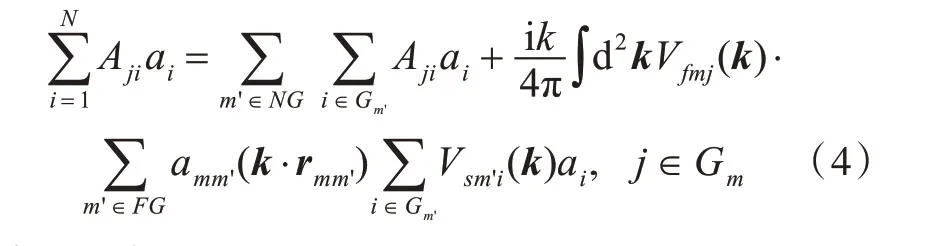
式中：ai为第i个源散射体的电流幅度；NG 为附近组的贡献；FG 为非附近组的贡献；amm'为转移因子；Vsm'i为聚合因子；Vfmj为配置因子；k为电磁波传播方向矢量；rmm'为m到m′的距离矢量；Gm和Gm′分别为以m和m′为中心的组；m′为最底层组中心；Aji为待求电流密度；d 为求导。理论上快速多极子方法是严格的，且精度可控；它既加快了积分方程的求解速度，也能够保持矩量法的计算精度。

进气格栅作为一种复杂的多重散射体，整体尺寸远大于入射雷达波波长，但叶片尺寸相对于入射雷达波长并不处于高频光学区。此外，进气格栅的叶片数量较多，耦合散射和边缘散射不容忽略。在上述方法中，快速多极子方法最适用于进气格栅RCS 仿真计算，能够获取较高的计算精度和计算效率。

3 进气格栅雷达波反射特性分析

3.1 船体结构与格栅耦合散射分析

根据表1 中的几何参数初始值，建立如图4 所示4 种模型：船体结构无格栅模型（model-1）、船体结构+腔体模型（model-2）、船体结构+格栅模型（model-3）和格栅无船体结构模型（model-4）。按照1.2 节假设条件，完成这4 种模型的RCS 仿真计算，结果如图5 所示。

对比model-1、model-2 与model-3 的RCS 值(σ) 分布曲线，船体结构在无格栅情况下（model-1），雷达波隐身性能最佳，主要由于此时雷达波反射仅存在镜面散射效应；船体结构+腔体模型（model-2）隐身性最差，各方位角下的RCS 值均大于船体结构+格栅模型（model-3），可以看出格栅能够显著降低进气口的腔体反射；格栅法向峰值区域，即0°～5°范围内，船体结构+格栅模型（model-3）的RCS 分布小于船体结构无格栅模型（model-1），可见格栅的存在一定程度上降低了格栅法向峰值区的峰值；在5°～80°范围内，由于进气格栅的存在，导致船体结构+格栅模型（model-3）相对船体结构无格栅模型RCS 均有明显上升。由此可见：进气道产生的腔体散射极大，当布设格栅后，可明显降低进气道腔体反射效应，进气格栅能够降低船体外板法向的RCS，但会在其他角度域形成雷达波反射。

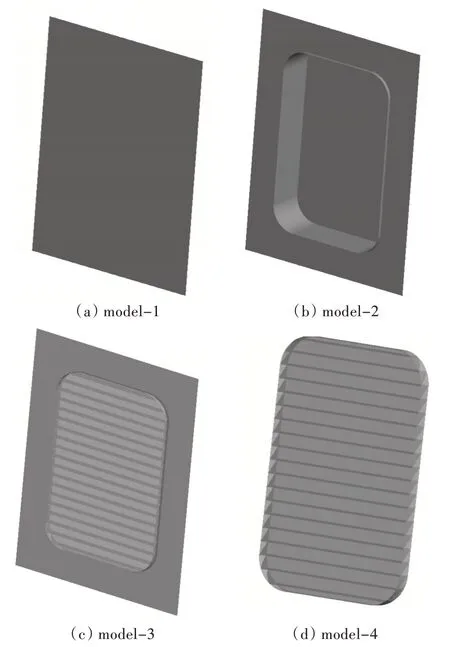
图4 船体结构与格栅耦合分析模型Fig.4 Coupling analysis models of hull structure and grille

对比model-1，model-3 和model-4 的RCS 分布可知，在无船体结构情况下，格栅的RCS 分布变化主要分布在0°～25°范围内；在其他角域，由于船体自身的RCS 远小于格栅，故船体结构的存在对格栅RCS 影响不大。

3.2 格栅开口几何参数的影响

格栅开口几何参数有开口长度L、开口宽度D及开口圆角半径R。针对L分别为1.4，1.5及1.6 m、D 和R 不变情况下的3 种规格进气格栅模型进行RCS 仿真计算（图6）。由图6 可见，L 对格栅法向0°的RCS 峰值有明显影响，在32°左右的RCS 峰值也随着L 的变化而发生改变。

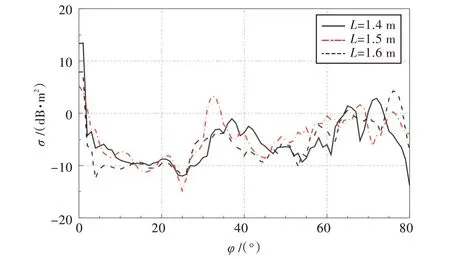
图6 开口长度L 对σ 的影响Fig.6 Effect of grille length L on σ

针对D 分别为0.9，1.0 及1.1 m、L 和R 不变的情况下的3 种规格进气格栅模型进行RCS 仿真计算（图7）。由图7 可见，D 对格栅RCS 分布的影响相对较小。

图7 开口宽度D 对σ 的影响Fig.7 Effect of grille width D on σ

针对R 分别为0.15，0.20 及0.25 m 的3 种规格进气格栅模型进行RCS 仿真计算（图8）。由图8可见，R 对进气格栅的RCS 分布产生一定的影响，导致0°和32°处的RCS 峰值均有所变化。

图8 开口圆角半径R 对σ 的影响Fig.8 Effect of grille fillet radius R on σ

表2 为不同格栅开口参数下的RCS 平均值和电磁屏蔽效率计算结果。可以看出，D 和R 对RCS平均值和格栅屏蔽效率几乎没有影响；由于L 对格栅法向0°和32°左右的RCS 峰值的影响，其对格栅屏蔽效率的影响相对较大。

表2 不同格栅开口几何参数下的RCS 统计结果Table 2 RCS statistical results under different geometric parameters of grille

3.3 叶片几何参数对RCS 的影响

针对叶片宽度P、叶片间距U 及叶片与结构夹角α这3 个叶片几何参数，分别对不同叶片参数下的进气格栅模型进行电磁仿真计算，结果分别如图9～图11 所示。

由图9 可见，P 对格栅RCS 的影响较为集中，即在26°左右的RCS 波谷有明显变化。由图10 可见，U 对格栅在32°处的RCS 峰值位置产生较大影响，格栅法向0°附近的RCS 峰值也有明显变化。由图11 可见，α也会对进气格栅在32°左右的RCS 峰值位置产生影响。

图9 叶片宽度P 对RCS 的影响Fig.9 Effect of blade width P on RCS

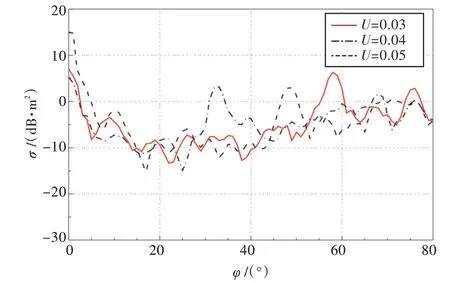
图10 叶片间距U 对RCS 的影响Fig.10 Effect of blade distance U on RCS

不同叶片几何参数下的RCS 统计结果如表3所示，叶片宽度P 和叶片结构夹角α对格栅RCS在20°～60°威胁区域分布的影响较大，但对和电磁屏蔽效率影响较小。相比而言，叶片间距U 对和屏蔽效率的影响相对较大。

3.4 叶片方向及后部遮挡物的影响

船用进气格栅叶片分布方向有横向和纵向两种，分别建立了在等参数下的横向和纵向分布的进气格栅模型（图12）。这2 个进气格栅开口尺寸和叶面大小等几何参数均相同，只有格栅的分布不同，分别对2 个模型开展电磁散射特性计算，结果如图13 所示。

从图13 中可以看出，横向格栅的RCS 分布普遍要比纵向格栅要高，尤其是±33°左右有2 个波峰。对比-80°～0°区域与0°～80°区域，纵向格栅的RCS 分布的差异主要体现在-22°和68°处的峰值。

图12 横向和纵向进气格栅模型Fig.12 Models of transverse and longitudinal air-intake grille

图13 格栅叶片方向对RCS 的影响Fig.13 Effect of blade direction on RCS

为防止小型异物进入进气道，进气格栅后部一般设有金属网丝。考虑到金属网丝几何尺寸较小，而整体尺度较大，电磁散射模型建模极为困难。因此，本文采用极端模拟对比，将金属网丝间隔视为无限小，即对进气格栅后面全部采用金属遮挡，横向和纵向进气格栅模型后部遮挡模型如图14所示。对采用后部遮挡的横向和纵向分布的进气格栅模型展开计算，结果如图15和图16所示。

由图15 可见，受后部遮挡的影响，在整个角域内，横向进气格栅的RCS 增大，RCS 峰值的数量和幅值均有所增强，后部遮挡会对横向格栅的雷达波隐身性产生较大影响。

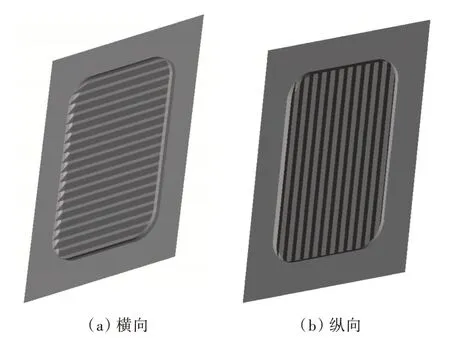
图14 进气格栅后部遮挡模型Fig.14 Back cover model of air-intake grille

图15 横向进气格栅后部遮挡对RCS 的影响Fig.15 Effect of back cover on RCS of transverse grille

图16 纵向进气格栅后部遮挡对RCS 的影响Fig.16 Effect of back cover on RCS of longitudinal grille

由图16 可见，纵向进气格栅在-80°～0°范围内受叶面遮挡的影响，格栅后部有、无遮挡物对纵向进气格栅的影响较小，其峰值量级和分布变化不大。在0°～80°角域范围内，后部金属遮挡处于可视范围内，此区域的RCS 峰值量级和分布出现较大变化，尤其是20°～70°范围内出现多个较大峰值。

在横向和纵向进气格栅有、无后部遮挡情况下，RCS 平均值和电磁屏蔽效率统计结果如表4所示。由表可见，受多次反射的影响，后部遮挡会显著增加进气格栅的雷达波散射，从而降低了对横向格栅的电磁屏蔽效率。而对于纵向格栅，后部遮挡对RCS 平均值和电磁屏蔽效率影响相对较小，且一定程度上还提高了纵向格栅的电磁屏蔽效率。

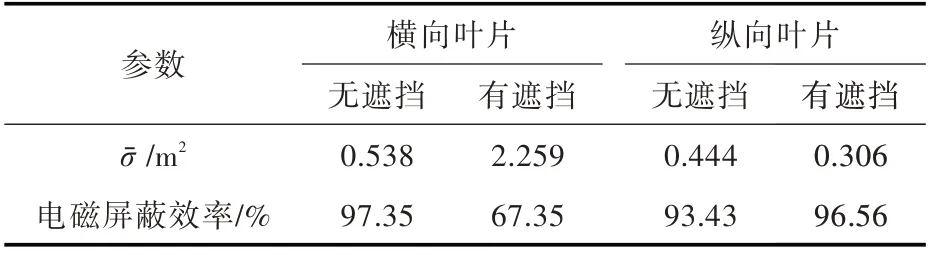
表4 不同叶片方向及遮挡的格栅RCS 统计结果Table 4 RCS statistical results with different blade direction and back cover of grille

4 进气格栅几何参数灵敏度分析

4.1 RCS 灵敏度计算方法

灵敏度分析研究模型输出y的变异与各个输入参数xi的变异之间如何分解［6-7］。考虑到组成进气格栅的几何参数众多，难以对所有参数进行优化使其性能最优，需要计算雷达波隐身性能对进气格栅几何参数的灵敏度。通过进气格栅几何参数灵敏度计算分析，可以量化输入参数影响模型输出变异的重要程度，并找到关键参数，为开展进气格栅雷达波隐身性能优化提供方向。本文采用中心有限差分方法来近似计算格栅RCS 评估参数y对格栅各几何参数变量xi的导数［8-10］：