高雷诺数下水翼涡发放频率预报方法

2020-01-10侯磊丁云峰王晴宗智孙雷姜宜辰

中国舰船研究 2019年6期

关键词：雷诺数攻角流速

侯磊，丁云峰，王晴，宗智，孙雷，姜宜辰*

1 海军装备部驻武汉地区第二军事代表室，湖北武汉430064

2 大连理工大学船舶工程学院，辽宁大连116024

3 中国舰船研究设计中心，湖北武汉430064

4 船舶振动噪声重点实验室，湖北武汉430064

0 引言

涡激振动（VIV）被视为流体力学、结构力学、计算流体力学和声学等不同领域的重点问题。这些领域中关于VIV 的研究可见于Rockwell［1］，Williamson 和Govardhan［2］，Sarpkaya［3］，Bearman［4］和Assi 等［5］的综述中。流体与结构物相互作用会增加结构的振动，在特定工况下会造成结构破坏。此外，如果泄涡频率与结构的某一阶固有频率相等，共振会显著增加结构的振幅，结构的振动位移会俘获流体激励，造成所谓的“锁定”现象。Ausoni 等［6］在研究二维钝体水翼时发现，如果结构运动位于共振区间之外，泄涡频率遵循斯特劳哈尔定律，即“脱离锁定”。在锁定状态下，弯曲的涡量线变成平行于尾端的直线，涡强也会增大［7］。因此，研究水翼的绕流特性及涡发放机理，并以此为基础，对水翼泄涡流致振动进行探究是十分必要的。

Blake 和Gershfeld［8］在20 世纪80 年代全面回顾了前人关于水翼的研究工作。这些试验说明尾涡泄放在对称翼尾和钝体翼尾同时存在。Huerre与Monkewitz［9］和Oertel［10］分别给出了流动不稳定性和钝体尾流的概述。Lotfy 和Rockwell［11］做了钝体振动翼尾尾涡泄放研究，为之后的泄涡研究提供了参考。然而，钝体涡发放的研究结果并不能直接转换到流线型体，因为相比于钝体，流线型体首部和尾部的较大距离抑制了窄涡波动和首部停滞点之间的相互作用。

Ohmi 等［12］对机翼在大攻角下作强迫旋转和平移振动时涡的形成进行了深入的试验探究。Morikawa 和Grönig［13］则研究了此时旋涡的生成及其结构。Huang 等［14］对NACA 0012 翼型进行了试验分析，并探讨了翼根连接处与翼梢对涡激振动的影响。Jung 等［15］通过试验对低雷诺数下机翼绕流形成的涡街进行分析，发现机翼振动情况下的脱涡频率相对于机翼静止不动时要小。Davidson实验室针对水翼做了大量的试验研究，主要集中在两自由度理想翼型方面，观察测量水翼在水洞试验中的振动、空泡、压力分布等。Chae 等［16-17］对两自由度下的二维水翼进行了系统的研究，探讨了附连水质量、水动力阻尼、非线性流固耦合响应等对水翼稳定性的影响。

利用离散涡方法进行水翼涡发放频率特性的研究，在国内外并不多见。现有的研究大部分基于传统的经验模型或数值方法。经验模型，如尾流振子模型，只能用来求解结构的涡激振动响应，无法对尾流场的特征进行分析，且求解结果仅在数量级上接近真实值；而传统的数值方法，如有限体积、有限差分、有限元、大涡模拟和直接数值模拟等计算方法和模型在求解VIV 时需要巨量网格，难以获得足够高的计算效率和精度［18-19］。

离散涡方法是拉格朗日体系下的一种涡动力学算法，该方法由集中涡模型发展而来，其基本思想是在物体表面直接产生离散涡元，涡元在流场中有限的区域内通过相互作用来模拟涡量场，对涡量场进行积分可以得到速度场，进而可以得到整个流场结构。该方法不依赖于流场网格，在涡量集中区涡尺度分辨率高，算法简单，程序易于并行化处理，可以选用大时间步长，由于整个求解过程中无需计算全部流场信息，相对于传统网格法，其计算量大大降低，极为适合高雷诺数情况下结构绕流和涡激振动问题的求解［20-22］。按照离散的涡元基本形状，离散涡（DVM）可以分为点涡法、涡片法、涡丝法、涡杆法、涡团法和混合方法等；根据初始新生涡强度确定方式的不同，可以分为面元法和涡量—流函数法；根据粘性的处理方式，可以分为面积扩散涡方法、随机涡方法和确定性涡方法等；根据涡元诱导方式，可以分为直接法、格子涡法和快速多极子展开法；根据边界处理方式，可以分为镜像涡法、涡元法、容量矩阵法等［23-26］。

本文将以二维NACA 66 系列水翼为例，首先通过与试验数据对比，验证离散涡方法对于模拟高雷诺数下涡发放频率预报的适用性和准确性。然后，应用此方法，模拟不同流速下NACA 66（MOD）水翼的涡发放情况，并分析流速对水翼泄涡频率的改变情况。最后，在某一相同高雷诺数下，简要探讨水翼攻角对涡发放频率的影响规律，以便为分析螺旋桨叶剖面涡发放频率特性打下坚实基础。

1 基本原理

假设流体非理想不可压，由动量守恒和质量守恒组成的控制方程可写为：

式中：U为流体速度；t 为时间；f 为流体体积力；p为压力；ρ为流体密度；ν为流体运动粘性系数。对于重力场f=(0，0，-g)，方程两边同时取旋度，由于∇×f=0，∇×(∇p)=0，应用涡量—速度关系式ω=∇×U，可得

式（3）又称为旋涡扩散方程或涡量输运公式。从中可看出，对于非理想不可压流体，对流项与粘性扩散项之和控制涡量的变化。当流动为二维平面情况时，存在关系式：

将式（6）代入涡量—速度关系式，得到如式（7）所示的控制方程：

但上述方程难以直接求解，根据Chorin［27］所提出算子分裂的思想，动力学控制方程可以分裂为：

1）对流项

2）粘性扩散项

假设流场为无限域，只需要考虑物面边界条件和远场边界条件，其中物面条件为法向不可穿透和切向无滑移条件：

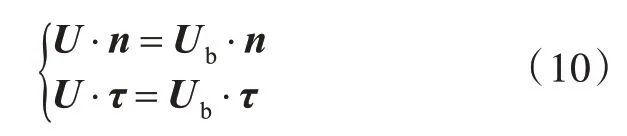
式中：n和τ分别为物面单位法向量和切向量；U为靠近物面处流体粒子速度矢量；Ub为物体速度矢量。在粘性涡中，只要满足无滑移和不可穿透条件中的任意一个即可，因为粘性涡的这两个条件是等价的［28］。将涡元布置在物面，点涡由物面产生脱落，并向外运动扩展，即可使物面不可穿透条件自动得到满足。物面点涡由于涡元间的诱导产生诱导速度，诱导速度和滑移速度相互抵消，从而满足无滑移条件。

在无穷远处满足无穷远速度条件：

根据Biot-Savart 定理，涡元对无穷远处的诱导速度为0，于是无穷远处的流体速度只有来流速度，所以远场的边界条件同样自动满足。

根据Chorin［27］提出的涡团速度分布公式：

式中：r 为诱导点位置与涡团中心位置的距离；θ为两点的相位角；σ为涡团半径；Γ为涡团的涡强，其由流函数方程确定；u 为诱导点切向速度，逆时针为正。将诱导速度代入式（6），并转化为直角坐标形式，则流函数可表示为

由于粘性作用，流场内的旋涡表现出一定的聚集性，只在流场有限区域内产生相互作用。离散涡方法基于涡量场这一特征，把从物体表面脱落，发展形成的连续旋涡场离散成一系列的涡元，通过模拟涡量场，得到速度场，进而获得整个流场结构［29-30］。根据这一思想，涡量场内任一点r 处的涡量为：

式中：Γi为位于ri处涡元的涡强；n 为当前流场内涡元总数；δ(r-ri)为狄拉克函数。如果认为流场是无限流场，求解式（8）对流项中的泊松方程可得到涡元诱导速度：

从式（15）可看出，涡元运动速度包括涡元之间的相互诱导部分和来流速度，而相互诱导项就是Biot-Savart定理。

计算出涡元t时刻速度U（r，t）后，经过时间步长dt，新时刻的位置矢量可以表示为

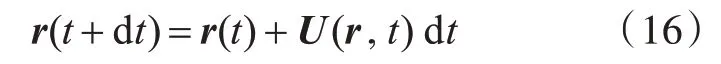
应该注意的是，上式并未考虑由于流体粘性而产生的位移，对于粘性扩散部分，类似热扩散方程，其基本解是格林函数：

式（17）与均值为0、标准差为s的正态分布的概率密度函数的形式相似：

式中：P 为概率密度函数；η为随机变量。这样，Δt时间步内涡元的随机扩散位移为

对于灰色定权聚类分析方法而言，白化权函数的表达式通常由相关行业的专家给定，决策权ηj的值可通过专家法进行确定，也可通过下述方法确定：

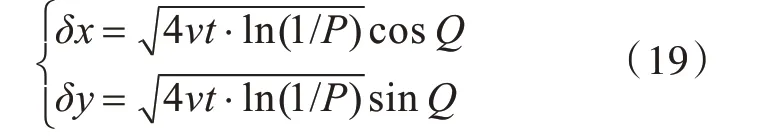
式中：P，Q两个独立随机变量满足P∈（0，1）和Q∈（0，2 π）。于是t+dt 时刻的涡元位置矢量可以表示为

式中，δr=(δx，δy)。

本文采用的随机涡方法需要将结构表面离散成节点，同时需要确定适用于该数值模型的新生涡生成位置及数目。首先，将物体看作一个np边形，其中np为边界单元数，单元端点为xi（i=1，2，…，n）。配置点xc，i，即满足速度边界条件的点。通常有两种布置方式：一种是将其与相应的外法向量ni布置在单元中点（如图1（a）所示），并假设物面上的新生涡强Γi集中在配置点上；另一种是将离散的涡元布置在流域内人工设置的边界层上，即沿端点外法向，距离端点一定距离，这个距离就是当地边界层厚度d（如图1（b）所示），涡强同样集中在配置点。

图1 配置点布置方式Fig.1 Configuration of discrete nodes arrangement

以圆柱为例探究两种布置方式对于本文使用的离散涡模型的适用性。一直径为D=0.2 m 的固定圆柱在遭遇速度为1.0 m/s 的均匀来流时，其新生涡强分布的表达式为

式中，θ为圆柱表面离散节点径向与流向的夹角。利用上述两种布置方式对该圆柱绕流问题进行模拟，离散节点数均为n，第2 种布置方式中人工边界层厚度d 根据经验设置为D/n。两种方式得到的新生涡强如图2 所示。

由图中对比可知，在物面离散节点数相同时，设置人工边界层的配置点布置方式得到的新生涡强更接近理论解，因此，在本文的水翼涡发放模拟中，采用第2 种布置方式。

图2 两种配置点布置方式新生涡强对比Fig.2 Comparison of new vortex strength between two node arrangements

此外，传统的CFD 方法通常利用网格对结构或流场进行划分求解，模拟的结果很大程度上取决于网格划分的合理性。本文采用的离散涡方法虽为无网格方法，但新生涡的数量同样会影响计算精度和效率。因此，选取上述固定圆柱进行讨论，同样根据新生涡强的数值对比来衡量最佳新生涡数目。令圆柱直径D 为0.2 m，流速为1.0 m/s，选取不同数量（n=40，80，120，160，200）的新生涡数，采用第2 种布置方式对该圆柱绕流问题进行模拟，并将新生涡强的结果与理论值进行对比。

图3 不同新生涡数目求解新生涡强理论值误差对比Fig.3 Tolerance comparison on vortex strength using various numbers of new-generated vortices

2 算法验证

2.1 算例模型

采用与Leroux 等［31］试验相同的NACA 66 水翼模型，弦长C=0.15 m，最大厚度为弦长的12%，最大厚度位于距离前缘45%弦长处。最大拱度为2°，位于弦长中心。试验中，水翼的宽度为0.191 m，水翼由不锈钢制作。NACA 66 水翼截面型式如图4 所示。

图4 NACA 66 系列水翼截面（最大厚度为弦长的12%，位于x/C=-0.05）Fig.4 Section of NACA 66 series hydrofoil（maximum thickness is 12% of chord length at x/C=-0.05）

2.2 刚性水翼涡发放

采用离散涡法对上述NACA 66 水翼在稳流下的涡发放进行模拟。设置NACA 66 水翼为刚体，攻角保持6°不变，模拟了4 种不同流速情况，对应的雷诺数分别为0.8×106，1.0×106，1.2×106和1.5×106。模拟的总时间长度为30 个周期，其中每个周期T为流体流过一个弦长所需时间（即T=C/U）。

图5 给出了雷诺数为1.0×106情况下水翼垂向载荷Fy在30 个周期内的变化历程。由图可见，垂向载荷时间历程中存在两种不同频率的震荡，其中周期约为0.5T 的高频振荡应是由涡发放直接引发，而周期约为10T 的振荡则是由涡团之间的相互影响产生。

图5 垂向载荷时间历程（Re=1.0×106）Fig.5 Time history of vertical load（Re=1.0×106）

2.3 涡发放频率对比

由于泄涡诱发水翼的垂向载荷发生波动，因此，能量谱中的最大谱峰所对应的频率等同于涡发放的频率。对垂向载荷进行傅里叶变换，为了达到精度和计算时间上的平衡，时间步长选为0.05T，经过傅里叶变换后，得到涡发放频率区间如图6 所示，其中包括预报值上限和预报值下限，两者的平均值视为涡发放频率的数值模拟近似值。

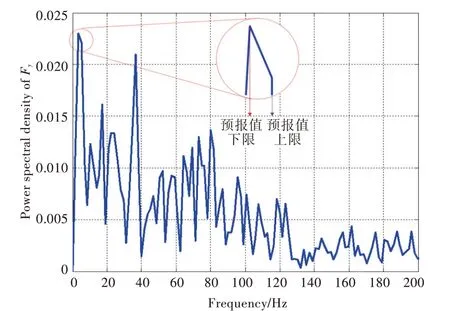
图6 垂向载荷能量谱（Re=0.8×106）Fig.6 Power spectral density of Fy（Re=0.8×106）

图6～图9 给出了NACA 66 水翼在4 种不同流速下的垂向载荷的能量谱，涡发放频率值见表1。将所得频率值与Leroux 等［31］发表的试验测量结果进行对比，可见在4 种流速下，测量值均落于预报的下限和上限范围内。图10 给出了数值模拟和试验测量的涡发放频率对比。由图中可以看出，离散涡法预报的频率平均值与测量结果吻合良好，且在较高雷诺数下，模拟结果更为准确，在低雷诺数时，预报值略高于试验结果。这可能是由于低雷诺数时水翼绕流边界层处于层流向湍流的过渡阶段，本文的数值模型未建立湍流模型，对边界层发展和分离采用随机走步进行近似处理，无法实现层流到湍流这一过渡状态的精确捕捉。

图7 垂向载荷能量谱（Re=1.0×106）Fig.7 Power spectral density of Fy（Re=1.0×106）

图8 垂向载荷能量谱（Re=1.2×106）Fig.8 Power spectral density of Fy（Re=1.2×106）

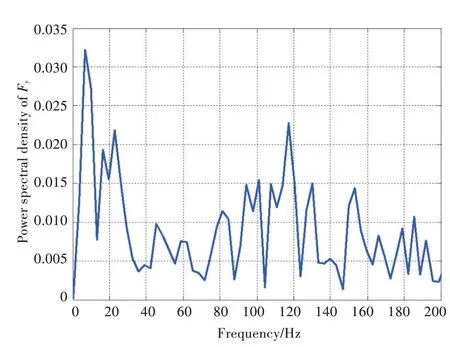
图9 垂向载荷能量谱（Re=1.5×106）Fig.9 Power spectral density of Fy（Re=1.5×106）

图10 涡发放谱峰频率试验与数值模拟对比Fig.10 Vortex shedding peak frequency（experiment&numerical simulation）

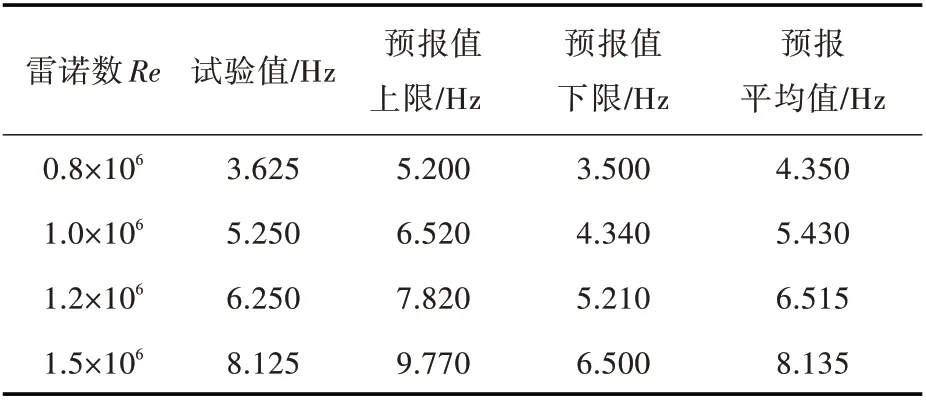
表1 涡发放谱峰频率对比Table 1 Comparison of vortex shedding peak frequency

通过实测数据与数值模拟数据，均可看出泄涡的频率随着雷诺数的增加而增加。为进一步分析流速对涡发放频率的影响，图11 对比了3 种流速下在t/T = 30 时刻的涡点分布图，其中蓝色虚线代表Re=1.5×106时的涡发放位置。对比可见，在水翼后缘1.5 个弦长内，Re=1.5×106时释放的涡对最多，其次为Re=1.2×106时，再次为Re=0.8×106时，这表明流速的增加会加快泄涡的频率。

图11 t/T=30 时刻NACA 66 水翼涡发放频率对比Fig.11 Vortex shedding frequency of NACA 66 series hydrofoil at t/T=30

3 流速与攻角对水翼涡发放频率的影响

螺旋桨是舰船三大噪声源之一，对其进行噪声预报是舰船声学设计过程中的一个重要环节。国内外学者开展了大量相关研究，Seol等［32-33］采用面元法得到螺旋桨的流场信息并将其代入声类比方程中，从理论上求解了流场任一点的辐射噪声。在数值模拟方面，Pantle 等［34］测量了自制螺旋桨在空气中工作时的噪声数据，之后对该桨噪声进行计算，发现计算结果在叶频和倍叶频上与试验数据吻合较好，从而验证了数值方法的可行性。然而，由于螺旋桨在水下工作时运动复杂，现有的测量和试验技术无法准确捕捉噪声信号，尤其是缺乏对于较高流速（如雷诺数Re ＞107），以及有初始攻角情况下螺旋桨不同叶剖面处涡发放频率及螺旋桨整体噪声的试验及数值预报研究。

无论采用理论方法还是数值模拟方法预报螺旋桨流噪声，都要先求解螺旋桨的湍流脉动，而在数值模拟方法中，湍流脉动的准确性又取决于湍流模拟方法。鲁利等［35］以DTMB 4119 螺旋桨为对象，采用雷诺平均N-S 方程、分离涡模拟法（DES）和大涡模拟法（LES）这3 种湍流模拟方法计算湍流脉动，并通过声学边界元预报螺旋桨流噪声，结果发现这3 种湍流模拟方法在一阶叶频处的预报结果相差不大，随着阶数的升高，采用LES 方法预报的结果与理论方法的结果吻合更好。然而LES 方法对网格要求高、计算量较大、计算效率偏低。本文采用的离散涡数值方法摆脱了传统CFD 方法对网格的依赖性，大大减少了计算量，同时可采用大时间步长，解析度高，十分适合解决高雷诺数下的涡发放和涡致运动问题。

本文采用NACA 66（MOD）水翼模型［36］，水翼弦长为0.72 m，最大厚度为弦长的10%，最大厚度位于距离前缘50%弦长处。NACA 66（MOD）水翼截面型式如图12 所示。

图12 NACA 系列水翼截面（最大厚度为弦长的10%）Fig.12 Section of NACA series hydrofoil（maximum thickness is 10% of chord length）

3.1 来流速度对涡发放频率的影响

应用离散涡法模拟NACA 66（MOD）水翼在不同流速中的涡发放情况，水翼的攻角为10°。通过对垂向载荷进行傅里叶变换，得到了雷诺数与涡发放频率的关系，如图13 所示。由图可见，随着雷诺数的增加，泄涡频率不断增加。然而，在不同的雷诺数区间，泄涡频率的增加速率不同，两者呈现非线性关系。在雷诺数为2.5×107～3.5×107区间，泄涡频率增加缓慢，这表明水翼在这一流速范围内会稳定发出低频噪声，此时泄涡频率在水翼结构固有频率（60 Hz）附近变化。

图13 雷诺数与涡发放频率关系Fig.13 Relationship between Reynolds number and vortex shedding frequency

对于不同雷诺数，同一时刻（t=0.4×C/U）下水翼绕流的尾流场涡量云图如图14 所示。从图中可以看出，雷诺数越大，新生涡运动至尾流场越快，与水翼后缘的距离越远，这是由于流体速度的增加会加快边界层附近流体的运动和分离，新生涡团在来流作用下快速发展并运动至尾流场，因此泄涡频率变大。

3.2 攻角对涡发放频率的影响

对上述NACA 66（MOD）水翼在5 种不同初始攻角情况下的泄涡过程进行模拟。攻角分别取为5°，7.5°，10°，12.5°和15°，来流速度约为14.0 m/s，对应的雷诺数为1.0×107。攻角与涡发放频率的关系如图15 所示。从图中可以看出，泄涡频率随攻角的增大而减小。当攻角小于10°时，泄涡频率在30～35 Hz 区间；当攻角大于10°之后，泄涡频率下降显著；当攻角为15°时，泄涡频率已降低到13.5 Hz。

在Re=1.0×107条件下，同一时刻（t=0.8×C/U）不同攻角下水翼绕流的涡强对比如图16 所示。从图中可以看出：随着水翼攻角的增加，泄涡尺寸和涡强不断增加，水翼纵摇运动的能量耗散越来越多；在相同流速（相同能量输入）情况下，泄涡变得更加缓慢，因此泄涡频率变小。

图14 流速与涡强的关系Fig.14 Relationship between flow velocity and vortex strength

图15 攻角与涡发放频率的关系（Re=1.0×107）Fig.15 Relationship between angle of attack and vortex shedding frequency（Re=1.0×107）

图16 攻角与涡强的关系（Re=1.0×107）Fig.16 Relationship between angle of attack and vortex strength（Re=1.0×107）

对5 个不同流速下，对应的雷诺数为0.5×107，1.0×107，2.0×107，3.0×107和4.0×107，各初始攻角的泄涡过程也同样进行了模拟，攻角与涡发放频率的关系如图17 所示。从图中可以看出：在同一流速下，泄涡频率随着攻角的增大而减小；在某一初始攻角下，随着流速的增加，泄涡频率同时增大，与上面得到的结论相符。