水下爆炸问题的数值模拟及离心机试验验证

2020-01-09刘世聪王秋生娄浩然

中国测试 2019年12期

刘世聪，王秋生，娄浩然

(北京工业大学建筑工程学院，北京 100124)

0 引言

水下爆炸研究在军事和民用建设方面都具有重要作用，其载荷主要包括两部分：冲击波以及气泡脉动，两者大约各占爆炸总能量的50%。水下爆炸研究初期，试验多以大当量炸药爆炸[1-2]和机理试验[3-4]为主，但在大多数机理试验过程中要忽略重力的影响，Takayama等[5]提出在冲击波阶段可以不考虑重力的影响，但气泡脉动阶段必须考虑。因此，考虑重力效应的缩比模型试验成为水下爆炸试验研究的主要方式，离心机水下爆炸便是缩比模型试验的一种，其利用离心机在水下形成超重力场，达到极少量炸药模拟原型大当量炸药的爆破效果。中国水利水电科学研究院已在离心机水下爆炸领域做了一些探索[6-7]。

随着计算机技术的不断进步，数值计算已成为研究炸药水中爆炸的重要手段之一。水的状态方程、人工粘性系数、网格尺寸都是影响数值计算精度的重要因素，针对这几个影响因素的分析，国内外已经进行了一系列的研究。李晓杰等[8]对不同水状态方程进行理论分析并提出了不同水状态方程的适用范围，然后通过数值模拟验证了理论分析的结果。Huang等[9]建立一维楔体中心对称模型，对不同药量的球形炸药水下爆炸进行了计算，研究了人工粘性系数对于水下冲击波的影响。Shi[10]等对比了空中爆炸模型在不同网格尺寸下的冲击波峰值、冲击波比冲量等数值计算结果及误差，提出了减小网格尺寸带来的误差的方法。但目前许多数值模拟研究缺少试验数据的验证，仅仅依靠数值计算本身很难具有普遍的适用性。

本文利用RDX（黑索金）炸药离心机水下爆炸相对应的数值模拟研究，首先验证了相似准则在数值模拟中的合理性，同时建立具有不同水状态方程、人工粘性系数、网格尺寸的模型，分析其对水下爆炸冲击波及气泡脉动数值计算结果的影响并提出了一些参数取值的建议，最后将数值计算结果与离心机水下爆炸试验数据对比，验证了水下爆炸冲击波及气泡脉动规律。

1 离心机水下爆炸试验

离心机水下爆炸试验是在中国水利水电科学研究院IWHR试验室的LXJ-4-450离心机（见图1）上进行的。随着离心机的转动，在水下形成一个比重力加速度g大很多倍的离心加速度N，忽略重力及假设离心加速度保持不变，小模型便实现了与原型一样的重力场环境，能以极少量炸药模拟原型大当量炸药水下爆炸效果。

图1 LXJ-4-450离心机

如图2所示，试验中，模型箱的内部尺寸为1 280 mm×720 mm×900 mm，模型箱内水体深度为600 mm，为提高试验精度，炸药采用特制的质量W为1 g 的RDX（黑索金）球形炸药，半径Re为5.25 mm，密度ρ为1.65 g/cm3，并将其至于水下300 mm处。在水下与炸药相同深度的平面内布置水压力传感器以获取冲击波数据，炸药与传感器之间的距离即爆距为L。侧向布置高速摄像机以捕捉水下爆炸气泡。试验分别在超重力环境20，30，40，50g下进行。左侧钢板的尺寸为700 mm×600 mm×50 mm，距离炸药300 mm，由厚为50 mm的混凝土支座固定，钢板用于研究结构的动态响应，不在本文详细描述，本文只是将其看成与模型箱外壳一样的边界。各试验工况如表1所示。

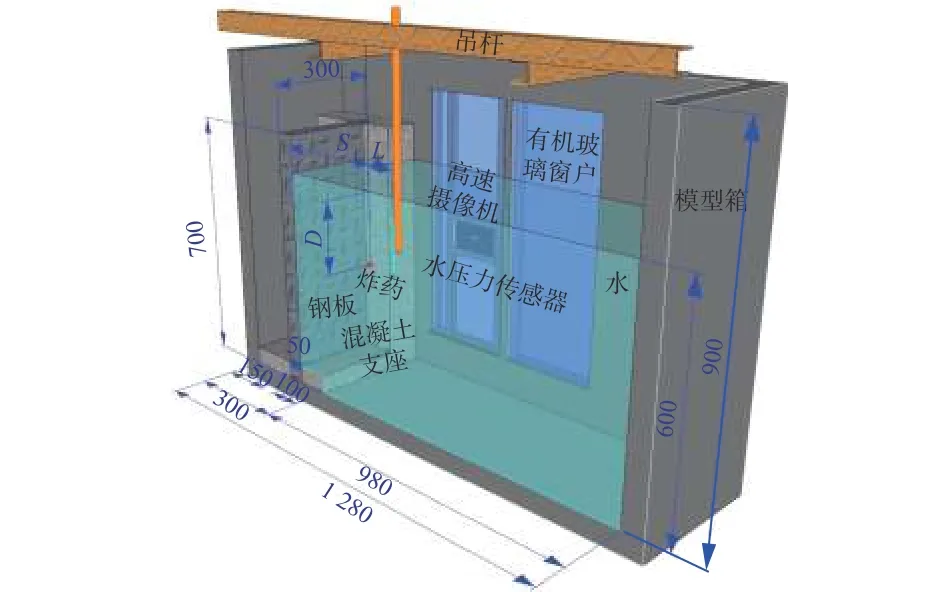
图2 试验模型箱（单位：mm）

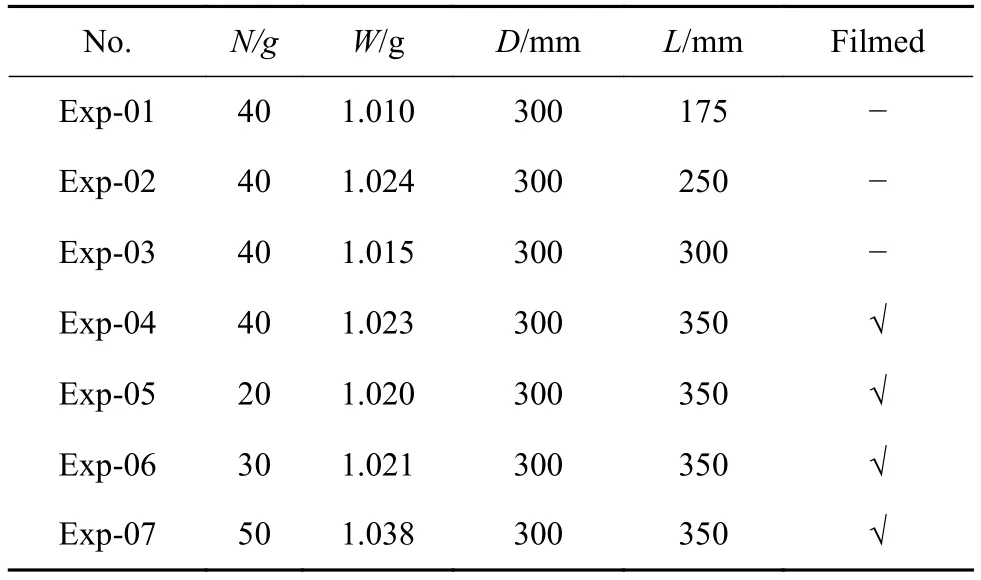
表1 试验工况

2 相似准则在水下爆炸数值计算中的验证

相似准则[11]是水下爆炸模型试验的理论基础。文献[6-7]对相似准则内容，及相似准则在离心机水下爆炸试验中的合理性进行了详细描述，本文不再赘述。表2列出了离心相似关系。

利用表2中的相似关系，将下文中的二维数值模型Num-2D-40g、三维数值模型Num-3D-40g换算至原型进行计算，并将原型计算结果与两模型利用相似关系换算至原型条件下的计算结果进行对比，如图3（a），图3（b）所示，发现每幅图中的两条曲线都基本重合，因此相似准则在数值计算中也是符合的。这为以离心机水下爆炸试验为基础而进行的数值计算提供了理论支持。

3 数值模拟

3.1 状态方程

状态方程是表征物体压强、密度、比内能3个参量的函数关系式。

空气采用理想气体状态方程[12]：

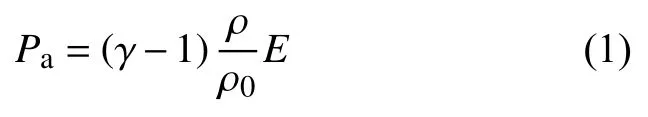
式中：Pa——空气压力，MPa；

γ——绝热指数，取1.4；

ρ0——空气的初始密度，取1.225 kg/m3；

ρ——空气密度，kg/m3；

E——空气的比内能，GJ/ m3。

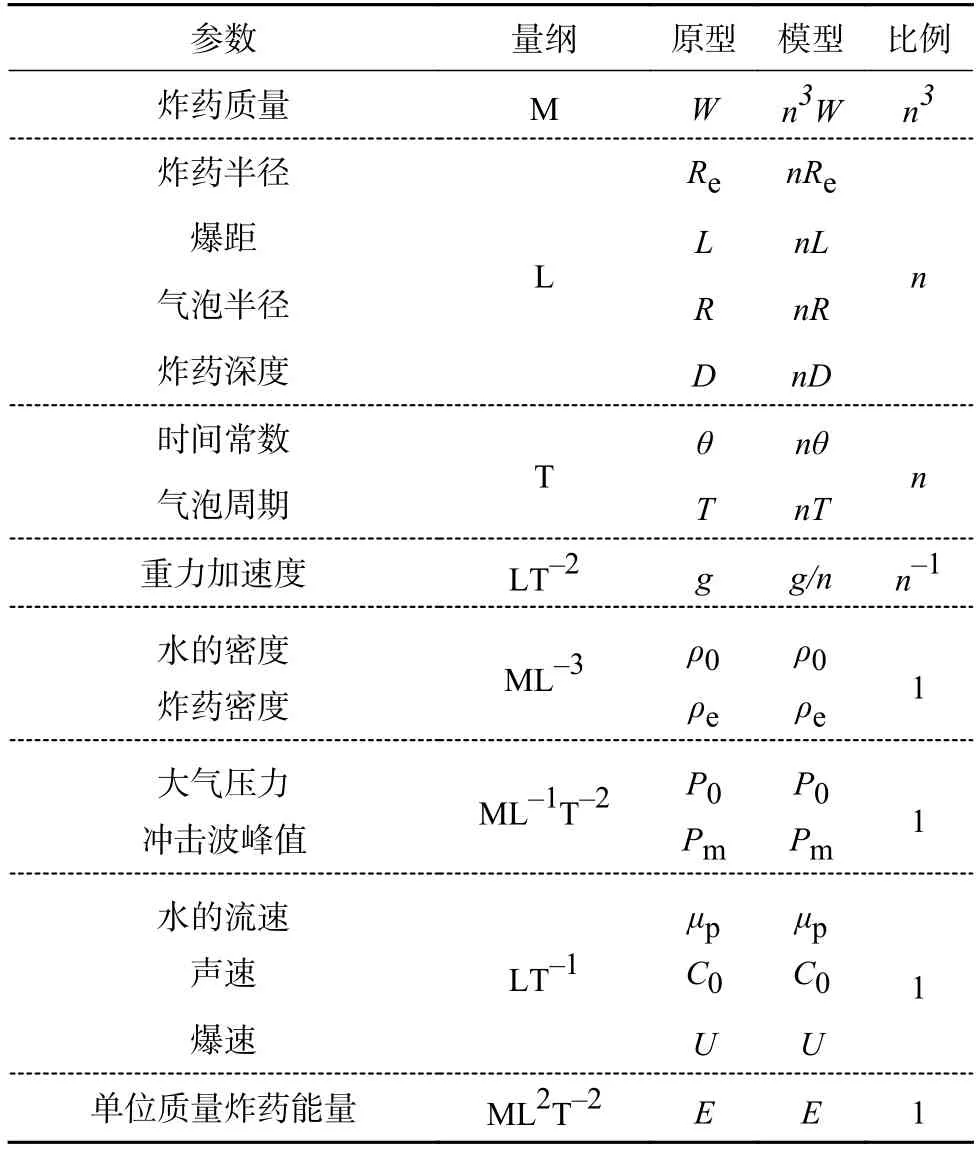
表2 离心相似关系

RDX炸药采用标准的JWL状态方程[12]：

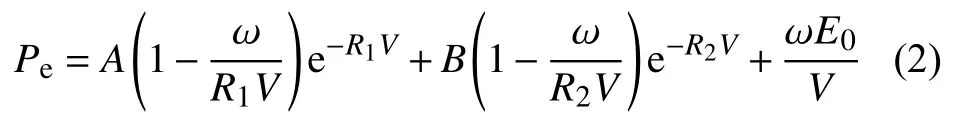
式中，A，B，R1，R2，ω为状态方程参数，A、B单位为GPa，R1，R2，ω为无量纲参数；Pe为爆轰产物的压力，MPa；V为相对体积，m3；E0为爆轰产物的初始比内能，GJ/m3；试验所用的炸药是专业研制的，因此需要利用一种半经验的方法[6]确定JWL状态方程的各参数。最终各参数取值A=565.295 GPa；B=1.217 11 GPa；R1=4.213 9；R2=1.137 75；ω=0.35；E0=9.536 GJ/m3。

水的状态方程有两种：Shock状态方程，多项式状态方程。Shock状态方程是以冲击Hugoniot点（PH，μ）表示的Mie-Grüneisen高压状态方程[8]：

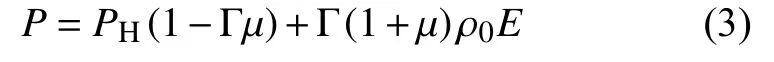
式中，μ为压缩比，其值为ρ/ρ0-1；ρ0为水的初始密度，为1 g/cm3；E为水单位质量的内能，GJ/m3；PH为冲击Hugoniot压力，单位MPa，为含μ的未知量函数，由冲击Hugoniot曲线确定；Г为Grüneisen系数，无量纲参数，同样是含μ的未知量函数，其值由常温常压下的Grüneisen系数Г0和Г的高压物理性质确定。Г表达式如下：

式中a为常数，是Г0的一阶体积修正常数。

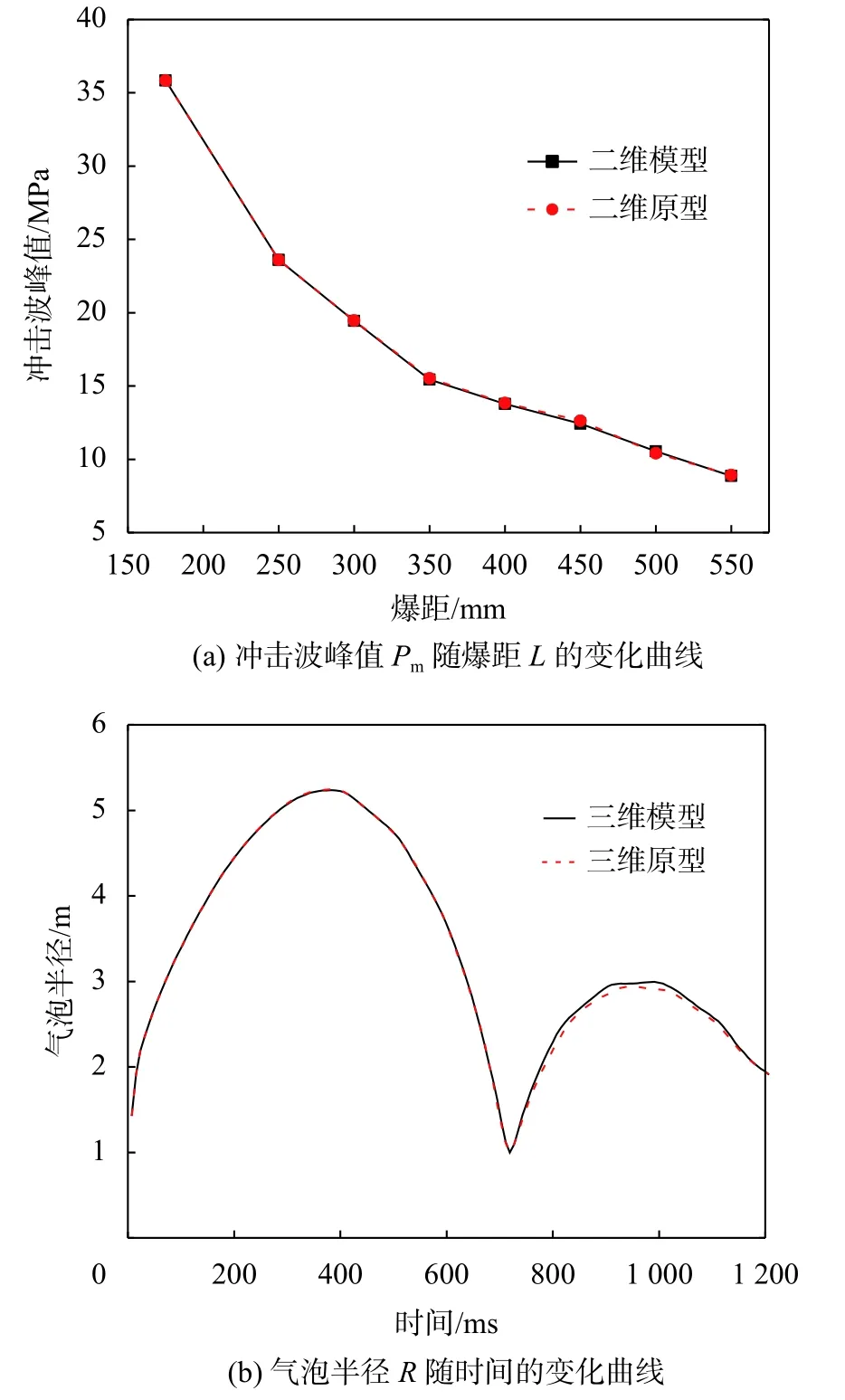
图3 原型与模型计算结果对比

在Shock状态方程中，冲击波速度U（km/s）与波后质点速度μp（km/s）看作线性关系，即

式中，k1为冲击波速度与波后质点速度成线性关系时的斜率，是经验系数；C0为常温常压无扰动状态声速，km/s。Shock状态方程参数取值为：Г0=0.28，a=0，k1=1.75，C0=1.483 km/s。

水的多项式状态方程[12]根据压缩状态的不同具有不同的形式。

当水压缩时（μ＞0），其状态方程：

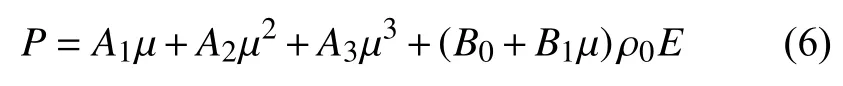
当水膨胀时（μ＜0），其状态方程：

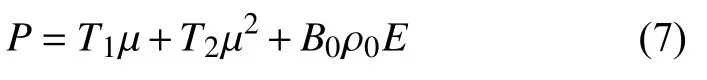
式中，E为水单位质量的内能，GJ/ m3；A1=2.2 GPa，A2=9.54 GPa，A3=1.457 GPa，T1=2.2 GPa，T2=0为压强量纲常数；B0=B1=0.28为无量纲常数。

3.2 数值模型

基于离心机水下爆炸试验，建立如图4、图5所示的模型进行计算。图4为二维模型Num-2D，用来研究历经时间短，精度要求高的冲击波，其采用轴对称方式建立。炸药质量为1 g，半径为5.25 mm，炸药、测点置于水下300 mm，在空气顶端施加流出边界，以刚性边界模拟试验的模型箱，水体、炸药、空气均采用Euler单元体建立。图5为三维模型Num-3D，用来研究历经时间长的气泡脉动，在建模时应用网格映射技术，将二维模型中冲击波刚要碰触边界时的计算结果映射到三维模型中继续计算。三维模型采用面对称方式建立，重力环境、单元体、边界的选取与二维模型一致。表3列出了数值模型工况。

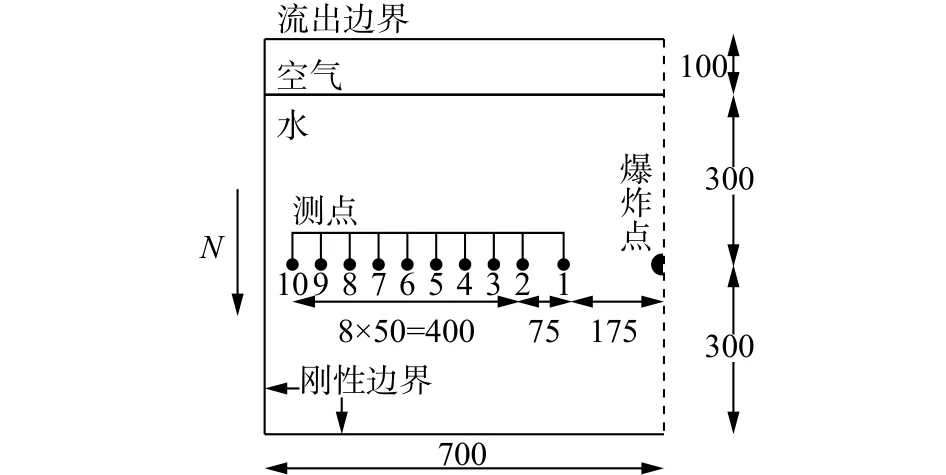
图4 二维模型Num-2D示意图（单位：mm）

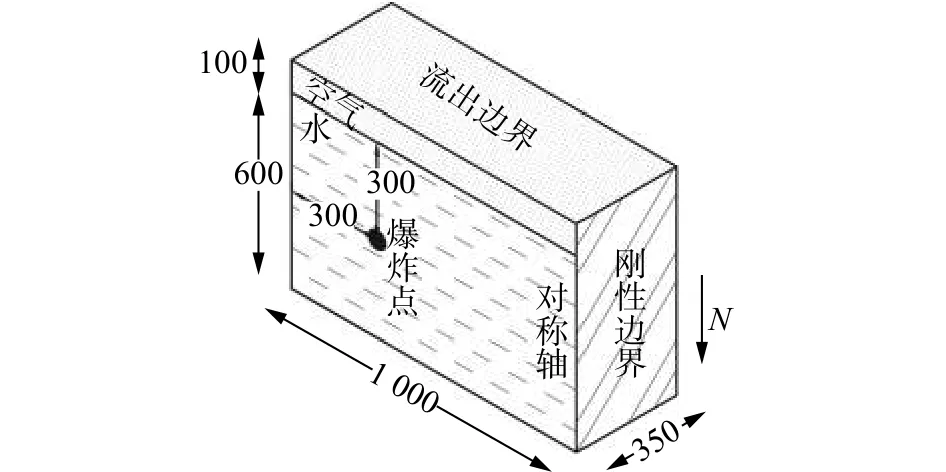
图5 三维模型Num-3D示意图（单位：mm）

3.3 影响数值计算精度的因素

3.3.1 水的状态方程

将二维模型Num-2D-40g、三维模型Num-3D-50g中的水体分别设置Shock与多项式两种状态方程来研究水的状态方程对冲击波及气泡脉动的影响。如图6所示，利用Shock状态方程计算出的冲击波峰值较多项式状态方程要大，且更贴近试验值。由于试验数据的限制，图中的试验曲线是利用Cole[1]提出的冲击波峰值Pm计算公式拟合得来，公式如下：

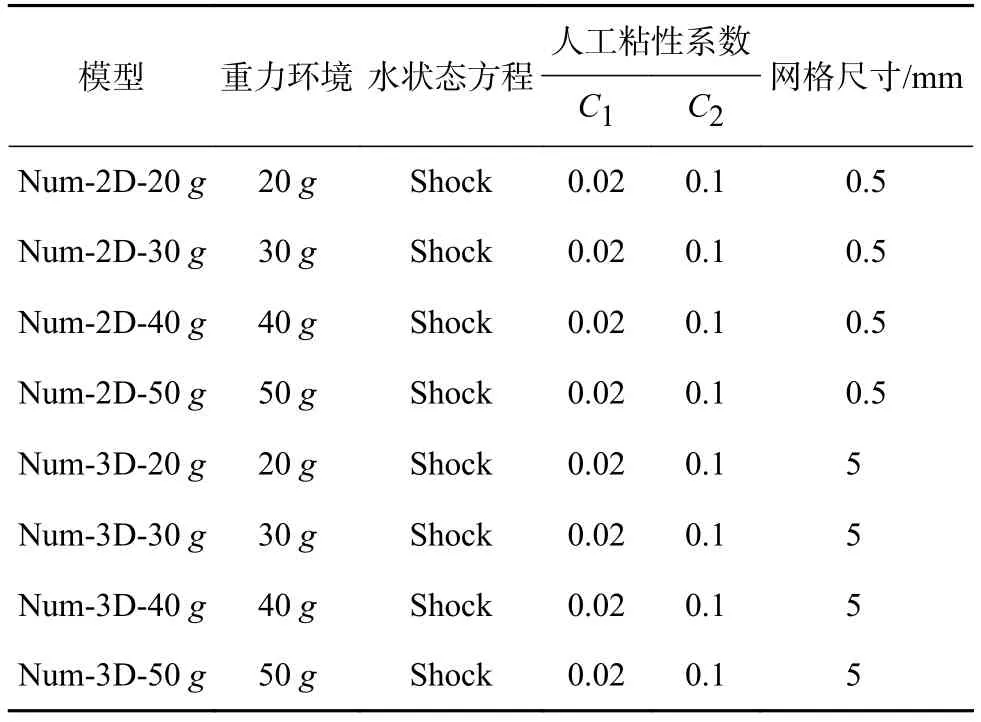
表3 数值模型工况

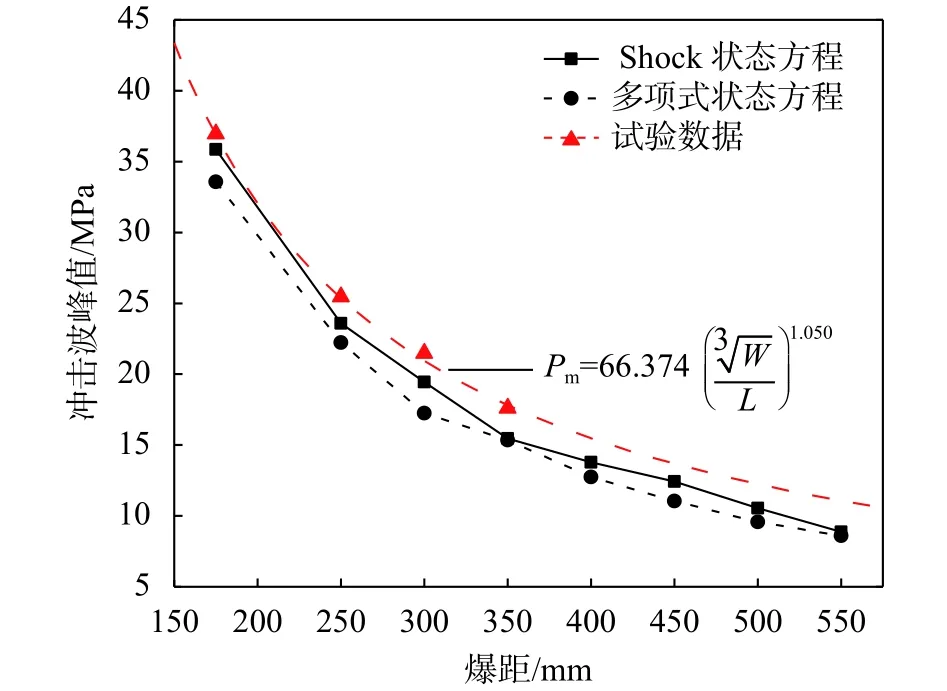
图6 两种状态方程下的冲击波峰值压力

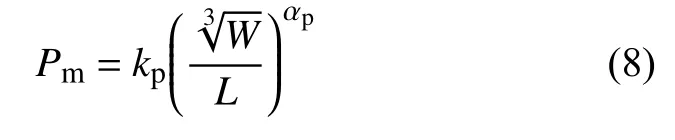
式中：W——炸药的质量，kg；

L——爆距，mm；

kp，αp——经验系数，与炸药种类有关，无量纲。

由表4对比发现，Rm，T几乎不受水状态方程的影响。因为多项式计算的水体压力略小于Shock状态方程，因此气泡最大半径Rm会比Shock计算的略大一些，但状态方程的不同并不影响气泡脉动周期的大小。

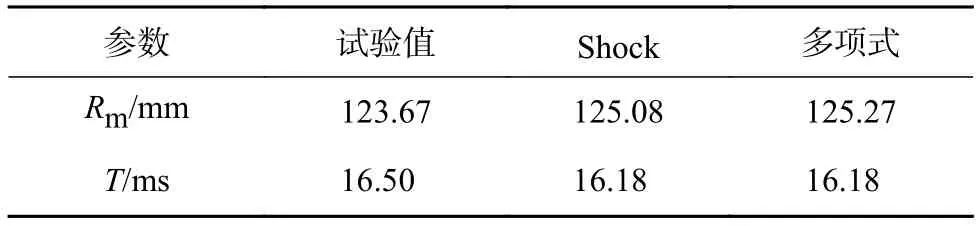
表4 不同水状态方程的Rm，T值

3.3.2 人工粘性系数

人工粘性系数是为了解决冲击波波阵面前后压力、密度等突变问题而引入的。有限元软件给出的人工粘性项系数如下式[13]所示：

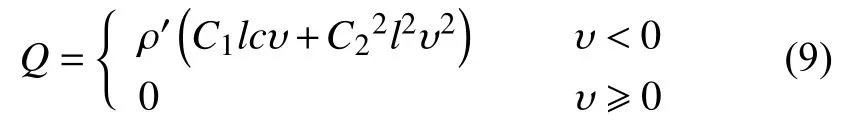
式中：C1——一次项人工粘性系数；

C2——二次项人工粘性系数；

l——计算单元长度；

ρ'——材料密度；

c——声速；

υ——体积变化率。

在二维模型Num-2D-40g中改变C1，C2取值来研究人工粘性系数对冲击波峰值的影响。取C2=0.1，将C1分别设置为0.002 5、0.005、0.01、0.02、0.05、0.10、0.15、0.20、0.25、0.30以此研究一次项人工粘性系数对计算结果的影响；对于二次项人工粘性系数的研究，取C1=0.02，将C2分别设置为0.025、0.05、0.1、0.25、0.5、0.75、1.0、1.25、1.5。在三维模型Num-3D-50g中分别设置C1=1.0，C2=0.02；C1=0.1，C2=0.2；C1=1.0，C2=0.2；C1=0.1，C2=0.02 4种情况研究人工粘性系数对气泡脉动的影响。

从表5可以看出，不同的C2对于冲击波峰值影响不大。如图7所示，当C1＞0.02，随着一次项粘性系数的增大，冲击波峰值逐渐减小，且各点与试验值之间的误差都大于10%。当C1＜0.02，冲击波峰值与一次项粘性系数之间并不成一定的规律性且计算值也非常接近，各测点误差均小于8%，因此在数值计算时建议C1＜0.02，以提高计算的精确度。

表6给出了三维模型Num-3D-50g取不同的人工粘性系数计算得来的Rm，T值。如表所示，只有当一次项人工粘性系数与二次项人工粘性系数都取较小的值时气泡最大半径Rm会略有减小，但是气泡脉动周期T没有变化。因此，建议在研究气泡脉动Rm及T时，可忽略人工粘性系数的影响。

3.3.3 网格尺寸

计算单元的网格尺寸d与炸药半径Re是两个重要的长度参数。因此，定义无参数量λ来描述单元网格的疏密程度，λ=Re/d。二维模型Num-2D-40g、三维模型Num-3D-40g的基础之上，改变网格尺寸以研究其对冲击波及气泡脉动计算结果的影响。将二维模型的网格尺寸分别取2，1.5，1.25，1，0.8，0.5，0.25，0.2，0.15 mm，对应的λ为2.625、3.5、4.2、5.25、6.562 5、10.5、21、26.25、35；三维网格尺寸分别取20，15，12，10，7.5，5，2.5 mm，对应的λ为0.262 5、0.35、0.437 5、0.525、0.7、1.05、2.1。为使本文对网格尺寸的研究工作更具适用性，对数值计算结果中的气泡半径Rn与脉动时间Tn采用无量纲化处理，使其与试验值进行对比，即R′=Rn/Rm，T′ =Tn/T，其中R′和T′ 为无量纲气泡半径与无量纲脉动时间。

图8给出了二维模型下λ与冲击波峰值Pm的关系曲线。图中与各测点Pm-λ曲线接近的4条虚线是该测点的试验值。可以看出，随着λ的增大，即网格尺寸的减小，Pm逐渐增大且趋于稳定，在λ=35时测点1（L=175 mm）已出现Pm减小的趋势。测点1在λ=10.5时与试验值最接近，测点2（L=250 mm）在λ=21时，而测点3（L=300 mm）、测点4（L=350 mm）就目前计算情况来看，则在λ=35时与试验值最接近。因此，爆距L的不同对网格尺寸取值要求也不一样。爆距近的点，在网格相对稀疏时便可使计算误差达到允许范围，爆距越远，要求网格尺寸则越小。因此，建议二维网格尺寸d=（1/30~1/10）Re。

图9给出了三维模型下R′、T′ 与λ的关系曲线。可以看出，随着λ的增大，即网格尺寸d逐渐减小，气泡最大半径Rm、脉动周期T与相应试验值逐渐接近，但并非网格尺寸越小越接近。当网格尺寸与炸药半径大小相近，即λ=1.05时，数值计算的气泡最大半径和脉动周期与试验值最接近，之后随着网格尺寸的减小，如图中λ=2.1，即网格尺寸约取炸药半径的1/2时，数值计算的气泡半径与脉动周期虽都有所增加，但增幅不大，且数值计算时间会大大增加。

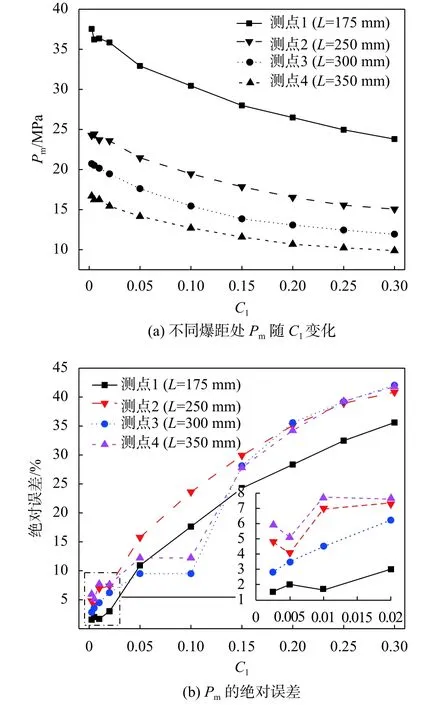
图7 不同 C1 计算结果对比

表6 50 g下不同C1，C2的气泡最大半径与脉动周期值

图10给出了不同λ下的第二脉动周期气泡面积S与时间的关系曲线。由图可以看出，网格尺寸d越小，第二周期的气泡最大面积Sm也越大，当λ＞0.525时，即网格尺寸大于炸药半径的2倍时，整个第二脉动周期气泡面积变化不大，且第二、三次脉动周期之间的临界点不明显；λ＜0.525时，可以观察到气泡大小变化，且可找出不同周期之间的临界点；在与炸药半径相近时（ λ= 1），计算结果与试验结果误差最小。

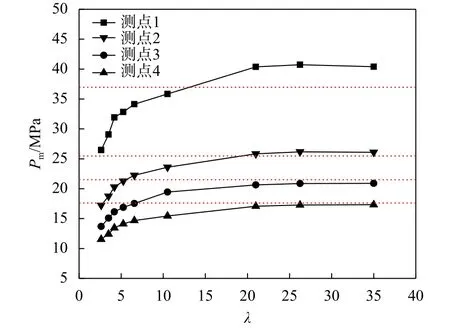
图8 不同网格尺寸下各测点的Pm- λ曲线

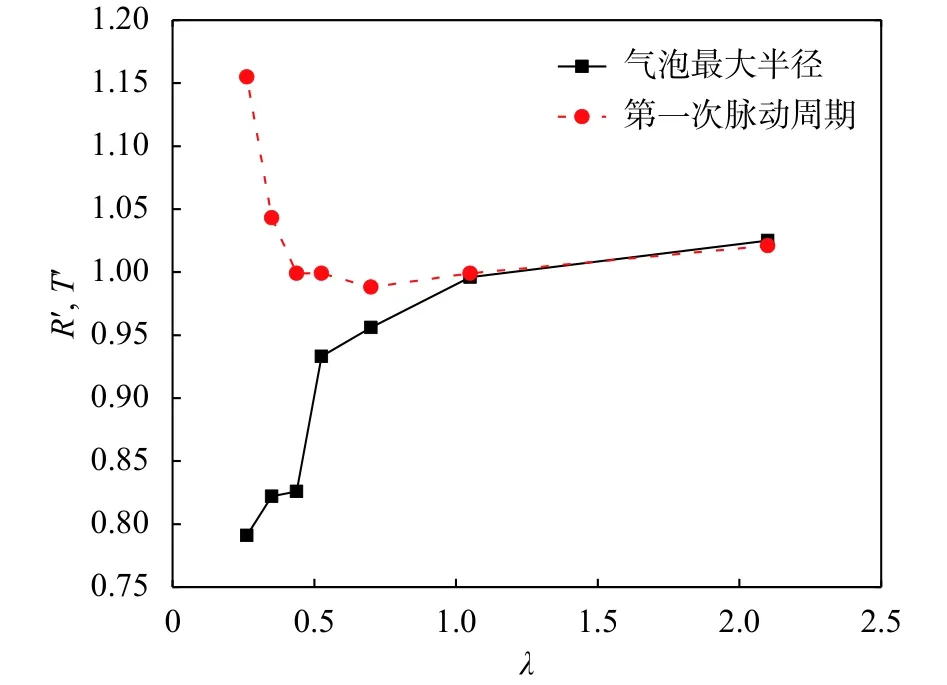
图9 不同网格尺寸下的R'/ T'-λ曲线

综合上述分析，若要利用三维模型研究气泡脉动，建议网格尺寸近似取与炸药半径Re相近的尺寸。

4 离心机水下爆炸试验验证

依据前文的总结，利用Num-2D，Num-3D进行各个重力加速度下的数值模拟计算。通过以上分析，水状态方程选取Shock状态方程，令C1=0.02，C2=0.1，二维网格尺寸选取0.5 mm，三维网格尺寸选取5 mm。水压力传感器测得的各试验工况下的冲击波压力曲线[6]如图11所示。数值模拟各试验工况得来的冲击波压力曲线如图12所示，因为人工粘性系数的设置，导致冲击波后出现伪振荡[13]。

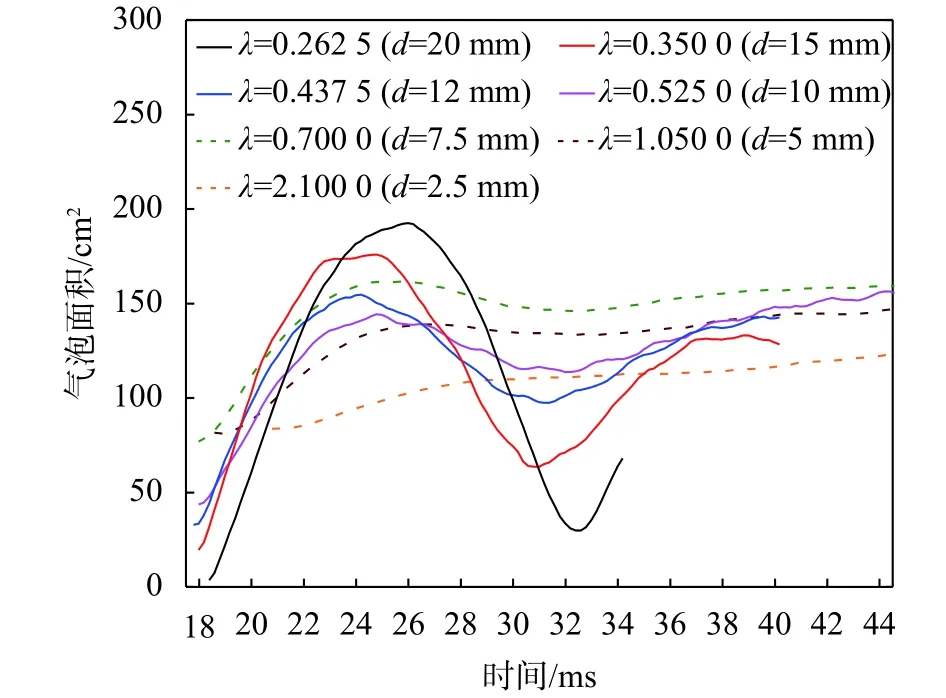
图10 不同λ下的第二周期气泡面积与脉动时间曲线

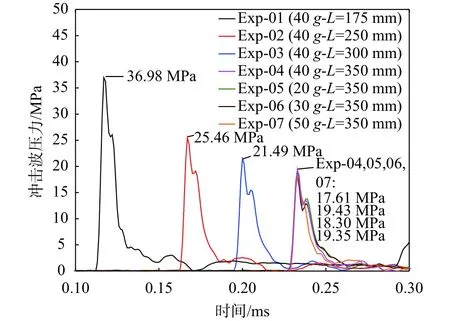
图11 试验冲击波压力曲线

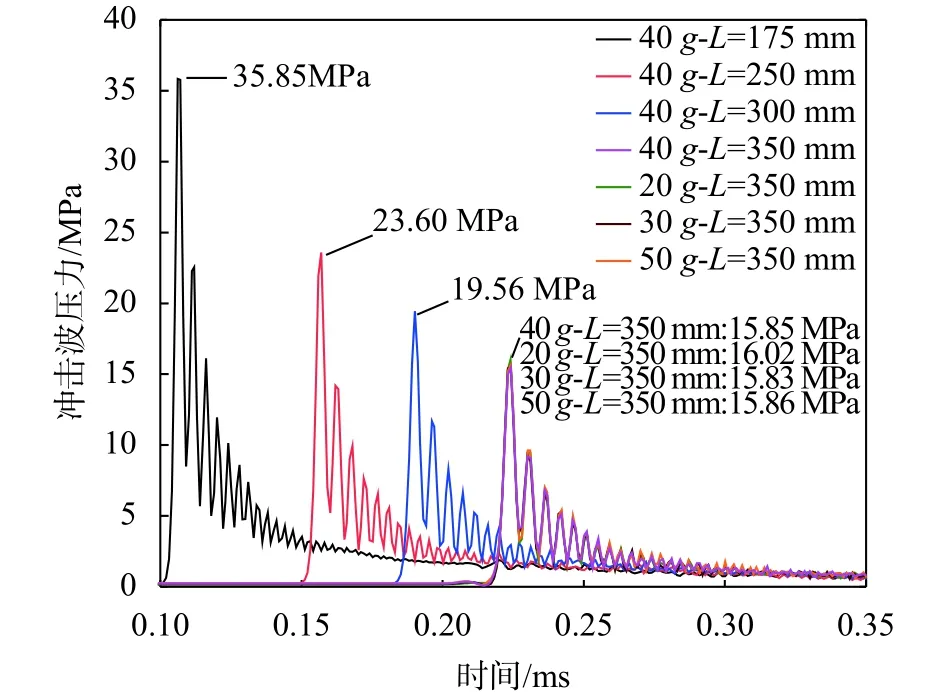
图12 数值冲击波压力曲线

从试验及数值结果可以看出，随着爆距L的增大，冲击波峰值Pm是逐渐减小的。Exp-04到Exp-07是在不同的超重力加速度下进行的，但四者的冲击波波型基本一致，且数值计算中四者的数值模拟结果相差也很小，这说明在研究冲击波峰值时可以忽略重力影响，同时也证明了文献[5]的结论。

高速摄像机拍摄以及利用三维模型数值计算的40g下气泡第一周期过程图如图13 所示，表7为试验所得数据[6]及数值计算的气泡最大半径Rm以及脉动周期T的对比。由于高速摄像机拍摄范围的限制，在气泡膨胀过程中，有些气泡已经超出拍摄范围，但本文的气泡外形仍以完整圆处理。

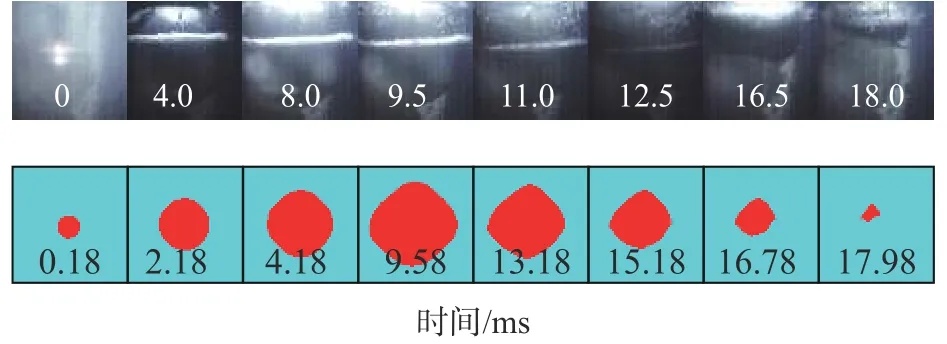
图13 40 g下第一周期气泡运行形态

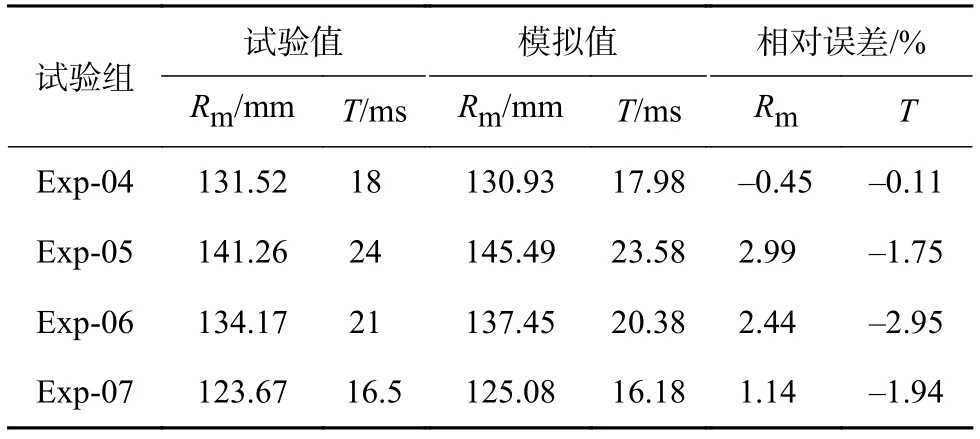
表7 各重力条件下Rm及T试验与数值结果对比

如图13 所示，40g下试验（Exp-4）气泡在9.5 ms膨胀至最大，数值在9.58 ms膨胀至最大，膨胀过程中呈球形，收缩时逐渐变为纺锤形，试验在18.0 ms收缩至最小，数值在17.98 ms收缩至最小。数值计算得到的Rm和T与各自的试验值误差都较小，均在3% 以内。可以得出结论：气泡脉动必须考虑重力作用，且随着重力加速度的增大，气泡最大半径Rm以及脉动周期T都是在减小的，也验证了文献[5]的结论。