Target-enclosing aきne formation control of two-layer networked spacecraft with collision avoidance

Yng XU, Delin LUO, Dongyu LI, Ynheng YOU,*, Hiin DUAN

a School of Aerospace Engineering, Xiamen University, Xiamen 361005, China

b Department of Control Science and Engineering, Harbin Institute of Technology, Harbin 150001, China

c State Key Laboratory of Virtual Reality Technology and Systems, School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China

d Department of Electrical & Computer Engineering, National University of Singapore, Singapore 117583, Singapore

Abstract This paper addresses a target-enclosing problem for multiple spacecraft systems by proposing a two-layer affine formation control strategy. Compared with the existing methods,the adopted two-layer network structure in this paper is generally directed, which is suitable for practical space missions.Firstly,distributed finite-time sliding-mode estimators and formation controllers in both layers are designed separately to improve the flexibility of the formation control system.By introducing the properties of affine transformation into formation control protocol design,the controllers can be used to track different time-varying target formation patterns.Besides,multilayer time-varying encirclements can be achieved with particular shapes to surround the moving target. In the sequel, by integrating adaptive neural networks and specialized artificial potential functions into backstepping controllers, the problems of uncertain Euler-Lagrange models, collision avoidance as well as formation reconfiguration are solved simultaneously. The stability of the proposed controllers is verified by the Lyapunov direct method. Finally, two simulation examples of triangle formation and more complex hexagon formation are presented to illustrate the feasibility of the theoretical results.

KEYWORDS Affine formation control;Collision avoidance;Lyapunov stability;Target enclosing;Two-layer strategy

1. Introduction

Compared with using one single spacecraft, using multiple spacecraft in formation flight to constitute a large space mission system has many advantages,such as stronger robustness,higher efficiency, and lower cost. Various space projects for multiple spacecraft formations have been launched during the past decades, e.g., PRISMA,1TerraSAR-X2and TanDEM-X.3As an important goal of space missions in recent years, enclosing a target of interest has exhibited a promising application of multiple spacecraft formations from a civilian or military perspective.4-8

As an insufficiently solved topic of cooperative control,the target-enclosing problem requires all the spacecraft to form a configuration surrounding a specific relatively static or dynamic target. One central issue in target-enclosing is target tracking, which has been studied extensively for the relatively stationary target case.9-12Previous researchers have also made many contributions to the moving target tracking control, e.g.,13-15The other key issue in targetenclosing is the formation control16,17or the formationcontainment control.18,19A time-varying formation pattern that multiple followers rotate around the single static leader is demonstrated in Ref.20. Ref.21tackles a time-varying formation pattern, which shows that multiple followers rotate around multiple moving leaders. The problem of multiple leaders rotating around multiple followers is analyzed in Refs.22,23. Since Ref.20is the case of tracking a single leader,it fails to satisfy the condition of existing multiple leaders.Although multiple leaders occur in Refs.21-23, leaders and followers, respectively, cannot achieve the required formation shapes simultaneously. Till now, there exists an acceptable solution inspired a new coordinated control method called two-layer formation-containment control scheme.24The leader-following structure integrated with a virtual leader is adopted, in which the formation of leaders and the containment of followers are required to be achieved simultaneously. However, the containment control of followers cannot be used to form a particular shape, and the positions are randomly localized inside the convex hull of leaders.Thus, this control approach is not reliable for the proposed target enclosing task. Most of the existing works listed in the recent survey25focus on the situations in the presence of a constant single-layer formation. However, to formulate the multiple time-varying encirclements for a moving target,the control strategy becomes much more challenging, and no referential experience is available.

Equipped with different sensors, nowadays position-based,displacement-based, distance-based and bearing-based strategies are becoming four dominant solutions to the problems of spacecraft formation control.26,27By regarding the measured signals as the constraints, various target formation patterns can be designed. However, none of them can achieve tracking time-varying formation translations,scales and orientations simultaneously. Geometric transformations can map points between different spaces. These transformations may be simple, such as scaling each axis, or complex, such as nonlinear twists or bends.28Among them, linear transformations are capable of being expressed by matrix operations easily,29which deserve to be introduced into the problem of formation control.In general,an affine transformation,as a linear transformation, can be seen as a composition of rotations, translations, dilations, and shears. The affine transformation preserves collinearity and ratios of distances.30Besides, this transformation is convexity-preserving,which is a useful property in analyzing the task of target capture.Recently,an affine formation control is proposed,31,32such that various target formation patterns based on the affine transformation can be mutually transformed.

A critical issue for multiple spacecraft formation control is to avoid the collision with each other and with other unexpectedly emergent threats in the space. After avoiding inter-agent collisions and pop-up obstacles, the spacecraft formation needs to be reconfigured to encircle the moving target again.During the past decade,numerous studies have been published on tackling these topics.33-36A behavioral control approach using the null-space based concept is proposed in Ref.33, the aims of removing neighboring spacecraft collisions and reconfiguring the formation are accomplished. Ref.35proposes a sequential optimization algorithm to avoid inter-spacecraft collisions, then a semianalytic approach is applied to dealing with the formation reconfiguration.Another switching control algorithm under constant thrust is adopted to achieve collision-free maneuvers in Ref.35, and the target positions to be relocalized can be calculated by an isochronous interpolation method. Research results in Ref.36, the controller is integrated with the neural network-based reconfiguration algorithm, and a modified null-space based behavioral avoiding scheme is merged. Unfortunately, few of the approaches mentioned above have considered the collision-free problem in a target-enclosing mission, meanwhile independent dodging protocols are constructed and most of the spacecraft formations are regarded to be rigid. An artificial potential function holds the particular characteristic of approximating infinity via approaching the limits of arguments, and this function can be specialized and act as a good tool to prevent collisions and smooth control inputs.17In the field of aerospace engineering, the models of spacecraft possess the properties as the Euler-Lagrange (EL) systems with the parametric uncertainties, which require the linearity-in-parameters assumption.37Besides, adaptive Neural Network (NN) backstepping control techniques are verified practically for tracking control problems of uncertain complex nonlinear or parameter strictfeedback form systems.38Therein, NNs’ universal approximation properties are very effective for modeling.

The main contributions of this paper can be stated as follows:

(A) A novel two-layer structure is adopted in the targetenclosing problems. By separating the Distributed Finite-time Sliding-mode Estimators (DFSEs) and formation controllers in both layers, which brings the flexibility of protocols design. Compared with the former deficiency of formation-containment control for randomly localizing followers, the proposed two-layer target-enclosing affine formation control can configure multi-layer time-varying encirclements surrounding a moving target and the followers can also form particular shapes.

(B) The properties of affine transformation are introduced to the design of controllers, and we extend the undirected graphical condition in to more general directed cases. Different from the requirement in our previous work, here the network between followers in the second layer can be generally directed, and the formation patterns can also be time-varying.

(C) The adaptive NNs and specialized artificial potential functions are integrated into the backstepping controllers, with which both uncertainties in EL spacecraft models, as well as collision avoidance and formation reconfiguration in the unknown space environment,are tackled together. All error signals can be contained within a small compact set,and the semi-global uniform ultimate boundedness is proved by the Lyapunov direct method.

The rest of this paper is organized as follows. In Section 2,the preliminaries and the problem statement are given. Section 3 provides the graphical condition of the affine localizability and the relation with the convexity. The main results are shown in Sections 4 and 5, where the two-layer targetenclosing affine formation control laws are designed by taking account of collision avoidance,and the stability of these protocols is also certified. In Section 6, simulations based on different formation requirements are carried out,and a conclusion is drawn in Section 7.

Notations: Throughout this paper, R represents the set of real numbers. Let Indenote the n-dimensional identity matrix,1nthe vector with all entries equal to one.Set λmax(·)and λmin(·)as the maximum and minimum eigenvalues of a matrix respectively, set σmin(·) and σmax(·) as the maximum and minimum singular values of a matrix respectively. Set ||·||1and ||·||2as the 1-norm or 2-norm respectively, |·| as the absolute value.Let diag（x1，x2，···，xn）∈Rn×nbe a diagonal matrix, where x1，x2，···，xnare the diagonal entries. sgn(·) denotes the signum function.

2. Preliminaries and problem statement

2.1. Graph theory

Fig.1 Examples of 2-reachable and non 2-reachable directed graphs.

Thus the set U can be seen as the root set R. The directed graph in Fig.1(a)is 2-rooted,and it also has a spanning 2-tree.

We here import a special Laplacian matrix named a signed Laplacian matrix.A signed Laplacian matrix Lsis a Laplacian matrix with both positive and negative real off-diagonal entries. The structure of Lsassociated to a directed graph can be defined as

where ωij∈R may be a positive or negative real weight attributed on the edge(j,i),and Lsis normally a asymmetric matrix.

2.2. Spacecraft dynamic

The spacecraft i in this paper is modelled by the following EL equation

where qi∈Rdrepresents the position vector of spacecraft i,Mi（qi）∈Rd×dis the symmetric positive definite inertia matrix,Ci（qi，q˙i）∈Rd×ddenotes the Coriolis centrifugal matrix,gi（qi）∈Rdis the gravitational force, and τi∈Rddenotes the control input.In the sequel,we give the properties of EL equation as.39

Property 1. For any spacecraft i, Mi（qi） is symmetric and positive definite.

Property 2. For any spacecraft i, Miqi（ ） is bounded with

where kmandare positive constants.

Denote xi,yi,zias the relative x,y,and z coordinate of the ith spacecraft in the Local-Vertical-Horizontal (LVLH) rotating frame respectively, and τix, τiy, τizare the corresponding three-axis control inputs. The expression of spacecraft model is provided as

Then, the formulation of EL model (Eq. (2)) contains Mi=miI3,

2.3. Collision avoidance and potential functions

Denote Hias the set containing all the spacecraft within the danger range rdangerof spacecraft i as

where ιi，j=ιj，iis a positive constant.

Define the repulsive region RPi（.）:R2→R as the interior of a circle stationary obstacle centred at position qowith radius ro, which can be expressed as

where Γiis a positive constant and dsafeis the required minimum safe distance. If there exist multiple obstacles within the radius ro, we denote them as a set O and o ∈O.

2.4. Problem formulation

We consider a group of n mobile spacecraft in Rd,and assume d ≥2 and n ≥d+2. These spacecraft exchange information by a directed graph G. The directed graph G containing n nodes represents the interaction topology of the group of spacecraft, an edge (j,i) shows that spacecraft i can measure the relative position of spacecraft j.

Denote the first nℓof spacecraft as the leaders and the rest nf=n-nℓas the followers. Thus the leaders’ subset is Vℓ= ｛1，2，···，nℓ｝ and the followers’ subset terms Vf=VVℓ. The leaders do not interact with the following spacecraft and do not need to access the information from these followers. Here we give an assumption for the leaders’acceleration constraints.

Assumption 1. The leaders are independent of the followers.There exists a positive constant δL, which satisfies

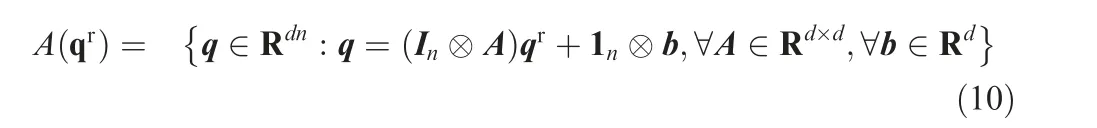
where （A，b） is the affine transformation.

where Lℓ1denotes the interaction topology related matrix among the leaders,is the corresponding interaction topology associated matrix among the followers,andis the interaction topology matrix between the leaders and the followers.For the convenience of analysis, we define a virtual agent 0,whose information is equal to the desired formation （G，qℓ）for the leaders. Then, definewhere ai0>0，i=1，2，···，nℓif the leaders can access to the desired formation information and ai0=0 otherwise. Before moving forward, define the interaction topology G0as the interaction between the virtual agent 0 and the leaders. Here,we present an assumption of the interaction relationship between the virtual agent 0 and the leaders.

Assumption 2. For the nℓleaders, the interaction topology G0has a directed spanning tree with the root of the virtual agent 0.

With Assumption 2, the property of Laplacian matrix is listed as below.40

Then, we define the affine localizability and the target formation.

Definition 1. The nominal formation （G，qr） is said to be affinely localizable if both of the following conditions are satisfied:

ii) For G and q, there exists a signed Laplacian Ls∈Rn×nassociated with G such that the equilibrium set satisfies

Definition 2. The target formation （G，q（t ））has the expression of

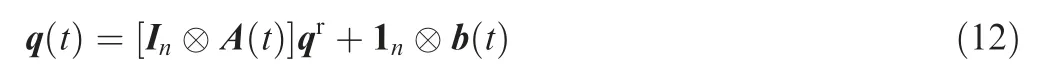
where A（t ）∈Rd×dand b（t ）∈Rdare continuous of t and may be constant or time-varying, if the time-varying target can be tracked successfully, q（t ） is in A（qr） for all t.

Finally, we propose a two-layer structure for the multiple spacecraft systems.

Definition 3. A two-layer leader-following structure is designed to describe the distributed affine formation tracking control problem:

(1) The first layer is for the leaders’ formation control, in which the leaders are supposed to achieve a specific formation and track the desired trajectories simultaneously,and the associated ordinary Laplacian matrix is

(2) In the second layer, the followers are supposed to be affinely localized by the leaders to track the target formation continuously, where the associated signed Laplacian matrix is

Up to now, the objective of this paper is to design a twolayer affine formation tracking control strategy such that all the spacecraft can converge to a moving target without collisions between inter-spacecraft as well as obstacles on the track.

3. Affine localizability and convexity

In this section,we will present the sufficient and necessary conditions of the affine localizability and the relations between the affine transformation and convexity.

Along with corresponding proof of Theorem 1 in Ref.in,33now an assumption of the nominal formation should be given.

After obtaining the assumption above, we modify Theorem 1 in our previous work41as following Theorem 1 to present the necessary and sufficient conditions to fulfill the affine localizability.

Theorem 1. Under Assumption 3, the affine localizability of the given nominal formation （G，qr） of n spacecraft can be achieved if and only if G is (d+1)-rooted and d+1 roots are leaders.

Proof. The corresponding proof is similar to Theorem 142and thus omitted here.

Now, another assumption is given about the affine localizability of the nominal formation.

Assumption 4. Assume that the given nominal formation（G，qr） can achieve the affine localizability.

Assumption 3 needs that both the nominal formation of agents and the subformation of leaders are d-dimensional affine span such that the dimension of A（qr） is a linear space of d2+d. Assumption 4 needs that there exists d+1 leaders in the leaders’ subset Vℓ, and each follower is (d+1)-reachable from Vℓ. Both of Assumptions 3 and 4 imply an important mathematical premise: The block of the signed Laplacian matrixis nonsingular.In the light of above Theorem 1, it can be found that

In the sequel, we present the relations between the affine transformation and the convexity.

Lemma 242. The convex hull has the following properties: i)if χ ∈Rd,then Conv（χ ）is a convex subset of Rd;ii)if χ is convex,then χ=Conv（χ ）;iii) if χ ⊂γ ⊂Rd,then Conv（χ ）⊂Conv（γ ）.

Theorem 242. If χ ∈Rdand f［.］ is an affine transformation of Rd, then f［.］ maps Conv（χ ） onto Conv（f ［χ ］）.

With above Lemma 2 and Theorem 2, we can provide the following Corollary 1. Besides, the proof is trivial and thus omitted here.

Corollary 1. If χ ⊂γ ⊂Rdand f［.］is an affine transformation of Rd, then f［.］ respectively maps Conv（χ ） onto Conv（f ［χ ］） and Conv（γ ） onto Conv（f ［γ ］） such that Conv（f ［χ ］）⊂Conv（f ［γ ］）.

For the simplicity, we assume that all the spacecraft move in a 2D workspace in the following parts of this paper.According to the property of the affine localizability, we can obtain that there are exactly 3 leaders in 2D plane. Meanwhile, by the properties of the convex hull and Assumption 3, one has that 3 leaders and 4 followers respectively in 2D plane can formulate a convex hull of a triangle and a rectangle with two circumscribed circles as Fig. 2(a), and these two circles are concentric. Also, we assume that there exist at least 4 spacecraft (leaders and several followers) can constitute a polygon with a circumscribed circle as Fig.2(b),and these two circumscribed circles also have the same center. Without loss of generality, we extend the condition to appearing multi-layer convex hulls as Fig. 2(c), more than two concentric circles exist.

Assumption 5. Assume that the given nominal formation（G，qr） of n spacecraft in 2D plane satisfies the leaders and followers can formulate two convex hulls in 2D plane. One largest convex hull with leaders has a circumscribed circle and contains the smaller convex hulls circumscribed by concentric circles,and the smallest convex hull encircles the circumcenter.

Remark 1. If several followers constitute the largest convex hull together with the leaders, these followers can be seen as pseudo leaders. In such a case, the affine formation control is similar to the two-layer formation-containment control.

Remark 2. The triangle has two properties:(A)arbitrary triangle can be affinely transformed form another triangle in the 2D plane; (B) arbitrary triangle has a circumscribed circle in the 2D plane. Assumption 5 guarantees that the convex hulls can enclose the center of circumscribed circles, and the scaling property of affine transformation can be applied.

4. First layer - distributed target tracking control for leaders

In this section,we would tackle the distributed target tracking problem for the leaders in the first layer modeled by EL with state feedback. These leaders under proposed DFSE protocol can obtain the desired position and velocity information in the finite time. The NNs are applied to compensate for the uncertainties of modeling, which can improve the system performance.

Under Assumption 1, we firstly propose the following DFSE algorithm for the ith leader with i=1，2，···，nℓ

where β1,β2are positive constants,^qi,^viare the estimations of the desired formation position, velocity of the ith leader respectively, ξiis the intermediate variable, and the formation position hi0is the formation function which denotes the time-

Fig.2 Examples of convex hulls formed by leaders and followers.

varying relative distance decomposed from the desired formation configuration. Suppose that all of leaders have the same value‖hi0‖2.The purpose of this paper is to track and contain a dynamic target with position qdand velocity ˙qd.It needs to be noted that the virtual agent 0 satisfies ^q0=qd, ^v0= ˙qd, which are the position, velocity of the moving target respectively.Then, we define the formation configuration of the leaders as

Lemma 343. For any positive real number c and α ∈ （0 ，1）, the origin of one Lyapunov function V （x ） is finite time stable if the inequality holds

where the estimated settling time is

With Lemmas 1 and 3, we put forward the following Theorem 3.

Theorem 3. There exist two positive constants β1and β2. If Assumptions 1 and 2 hold, with Eqs. (15)-(17), the leaders can achieve the accurate estimations of the position and velocity of the desired formation in the finite time respectively, which leads to

Before moving forward, we tackleas below

By differentiating V1, one has

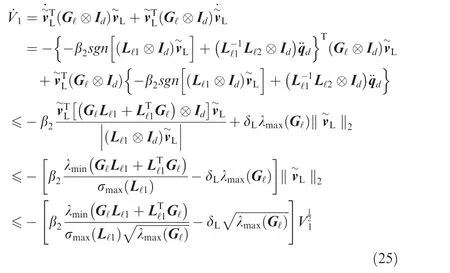
where only if

where it is easy to check β2>0 is satisfied, and the convergence ofhas been proved. Similar to this procedure, the errorcan be also verified to converge to origin.Then, we can obtain two finite time periods

Before moving forward,we define the following two generalized tracking errors for the leaders i ∈Vℓas

where α1iis the virtual control.

Then, with the EL model (Eq. (2)) of the ith spacecraft, by taking the time derivative of Eqs. (29) and (30) one has

Consider the following general potential function of the ith leader as

By taking the derivative of Vpi, one has

Since the potential function Pi，jbetween the neighboring spacecraft is bi-directional, after being multiplied by ˙z1i, we can obtain the partial derivative term

Let the virtual control has the expression as

where k1iis a positive constant,

and

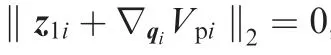
Then, from Eq. (31) we can deduce

By introducing the Gaussian functions, the entries for r=1，2，···，l of the activation function are expressed as

where ηris the width of the Gaussian function, and μris the receptive filed center.

In the sequel, we give the following distributed tracking control protocol and the adaptive law for the leaders in the first layer as

where Kidenotes the positive diagonal gain matrix,is the kth column vector of the NN estimated matrixfor k=1，2，···，d,γiand θiare the positive constants.Meanwhile,the weight error is defined as

Lemma 4. Let V（t ）≥0 as a continuously differentiable function with t>0 and V（0 ） bounded. If the following inequality holds

where c1＞0, c2are constants, then V(t) is bounded.

Proof. Consider the following Lyapunov function candidate for i ∈Vℓas

Taking the derivative of V3i, one has

With Property 1 and Eq. (39), and with control and adaptive algorithms as Eqs.(42)and(43),Eq.(49)can be rewritten as

We notice that

and

In the sequel, one has

Therefore, with Lemma 4 we have

where

and

To guarantee ϖi>0, we choose the control gain matrix Kifor i ∈Vℓsuch that

Here, we present the details of the proof such that z1i, z2iandare SGUUB.

where ,and z1can remain inside the compact set Ωz1. Then, the compact sets for z2andcan be proved with the similar procedure. The proof of Theorem 4 completes here.

Remark 3. If there exist constant formation positions hi0and hj0making hij=hi0-hj0, then DFSEs of leaders can be modified as

5. Second layer - distributed affine formation control for followers

In this section, we would tackle the distributed affine formation problem of the followers in the second layer. A similar DFSE protocol is proposed to estimate the weighted average of the leaders’ velocity and position information in the finite time. Then, the distributed affine formation control law by state feedback with collision avoidance is designed for the followers.

We propose the following DFSE protocol for the followers i ∈Vf

where β3,β4are positive constants,diis a nonzero constant,^qi,^viare the estimations of the weighted average of the leaders’positions and velocities for each follower respectively. It should be noted that ^qi=qi, ^vi= ˙qifor i ∈Vf, and the weighted average of the leaders’ positions for the ith follower is denoted as cifor i ∈Vf. Then, we define

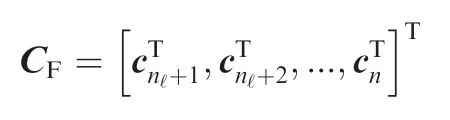
Then a theorem is given as below,which gives the feasibility of the proposed DFSE algorithm. To prove this theorem, a lemma is needed45

From Theorem 4, the accelerations of the leaders are bounded. Then, we define a positive constant δFfor the ith leader with i ∈Vℓ, which satisfies

Theorem 5. There exist two positive constants β3and β4. If Assumptions 1-4 hold,with Eqs.(60)and(61),the followers can achieve the accurate estimations of the weighted average of the leaders’ positions and velocities for the corresponding ith follower denoted as ciand ˙ciin the finite time respectively,which leads to

Proof. Under Assumptions 3-4 such thatsatisfies nonsingularity, there exists a permutation matrix T such that all of the leading principal minors ofare nonzero. According to Lemma 5, it can be obtained to find a diagonal matrix D′to place all the eigenvalues ofin the right-half plane.The permutation matrix T has the proposition of T-1=TT, thus.From both sides of this equation,

where D=diag（di），i ∈V.

Here, with Assumptions 3 and 4 we can give the relation between FLand CFas

Then, we can acquire two finite time periods

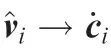
Consider the case t ≥T4, we define the generalized tracking errors as

where the virtual control

with Ξiand Vaidefined the same as above,and there exists a positive constant k2i.By importing the adaptive NNs similarly to the first layer,we can obtain the compensated models of the followers i ∈Vfas

We further develop the following distributed affine formation control protocol and the adaptive law for the followers in the second layer as

where Kiis the control gain matrix, γiand θiare the positive constants, ^Wi，kis the kth column vector of ^Wi, and z2i，kis the kth entry of the vector z2i.

Proof. Similar to proof of Theorem 4, by constructing the following Lyapunov function candidate for i ∈Vf

Differentiating V6irespect to the time, one has

According to Property 1, Eq. (39), as well as Eqs. (75) and(76), then Eq. (81) can be reorganized as

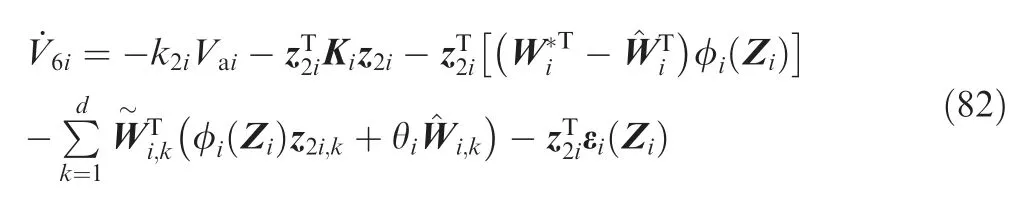
In the sequel, with the same inequalities as Eqs. (51) and(52), the inequality of ˙V6ican be expressed as

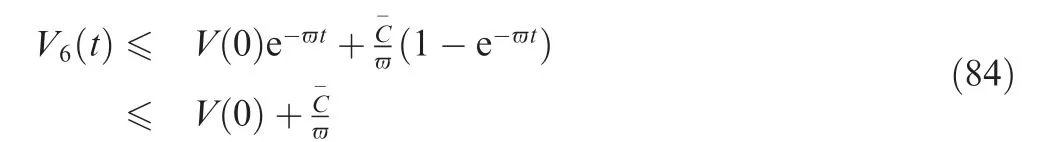
where, and z1can keep inside the compact set Ωz1.Then,compact sets for z2andcan be obtained following the similar procedure. Here concludes the proof of Theorem 6.

Remark 5. In this paper, we assume that the proposed twolayer control scheme is with velocity measurement.In practice,velocity sensors might not be equipped on the spacecraft to save cost and space. Under the circumstances, the output feedback control protocol based on the high-gain observer can be adopted,which has been described in detail in our previous work.24

6. Numerical simulation

In this section, according to different requirements of formation types, corresponding simulations are studied to verify the feasibility of theoretical results.

We design a nominal formation （G，qr） of 7 spacecraft together with the configuration matrix Q（ qr） in R2as demonstrated in Fig. 3. The leaders are labelled 1, 2, 3 in the first layer, and the followers are labelled 4, 5, 6, 7 in the second layer. The leader number satisfies 3=d+1 and the directed interaction graph G is 3-rooted. The obtained hybrid Laplacian matrixis provide d as below, where the rank of signed Laplacian matrix Lsmeets 4. Then, we are able to calculate the corresponding stabilizing matrix D=diag（1，1，1，1，1，-1，-1） by Algorithm 1 in Ref. 42.

The spacecraft team moves on the 7136 km near-circular orbit, and the corresponding simulation length unit is meter. The initial position of virtual agent 0 is q0（0 ）= ［0 ，0］T, the initial positions of three leaders are q1（0 ）= ［25，0］T，q2（0 ）= ［15，15］T，q3（0 ）= ［10，-15］Tand four followersareq4（0 ）= ［0，-30］T， q5（ 0）= ［0，30］T，q6（0 ）= ［0，-15］T，q7（0 ）= ［0，15］T, meanwhile all the initial velocities are zero. The control parameters are β1=β2=β3=β4=5， Ki=0.1I2and k1i=k2i=5. The parametersfortheNNsaresetas μr=random［-1，1］， ηr=10 and W^i（0 ）=0. The triangle formation of spacecraft tracks sinuous trajectories of the moving target with red circle as Fig. 4, and the time-varying radius‖hi0‖2of this formation is set as 20+20sin（0.005t）. Two obstacles are placed at the points qo1= ［200，25］Tand qo2= ［200，-25］T, with the radius ro=20 marked with cyan and the minimum safe distance dsafe=10 colored with black.In addition, the inter-agent danger range rdangeris set as 5,and the rest parameters of simulation are adopted from Table II in our previous work24and omitted here due to the page limit.

Fig.3 Triangle nominal formation of 7 spacecraft and corresponding configuration matrix.

Fig.4 Time-varying trajectories of triangle spacecraft formation.

Fig.5 Tracking errors of leaders and followers in two-dimensional plane.

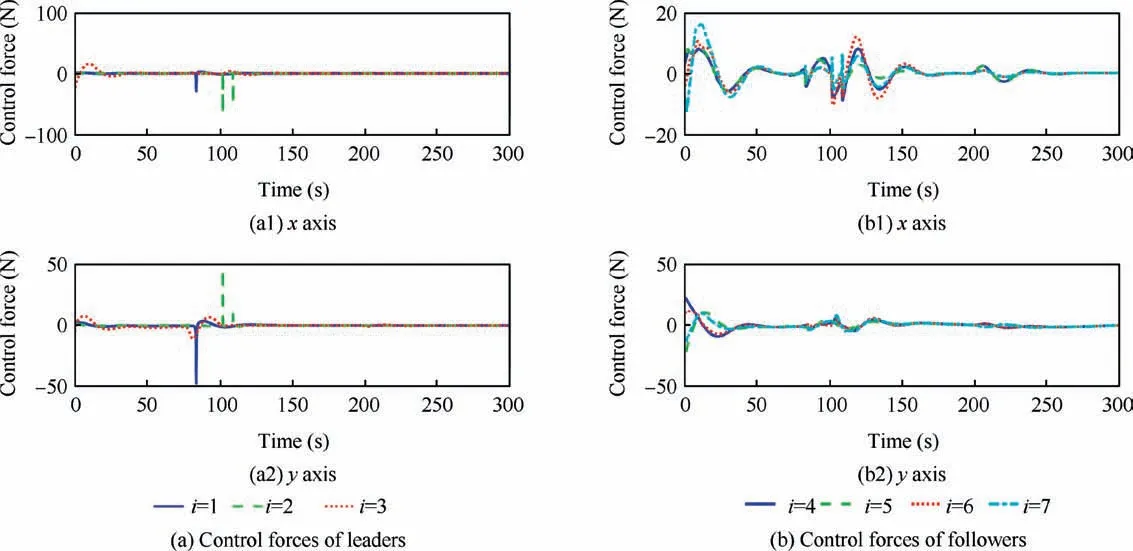
Fig.6 Control forces of leaders and followers in two-dimensional plane.

Fig.7 The norm of NN weights‖ of leader 1 and‖ of follower 4.

Fig.8 Minimum distance between spacecraft.

Fig.9 Hexagon nominal formation of 10 spacecraft.

From Fig.4,we can see that all the spacecraft quickly converge into and synchronously enclose the dynamic target from the randomly selected initial positions,where two obstacles are successfully avoided. The tracking errors of leaders in the first layer and followers in the second layer are shown in Figs.5(a)and 5(b), respectively. The large tracking errors occur due to more control efforts needed to avoid the obstacles and reconfigure the formation as Fig.6,especially larger at both ends of passing the narrow gap between two obstacles. Fig. 7 shows the norm of NN weights, i.e.,of leader 1 andof follower 4. As shown in Fig. 8, the minimum distance between neighboring spacecraft does violate the required distance in the whole flying process.In the sequel,we carry out the hexagon formation test, in the formation configuration there exit more spacecraft and a complex interaction graph as Fig.9.Corresponding trajectories of spacecraft for tracking the dynamic target are demonstrated in Fig. 10. It should be noted that the target may be outside the smaller formation while approaching the obstacle,but it quickly returns after finishing the avoiding maneuver. The results show that the proposed two-layer control scheme has good tracking performance and collision avoidance capability.

Remark 6. The adopted spacecraft model is created in threedimensional (3D) space, to apply our approaches, the vertical coordinates of all the spacecraft are fixed as the same value throughout the simulation process.It implies that the obtained results are all projected into a plane. In this way, the simulations are the same as that being carried out in the 2D plane.

7. Conclusions

In this paper, the two-layer target-enclosing affine formation control schemes with collision avoidance are proposed for uncertain EL spacecraft models. By adopting the superiority of affine transformation, multi-layer time-varying encirclements surrounding a dynamic target can be realized.Directed graphical DFSEs are used to estimate the desired positions and velocities for the spacecraft in both layers respectively,and these DFSEs, designed separately, can improve the designing flexibility of the formation controllers. Additionally, NNs are used to approximate model uncertainties to improve the system performance. The artificial potential functions are integrated into backstepping controllers to dodge inter-agent and pop-up obstacle collisions. In future work, we will extend our approach to practical situations,such as control with communication delays or state constraints.

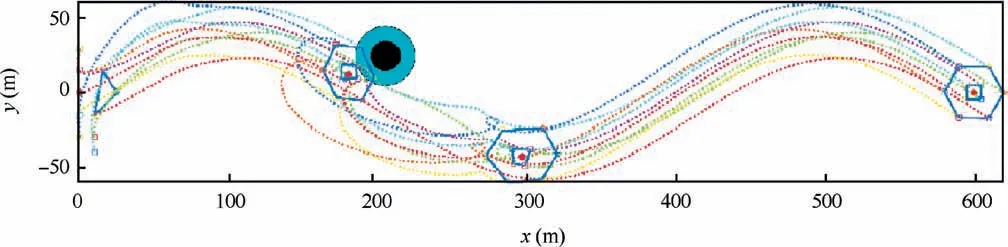
Fig.10 Time-varying trajectories of hexagon spacecraft formation.

Acknowledgement

The authors would like to thank Prof. Shiyu ZHAO at the University of Sheffield and Prof. Ben M. CHEN and Prof.Sam S. GE at the National University of Singapore for the inspiration and discussion of the idea presented in this paper.This research was sponsored by National Natural Science Foundation of China (Nos. 61673327, 51606161, 11602209,91441128), Natural Science Foundation of Fujian Province of China (No. 2016J06011), and China Scholarship Council(No. 201606310153).