基础参数优化的柴油机调速系统自适应控制

孙 宁 游 宇 曹雪梅

（河南科技大学机电工程学院，河南 洛阳471000）

驱动螺旋桨的船舶主柴油机在船舶行驶过程中需要在工况变化时快速准确地转换各工况 （如经济功率工况、动力功率工况）要求的核定转速，在同一工况下则要求柴油机能及时地调整与变化负荷相匹配的喷油量， 保证柴油机在核定的转速下稳定高效运行， 因此柴油机调速控制系统必须满足响应速度快、调控精度高、抗干扰能力强的要求。 PID 控制算法具有易于工程实现、鲁棒性强的特点，已经应用于柴油机调速控制系统[1]。 但传统的PID 控制器参数为离线整定， 对动态工况的适应性有待增强。 为此学者们提出了多种改进控制算法以改善其性能[2-4]。 柴油机调速控制系统为嵌入式控制系统， 其主控芯片的计算和存储能力有限， 因此需要选择适用于嵌入式控制系统的控制算法。

模糊PID 控制可实现在线修正控制器参数，较好地提高柴油机调速系统的动态性能，并且对系统计算能力要求不高，适用于船舶柴油机控制系统[5]，但对模糊PID 稳态误差的消除能力不强,其控制效果取决于PID 控制器参数初值和模糊修正规则的合理设置。

PID 控制器参数传统工程整定方法有Ziegler-Nichols 整定法、临界比例度法、衰减曲线法等[6]，这些方法虽然可实现PID 控制效果但无法提供最优值，且比例、积分和微分环节并非各自独立，而是相互关联和互相补偿，因此以比例系数Kp、积分系数Ki和微分系数Kd这三个参数为自变量的性能指标可以在多个可行解区域实现，并存在多个局部最优解。 模糊修正虽然能对控制器参数在线修正， 对控制过程进行优化，但其修正的结果受初始设置的基础值限制，只能逼近初始值所在可行解区域的局部最优。 为取得调速控制系统最优化的控制效果，本文提出基于遗传算法优化控制器初始参数的模糊PID 算法。

1.柴油机调速系统数学模型

柴油机调速系统的调速原理为当外界负载变化时，柴油机调速控制器计算出喷油泵齿条位移的变化量，并通过执行机构推动喷油泵齿条从而改变每循环喷油量的大小，使得柴油机转速保持恒定。

柴油机结构复杂，工作过程涉及诸多物理化学过程，运行机理复杂，建立过于复杂的数学模型也未必适用和准确，一般可以用纯滞后的一阶惯性环节建立柴油机的简化数学模型[7]。 当柴油机的输出力矩与作用在曲轴上的负荷力矩平衡时（忽略机组摩擦力矩），柴油机输出恒定转速，柴油机输出力矩与负荷力矩的差值引起曲轴角速度变化：

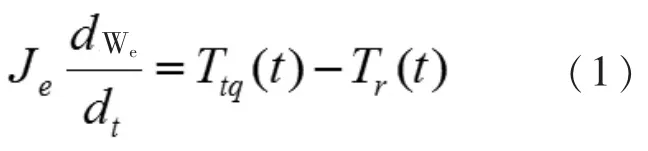
式中：Je为柴油机及机组转化到曲轴上的转动惯量，we为曲轴角速度，Ttq为柴油机输出力矩，Tr为负荷力矩，t 为时间变量。

柴油机输出力矩Ttq由循环供油量决定，不考虑实际工作中柴油机因惯性和间断性造成的滞后环节，Ttq与齿条位置Y 的关系可简化为比例环节表示，其增益常数Ky为

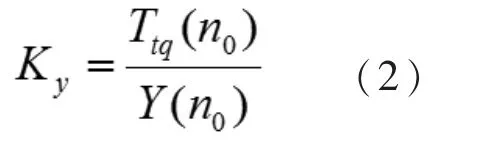
设订，式中：no为柴油机额定转速。

由式1 和式2 可推导出，柴油机输出转速ne与齿条位置Y 的传递函数为

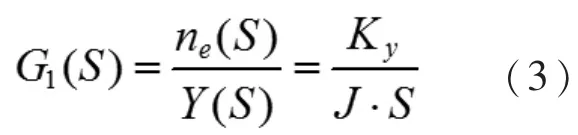
式中：S 为复变量；G 为传统函数。

因容积惯性、热惯性和发火间断等因素的影响，柴油机输出转矩变化时间滞后于柴油机喷油泵供油齿条位置改变的时间，此纯滞后环节的传递函数为

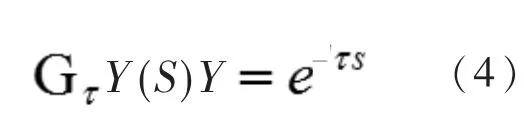
柴油机电子油门执行机构为电液伺服机构。执行机构为一阶惯性环节，齿条位置Y 与控制器输出电流Ie的传递函数为

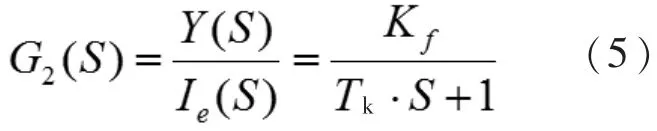
式中，Ie为控制器输出电流，Kf为脉宽调制放大器电流放大系数，Tk为与执行机构结构相关的常数。

由式(3)、(4)和(5)得到柴油机调速系统的数学模型为纯滞后的二阶系统，其传递函数为

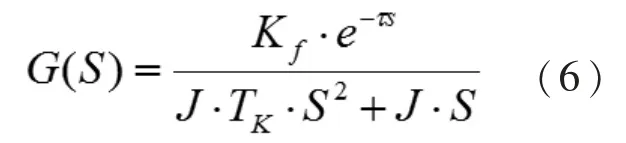
2.船舶主柴油机调速系统自适应控制器结构及控制算法

2.1 船舶主柴油机调速系统自适应控制器结构

基于PID 控制器基础参数优化的船舶主柴油机调速系统自适应控制器结构如图1 所示。

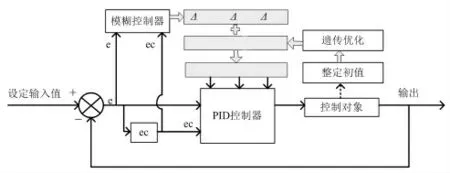
图1 船舶主柴油机调速系统自适应控制器结构

自适应控制器以PID 控制器为核心，以设定转速值和实际转速值之差e 以及其差值变化率ec（即两个采样点间误差变化量）为输入。 PID 控制器的比例、微分、积分 参数Kp、Ki、Kd是由初始值Kp0、Ki0、Kd0与修正量△Kp、△Ki、△Kd共同决定的。 初始值由遗传算法优化得出，修正量由模糊控制器提供。

2.2 PID 控制算法

PID 控制器是一种比例、积分、微分并联控制器。 离散化的增量式PID 控制器输出u 可表示为

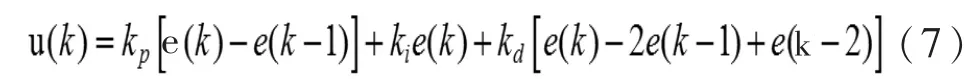
2.3 基于遗传算法的PID 控制器参数优化整定

遗传算法(Genetic Algorithms GA)是将生物进化过程中适者生存规则、群体内部染色体的随机信息交换机制、染色体变异机制相结合的在问题解空间内全局并行随机搜索优化算法[7]。 该算法的原理为首先在问题解空间内随机产生多个初始解个体，构成初始种群，然后以初始解个体的适应度为判据，根据适者生存原则选择适应度的个体进行交叉、变异，从而产生新一代更加接近优化目标的染色体（初始解个体）种群，经过多代不断地淘汰、进化、变异，最后求得优化目标的最优解。 算法包括初始种群设置、参数解码、计算适应度、选择、交叉、变异等计算步骤，算法本身已经比较成熟。 有别于已经知目标函数和问题解空间的遗传优化计算，PID 参数优化解与搜索空间和适应度函数的设置相关。

问题解空间搜索范围的求法为： 用Z—N 整定法[8]求解初值Kp1、Ki1、Kd1，并以此初值为中心向两边适度延拓，这样的优点在于可以充分利用工程整定法的合理内核， 从而缩小了搜索空间。设K 为Z—N 法整定值，λ1，λ2为延拓系数，则可得Kp0、Ki0、Kd0的取值区间为

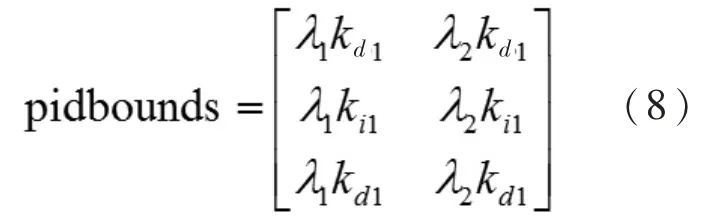
以比例参数的染色体为例，把二进制的单个染色体转化为一个十进制，问题解空间内十进制解Xkp的计算公式为

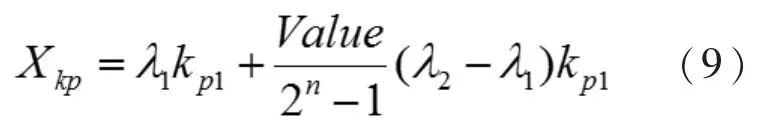
式中，Value 为二进制的单个染色体值所对应的十进制数值。

适应度函数表明个体对算法的优化目标适应能力需依据控制系统的优化目标来构造。 以绝对误差积分来衡量控制效果[9]，定义适应度函数为绝对误差积分的倒数，则其最优解对应的控制效果为系统响应速度快、抗扰动能力强但存在微小稳态误差；以二次型性能指标函数来衡量控制效果，其优化解对应的系统响应速度落后于绝对误差积分，但有利于消除稳态误差。 船舶主柴油机对稳态性能和抗扰动能力都有较高要求，因此定义适应度函数f 为二次型性能指标函数Se的倒数，Se为

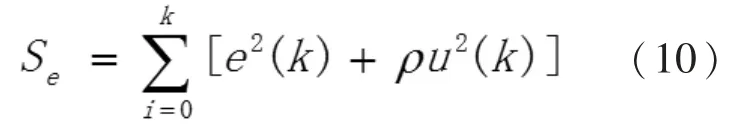
式中：ρ 为控制器输出的权重系数，ρ∈[0,1]；K 为采样序号；u 为增量式PID 控制器输出，e 为转速偏差。

2.4 模糊PID 自整定算法

模糊自整定PID 以误差e 和误差的变化率ec 为输入，PID 控制器根据模糊规则在线实时地输出PID 参数的修正值△Kp、△Ki、△Kd作为输出变量。

根据参数Kp、Ki、Kd在系统输出特性中的影响情况制定模糊规则：当e 较大的时侯，应加大Kp以提高响应速度，同时为避免微分和积分过饱和，应减小Kd和Ki值。 当e 和ec 为中等大小的时候，为减小系统响应的超调量同时又保证一定的响应速度， 应适当减小Kp、Kd值。 当e 较小的时候，为了使系统具有较好的稳态性能，应增大Ki的值， 为了避免系统振荡提高抗干扰能力，当ec 较小时，增大Kd；当ec 较大时，减小Kd。

以Kp为例，其计算公式为

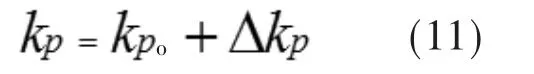
△Kp的模糊控制规则见表1。

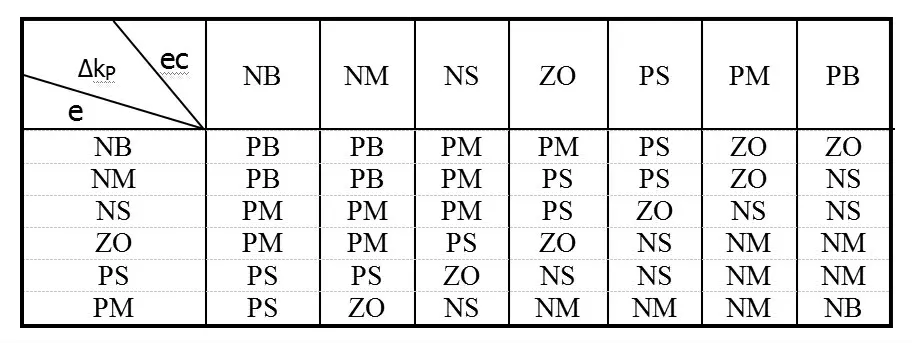
表1 比例系数修正量模糊控制规则

3.算例仿真验证

柴油机调速系统的传递函数为

仿真时间5 秒，步长0.01 秒，在2 秒时加入10%的负载扰动， 编制MATLAB 程序求柴油机输入转速从1500r/min 转换为1600r/min 时的阶跃响应。图2、3为初始参数由Ziegler-Nichols 法整定的模糊PID 和初始参数遗传算法最优化的模糊PID 响应曲线。

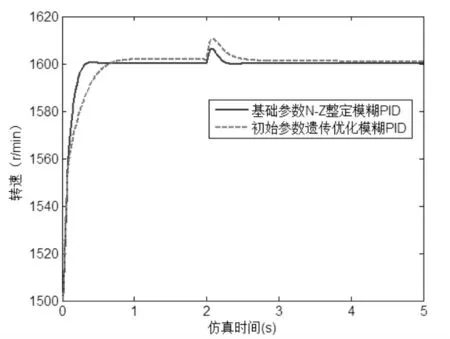
图2 两种对比算法的阶跃响应曲线

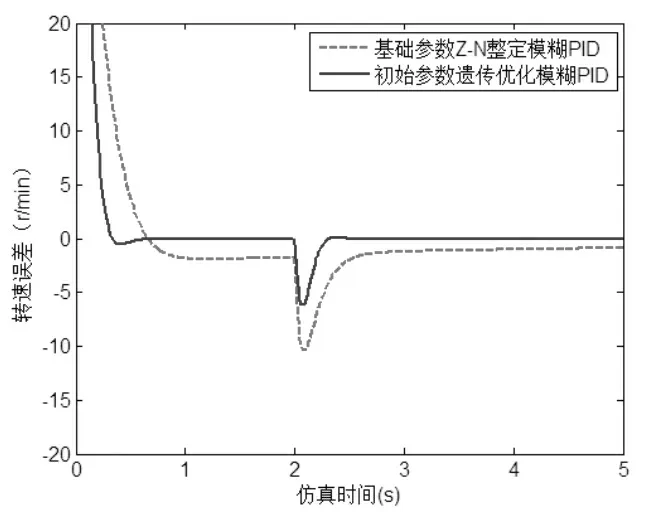
图3 两种对比算法的误差曲线

从图2 和3 中可以看出，在初始基础参数遗传算法最优化的模糊PID 控制作用下，调速系统响应速度快，有少量在许可范围内的超调，在受到扰动的情况下，误差峰值为-5，误差持续时间为0.2 秒。 因优化过程中选用二次型性能指标函数，基础参数遗传算法最优化的模糊PID 控制算法的系统稳态误差为0。 初始基础参数Z—N 整定的模糊PID 控制算法作用下， 调速系统无超调，但响应时间、扰动误差持续时间和误差峰值大于本文优化算法， 并且无法完全消除稳态误差。

本文提出基础参数优化的自适应控制算法，通过离线工程整定确定问题解空间搜索范围，再经遗传算法求得最优比例、积分、微分参数作为模糊PID 控制器的基础参数，用二维模糊控制器根据系统实时状态输出比例、积分、微分参数的修正值修正基础参数，实现根据工况实时输出控制器参数。 这种算法的遗传优化为离线整定，不占用控制系统资源，采用这种控制算法的柴油机调速响应速度、抗干扰能力和稳态误差明显优于对比算法，可最优满足柴油机调速控制系统反应灵敏、调控精度高、抗干扰能力强的要求。