统计与概率扩大“朋友圈”

■广西来宾高级中学 覃尚猷 杨 佶 胡利洁

在大数据时代，科学技术飞速发展，随着高中数学课程不断改革，“统计与概率”既是高中阶段数学课程的主线，又是大学数学教育的基础课程，成了高考出题的新亮点，特别是2019年全国Ⅰ卷将“统计与概率”题放在第21题，让人刮目相看。近年来，有不少的统计与概率题注重情境生活化、素材新颖化、问题实用化，同学们分析问题与解决问题的能力不断提升才能解决“朋友圈”不断扩大的统计与概率问题，下面选取几道题与大家共同赏析。

一、概率与数列交汇

例1为了治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验。试验方案如下：每一轮选取两只白鼠对药效进行对比试验。对于两只白鼠，随机选一只施以甲药，另一只施以乙药。一轮的治疗结果得出后，再安排下一轮试验。当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效。为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0 分。甲、乙两种药的治愈率分别记为α 和β，一轮试验中甲药的得分记为X。

(1)求X 的分布列；

(2)若甲药、乙药在试验开始时都赋予4分，pi(i=0，1，…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1，2，…，7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1)。假设α=0.5，β=0.8。

①证明：{pi+1-pi}(i=0，1，2，…，7)为等比数列；

②求p4，并根据p4的值解释这种试验方案的合理。

解析：(1)由题意可知X 的所有可能取值为-1，0，1，所以P(X=-1)=(1-α)β，P(X=0)=αβ+(1-α)(1-β)，P(X=1)=α(1-β)。

所以X 的分布列为表1：

(2)因为α=0.5，β=0.8，所以a=0.5×0.8=0.4，b=0.5×0.8+0.5×0.2=0.5，c=0.5×0.2=0.1。

①因为pi=api-1+bpi+cpi+1(i=1，2，…，7)，即pi=0.4pi-1+0.5pi+0.1pi+1(i=1，2，…，7)，整理可得5pi=4pi-1+pi+1(i=1，2，…，7)，所以pi+1-pi=4(pi-pi-1)(i=1，2，…，7)。

所以{pi+1-pi}(i=0，1，2，…，7)是以p1-p0为首项，4为公比的等比数列。

②由①知pi+1-pi=(p1-p0)·4i=p1·4i，所以p8-p7=p1·47，p7-p6=p1·46，…，p1-p0=p1·40。

以上各式相加可得p8-p0=p1·(40+41+…+47)

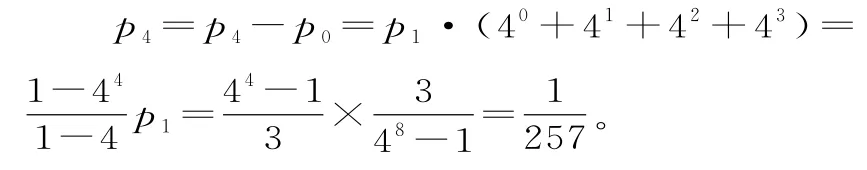
p4表示最终认为甲药是更有效的。由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8时，认为甲药更有效的概率为≈0.003 9，此时得出错误结论的概率非常小，说明这种实验方案合理。

点评：本题考查离散型随机变量分布列的求解、等比数列的证明、求数列通项公式和数列中的项的问题。本题是在概率与数列知识交汇处出题，具有较强的综合性，对同学们分析和解决问题的能力有较高要求。要过三关：(1)阅读关；(2)数列关；(3)概率运算关。

二、概率与立体几何交叉

例2设ξ 为随机变量。从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ 的值为两条棱之间的距离；当两条棱异面时，ξ=1。

(1)求概率P(ξ=0)；

(2)求ξ 的分布列，并求其数学期望E(ξ)。

解析：(1)若两条棱相交，则交点必为正方体8个顶点中的1个，过任意1个顶点恰有3 条棱，所以共有对相交棱，因此

所以随机变量ξ 的分布列为表2：

表2

点评：本题在立体几何知识的环境下考查概率、分布列、数学期望，是概率、立体几何、组合等知识的综合，能否“翻译”成概率知识成为关键。要过三关：(1)立体几何关；(2)概率关；(3)排列组合运算关。

三、概率与面积相伴

例3设A，B，C，D，E，F为单位圆上的六等分点。现任选其中三个不同点构成一个三角形，记该三角形的面积为随机变量S。

(2)求S 的分布列及数学期望E(S)。

解析：(1)从六个点中任选三个不同点构成一个三角形共有种不同选法，其中S=的是有一个角为30°的直角三角形，共6×2=12(种)，所以

(2)S 的所有可能取值

结合(1)知S 的分布列为表3：

表3

点评：本题考查概率、离散型随机变量的分布列及数学期望的求法，是概率与面积、组合等相关知识的综合题，难度不是很大，解题时要认真审题，其中“翻译成“有一个角是30°的直角三角形”是解题的关键，画出图形有助于问题的解决，注意排列组合知识的运用。要过三关：(1)理解“翻译”关；(2)平面几何关；(3)概率、排列组合运算关。

观察近几年高考题中的统计概率题，具有情境新、素材新、题型新等特点，与数列交汇，同立体几何交叉，与面积相伴，“朋友圈”不断扩大，在统计概率不断招兵买马扩大队伍的同时，对同学们综合解题能力的要求不断提升，需要在题目特定的情境下冷静分析题目，学会将复杂的题意简单地“翻译”出来，再用概率的知识解决。