用时域分析法求解冲激响应的方法

汪 建

(华中科技大学电气与电子工程学院，湖北武汉430074)

0引 言

在“电路原理”课程暂态分析教学中，冲激响应的求解是一个重点内容，也是难点之一。当采用时域分析法时，冲激响应的求解通常可应用下述三种方法［1-3]:①由阶跃响应求解，即阶跃响应对时间变量的导数为冲激响应;②将冲激响应化为零输入响应求解，即先求出冲激激励所建立的电路初始状态uC(0+)和iL(0+)，再求零输入响应便获得冲激响应。③还可用比较系数法，即通过比较描述冲激响应的微分方程两边奇异函数的系数来求得冲激响应。

但当电路中含有电流源—电感割集、电压源—电容回路或电压源—电感回路、电流源—电感回路时，应用上述某种方法求解时可能会遇到困难。本文通过一些较典型例题的分析来说明这些方法的运用，用以帮助学生建立正确思维方式，增强其灵活运用所学概念和方法分析电路问题的能力，提高讲解冲激响应求解方法的教学效果。

1 由阶跃响应求冲激响应

电路中某一变量的阶跃响应通常用S(t)表示，冲激响应用h(t)表示。冲激响应和阶跃响应的关系是h(t)=dS(t)/dt。

［例1] 求图1所示电路的冲激响应uC(t)。

图1 例1电路

解:先求电路阶跃响应。令电源电压为ε(t)，uC(0－)=0。一阶电路可用三要素法求解

则阶跃响应为

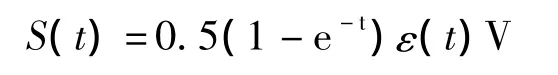
于是，所求冲激响应为

2 将冲激响应化为零输入响应求解

冲激电源的作用可视为在其施加于电路时建立初始状态，即使uC(t)和iL在t=0时发生跳变。冲激电源在t=0时作用于电路，在t＞0后冲激电源的输出为零，则电路的响应可视为由冲激电源所建立的初始状态引起的零输入响应。

对于冲激电源所建立的电路初始状态uC(0+)和iL(0+)可用两种方法求得:①由冲激电源作用时(0－～0+)的等效电路求出通过电容的电流iC(t)和电感的端电压uL(t)，再由两种动态元件的伏安关系式求得uC(0+)和iL(0－)。因uC(0－)及iL(0－)=0，则在冲激电源作用时，电容等效于短路，电感等效于开路;②由电路的微分方程求出。

［例2] 电路仍如图1所示。试用化为零输入响应求解的方法求其冲激响应uC(t)。

解:先求冲激电源所建立的初始状态uC(0+)。在冲激电源作用时，电容相当于短路，作出等效电路如图2(a)所示，求得iC(t)=δ(t)/3+2i(t)，于是有

我们可建立电路的微分方程再求出uC(0+)。对图2(b)所示电路，依据KCL和KVL可建立电路的微分方程为

对方程两边同时从0－～0+积分，可求得

t＞0后的电路为零输入电路，如图2(c)所示。其中uC(0+)=0.5V，τ=1s。于是电路的冲激响应为

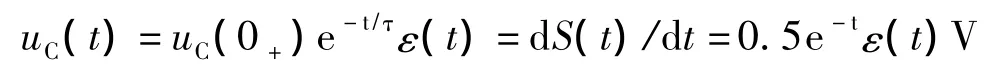
图2 例2计算用图

［例3] 如图3(a)所示电路中，已知:L1=1H，L2=0.5H，R=1Ω，试求冲激响应i1(t)和i2(t)。

解:此题若用第一种方法先求阶跃响应，再求冲激响应的方法，会遇到困难。原因是此电路中有一电压源—电感回路，当阶跃电源作用，用三要素法求稳态值时，两个电感相当于短路将电源短接而无法求出电感电流的稳态值。这里采用化为零输入响应的方法进行求解。作出δ(t)作用(t=0)时的等效电路如图2(b)所示，可得

u1(t)=δ(t)，u2(t)=0

于是求出初始状态为

t＞0后为零输入电路，如图3(c)所示。因该电路有两个电感并联，在动态过程结束后，两电感中的电流均不为零。

图3 例3计算用图

为此先求响应u(t)，有

其中，i(0+)=i1(0+)－i2(0+)=i1(0+)=1A，τ=Leq/R=(L1//L2)/R=1/3s，于是有

则求得冲激响应为

3 比较系数法求冲激响应

一个n阶网络的微分方程，其一般形式为

若x(t)=δ(t)且电路的原始状态为零状态，则响应y(t)为冲激响应。

根据微分方程的具体形式，冲激响应h(t)的表达式可分为两种情况。

1)若n＞m，则h(t)中不含有冲激函数及其各阶导数，其一般表达式为

式中，yh(t)是齐次微分方程的解。

在确定了h(t)表达式的形式后，将其代入到微分方程中进行系数比较，从而获得冲激响应。

［例4] 某电路的微分方程为dy(t)/dt+4y(t)=2d2x(t)/dt2+3x(t)，试求该电路冲激响应h(t)。

解:由于n=1，m=2，故由式(3)得冲激响应的表达式为

而dh(t)/dt=-4e－4tε(t)+Kδ(t)+K0δ'(t)+K1δn(t)

将dh(t)/dt和h(t)代入原微分方程，可得

比较等式两边各项系数，解得

则所求冲激响应为

［例5] 用比较系数法求图1所示电路的冲激响应。

解:列出该电路的微分方程为

因n＞m，且该微分方程的齐次解形式为ke－t，

则由(2)式，知冲激响应的表达式为

将上式代入微分方程后进行系数比较，可求得k=0.5，则所求冲激响应为

［例6] 电路如图4所示，试求其冲激响应i(t)。

图4 例6电路

解:此电路的求解若用第二种方法化为零输入响应的方法会遇到困难，原因是电路中存在电流源-电感割集。当冲激电源作用时，两个电感相当于开路而难以求出此时两个电感两端的电压因而不能求得冲激电源所建立的初始状态。为此用比较系数法求解。对图4所示电路右边回路列写KVL方程，有

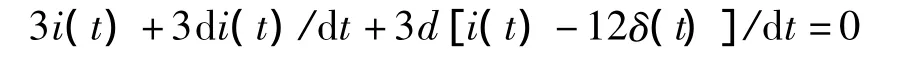
整理后得到电路的微分方程为

因n=m，由式(3)知响应的表达式为

将上式代入微分方程，经系数比较，可得K=－3，K0=6。

则所求冲激响应为

4 结语

本文用一些较典型的例子从教学的角度讨论说明了在时域中求解冲激响应的方法，以提高这一内容的教学效果，帮助学生正确地理解和掌握冲激响应的概念，特别是冲激响应的各种求解方法。由此达到开拓思路和正确地运用所学知识分析各种电路问题的能力。

［1] 邱关源，罗先觉.电路(第五版)［M] .北京:高等教育出版社，2006

［2] 周守昌主编.电路原理［M] .北京:高等教育出版社，2004

［3] 李翰逊主编.电路分析基础(第三版)［M] .北京:高等教育出版社，1993