探索多层问题，透析数学模型

杨薇

摘要：在现今的小学数学应试教育中，解应用题或叫解决问题是不少学生的薄弱环节。解应用题的本质就是数学建模，而建模的关键环节是对问题模型的建造，相当于应用题的数量关系模型的确立。本文以四年级数学广角中鸡兔同笼典型问题作为案例，探索以建立数学模型为主的课堂。

关键词：数学建模;数量关系;鸡兔同笼;应用题

学生错解应用题，离不开一些主要原因。例如，学生对题目文字、词语的意思把握不足、生活视野狭窄和缺乏思维想象导致无法审题或审题偏差，分析问题时难以准确提取数量关系。课堂上没有完全理解问题的数量关系，知其然而不知其所以然，靠发挥记忆力来推敲类似题目的数量关系。

有些教师会以不同的数量关系划分成不同类型的应用题针对性地进行大量训练，这样很容易把题目“讲死”，学生思维固化，以记忆解题方法为主，不利于思维发展。

一、解应用题的本质——数学建模

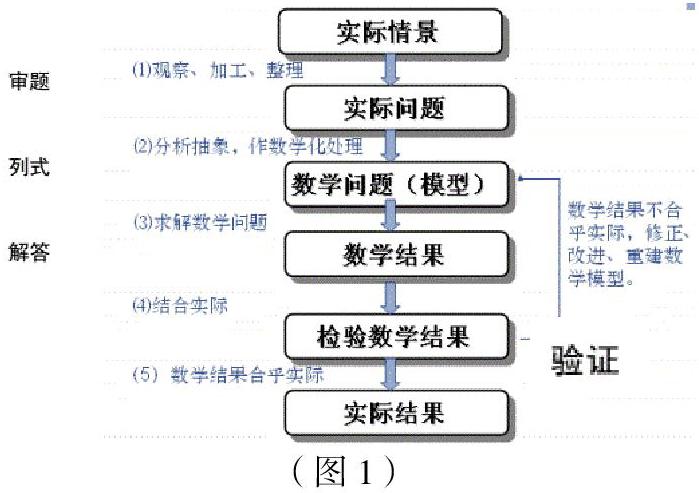
这是某些专家画出的数学建模流程图（如图1），这过程跟解应用题非常相似，实际上就是小学生解应用题时的步骤：审题、分析数量关系、列式计算或列方程解答、验证。而建模中的“数学问题（模型）”这个关键环节跟应用题中数量关系的分析和确立，都是用一些文字、符号或图形表达这个关系而形成的模型，其本质没有区别。所以进一步研究怎样把数学建模思想融合到解决问题里去，对提高学生解决问题的能力有一定的研究价值。

不管是何种因素导致学生解题能力低下，也应归咎于学生和教师对问题的数量关系理解不深刻。解应用题时，有正确完整的数量关系模型才可以解答问题，不论是列算式还是列方程。因此，重视数量关系的分析、提取和运用是提高学生应用题解题能力的核心。

二、探索利用建模思想解决问题的课堂案例

在小学数学应用题范畴里，用特定的数量关系或特殊步驟解决问题，我们把这种类型题目叫做典型应用题，因其有较大的研究价值，我们把这些应用题归类成各种“问题”。下面以四年级下学期的“鸡兔同笼”问题作为案例来解析建立数学模型教学方法。

课上，教师引入一类型问题“笼子里有若干只鸡和兔，从上面数，有8个头，从下面数，有26只脚。鸡和兔各有多少只？”基于建模的一般步骤，我把探索这一问题的课堂实践分成几个必要环节展开：分析问题、构建模型、验证模型。

1、分析问题

高等数学里的数学建模的第一步是对象属性的分析和背景调查，而小学数学里面，解题第一步是审题，这里可以理解成后者是前者的初级版。审题时除了读出隐藏信息（例：兔有4脚，鸡有2脚），还需要初步感知条件与问题之间的关联性（例：只有知其中一个只数能求另一个只数，只数与脚数有关，怎样通过脚数来确定只数是关键）。对于“鸡兔同笼”问题学生主要通过画图、枚举甚至利用表格有序列举等方法去分析（如图2、3），因此教师应鼓励并给予充分时间组织学生动手试探，经历这个过程充分感知后，教师引导指出：不管用什么方法，实际解题方法都离不开“假设”。有人一次假设就碰对，有些则假设多次，并引导学生往有没有更方便快捷的方法来解决这种问题的方向思考。

这里的分析问题环节，不是单纯地思考分析，简单来说是通过动手来思考分析，不断累积这种基于数形结合的动手操作的经验来构建想象。这里，画图法是最好的体现。同时让学生感受到当数据变大时，粗糙的假设方法是行不通的，需要产生一种相对固定的解决办法，也就必须找到固定的数量关系来建立模型。

2、构建模型

（1）从假设中感知规律

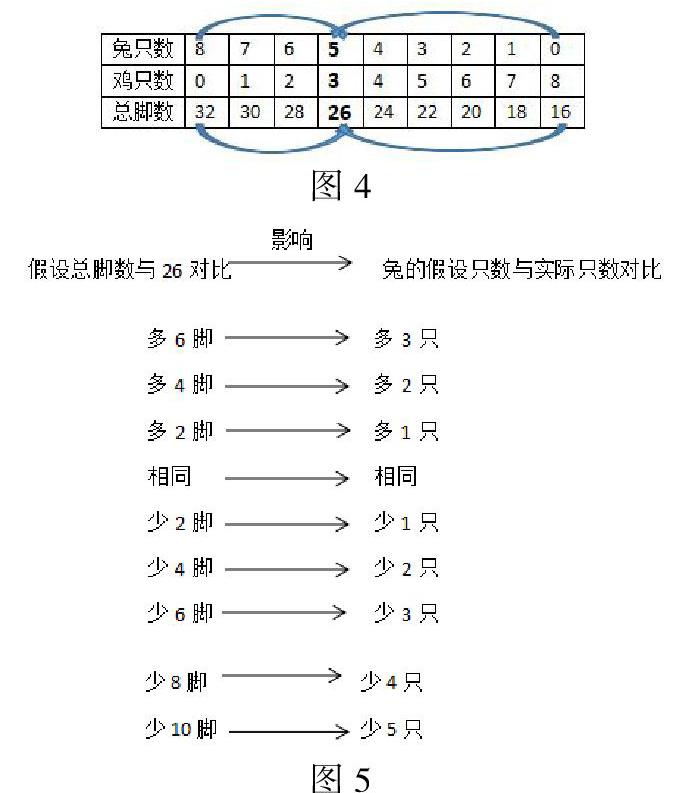
在充分体验假设后，教师根据实际情况可设问“在这个过程里说说你的发现”。学生不管是哪种假设，当他们直观感受到当假设得到的总脚数比26（实际总脚数）多时，说明假设兔的头数多了，反之。教师接着引导指出：假设总脚数与26的差值与兔多出的只数有关。然后进一步观察列表（如图4）中数据探索这种关系（如图5）。

学生不难发现，每多一只兔，总脚数就多2;也就是总脚数多了2n，兔假设只数多n，反之。所以不管任何一种假设，只要知道与实际脚数相差多少，就能推出兔的假设只数比实际相差多少，我们可以利用这个关系来确定兔的实际只数，从而确定鸡只数。

（2）提取算式，初构模型

在基于学生不同的假设上，老师顺势引导学生列算式表达出不同的假设，尝试在这些不同的“假设”算式里找到模型的影子。

例：当鸡只有0只，那么兔就有8只：………假设的脚数比实际多

总脚数比实际多6，那么兔的假设只数多了，说明兔实际有，鸡有。如此类推。

………………

不管学生如何假设兔只数和鸡只数，都有能通过鸡与兔的总脚数和实际总脚数的差值除以“2”来求出多了几只兔或少了几只兔，从而对应求出鸡兔的实际只数。

（3）深入参与模型建构，发掘模型本质

上一个例题是以动物鸡和兔为情景，为了更接近鸡兔同笼问题的本质，我们可以对上一个例题的对象和情景稍作更改，以达到变式效果。可举出第二例题：停车场里有10个停车位，里面停满了三轮车和摩托车，每个停车位只能停一辆车，如果这里所有车一共有23个轮子，问三轮车和摩托车各有多少辆？

学生基于第一例题的探究经验，不难看出“10个车位”相当于鸡兔总只数，求摩托车和三轮车各有的辆数相当于求鸡兔各有的只数。只要套用刚才的模型就能解决问题，这里学生会遇到每多一辆三轮车，总轮数还是否多2的问题，也就需要重新理清“为什么每多一只兔总脚数就会多2”的问题。设计例题二的原因不单是让学生体验情景对象上的变化，更重要的是让学生体验问题的本质和模型的由来。

通过综合两个例题，进一步理解模型本质，教师可以引导学生用自己表达方式。如果用对象1和对象2比喻成刚才例题中的鸡和兔、三轮车和摩托车，用对象1和对象2的总脚数比喻成鸡兔总脚数、三轮车和摩托车总轮子数，要求的是对象1和对象2各有的只数，那么模型就有一个比较具体的表达，随意假设对象1和对象2相应只数后所得模型：

（4）识破变式，看透问题本质

經历第二例题的情景与对象的变化，创设例题三以求突破。例三：六1班全班同学参与植树节活动，全班共20人，每个男生负责植树5棵;每个女生负责植树3棵，一共要种76棵树，问男女生各多少人？相对例一、二里面的对象属性，“三轮车和摩托车”与“鸡与兔”具有明显的相似性，学生需要辨识例三是否属于同类型题目。

随意假设有19个男生，1个女生，那么就有19×5+1×3=98棵树，比实际植树数多，说明男生假设得多了，女生少了，下面需要知道男生和女生人数与实际相差多少个，利用模型解决问题：

所以男生实际人数：19-11=8（人）女生实际人数：1+11=12（人）

通过多层例题，看透一个本质，强化对模型应用，深刻理解了鸡兔同笼模型的意义和由来，培养学生的抽象思维。

3、验证模型

验证模型也是数学建模里面的一个必要环节，不单只是建设模型，验证和校对模型同样是确立模型的关键，在小学数学的解决问题里，“验证模型”更像是在检查解决过程的合理性，验算结果的正确性，对问题进行二次思考与回顾。例如对例题三的验证：8×5+12×3=76（棵），也可以通过列表和观察数据的变化，判断出“总脚数差值”、“单个脚数差值”和“与实际相差的只数”三者关系是否符合模型要求。

学生经历参与模型的建立，理解模型由来，看透问题的本质，最终理清特定问题的数量关系的意义，深刻体验某种数量关系与特定问题的关联性。而非强调借助记忆力辨别类型题目对应类型模型，从而缺乏对数量关系摸索的深度参与。

三、鸡兔同笼的建模教学方法与传统的对比

由于学生在四年级还没有接触列方程求解，教师在教授“鸡兔同笼”问题时多用抬腿法、假设法等方法讲解题目，用假设时一般会直接假设全部是兔或全部是鸡的只数，如果当堂教师没有揭示为什么要这样假设，学生解题时容易局限于形式套路，着重发挥记忆和重复训练的效果来达到解题目的，没有真正看透假设法的本质意义。利用数学建模的方法则是着重于引领学生观察和分析问题，通过多层问题的探索而确立数学模型，发掘问题的本质。整个学习过程的时长可能会超出一般课时的规定，但这样能够充分开发挥学生的思维深度，重视建立数量关系模型，把握解决问题的核心。

参考文献

[1]张奠宙.小学数学研究[M].高等教育出版社，2008.

[2]师天龙.论小学数学应用题教学中数量关系分析能力的培养[J].科技资讯，2020（13）

[3]杨贵玲.拓展思维，强化实践——小学数学应用题解题的教学策略[J].课程教育研究，2017（30）