大规模数据集Spark并行优化谱聚类

吕洪林,尹青山,2

(1. 辽宁对外经贸学院,辽宁 大连 116052； 2. 吉林大学,吉林 长春 130000)

谱聚类能够基于数据的非线性核距离对数据集进行归类，从而挖掘数据背后的隐藏价值，成为近年研究热点[1-2]。但随着互联网和信息传输能力的发展，以大数据为特性的TB甚至PB级的大规模数据集已经成为常态，经典谱聚类对于大规模数据集的运行时间及计算瓶颈越来越突出[3]。

为此，已有研究提出了各种改进的谱聚类算法。文献[4]通过数据采样预处理提取核心点集，借助一致性理论由核心点集完成大规模数据集的快速谱聚类。文献[5]通过Leaders算子初始聚类控制抽样子集对原始数据类别的覆盖，再通过子集部分核矩阵完成大规模集谱聚类。文献[6—7]提出使用Nyström近似技术避免计算整个相似矩阵，取得较好的加速效果；文献[8]提出共享近邻约束谱聚类，用共享近邻去衡量数据相似性，用主动约束描述数据关系，实现增量式聚类。

随着分布式并行框架的兴起，文献[9]研究了近似密集相似计算方法，分析了Nyström与稀疏矩阵方法；文献[10]以MapReduce框架并行优化谱聚类，提高算法的运算效率和性能，其聚类速率随数据规模的增大呈近似线性增长；文献[11]以MapReduce框架对初始聚类数据并行地进行K-means迭代聚类，获取大规模数据集的快速高效聚类；文献[12]基于轮廓系数和Spark框架并行改进相似距离计算，有效提高了谱聚类的准确率和扩展能力。

并行化有效提升谱聚类在大规模数据集上的聚类性能，但与HDFS等主流系统的兼容性有待提高。当前Spark技术已成为大数据处理的主流平台，其RDD和DAG抽象极大地提高了数据挖掘的并行分析性能。为此，本文提出适于谱聚类在大规模集应用的Spark框架并行化算法，通过试验结果验证改进算法在大规模数据集下良好的聚类性能和可扩展性。

1 谱聚类并行优化

1.1 相似矩阵并行计算

谱聚类算法中的相似矩阵主要由所有样本之间的两两相似信息构成，在大规模数据集下，对所有样本计算相似度将带来难以承受的计算开销甚至导致聚类失败，为此，采用分布式并行算法运算复杂度将由原始算法的O(n2)降低为O(n2/p)，其中p为计算并发度，同时采用t近邻[7]方法对稠密相似矩阵进行稀疏化。

在大规模集上相似矩阵占用较大的存储开销，为此，采用t近邻[7]和倒排索引进行矩阵稀疏化和对称性快速修复[13]。对每个样本xi进行t近邻相似过滤，得到距离最近的t个邻居，组成集合Sset[xi]

Sset[xi]={([xi],sim(xi,x1)),…,([xi],sim(xi,xt))}

(1)

式中，[xi]为样本xi的序号；sim(xi,xt)为两样本的相似度值。t近邻稀疏化后，对相似矩阵进行对称性修复，如图1所示，以xi的邻居xj的序号作为KEY值，收集其Sset[xi]，倒排后与Sset[xi]进行“或”合并，从而得到xj的所有相似度信息，实现矩阵的对称性修复。

1.2 矩阵并行正规化

根据单向迭代和t稀疏化计算样本的相似矩阵W={wi,j}后，由其对角矩阵D={Di,j}得到经典谱聚类算法计算样本的Laplacian矩阵及其正规化计算式

L=D-W=D-1/2·L·D-1/2

(2)

其中，对角矩阵的计算式为

(3)

经典并行谱聚类算法需要大小为N×N的2个矩阵存储，空间需求较大。因此，对W通过相应位置变换构建Laplacian矩阵，其过程如图2所示。

首先以行为单位，并行计算W每行元素的和，如图2(a)所示，W的行元素代表了样本的相似度集合信息，图中IndexArr()为与当前样本相似的其他样本的序号集，而VarArr()描述了该相似值。在计算行元素的和之后，为每行增加对角索引号，并将D中非零对角元素添加到W矩阵的相应对角元素位置。最后对W非对角元素值取反，如图2(b)所示，则可以构建Laplacian矩阵。

根据式(2)所示，Laplacian矩阵L的正规化通常通过矩阵连乘完成，其复杂度较高，达到O(n3)[14]。为此，将矩阵连乘转换为标量与矩阵相乘的形式[13]，其计算复杂度相应的降为O(n2/p)。

整个计算过程见表1，计算对角矩阵后，利用Spark框架的broadcast机制将其各元素分配到对应的节点内，各计算节点完成矩阵相应元素取反及添加索引操作。

1.3 特征向量计算并行化

谱聚类需求解Lnorm的前k个特征值对应的特征向量，构成降维矩阵，文中采用并行近似特征向量计算代替经典谱聚类中的精确特征向量计算，以加速大规模集特征向量的计算过程。目标函数为

(4)

根据最大可分理论将式(4)目标函数转换为方差最大的向量形式，即

(5)

并可以通过拉格朗日乘的方法转化为

LInvy=λDλ

(6)

式中，LInv为L的取反矩阵，根据式(6)可知计算LInv的前k个特征向量即得到传统谱聚类的最优解。基于PIC算法思想[15]可得迭代计算式为

vi+1=LInvvi

(7)

式中，i为迭代次数，当其足够大时，对v(i)进行聚类可得最终谱聚类。基于LInv的稀疏特性，文中将样本数据视为有向图，并根据图的消息传递机制进行近似特征向量的并行迭代。Laplacian矩阵L的正则化并行计算如下。

输入 相似矩阵W

输出 正规化L矩阵

函数 diagM←simM.map(e.count)broadcast();

主体 ∥正规化过程

lapM←simM.map{

FOR each linee

IF diagM[e]==0

SP中的每一个值：arr_v=0；

ELSE

arr_v=arr_v×(diagM[e])-0.5；

}

lapM←lapM.map{

FOR each linee

FORi:SP.arr_value.length

IF diagM[e]==0

arr_v[i]=0；

ELSE

arr_v[i]=arr_v[i]×(diagM[i])-0.5；

}

∥lapM采用RDD[SP]的形式进行存储；

lapM:RDD[SP]；

1.4 K-means聚类并行化算法

谱聚类算法中K-means聚类的并行计算通常为初始聚类中心获取并分发到各分布式节点中，计算各节点中样本与初始中心的距离，迭代更新聚类中心及距离，直到达到预设的迭代最大次数或误差限。因此，并行计算中距离的计算仍产生很大的计算量和节点间通信开销，为此，文中采用样本二范数关联的方式优化K-means聚类过程中的距离计算。

(8)

realDis=(a1-a2)2+(b1-b2)2

(9)

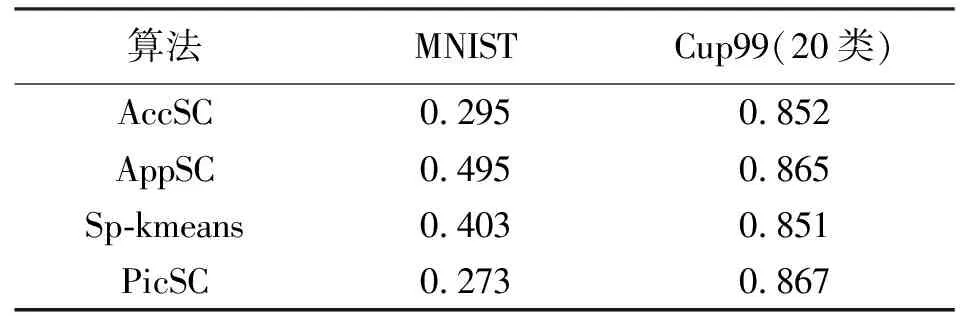
显然boDis值小于等于realDis值，由于节点中的各个样本或聚类中心都会事先计算并记录boDis值，因此在K-means聚类过程计算距离时，先进行如下比较过程：①初始化样本与其最近聚类中心的距离bDis，然后比较boDis与bDis的值大小；②若boDis大于等于之前计算的bDis最小值，说明realDis不可能小于bDis最小值；③若boDis小于bDis最小值，则计算realDis，当realDis

2 试验分析

为验证文中并行优化算法(记为AppSC)的聚类性能，试验采用手写字集MNIST[15]和网络攻击统计数据集Cup99[16]作为试验数据，由8节点192 GB内存的计算机群搭建试验环境，Spark框架采用V2.0.1版本，MNIST集的样本数为10 000，特征数为856，特征类别为10，Cup99集样本数为400 000，特征数为45，特征类别为35。

以精确特征向量并行谱聚类(记为AccSC)，基于Spark并行计算框架的K-means并行优化算法(记为Sp-kmeans)[14]及PIC快速迭代聚类算法(记为PicSC)[9]作为性能对比算法，以归一化互信息(NMI)作为性能评价指标，NMI∈[0,1]值越大表明算法的聚类性能更优。

2.1 聚类的效果比较

以MNIST手写集和类别数20的Cup99集为数据，比较各算法的谱聚类效果，试验中算法分别进行50次取各试验的平均NMI作为试验，其值见表1和表2，其中表2试验进行了t近邻稀疏处理。

表1 平均NMI值试验结果(未进行稀疏处理)

表2 稀疏化后的NMI试验结果(t=200)

从表1和表2试验结果中可以看出，基于精确特征向量的AccSC算法在不同的试验数据集上均取得较好的聚类性能，文中算法采用近似特征向量替换，其聚类性能相比EigSC算法聚类性能有所下降，但仍比另外两种算法的聚类性能更优，验证了采用近似特征向量替代精确特征向量计算的有效性。表3中试验数据的相似矩阵在经过t=200近邻稀疏化后，虽丢失部分相似度信息，但对比表2和表3中相同算法的试验结果可以看出，经稀疏处理后算法得到的NMI值更优，说明合理的t值设置不仅有效减少了算法对于大规模集谱聚类时的存储开销，而且一定程度提高了算法的聚类性能，后续试验采用t=200近邻稀疏。

2.2 特征向量求解时间试验

本节主要对谱聚类中的耗时较大的相似度计算及特征向量求解进行运算效率试验比较。从Cup99数据集中抽取0.1、0.5、1、2、5、10万条样本，并将数据存储于HDFS中。首先对文中单向循环迭代相似度计算(记为Mulit)及传统数据广播式相似计算(记为DataBC)进行运行时间对比试验，结果如图3所示，近邻稀疏处理t=200。

从试验结果可知，Mulit方法具有良好的计算效率，性能优于DataBC方法，且随着数据集规模的增加，优势更为明显，数据集规模的增加对Mulit方法的运算时间影响变化较小，主要由于其不仅保证样本相似度的单次计算，且避免了DataBC方法对大规模集时主节点压力过大产生的性能瓶颈。

2.3 扩展性能测试

采用不同数据规模的Cup99集数据分析文中改进算法的适应性试验，试验统计各算法在不同规模集上的运行时间，如图4所示，图中试验结果为50次运行时间的平均值。

从图4可以看出，AppSC、AccSC、Sp-kmeans和PicSC算法在不同规模数据集上均表现出较好的可扩展性，AppSC和PicSC两种算法的平均用时对数据集的规模不敏感，表现出更优的可扩展性，主要由于近似特征向量的使用使数据规模的增加仅影响了算法的迭代次数，获得线性增长的运算复杂度。Sp-kmeans算法的距离计算时间消耗及AccSC算法的精确特征向量计算均会受到样本数据规模的影响，因而运行时间受样本影响最大。

综合试验结果，文中算法在并行优化和近似稀疏基础上，进一步采用近似特征向量求解方法，取得与精确特征向量算法相近的聚类效果，但有效减少了算法复杂度，表现出较好的扩展性和稳健性。

3 结 语

为解决大规模数据集谱聚类的计算耗时等性能瓶颈，基于当前Spark技术主流并行框架，提出了一种用于大规模集聚类的改进并行算法，算法对相似矩阵稀疏化、Laplacian矩阵的构建、K-means聚类过程距离计算进行并行优化，同时采用近似特征向量计算进一步减少计算量，并分析了近特征向量的有效性。试验结果验证了算法在大规模数据集下良好聚类性能可扩展性。

但文中算法还需进一步研究并行算法中t近邻、特征向量维数等参数的自动调优，以充分发挥算法的性能优势。