一种高光谱遥感图像快速谱聚类算法

张亚平，张 宇，杨 楠,2，罗 晓，罗 谦

(1. 哈尔滨工业大学交通科学与工程学院，黑龙江 哈尔滨 150090; 2. 国土资源部城市土地资源监测与仿真重点实验室，广东 深圳 518034; 3. 中国民用航空局第二研究所，四川 成都 610041)

谱聚类算法作为聚类分析中的一个全新分支，无需对数据的全局结构作出假设，适用于任意空间分布数据的聚类，具有识别非凸分布数据、高效聚类的能力，适合于解决诸多实际问题，因而在短短的几年时间里就引起了中外学术界的广泛关注。近年来，国内外学者在谱聚类算法理论和应用研究方面展开了大量研究工作，取得了诸多理论和应用方面的研究成果，促进了谱聚类算法体系及其应用技术的发展。目前，谱聚类算法已经成功应用于人脸识别[1]、图像分割[2]、医学图像分析、信息检索[3]、电力系统建模[4]、蛋白质数据分析[5]等领域。

本文的待分类图像为高光谱图像，文献[6]对高光谱图像的分类算法进行了系统性的介绍。当前，关于遥感图像的机器学习算法的研究很多，如文献[7]利用SVM研究了几何特征、图论特征对土地利用分类的影响，文献[8]利用卷积神经网络对地表覆盖类型的分类精度进行评价，文献[9]将FSVM算法与ISODATA算法相结合，新的算法更适用于高分辨率遥感图像，分类精度也得到了较大提高。但是关于遥感图像的谱聚类算法的研究却很少。本文将非监督分类算法在机器学习领域中的研究成果引入遥感图像数据处理领域，尝试应用集成在Sklearn模块中的快速解求大规模矩阵端元奇异值的Lanczos算法[10]来求解拉普拉斯矩阵的少数最小特征值及其对应的特征向量，以解决谱聚类算法计算效率过低的问题，实现能够区分遥感图像像素空间分布形态复杂的点群的非监督分类算法；然后与传统的K-均值算法数据进行对比，发现谱聚类算法易于识别线性地物，说明其应用于遥感图像分类的可行性。

1 谱聚类算法

聚类算法主要包含构成图和裁剪图两个步骤。先由众多数据点构成一张图(graph)，然后再按照一定的准则进行切图(graph)。主要的切图规则有最小割集规则(minimum cut)、平均割集规则(average cut)、规范化割集规则(normalized cut)、比例割集规则(ratio cut)等[11]。

1.1 最小割集规则

最小割集规则较适宜于将谱图G分割为A、B两个子图的情况。A、B两个子图合并起来即为G，且A、B之间没有重叠。即A∪B=G，A∩B=∅。定义一个不同边权重之和的损失函数为

(1)

最小割集规则为cut(A,B)等于最小值时的分割规则。使用最小割集规则对谱图进行分割可以取到很好的聚类结果，但是这种分割规则只考虑了两个子图之间的权值，没有考虑子图内部的权值问题，致使较易发生谱图歪斜偏向小区域分割的现象。因此，学者们还提出了规范割集规则与比例割集规则，以防止谱图歪斜分割的问题。

1.2 规范割集规则

定义一个目标函数，目标函数为Ncut(A,B)，当致使目标函数Ncut(A,B)最小的时候的一种谱图分割规则称为规范割集规则。目标函数Ncut(A,B)为

(2)

该规则不仅可以量度簇内样本间的相似程度,还可以量度簇间样本间的相似程度。

1.3 平均割集规则

平均割集规则目标系数Avcut(A,B)为

(3)

式中,|A|、|B|分别代表给A、B子图各自的顶点数目。该规则的目标函数表示A、B子图各自与损失函数的比值之和。

1.4 比率割集规则

比率割集规则目标函数Rcut(A,B)为

(4)

式中，|A|表示A子图的顶点个数；|B|表示B子图中的顶点个数。当目标函数最小时，簇间样本数据的相似性最小。

1.5 谱聚类算法图像矩阵

谱聚类算法的流程如图1所示，可以划分为以下几个主要步骤：①相似度矩阵计算；②度矩阵的计算；③拉普拉斯矩阵的计算；④特征值与特征向量的计算；⑤K-均值聚类。主要包括相似度矩阵、度矩阵、拉普拉斯矩阵3个重要矩阵。

1.5.1 相似矩阵

相似矩阵A为一个对称矩阵，它的每个元素是由不同样本之间的相似度组成的，相似度一般由样本之间的距离来度量，也有用高斯核函数与余弦相似度来度量的。如果用距离来度量样本相似度，通常矩阵中只保留距离小于给定阈值的相似度值，此时的矩阵A称为K-邻域矩阵，是一个稀疏对称矩阵。有许多表示样本点之间距离的方式，最常见的是欧氏距离。欧氏距离的公式为

(5)

式中,向量xi和xl(i,l=1,2,…,n)为遥感图像中的两个像元；n代表遥感图像像元总数。

当使用高斯核函数计算相似矩阵A时，核函数中的参数σ代表核函数的响应宽度，与K-邻域矩阵中的阈值K具有相同的作用，此时的相似矩阵A实质上稀疏核矩阵。给定遥感图像中的两个像素向量xi和xl(i,l=1,2,…,n)，n代表遥感图像像素总数，则高斯核函数可表示为[12]

(6)

1.5.2 度矩阵

度矩阵D(degree matrix)是一个对角矩阵，是在矩阵A的基础上得到的派生矩阵。其对角线元素为矩阵A中相应的行或列的所有元素之和。矩阵D可以表示为[13]

(7)

1.5.3 拉普拉斯矩阵

拉普拉斯矩阵L也称为导纳矩阵、基尔霍夫矩阵，是图论中一个图(graph)直观的矩阵表示。拉普拉斯矩阵主要有以下几个特征：①拉普拉斯矩阵为对称阵，且特征值非负，即为半正定矩阵；②拉普拉斯矩阵的零特征值的个数即为图连通区域的个数；③拉普拉斯矩阵最小的非零特征值与图的代数连通度相等；④拉普拉斯矩阵每一行之和均为零。由相似矩阵A和度矩阵D得到拉普拉斯矩阵的数学基础公式为[14]

L=D-A

(8)

谱聚类算法的核心部分是解求拉普拉斯矩阵L的特征值和特征向量，而一幅遥感图像的像素数目一般在数万以上，如何快速解求这一超高阶拉普拉斯矩阵的特征值与特征向量问题，从而使谱聚类算法能够应用于遥感图像的非监督分类研究，是需要妥善解决的关键科学问题之一。这一尚待解决的关键科学问题的存在，也正是导致目前遥感图像处理领域尚无研究者应用谱聚类算法进行遥感图像非监督分类研究的原因之一。

2 高光谱图像谱聚类算法框架

高光谱图像的数据量大，常含有上百个波段。因此对算法的运算是一个挑战，在面向高光谱图像的谱聚类算法中，为了提升算法的运算速度集成了Lanczos算法，使得谱聚类算法更加快速。本文提出的高光谱图像谱聚类算法框架如图2所示。传统意义上的谱聚类算法主要分为非正则化谱聚类算法(Unnormalized spectral clustering)和正则化谱聚类算法(Unnormalized spectral clustering)。正则化谱聚类算法与非正则化谱聚类算法框架如下[2]。

正则化谱聚类算法框架：

输入：相似矩阵A∈Rn×n,聚类数目K。

(1) 由邻接权重矩阵构成相似图。

(2) 计算非正则化拉普拉斯矩阵L。

(3) 由拉普拉斯矩阵计算K个特征向量u1,u2,…,uk。

(4) 由特征向量u1,u2,…,uk组成特征矩阵U∈Rn×k的每一列，得到特征矩阵。

(5) 也可由yi∈Rk(i=1,2，…,n)组成特征矩阵的每一行，得到特征矩阵。

(6) 用K-均值算法将Rk空间中的数据划分为C1,C2,…,Ck个簇。

输出：A1，A2，…，Ak个类别。

非正则化谱聚类算法框架：

输入：相似矩阵A∈Rn×n,聚类数目K。

(1) 由邻接权重矩阵构成相似图。

(2) 计算非正则化拉普拉斯矩阵L。

(3) 由广义特征值公式Lu=λDu计算K个特征向量u1,u2,…,uk。

(4) 由特征向量u1,u2,…,uk组成特征矩阵U∈Rn×k的每一列，得到特征矩阵。

(5) 也可由yi∈Rk(i=1,2,…,n)组成特征矩阵的每一行，得到特征矩阵。

(6) 用K-均值算法将Rk空间中的数据划分为C1,C2,…,Ck个簇。

输出：A1,A2,…,Ak个类别。

遥感图像谱聚类算法是在Python集成开发环境(Python-IDEL)中，通过无缝集成Pyhthon-GDAL函数库和sklearn开源代码库实现的。遥感图像谱聚类算法需依次完成下列操作过程：遥感图像的输入操作，遥感图像的数据预处理，K-邻域矩阵或高斯核矩阵的计算，拉普拉斯矩阵构造，拉普拉斯矩阵特征值和特征向量求解，K-均值聚类算法输入数据构造(用拉普拉斯矩阵的数个最小特征值对应的特征向量构造新的待分类数据)，待分类数据的K-均值聚类分析，分类结果图像的输出，其算法框架可由图2表示。

由于遥感图像的类型较多，数据观测尺度和记录方式不尽相同。如多光谱遥感图像像元每个波段的DN值(Digital Number)为0～255的整数值，在进行谱聚类之前，可将DN值转化成实数值，公式为

(9)

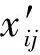
本文待分类的遥感数据为高光谱遥感数据，尽管各波段的光谱值为实数值，但是不同波段的光谱数据量纲可能不同，因此，需在分类前进行数据预处理以统一高光谱数据各波段的数据量纲。可运用数据正规化变换方法对高光谱数据进行预处理，公式为

(10)

式中,xmaxj和xminj分别为高光谱遥感图像第j波段光谱观测值的最大和最小值。正规化变换后的高光谱遥感图像各波段光谱取值为0～1之间的实数。

预处理后的遥感图像数据可以直接应用式(5)计算K-邻域矩阵或应用式(6)计算高斯核函数矩阵。在计算K-邻域矩阵时，距离阈值需要根据遥感图像数据的具体特征来确定一个适当值，如果该阈值过大，将导致相似矩阵A的非零元素过多，导致A不满足稀疏性；如果距离阈值过小，会丢失一些必要的像素相似性信息，使矩阵A不能正确反映遥感图像数据类群结构信息。在应用高斯核函数计算高斯核矩阵时，核函数响应宽度需要根据遥感图像的特征选取，过大或过小的响应宽度都会影响遥感图像分类效果。

计算出相似矩阵A之后，可以很容易地在矩阵A基础上构造拉普拉斯矩阵L，将矩阵A每一行(或列)全部元素求和，即可得到矩阵L的对角线元素。然后，将矩阵A的非对角线元素取相反数，即可获得矩阵L的非对角线元素。此时，拉普拉斯矩阵的构造过程结束。

当拉普拉斯矩阵L满足稀疏性时，可以用于Lanczos算法快速求解矩阵L的少数最大(或最小)特征值及其对应的特征向量。在谱聚类算法中，需要求出矩阵L的前G(G<

3 试验验证

为了验证算法的可行性，采用美国圣地亚哥市机场400×400×189的高光谱数据立方体(AVIRIS)进行分类试验，为使遥感图像的像元灰度值更加真实地反映地物的反射率，需要对遥感图像做大气校正。该研究区黑暗像元较多，因此采用忽略大气散射作用与相邻像元漫反射作用的简化黑暗像元大气校正法，采取的确定黑暗像素值的方法为波段最小值法。图3左、中、右分别为研究区域原图、谱聚类算法分类结果和K-均值算法分类结果。

由图3的谱聚类算法分类结果和K-均值算法分类结果对比分析可得，在谱聚类算法分类结果中停机坪上的两架飞机被很好地识别出来，对道路的区分也很好，但是在K-均值算法分类结果中却将飞机与地面划分为一类。对于图中右下角4栋房屋的顶面，因为日照角度的原因导致一侧上有阴影，反映在图像上房屋两侧的像元灰度值有差异，谱聚类算法据此将同一房屋的两侧分为不同的类，K-均值算法分类结果则并未出现这样的现象。由此可见，谱聚类算法易于识别K-均值算法不易识别的地物类别，即谱聚类算法对像元灰度值差异比较敏感。对于线性地物、两条不同材质道路的分界线谱聚类算法能较好地识别，而K-均值算法往往对道路的边界线(即灰度值突变处)反应不敏感。谱聚类算法的时间复杂度比K-均值算法高，因此运行速度比较慢，经过与Lanczos算法集成之后的谱聚类算法在运行速度上已经得到了比较大的提升，通过对谱聚类算法和K-均值算法分类,数目均设定为5个。两次的试验研究表明：K-均值算法的运算时间为45.9 s，谱聚类算法的时间为40多分钟，虽然集成Lanczos的谱聚类算法的运行效率仍低于K-均值算法，但却可以保证更高的分类精度。

4 结 语

本文提出了一种基于高光谱遥感图像的谱聚类算法，应用快速解求大规模矩阵端元奇异值的Lanczos算法求解拉普拉斯矩阵的最小特征值及其对应的特征向量，以此提高谱聚类算法的运算速度，初步解决了将谱聚类算法应用于遥感图像处理中运算速度慢的问题，并发现谱聚类算法易于识别线性地物，验证了谱聚类算法应用于遥感图像分类的可行性。