结合非线性贝叶斯反演算法的油田储层参数反演

张旭东，符华年，杨 崇

(宁波市测绘设计研究院，浙江 宁波 315042)

在石油开采过程中，若对油田储层变化信息掌握不及时，将无法制定合理的开采计划。若油层开采不合理，将会引起严重的地表沉降，不仅会破坏油井附属设施，降低石油的有效开采率，还会破坏周边建、构筑物，影响居民的生活和安全。在辽河盘锦地区，因石油开采引起的大范围地表沉降，严重破坏了当地的芦苇种植和河蟹养殖，损失巨大[1-2]。

石油勘探方法是获取油田储层信息的传统技术手段，该方法工艺复杂、过程烦琐、耗时耗力，难以实现对油田储层状态信息的实时掌握。地表沉降是油田压强变化、几何形状等储层信息在地表的直观体现[3-4]，借助地球物理反演方法，利用地表沉降信息可实时获取油田的储层信息。目前，国内外对于油田储层参数反演的研究较少，仍存在一定问题，如目前的确定性反演算法无法对反演结果的不确定性做出解释，单源模型反演精度有限等。

因此，本文以辽河盘锦地区作为研究区域，将随机反演算法中的非线性贝叶斯反演算法引入油田储层参数反演中，同时结合地球物理反演模型中适用性最强的Okada模型开展油田储层参数反演的研究，以期为油田储层参数反演提供一套稳定、可靠的反演算法。

1 反演算法及模型介绍

传统的确定性反演算法能够获取反演参数在数学上的最优解，但不能对反演结果的不确定性作出解释，是不完整的反演算法。随机反演算法通过获取模型参数的后验概率，不仅能够确定模型参数的最优值，而且能够对模型参数的不确定性作出解释，更具有实际意义[5]。因此，本文将随机反演算法中的非线性贝叶斯反演算法引入油田的储层参数反演中。

1.1 非线性贝叶斯反演算法

对于离散点的非线性反演问题，观测数据d等于模型参数m的非线性函数G(m)加上误差ε[6-7]，即

d=G(m)+ε

(1)

在贝叶斯框架中，后验概率密度函数p(m|d)描述的是在考虑先验信息的情况下，模型参数m能够解释数据d的概率，可以表示为

(2)

式中，p(d|m)是在给定数据d的情况下参数m的似然函数；p(m)为模型参数的先验概率密度函数；p(d)为一个与m无关的归一化常量，可将式(2)简化为

p(m|d)∝p(d|m)p(m)

(3)

先验信息是在反演之前预先知道的信息，先验信息来自相关的资料、已有的经验或主观的判断等[8-9]。似然函数可以被看作已知观测数据d的情况下随着模型参数m变化的函数，通常假设似然函数为多维高斯分布[10]，可以表示为

(4)

式中，N为数据点的总数；Σd为数据的方差-协方差矩阵，方差-协方差矩阵能够反映数据内在的不确定性。

通过贝叶斯式(3)计算得到模型参数的后验概率密度函数后，可获得反演参数解的所有信息，包括最大后验概率解、期望模型及单个模型参数的边缘分布[10]。

1.2 Okada模型

1985年，文献[11]通过对已有的弹性半空间断层引起地表沉降研究成果的分析，提出了有限矩形面源的断层位错模型，后来被人们称为Okada断层位错模型。

根据弹性半空间各向同性的位错理论，由于在弹性介质内的某一矩形面发生错动而引起地表某点的位移与该错动面的错动量成正比，唯一确定比例系数的是错动面的相对位置、错动面的几何尺寸、错动面的倾角、错动面的深度和弹性介质。建立以O为原点的空间直角坐标系，如图1所示。Okada模型的参数有7个，包括错动面的长度L、宽度W、倾角θ、走向φ、几何中心的深度d和在地表的投影坐标(x0,y0)。

2 试验分析

2.1 沉降资料获取

与水准和GPS测量相比，InSAR技术具有全天候、高精度、高效率、大范围等沉降监测优势[12-13]。因此，采用2007年1月至2010年9月的21景PALSAR数据，利用InSAR技术中的StaMPS技术对辽河盘锦地区进行沉降监测，具体数据处理流程见文献[14]，得到沉降监测结果如图2所示。

从图2中可看出，整个区域存在两个显著的沉降漏斗，Ⅰ区域最大沉降速率达到了-76.9 mm/a，Ⅱ区域最大沉降速率达到了-243.0 mm/a，与文献[15]的监测结果基本一致，说明该监测结果是可靠的。经资料调查，Ⅰ和Ⅱ区域的沉降漏斗分别对应于辽河油田的欢喜岭采油厂和曙光采油厂[16]，两个沉降漏斗与油田开采区域高度一致。

2.2 反演试验及分析

本文以InSAR沉降监测结果作为观测数据，基于非线性贝叶斯反演算法和Okada模型对油田的储层参数进行反演。研究区域内存在两个独立的沉降漏斗，本文选择以辽河油田最大的采油厂——曙光采油厂作为主要研究对象，展开油田储层参数反演研究。

2.2.1 结合单源Okada模型的油田储层参数反演

在反演过程中需要对InSAR沉降监测结果建立独立坐标系，参考基准点设在沉降中心，对应的地理坐标已知，泊松系数设为常用的0.25[17]。通过非线性贝叶斯反演算法，使用Okada模型对曙光采油厂的储层参数进行反演，取最大后验概率解为参数最优值，取2.5%～97.5%为参数的置信区间，因此在反演结果中包括了最优参数值和可靠区间。

考虑油层的存储状态，在使用Okada模型反演时，首先将倾角设定为0。反演得到的最优参数结果见表1，油层中心的平面坐标为(696.79 m，-973.12 m)，长为3 531.90 m，宽为1 702.56 m，油层走向为60.87°。反演得到的油层中心深度为939.90 m，经资料调查获知的实际油层埋深为765～920 m[18]，反演得到的油层深度基本符合实际油层深度。

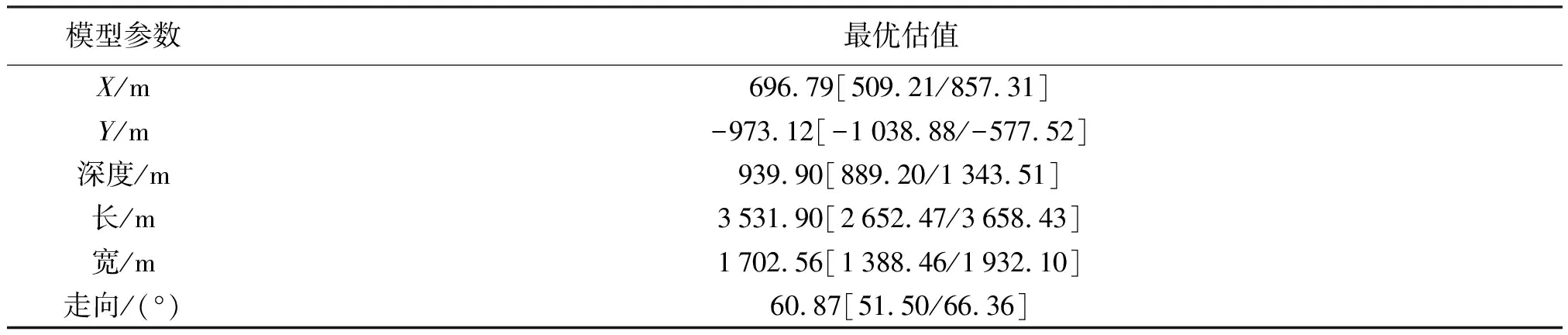
表1 Okada模型的最优拟合参数

观测和模拟地表沉降及残差结果对比如图3所示。基于最优参数组合，对油田地表沉降进行正演模拟，得到的正演模拟地表沉降结果如图3(b)所示。从图3中可以看出，Okada模型的模拟沉降与观测沉降非常接近，模拟效果较好。对观测沉降与模拟沉降之间的残差进行统计，得到残差分布直方图，如图3(d)所示，整体残差分布在[-60 mm，40 mm]，残差均值为-0.16 mm，标准差为15.91 mm。

为了更具体地判断沉降中心区域的模拟效果，将观测沉降结果与模拟沉降结果沿剖面线A1A2的沉降值刻画出来，如图4所示。从图4中可以看出，在A1A2剖面线上存在两个沉降漏斗，而使用单源Okada模型仅能拟合出一个沉降漏斗，与观测沉降存在较大的误差，说明单源Okada模型不符合该地区油田储层变化与地表沉降之间的映射关系。

2.2.2 结合双Okada模型的油田储层参数反演

由上节可知，单源Okada模型对油田储层参数反演的精度是不够的。本文将双Okada模型引入油田储层参数反演中，探究双Okada模型对油田储层参数的反演效果。双源模型即假设油田地表沉降是由地下两个油层变化引起的。

假设油田地表沉降是由地下两个倾角为0的油层共同作用下引起的， 则使用双Okada模型对油田储层参数进行反演。通过双Okada模型反演得到的最优参数结果见表2，使用最优参数组合正演模拟的地表沉降结果如图5所示。

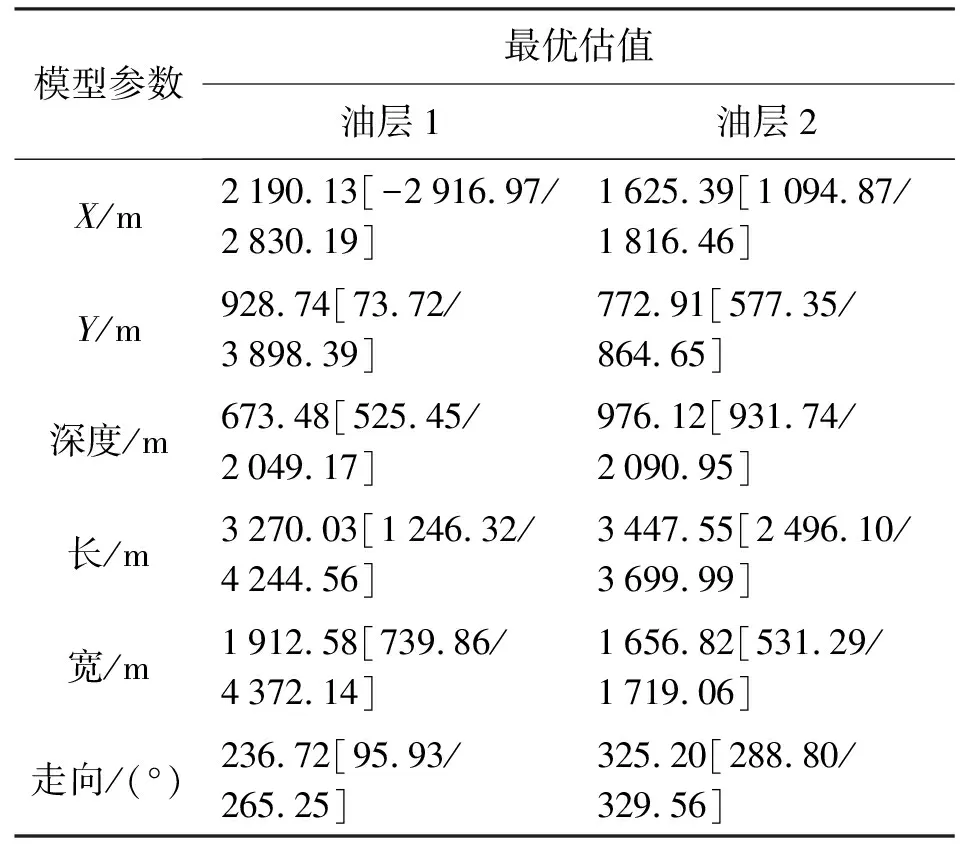
表2 双Okada模型的最优拟合参数

通过表2可知，通过双Okada模型对油田储层参数进行反演，得到两组储层参数。油层1中心的平面坐标为(2 190.13 m，928.74 m)，深度为673.48 m，长为3 270.03 m，宽为1 912.58 m，走向为236.72°；油层2中心的平面坐标为(1 625.39 m，772.91 m)，深度为976.12 m，长为3 447.55 m，宽为1 656.82 m，走向为325.20°。实际油层埋深为765～920 m，双Okada模型反演的两个油层深度均基本符合实际油层深度。

从图5(b)可以看出，双Okada模型的模拟沉降与观测沉降更为接近，不仅能够较为完整地模拟出沉降中心区域，在沉降中心以外的区域也有较好的模拟效果；从图5(c)残差图可以看出，整个区域的残差分布较小且相对均匀。对残差进行统计，得到残差分布直方图，如图5(d)所示，整体残差分布在[-40 mm，40 mm]，残差均值为-0.13 mm，标准差为12.53 mm。

与单源Okada模型相比，通过双Okada模型模拟的地表沉降结果精度更高，反演得到的储层参数更可靠。

3 结 语

本文以辽河盘锦地区作为研究区域，以InSAR沉降监测结果作为观测数据，首次将非线性贝叶斯反演算法引入到油田储层参数反演中，并结合Okada模型对油田的储层参数进行反演，得出具体结论如下：①非线性贝叶斯反演算法不仅能获取模型参数的最优值，还可以对反演结果的不确定性作出解释；②从剖面线A1A2的沉降变化趋势可知，单源Okada模型不符合该地区油层参数变化与地表沉降之间的映射关系；③基于双Okada模型反演得到的两个油层深度均基本符合实际油层深度，且正演模拟得到的地表沉降与观测地表沉降之间的残差更小，说明双Okada模型更符合该地区油层参数变化与地表沉降之间的映射关系。

本文利用地表沉降信息对油田储层参数进行反演，取得的研究成果可为国内外其他油田的储层参数反演提供重要的技术参考。