一种基于北斗导航系统的多天线定向测姿方法研究

2020-01-03简海波

测绘通报 2019年12期

简海波，汪捷

(海军工程大学电子工程学院，湖北武汉 430033)

2018年12月27日，中国自主研制的北斗导航系统正式开放全球定位服务，这将对卫星导航技术的研究和应用带来深远影响[1]。卫星导航具有全天候、全地形等优势，在国民经济和社会发展的各个方面应用广泛。其中，早在21世纪初期利用卫星导航技术实现物体定向[2]已经开始了研究和应用，在定向的基础上实现姿态测量[3]俨然是现在研究的热门。传统的姿态测量手段多以惯性器件为主。惯性器件测量姿态具有稳定度高，测量快速等优点，但是惯性器件具有误差积累[4]，在较长时间后，无法保证高精度姿态信息的输出。在追求效率的时代，无论是军事应用还是民用都在想办法提高或改变姿态的测量方式。因此，本文提出一种基于北斗的多天线姿态解算方法。

1 北斗定向测姿原理

通过任意布设的三天线只要满足天线不共线就可以得到2个不相关的基线向量，通过向量的投影关系及向量和平台坐标的转换关系即可得到平台的三维姿态信息[5-6]。

偏航角为

(1)

俯仰角为

(2)

滚动角为

(3)

式中，xli、yli、zli均为坐标转换之后的基线向量坐标。三天线测姿方法可扩充至四天线以上，当采用四天线以上的姿态测量时，可以对基线向量进行网平差运算[7]。

2 单频单历元模糊度解算方法

各个基线向量解算的过程中，关键是模糊度的快速精确固定[8-9]。由于平台的天线阵列基线长度已知，可以改进载波相位差分定位中的模糊度算法，在LAMBDA算法[10]中加入限定方程可使得单频单历元的LAMBDA解算系数矩阵不再秩亏[11]，这种方法也称CLAMBDA算法或阻尼LAMBDA算法[12]。

根据LAMBDA算法，模糊度参数a的搜索空间可以充分利用基线长信息限制基线分量的二次型最小

ΩF(χ2)={a∈Z|F(a)≤χ2}

(4)

其中

(5)

(6)

ΩF(χ2)⊂ΩE(χ2)

(7)

ΩF(χ2)={a∈Zn|F(a)≤χ2}

(8)

(9)

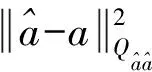
根据CLAMBDA方法的原理，设计CLAMBDA方法的具体实现流程如下：

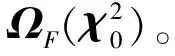
(10)

(11)

(12)

式(12)可以保证在进行模糊度搜索时，至少有一个整数模糊度候选点，并且满足对应的F(a)不大于χ2(0)。

(2) 根据SE-VB算法[13]求取第一个整周模糊度候选解a1。首先要求解基线分量b，式(6)满足如下函数模型

(13)

(14)

(15)

式中，Δb=[ΔxΔyΔz]T。对式(15)进行经典的最小二乘平差，可求出b1。再将b1作为初值进行最小二乘解算，重复以上迭代步骤直到bn和bn-1的差值小于设定的阈值。此时b=bn。再根据式(5)、式(6)即可求取F(a1)。

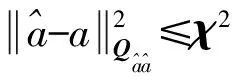
由于加入了基线长约束条件，模糊度最优解必须同时满足模糊度和基线向量的二次型最小，此时模糊度搜索空间[14]已经不为椭球。相比无基线长约束，基线长条件缩小了模糊度的搜索空间，提高了模糊度的搜索效率。由于模糊度最优解同时要满足基线向量二次型最小，因此该方法还可以在一定程度上提高基线向量精度[15]。上述算法在模糊度没有周跳[16]的前提下可以有效地解算单频单历元基线向量。

3 试验案例

根据一组天线观测数据，利用自编解算程序模拟姿态测量。分别对三天线姿态测量和四天线平差测量的结果进行比较。总共接收4个天线的数据，其中主天线与其余天线之间的距离分别为9.910、15.219、18.103 m。利用3个天线进行直接姿态测量得到的姿态信息和四天线平差结果如图1所示。

从图1和图2中看，平差计算平滑了姿态数据曲线，使姿态测量误差更小，通过与惯性测量仪器输出的姿态信息进行比对，直接测量误差约为0.12°，采用四天线平差处理的测量误差约为0.107°。

为了进一步验证本文提出的姿态测量算法在动态基线解算中的可行性，进行了动态三天线姿态解算试验。三天线均架设于观测状况良好的屋顶试验平台，试验过程中，先保持三天线静态测量数分钟，而后模拟平台运动，将其中一个接收机天线上下运动一段时间，然后回到初始位置静态测量数分钟。得到的三天线观测数据进行姿态解算结果如图3所示。

从图3可以看出，姿态的变化可以分为3段，0～200历元属于静态，在200～300历元姿态来回变化，在300～450历元姿态重新回复稳定。验证了此方法可用于实时姿态测量。