敏捷遥感卫星新型姿态控制精度评估方法

凌琼 董天舒 谭志云 侯锐 矫轲 张雷 赵峭

(北京空间飞行器总体设计部，北京 100094)

随着航天技术的快速发展，对地面特定目标的观测任务要求越来越高，出现了非沿迹多条带成像、目标凝视、立体成像等工作模式，能执行这种任务的卫星都称为敏捷卫星。卫星敏捷性主要体现在姿态大角度快速机动，且机动过程中姿态保持高精度、高稳定性。敏捷卫星可以利用自身的机动性，在短时间内迅速改变其相机对地指向，大大地提高对地观测的效率和灵活度。相较于采用传统的三轴稳定对地指向成像模式的观测卫星，高分辨率敏捷卫星对平台技术的需求已发生了本质的改变[1-3]。对于具备姿态机动路径自主规划能力、支持边机动边成像的新型遥感卫星而言，姿态敏捷机动核心技术地面验证待解决的问题有两个：一是需要进行相机目标成像轨迹正确性判读，即机动速度指标、姿态指向精度判读；二是由于机动过程中可成像，还需关注姿态机动对成像质量的影响，如针对成像过程中姿态稳定度进行评估。

为解决以上问题，本文提出一种基于载荷成像点轨迹的敏捷卫星姿态品质评估方法。根据航天器轨道、姿态数据计算得到星载相机对地摄影轨迹、摄影点对地扫描速度等参数，对成像过程中姿态指向精度、姿态稳定度等指标进行直观量化判读。实际上，影响载荷成像点轨迹位置精度的因素不仅有姿态指向误差，还包括定轨偏差、星上规划计算模型误差、相机安装偏差、结构热变形等诸多因素。为简化问题模型，选择姿态指向误差作为主要影响因子进行研究。同时，为了提高高原、山区地形的成像点计算精度，要引入地表高程数据进行模型修正。该方法对于航天器敏捷机动关键技术性能评估，以及航天飞行任务模式的分析和论证，都有积极意义。

1 方法设计与实现

1.1 研究对象

敏捷工作模式是传统的光学遥感卫星成像工作模式的扩展，高分辨率敏捷卫星以大角度快速姿态机动及稳定能力、面向星上资源的任务规划能力、高精度时空信息测量能力等核心技术为特点[4-6]。本文提出的敏捷机动姿态品质评估方法针对该类卫星开展研究，选取采用遥感公用平台的某卫星为应用研究对象，图1～图4为某卫星的敏捷成像工作模式示意。

地面成像任务上注后，星上首先进行用户任务解析，并分发载荷子任务、姿态子任务至相关智能单元。控制分系统收到整星分发的姿态控制子任务后，自主进行姿态规划并按照规划时间进行姿态机动，以配合载荷成像。关于用户任务，可通过地面仿真确认任务选取是否合理，星上机动能力能否满足等，仿真过程数据如姿态、镜下点运行轨迹等，成为地面测试分析重要数据来源之一。

针对星上自主规划路径并进行姿态机动、机动过程中可持续成像两个特征，提出一种根据成像点轨迹进行姿态指向精度、姿态稳定度分析的方法。以Matlab为计算平台，建立星体坐标系-地固系算法模型，根据卫星定轨数据以及卫星高精度姿态数据，计算得到星载相机成像点轨迹，通过与目标成像轨迹比较，获得更为直观清晰的量化判读结果，实现姿态指向精度、姿态稳定度的直观量化判读。

注：A1～A4为成像前姿态机动完成点，B1～B4为成像任务起点，C1～C4为成像后姿态机动起点，MS为整体任务姿态机动起点，ME为整体任务姿态机动完成点。

图1 同轨多点目标成像

Fig.1 Points imaging

图2 同轨被动多条带拼幅成像

图3 同轨主动多条带拼幅成像

图4 非沿迹主动推扫成像

1.2 算法流程

新型姿态控制精度评估算法流程如图5所示，主要分为3个步骤：①待分析数据的筛选与匹配；②根据卫星姿轨数据计算得到卫星相机光轴矢量在地表的扫描轨迹；③根据计算结果对不同条带的姿态控制精度进行评估，包括姿态机动速度指标符合性判读、成像时段内姿态指向精度以及姿态稳定度指标符合性判读。步骤1针对不同源的数据进行裁剪、过滤以及匹配性处理；步骤2之成像点轨迹求解算法为算法核心模块，计算过程复杂，且要求较高计算精度，以保证评估结论的可信度；步骤3根据算法条件识别不同类型条带，并对每条带的姿态机动速度指标、姿态指向精度和姿态稳定度进行判读。步骤1、3均是针对具体数据进行的数据甄选、过滤操作，文中不予关注，下文主要针对步骤2的核心算法进行介绍。

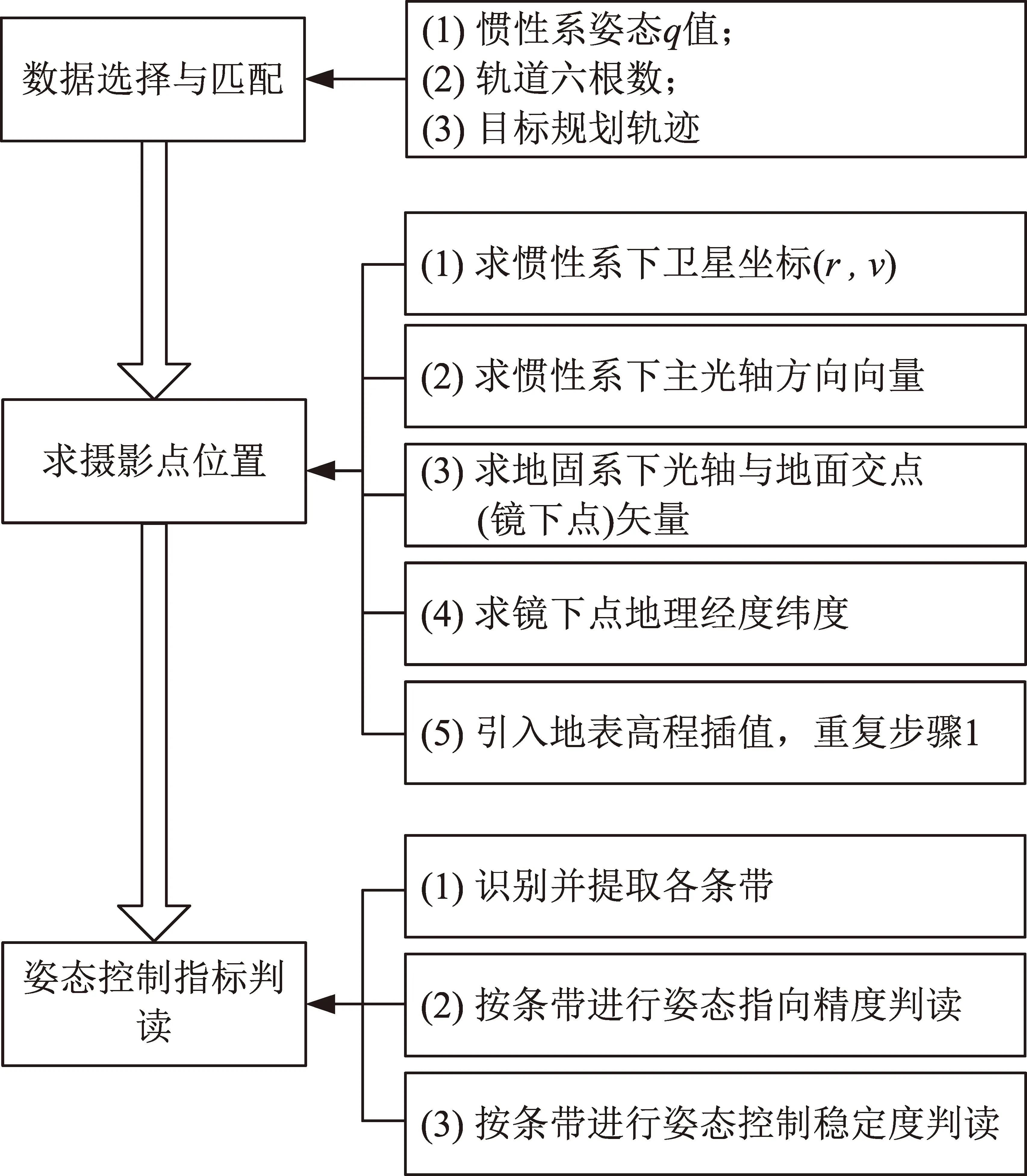
图5 算法流程示意

1.3 核心算法实现

在地心赤道惯性坐标系下，轨道六根数意义如图6所示。图6中N指示卫星轨道与赤道平面的升交点，P指示卫星轨道的近地点，Ω为升交点赤经，ω为近地点幅角，e为偏心率，f为真近点角，i为轨道倾角。用轨道六根数描述卫星在空间中的运动特性，则卫星的向径r和速度ν可表示为轨道六根数的函数。

图6 卫星轨道六根数含义

由经典轨道根数求卫星惯性系OXYZ下位置r和v的步骤如式(1)～(4)所示。

(1)

(2)

(3)

(4)

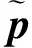
(5)

若卫星的相机视方向和星体OZ轴一致，则在惯性系下相机的视方向矢量以表示为式(6)；如不一致，则可表示为式(7)，其中K为相机的安装矩阵，或者在轨考虑形变后的修正安装矩阵。

t=M·[0,0,1]T

(6)

t=M·K·[0,0,1]T

(7)

由于成像任务目标位置是基于地固坐标系进行描述的，而轨道要素转换的矢量信息是基于J2000历元平赤道地心坐标系的，需要进行坐标转换。从J2000坐标系到地固系的坐标系转换过程如式(8)～(12)所示，U为历元平赤道地心坐标系到瞬时平赤道地心系的转换矩阵，V为瞬时平赤道地心系到瞬时真赤道地心系的转换矩阵，W为瞬时真赤道地心系到准地固系的转换矩阵，S为准地固系到地固系的转换矩阵，Q为J2000坐标系到地固系的转换矩阵[8]。

U=Rz(-zA)Ry(θA)Rz(-ζA)

(8)

(9)

W=Rz(-SG)

(10)

S=Ry(-xp)Rx(-yp)

(11)

Q=S·W·V·U

(12)

所以地固系下相机视方向矢量为

a=Q·t

(13)

(14)

Re为地球赤道半径，Rp为地球极半径。联立单位矢量的空间直线方程与地球椭球方程得到

(15)

(16)

φ′=arctan (tanφ/(1-h)2)

(17)

本次计算获得的成像点地理经纬度(λ,φ′)，未考虑高程影响，需引入高程数据进行修正。由于现有高程模型数据点稀疏，为保证算法效率，选择以成像点为中心进行最近高程数据点线性插值，得到成像的高程数据b。使Re=Re+b,Rp=Rp+b,并重新代入式(14)进行计算，可得到使用高程模型数据修正后的成像点地固系位置，最终得到高程修正后的地理经纬度坐标。另外，对成像点的位置坐标进行微分，可得到卫星摄像点的移动速度，将分析结果与摄像点规划移动速度比较，可从任务角度间接反映姿态控制稳定性 。

1.4 算法精度

选某成像工况，将地面规划产生的卫星姿轨仿真数据带入算法，将成像条带位置计算结果与地面规划条带进行比较，得到的误差即为算法的计算误差。通过评估算法误差，对算法可信度进行评估。精度测试结果表明：算法计算得到的条带与地面规划的条带距离差保持在12 m以内，该误差远小于计算得到的条带实际执行误差(百米量级)。该比对结果说明：算法满足测试地面验证精度要求，可以投入卫星进行敏捷机动姿态控制精度验证分析使用。

2 地面测试验证应用示例

新型姿态品质评估方法已应用于某卫星的姿态敏捷机动测试验证工作，实现了密集成像姿态机动过程中姿态控制品质综合评估。选取第3轨道圈的某被动推扫工况的成像条带分析的典型曲线进行示例，图7为三轴姿态角变化曲线，由曲线可判断该工况有20个被动条带任务；图8为第15个被动推扫条带在地球表面推扫的轨迹;图9选取第15个推扫条带进行详细分析，分别从条带轨迹契合度、镜下点扫描速度以及镜下点地心角速度变化等方面进行分析；表1选取具备典型姿态机动角的7组条带进行姿态机动速度、成像时姿态稳定度分析。

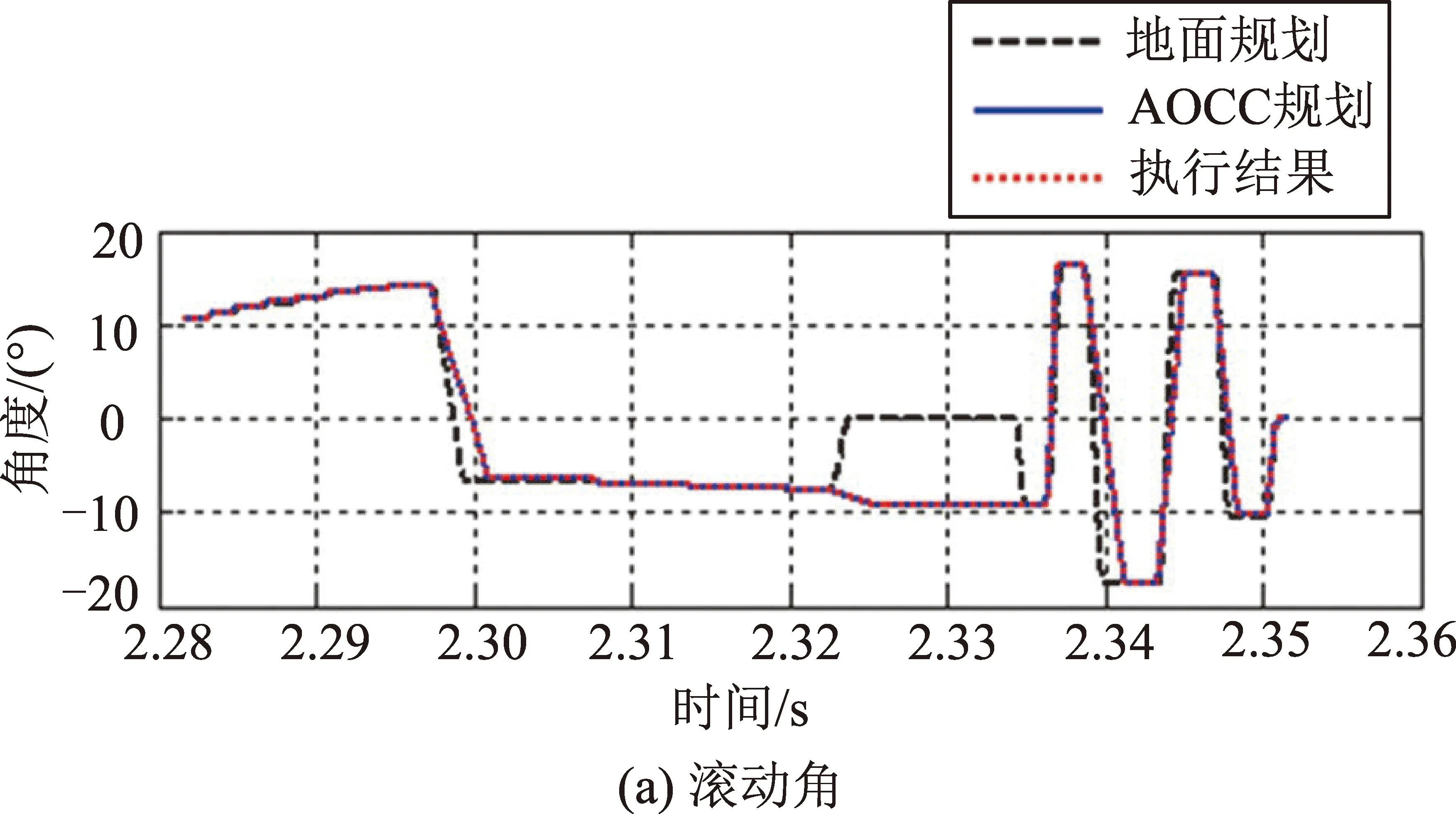
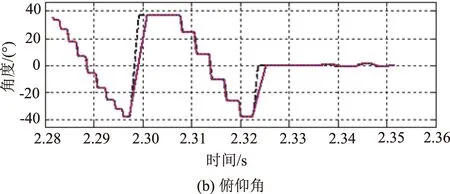
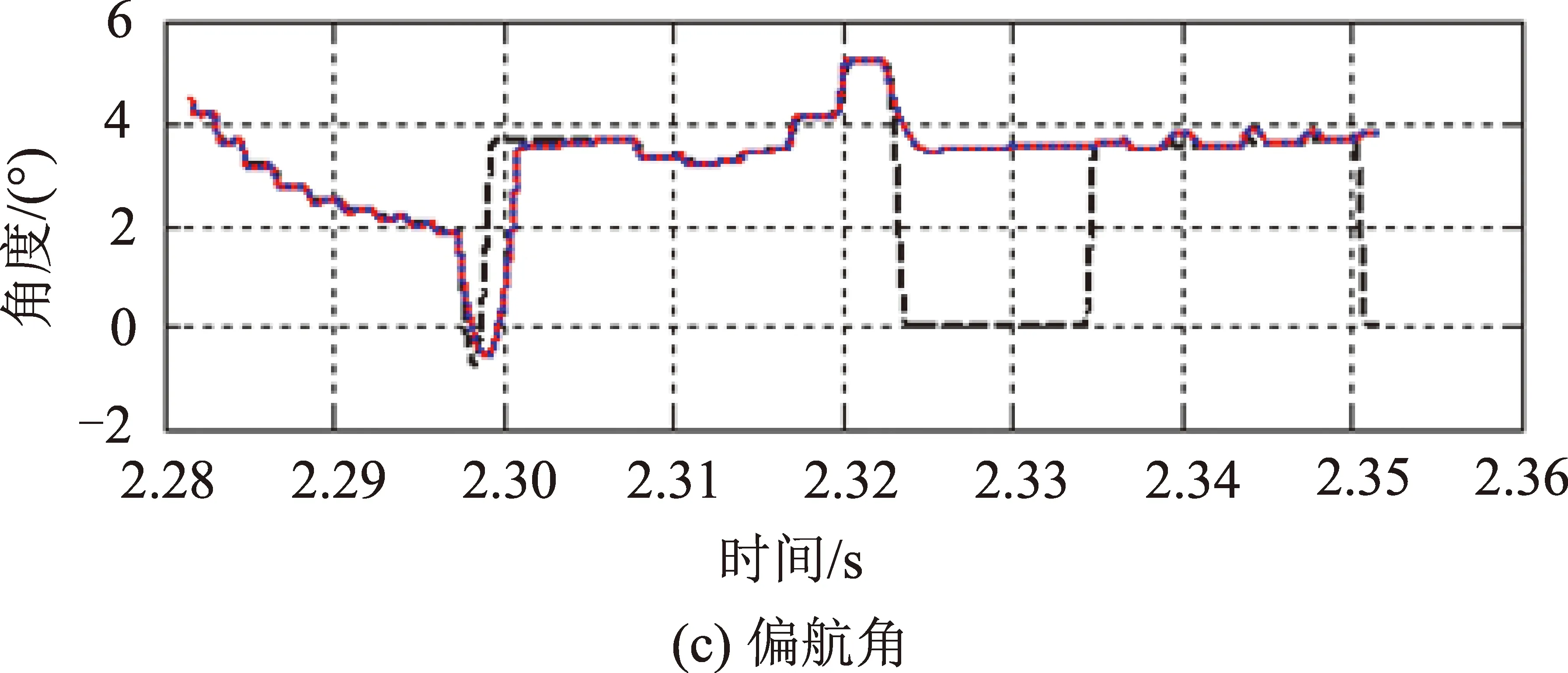
图7 三轴姿态执行情况比较

图8 执行与规划条带位置比较

表1 典型条带姿态指标分析

3 在轨应用思考

考虑相机在轨安装形变有可能使成像点位置偏移造成计算误差，因此需要考虑安装矩阵修正，以提高本算法在轨应用的适应性。形变矩阵K在式(7)中已提及，下面介绍其求解过程。

设计卫星进行一组无姿态机动的针对星下点成像，理论成像轨迹即为某时刻的星下点轨迹，求得该轨迹在地固系下坐标向量，标记为t0。实际成像点中心位置可根据图像分析确定，将图像中心点地理经纬度代入式(16)进行计算，获得实际成像条带在地固下坐标，标记为t1。由于t0及t1均为已知，在轨形变补偿矩阵K可根据式(17)、式(18)求得。

t0=M·K·[0,0,1]T

(18)

t1=Q·M·K·[0,0,1]T

(19)

由于求解过程是由实际成像结果以及卫星定轨数据通过数值求解得出，规避了复杂计算过程可能带来的误差，可以推断通过该方法求得的形变矩阵K，具备较高精度，也可用于在轨任务误差修正。

4 结束语

本文提出了一种基于成像点轨迹的敏捷机动姿态控制精度评估方法，将载荷成像点位置精度作为整星任务执行效果的评价指标，完善了敏捷卫星对地遥感载荷任务完成情况评估体系，并在模型中引入地表高程改进算法精度，进一步增强了算法在高原地区的适用性。该方法解决了当前新型敏捷卫星普遍面临的自主成像任务执行过程评估难题，提高了地面数据挖掘与深度分析能力。在敏捷类卫星飞速发展的大背景下，该评估方法存在更大实用价值。