保持平行关系中的重合特例

谢佳慧

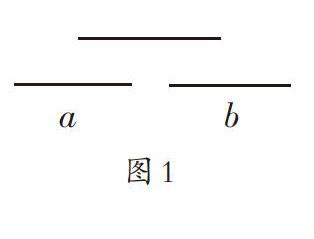
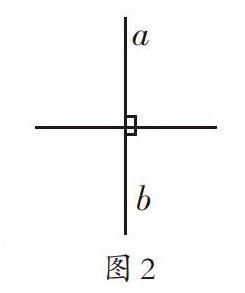
[摘要]保持平行关系是小学几何图形中常见的几何位置关系，但是对于保持平行关系概念的主体到底是线段还是直线并没有严格的界定，有时线段保持平行关系与直线保持平行关系的不同表述会使学生在理解上产生歧义。线段保持平行关系是指线段所在的直线保持平行关系，这样保持平行关系就存在一个重合问题，即两线重合算不算保持平行关系。

[关键词]平行关系;重合;质疑;反思

[中图分类号]G623.5 [文献标识码]A [文章编号] 1007—9068（2019）32—0030—01

一、精彩的质疑和求教

一天，有两个女生来找我评理，一个女生说：“老师，我觉得两根火柴棒这样子摆放（如图1的a和b）后，它们似乎不再保持平行关系了。”“可隔壁班的老师坚持说是保持平行关系的。”另一个女生不服气地说。

两个女生争论的问题源于人教版教材第七册第65页的第2题“摆一摆：（1）让两根火柴棒同时与第三根火柴棒保持平行关系，观察一下，这两根火柴棒能不能保持平行关系？（2）让两根火柴棒同时与第三根火柴棒垂直，看一看这两根火柴棒的位置关系如何”。这两个问题，前一个直接浅白，后一个复杂隐晦，难度逐步加大，思维含量高。我思考片刻，回复她们：“图1的摆法没有错，符合条件，别具一格。但是一旦出现这种情况，两根火柴棒就无法构成平行关系，这是一种特殊情况，严格来说，应该叫作两根火柴棒在同一直线上。”无独有偶，后来我在正式讲授第（2）题时，也有学生摆出异常的情况（如图2）。

图1和图2的情况不能认定为互相保持平行关系，但火柴棒作为有长度的木棍，可视为线段，出现这两种特殊情况情有可原。可教材没有正式提出“两条线段在同一直线上”这一空间定义，四年级的学生能不能无师自通、不言自明？要不要老师进行专题讲解？教了能否听懂？如果不讲解，在遇到上述特殊情况时如何处置？……一连串的问号出现在我的脑海里，久久无法解开。

二、争论后的反思

教材安排这两道题，其目的在于让学生通过操作、反思、辨析，总结归纳出两条推论：一是两直线同时与同一平面内另一条直线保持平行关系，那么这两直线也构成平行的位置关系;二是两条直线同时与同一平面内另一条直线垂直，那么这两条直线也构成平行的位置关系。因为这两条推论到了初中，就成为两条定理，可见这两条推论成为小学数学与中学数学的衔接桥梁。显而易见，课本编排这两道题，是科学合理的，是有着深远意义的。

教师首先要弄清直线与线段的异同：线段有两个端点，是截取直线的一部分而得到，其长度是具体可测的;而直线是没有端点限制的，其长度不受限，因此不可测。可以说，直线是由无数条线段无间隙连接而成。

三、反思后的实践探索

师：这两根火柴棒在几何学上属于线段还是直线？

生₁：线段。

师：若将图1中水平放置的两根火柴棒都视为直线，那么会有什么情况发生？这两条直线最终会有什么神奇变化？

生₂：与自身重叠了。

师：与自身重叠后，变成了几条直线？

生₃：合为一体，变成一条直线。

师：一条直线存在保持平行关系这一说吗？或者说直线能与自己保持平行关系吗？

生₄：不能。

师：那么两条直线同时平行于同一平面内的另一条直线，这两条直线如果没有重叠，会构成什么位置关系？

生₅：互相保持平行關系。

同理，两条直线同时垂直于同一平面内另一条直线，这两条直线如果不重合，会构成什么样的位置关系？有了前一题积累的经验和打下的基础，学生会立马认定：它们的位置关系是互相保持平行。在此基础上让学生练习巩固。如：（1）两根火柴棒同时与第三根火柴棒保持平行关系，观察一下，这两根火柴棒构成（ ）的位置关系;（2）两条线段同时垂直于同一平面内的另一条线段，判断一下，这两条线段构成（ ）的位置关系;（3）两条直线同时与同一平面内的另一条直线保持平行关系，那么，这两条直线构成的（ ）的位置关系;（4）两条直线同时垂直于同一平面内的另一条直线，那么，这两条直线（ ）。A.互相保持平行关系;B.互相保持垂直关系;C.互相保持平行关系或在同一直线上;D.无法判断。

笔者将反思所得应用于课堂教学，惊奇地发现，效果特别好，学生对于“两根火柴棒（线段）置于同一直线上”这一几何特性，均能够轻松掌握。特别是做过一组题目后，学生不但严格区分开了线段和直线，搞清了它们之间的异同，而且解决了上述两题，更为重要的是，为初中平行关系性质定理的学习打下了基础。

（责编 黄春香）