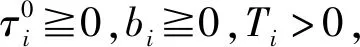新广义V-I致型多目标半无限规划ε-有效解的充分性

苏紫洋，王荣波

(延安大学 数学与计算机科学学院，陕西 延安 716000)

对于非光滑多目标规划的最优性条件的研究一直是近几年来的热点问题，并且取得了很大的成果，如文献[1-7]。在多目标规划问题中各种凸性及其推广也被广泛应用。例如，文献[2]将文献[1]引入的不变凸性理论推广为I型和II型不变凸性；文献[3]对文献[2]进行了进一步推广和应用；后来文献[4]推广了各种I型不变凸性，并提出了向量型不变凸性等相关概念，引入了V-I型、伪V-I型、拟V-I型等广义不变凸函数，并在这些广义I型的不变凸性条件下讨论了关于多目标规划的一些对偶性定理和最优性条件；文献[5]在对称可微的非光滑情况下把各种V-I型函数进行了推广，并给出了V-Is型等一些不变凸函数的定义；文献[6]在文献[5]的基础上定义了广义一致V-Is型等多个广义不变凸函数，且在广义一致V-Is型不变凸性条件下，讨论并得到了关于非光滑多目标半无限规划的一些最优条件。

本文借助文献[7]引入了新广义一致V-Is,ε型不变凸函数的概念。我们假设在新广义一致不变凸性的情况下，对一类非光滑多目标半无限规划问题进行了讨论和研究，并得出了若干个最优性结果。

1 基本概念

相关符号：

x∈Rn，y∈Rn，x≤y⟹xiyi∀i=1，…，n,x≠y。

x∈Rn,y∈Rn,xy⟹xiyi∀i=1，…，n,≥和≧分别与≤和≦的意义类似。

hi:R→R，hj:R→R，Ti:X0×X0→R+/{0}，Uj:X0×X0→R+/{0}，Z:X0×X0→Rn，

考虑下列多目标规划问题(SIVP)：

minf(x)=(f1(x),f2(x)，…，fi(x))T，

s.t.g(x,u)0,x∈X0⊂Rn,u∈U。

其中f:X0→Rp是对称可微函数，g:X0×U→Rm对于∀u∈U关于x是对称可微的，X0是一个开集，U∈Rm是一个无限参数集。

记：X={x∈X0|g(x,u)0,X0⊂Rn，u∈U}，

I(x*)={i|g(x*,uj)=0,x*∈X0,uj∈U}，

设U*={uj∈U|g(x,uj)0,j∈△,△是的任意可数子集}是U的任意可数子集，Λ={λj|λj0,j∈△，且仅有有限个λj≠0}。

定义1 设x*∈X，对ε>0，如果不存在x∈X，使得f(x)≤f(x*)-ε，则说x*是(SIVP)的ε-有效解。

定义2[6]设x∈X0如果存在一个Rn→Rn的线性算子fs(x)，使得对充分小的h∈Rn有

f(x+h)-f(x-h)=2hT·f(x)+α(x,h)‖h‖，

其中α(x,h)∈R1，且当‖h‖→0时，α(x,h)→0，则称f在x处对称可微，记为S-可微，称fs(x)为f在x处的对称梯度(当f为一元函数时，fs(x)称为对称导数)，如果f在每个x∈X0处对称可微，则称f在X0上对称可微。

定义3 对于问题(SIVP)，如果存在定义中的bi,bj,Ti,Uj,hi,hj使得

bi(x,x0)hi[fi(x)-fi(x0)]

∀x∈X0,i=1，…，p。

(1)

-bj(x,x0)hj(g(x0,uj))

Uj(x,x0)ZT(x,x0)gs(x0,uj)-ε，

∀x∈X0,j=1,…,m。

(2)

则称(SIVP)在x0∈X处是广义一致V-Is,ε型的。如果(SIVP)在每一点x∈X0处是广义一致伪V-Is,ε型的，则称(SIVP)在X0上是广义一致V-Is,ε型的；如果当x≠x0时不等式(1)为严格的，则称(SIVP)在x0处或X0上是广义一致半严格V-Is,ε型的。

定义4[6]对于问题(SIVP)，如果存在定义中的bi,bj,Ti,Uj,hi,hj，对一些τ∈Rp,τi0，λi∈Λ，使得

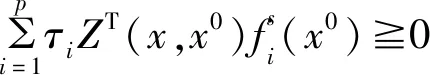
∀x∈X0,i=1，…，P。

(3)

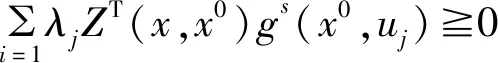
∀x∈X0,j=1,…,m。

(4)

则称(SIVP)在x0∈X处是广义一致伪V-Is型的。如果(SIVP)在每一点x∈X0处是广义一致伪V-Is型的，则称(SIVP)在X0上是广义一致伪V-Is型的；如果当不等式(3)(不等式(4))中的第二个不等式为严格的，则称(SIVP)在x0处或X0上是广义一致半严格伪V-Is型的；如果当不等式(3)和不等式(4)中的第二个不等式都为严格的，则称(SIVP)在x0处或X0上是广义一致严格伪V-Is型的。

定义5[6]对于问题(SIVP)，如果存在定义中的bi,bj,Ti,Uj,hi,hj，对一些τ∈Rp，τi0，λj∈Λ，使得

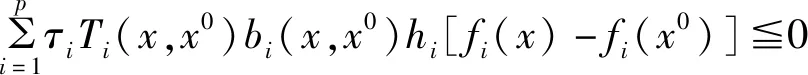
∀x∈X0,i=1，…，p。

(5)

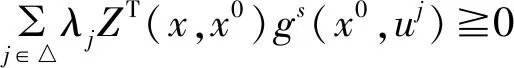
∀x∈X0,j=1，…，m。

(6)

则称(SIVP)在x0∈X处是广义一致拟伪型V-Is的。如果(SIVP)在每一点x∈X0处是广义一致V-Is型的，则称(SIVP)在X0上是广义一致拟伪V-Is型的；如果式(6)中的第2个不等式为严格的，则称(SIVP)在X0处或X0上是广义一致拟严格伪V-Is型。

2 充分性条件

定理1 假设x0∈X。如果：

(Ⅱ)(SIVP)关于bi>0，Ti>0，Uj>0，(j∈△)对于∀uj∈U*且在x0处是V-Is,ε型的。

(Ⅲ)当a<0时，hi(a)<-ε；当a0时，

hi(a)-ε；当a=0时，hi(a)=0。则x0是(SIVP)的ε-有效解。

证明由假设(Ⅱ)

bi(x,x0)hi[fi(x)-fi(x0)]

∀x∈X0,i=1，…，p。

-bj(x,x0)hj(g(x0,uj))

Uj(x,x0)ZT(x,x0)gs(x0,uj)-ε，

∀x∈X0,j=1，…,m。

上述两式相加得：

由(Ⅰ)得

(7)

通过(11)式可得：

(8)

由于bi>0,Ti>0,Uj>0，(j∈△)，(8)式也可表示为

(9)

定理2 假设x0∈X。如果

(Ⅱ)(SIVP)关于bi>0，Ti>0，Uj>0，(j∈△)对于∀uj∈U*且在x0处是广义一致拟严格伪V-Is型的。

(Ⅲ)当a<0时，hi(a)<-ε；当a0时，hi(a)-ε；当a=0时，hj(a)=0。则x0是(SIVP)的ε-有效解。

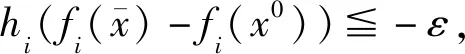
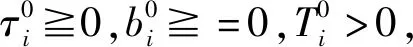
(10)

由假设条件(Ⅱ)得

上面两式相加得：

(11)

再有假设(Ⅰ)中的(a)得，

这与(11)式矛盾，故x0是(SIVP)的ε-有效解。

定理3 假设x0∈X。如果

(Ⅱ)(SIVP)关于bi>0，Ti>0,Uj>0,(j∈△)对于∀uj∈U*且在x0处是广义一致严格伪V-Is型的。

(Ⅲ)当a<0时，hj(a)<-ε；当a0时，hi(a)-ε；当a=0时，hj(a)=0。则x0是(SIVP)的ε—有效解。

由假设条件(Ⅱ)得：

由假设(Ⅰ)中的(a)得：

由假设(Ⅱ)得：

∀x∈X。

(12)