基于压缩感知的医学图像重建方法
2019-12-31张国平牟忠德
张国平,牟忠德
江苏省肿瘤医院,江苏省肿瘤防治研究所,南京医科大学附属肿瘤医院(南京,210009)
1 压缩感知
压缩感知基本构成通常包括稀疏表示、编码测量、重构算法等内容[1-3],其理论框架详见图1,该理论适合对信号的采样和编码,对原始的信号线性投影以后,获得测量信号值,然后通过重构算法,对该测量值进行重构,进而得到重建的信号[4-5]。
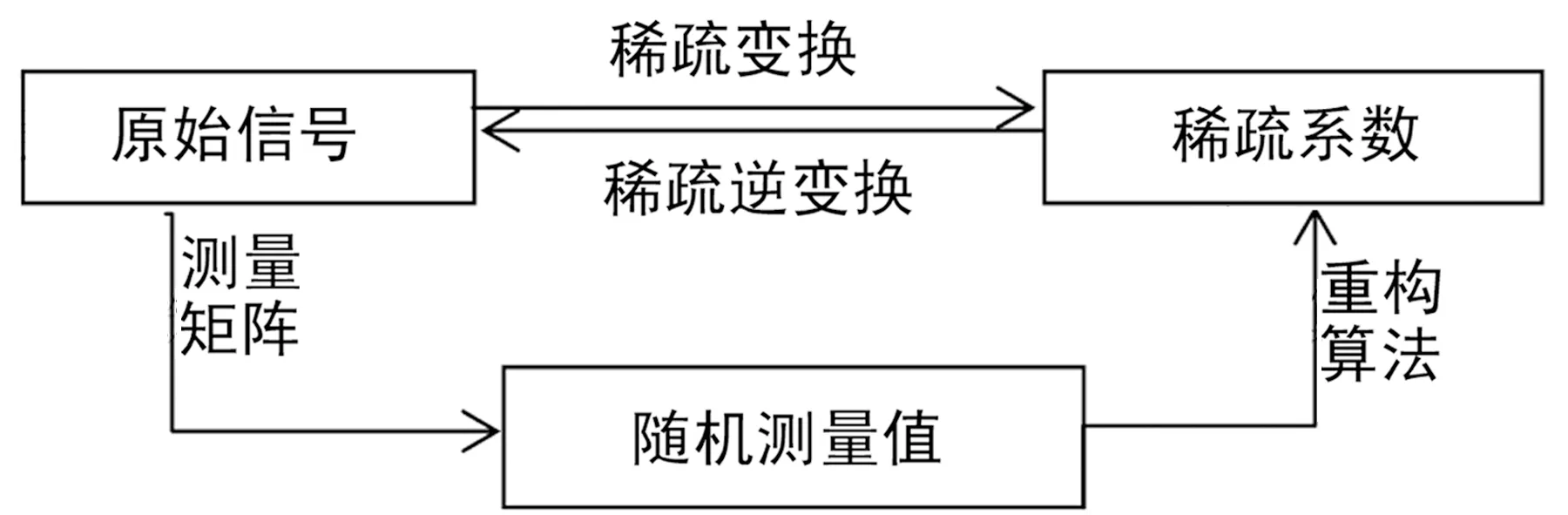
图1 压缩感知框架示意图
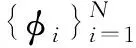
(1)
其中,φ表示对信号的稀疏变换域,Y表示信号X在φ域上的投影值。如果Y向量中只有K个系数,不为零或远大于其它的系数,则称X是K稀疏的,或者是可压缩的,即可得信号X的稀疏表达如式(2)[6-7]。
Y=φTX
(2)
2)根据压缩感知理论中的非相关性准则,使用矩阵ψ对信号Y进行观测,经式(3)可得测量矩阵。
S=ψφTX
(3)
3)假设Θ=ψφT,则有S=ΘX,最后在l0范数框架下优化求解X,结果如下:
min‖φTX‖0s.t.ΘX=S
(4)
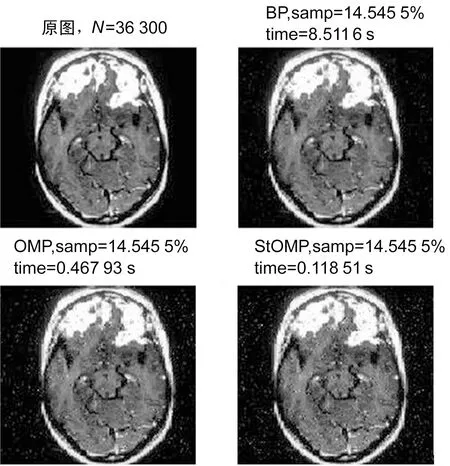
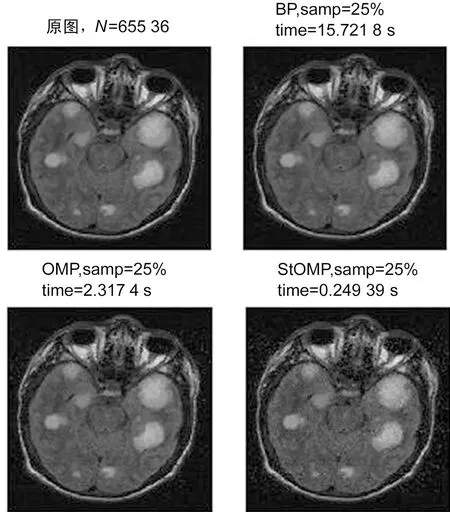
对于这个欠定方程(M 在压缩感知理论中,从稀疏系数中重构出原始信号就是信号的重构过程,重构算法可以转化为线性规划(Linear Programming,LP)问题的求解,直接求解方法即转换为求解最小l0范数问题[8-9]。 通过求解最小l0范数,来解决信号重构问题,即求解最小l0范数下的最优化问题,以求得最优化的重构结果,但是其计算复杂度较高。但是找到合适的稀疏信号,也就等于解决了式(4)的问题 (4) 其中,‖c‖0是序列{Ck}中非零项的个数。利用BP算法来解决式(5)的问题 (5) BP算法的求解过程中,原始信号记为x,φ,为观测矩阵,基矩阵φ已知,求解s等同于求解x,其中s,xRN,yRM,M OMP算法是基于匹配追踪算法的正交匹配追踪算法,来解决信号重构问题[10-12],该算法的具体步骤如下: 1)寻找残值r和矩阵ψj积中的最大元素的索引λ; 2)将索引集更新,记录经由传感矩阵φ进行重构后的原子集合,详细表示方式如下: Λt=Λt-1∪{λt} (6) φt=[φt-1,ψλt] (7) 3)实现式(8)中的最小二乘法; (8) 4)借助式(9),更新残值,t=t+1; (9) 5)对Step 4中t进行判断,满足条件t>K,则迭代停止;如果不满足,则继续执行步骤 1。 StOMP算法是由Donoho等对正交匹配算法进行改进,并提出了分段正交匹配追踪算法,该算法在正交匹配追踪算法的基础上做了简化[13-14]。StOMP算法具体步骤如下: 1)对数值进行初始化设置,设定最大的迭代步长,求解最大的迭代误差e,s=1; 2)将小波变换后,获得的变换系数,记为稀疏矩阵y,然后随机选取测量数据,得式(10): Θs=φTrs-1 (10) 3)对Θ进行如式(11)的规范化处理,其中K为Θ信号的长度 (11) 4)对Θ进行阈值处理,如式(12): ∑S={j:|ΘS(j)|>λS} (12) 5)最新合并两次变换所得的坐标索引,并对IS集合进行一致化处理如式(13),得IS: IS=IS-1∪ ∑S (13) 6)求解线性方程组,min(‖xs‖1)s.t.y=φXS,计算公式如(14)。 (14) 7)计算残差rS,如式(15): rs=y-sS (15) 8)稀疏解的精度判定,如rs 为了比较不同的压缩感知图像重构算法,我们选择Shepp Logan模型来作为测试图像,对其取Haar小波变换并进行仿真实验,分别采用BP算法、OMP算法、StOMP算法进行图像重构,在相同的采样频率下,比较其重构时间和重构效果如图2所示。 图2 采样率为10%的Shepp Logan重构结果 为比较不同采样频率,在实际的临床MRI医学图像条件下,观察压缩感知算法的重建效果,在欠采样率为10%-50%范围内,分别选择15%和25%两种采样情形下,观察这三种算法对实际的临床MRI医学图像的重构效果如图3和图4所示。 综上所述,可以得到如下结论:(1)借助压缩感知理论,通过合理的算法设计,是可以近似重构出医学图像的,并且整体图像质量不会明显下降。(2)在相同欠采样率的情况下,BP算法的重构结果是最好的,但运算时间最长;OMP算法的重构结果次之,是运算时间比BP算法少;StOMP结果最差,不适用于精确的图像重建。 图3 采样率15%的MRI重构结果 图4 采样率25%的MRI-Brain重构结果2 重构算法分析
2.1 BP算法
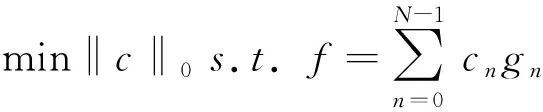
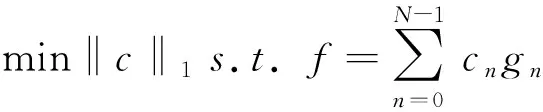
2.2 OMP算法
2.3 StOMP算法
3 实验结果与分析
3.1 使用Shepp Logan的实验结果
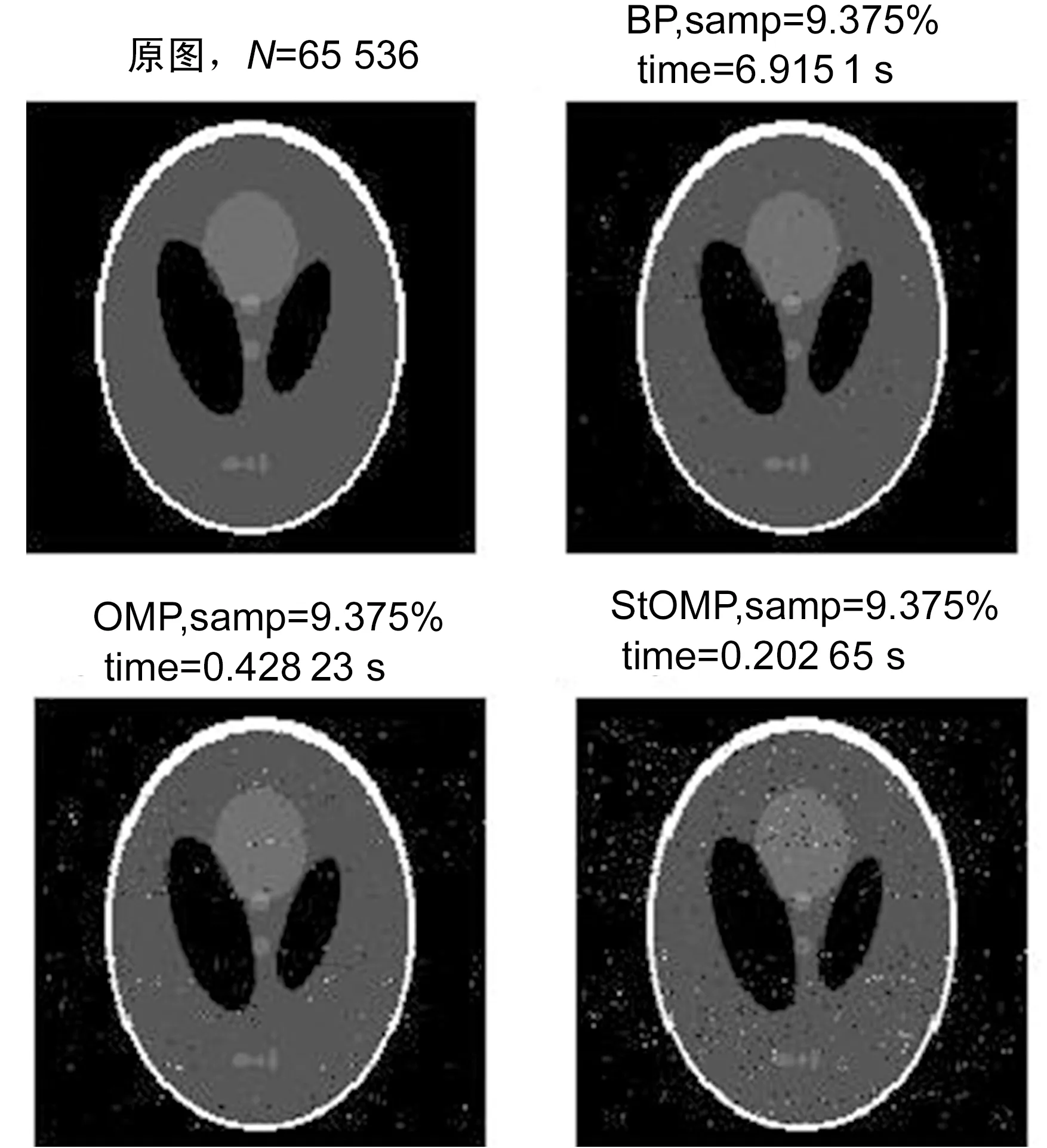
3.2 使用真实MRI图像的实验结果
4 结论