磨削过程信号监测与砂轮磨损预测模型构建

郭维诚，李蓓智，杨建国，周勤之

(东华大学 机械工程学院，上海 201620)

磨削为加工过程的的最后一道工序，广泛应用于对产品尺寸精度和表面粗糙度有较高要求的生产场合.在磨削过程中，砂轮磨损会使磨粒钝化而逐渐失去切削能力，导致零件的表面质量下降，同时产生磨削烧伤和颤振[1-4].因此，需要对砂轮磨损进行实时和有效地监测，以防止零件质量的恶化.当磨损严重时，系统将监测结果及时通知加工设备或者操作人员，为砂轮修整提供决策依据，确保加工质量和效率.

国内外学者采用直接和间接监测两种方法对砂轮磨损进行了大量的研究.直接监测方法使用光学显微镜和CCD摄像机获取磨削加工后砂轮的表面形貌或轮廓特征，利用图像处理算法得到磨粒高度或砂轮直径的变化量，以此评估砂轮的磨损程度[5-7].虽然显微镜和摄像机可以直观地了解砂轮的工作状况，但在实际加工过程中，这种方法需要机床停机，并通过一定的方式夹持测量设备进行拍摄和处理，时间成本较高且影响砂轮加工效率.

砂轮磨损的间接监测方法建立磨削过程的物理量如力、热、振动和声音等与砂轮磨损的关系，通过观察这些物理量的变化，间接地了解砂轮的磨损情况.研究表明，磨削力、加速度以及声发射信号有效值和声发射小波包能量等信号特征与砂轮磨损的变化趋势基本一致[8-12]，能够有效地反映砂轮的磨损状况.随着机器学习方法在机械加工领域不断应用，砂轮磨损的间接监测从传统的经验数值模型转变为基于数据驱动的智能模型，神经网络和支持向量机等智能算法在很大程度上提高了磨损预测结果的准确性[13-16].

建立砂轮磨损预测模型的过程中，大部分研究在选取输入特征时并未采用系统化的选择方法，而是根据经验知识选择一些常用的信号特征.然而，这些特征可能与砂轮磨损并不相关.本文开展了外圆纵向磨削实验，对功率，加速度和声发射信号进行预处理，并提取出这些信号中的时域和频域特征，利用基于多特征优化融合的随机森林(MFOF-RF)算法选择与砂轮磨损相关性较高的特征，并建立砂轮磨损预测模型.实验得到的训练样本用于确定模型的最优参数和特征组合，测试样本用于评估模型的预测能力.

1 磨削实验设计与砂轮磨损测量

磨削实验使用型号为MGKS1332/H-SB-04的高速外圆磨床，砂轮主轴的最高转速为150 m/s，主轴功率为37 kW，并配有SBS主轴动平衡仪.实验采用棕刚玉砂轮，直径为400 mm，宽度为20 mm，粒度号为46.工件牌号为42CrMo，直径和长度分别为45和200 mm，经过热处理后工件的硬度大约为HRC 40.

实验工艺参数为：砂轮线速度28 m/s，工件线速度0.37 m/s，切深15 μm，纵向进给率为2 mm/r.实验前，需要对砂轮进行修整，使磨粒锋利，恢复磨削性能，将修整后的砂轮定义为新砂轮.

如图1所示，在实验过程中，磨削功率和振动分别通过连接至主轴电机的功率传感器PH-3和安装在尾座上的三向加速度传感器KD1010LS采集而得，采样频率为5 kHz，用1个频率响应范围为 100～1 000 kHz的声发射传感器WG-50探测磨削过程中因材料去除而产生的应力波，采样频率为 3 MHz.

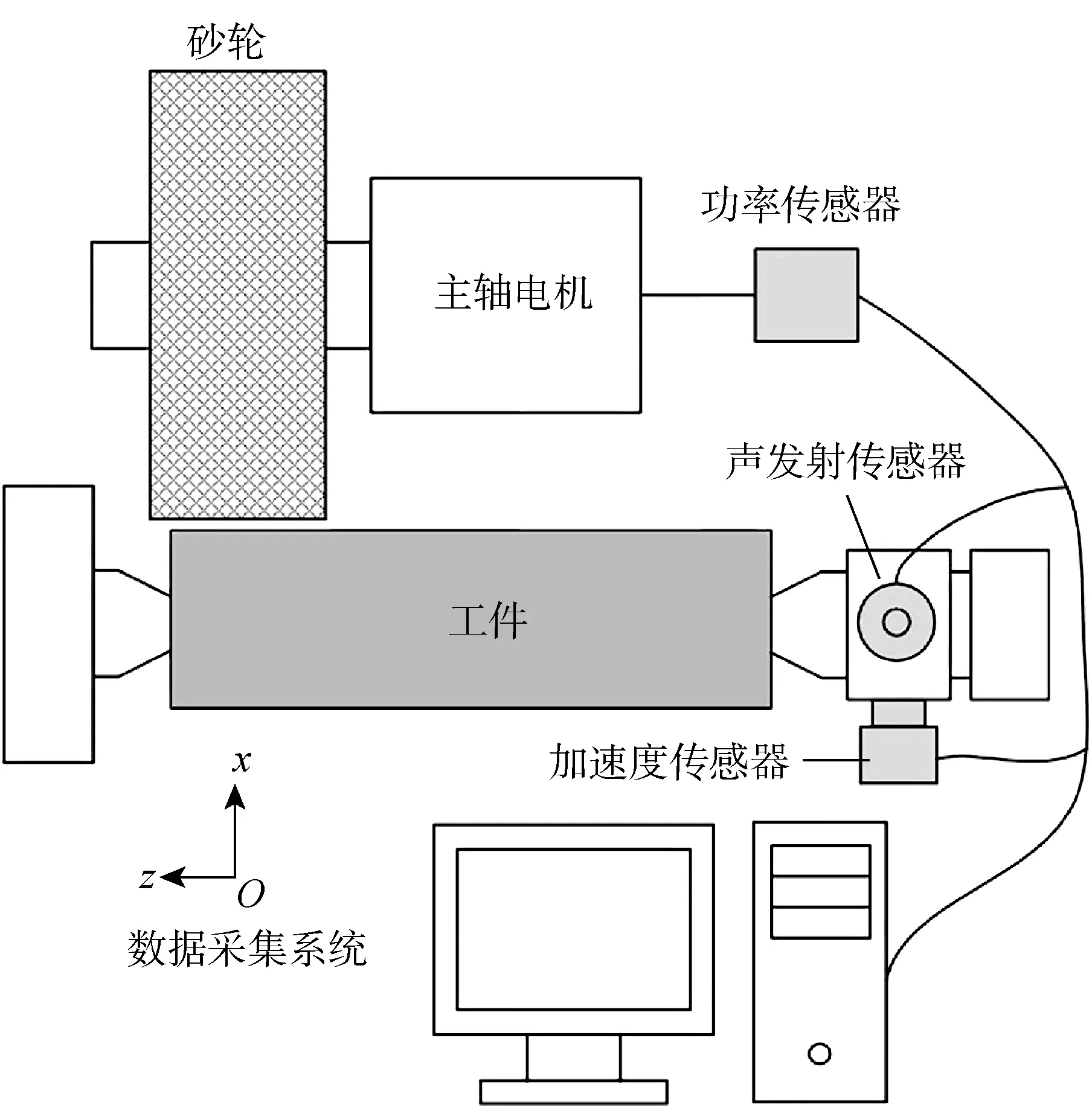
图1 砂轮磨损装置示意图Fig.1 Schematic diagram of wheel wear experiment setup

砂轮磨损的评价标准较多，在外圆切入磨削和平面磨削中，一般通过对比砂轮参与和未参与磨削的部分，计算砂轮的径向磨损量[17].而在外圆纵向磨削中，砂轮整体参与磨削，无法找到一个参照标准对比得到砂轮的磨损量，因此可以利用砂轮的表面形貌参数如磨粒密度、磨粒尖锐度以及磨粒高度等评价砂轮的磨损程度[18-20].一个刚修整完的砂轮磨粒尖锐，磨粒高度较高.经过一段时间磨削后，磨粒在摩擦和挤压作用下，棱角逐渐变钝或破碎，磨粒高度随之下降.本文使用磨粒高度均值作为砂轮磨损的评价指标，计算公式为

(1)

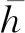
实验过程中，每经过2 000 mm3的材料去除量后，使用Keyence LK-H020激光位移传感器(测量范围(20±3) mm，精度±0.1 μm)随机测量砂轮表面沿z方向上5个不同区域的磨粒高度(H)，通过计算机对5次测量结果取平均值，得到砂轮表面磨粒高度均值，如图2所示.

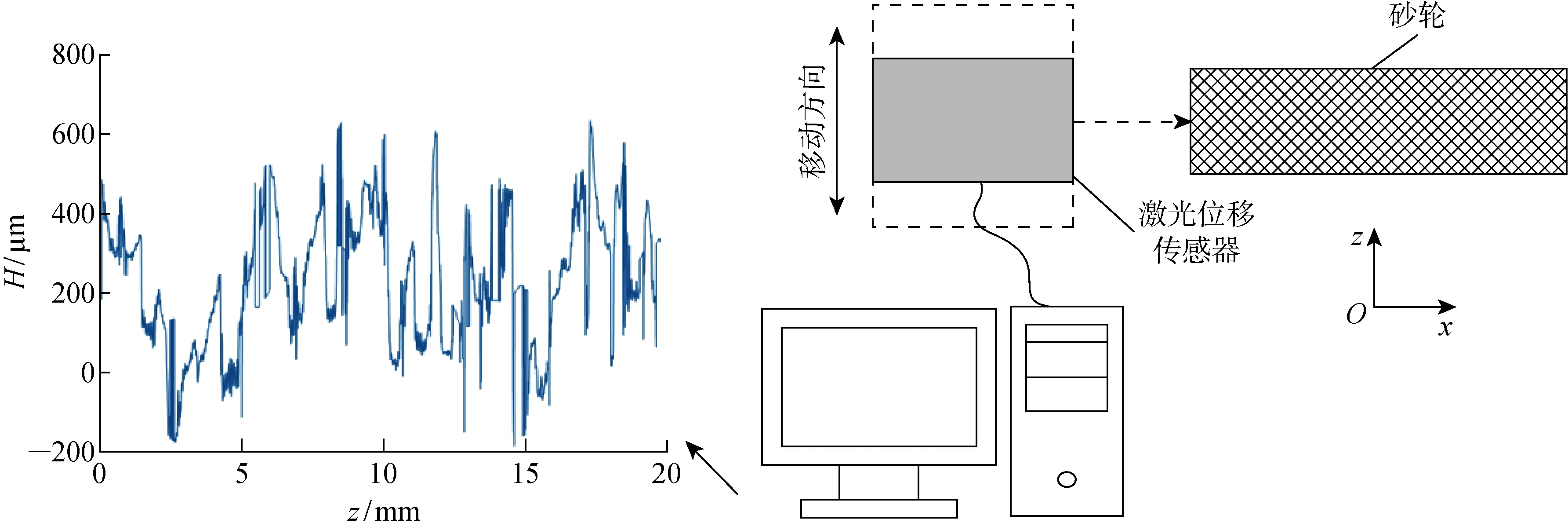
图2 砂轮磨损的测量过程Fig.2 Measurement process of wheel wear

2 砂轮磨损预测方法

2.1 信号预处理

信号预处理包括滤波和降采样，前者消除信号中的高频噪声，并使降采样过程中信号的频谱向外扩展时不会产生混叠；后者对信号进行抽取，减小数据量，提高特征提取与选择的效率.

功率传感器通过采集磨削过程中主轴电机的电压和电流，计算得到磨削功率.由于电压与电流的工频为50 Hz，所以对于功率信号采用了1个截止频率为100 Hz的Butterworth低通滤波器进行预处理，降采样频率为200 Hz.

磨削振动包括由机械部件产生的自由振动、外部激振力作用产生的强迫振动以及磨削力引起的自激振动[21].根据实验使用的磨削参数和磨床的机械特性，对实际频率2 kHz以内的三向加速度信号分别使用了不同带宽(50，100，…，500 Hz)的Butterworth带通滤波器以及4 kHz的降采样频率.

磨削时材料的塑性变形和断裂会释放应力波，声发射传感器通过检测这种能量来判断磨削状况.对于一般的金属切削，声发射信号通常在数百千赫兹的频率范围内传播.与加速度信号的预处理相同，对实际频率为100～1 000 kHz的声发射信号分别使用了不同带宽的Butterworth带通滤波器，降采样频率为 2 MHz.磨削功率，加速度和声发射信号的预处理参数见表1.

表1 不同磨削信号的预处理参数Tab.1 Preprocessing parameters for various grinding signals

2.2 特征提取

由于功率信号的频率范围较低，其频域特征意义不大，因此对预处理后0～100 Hz的功率信号提取时域特征，包括：平均值、有效值、标准差、峰度、峭度、峰峰值以及波峰因数等7个特征.

对于每个带宽中的三向加速度信号，除了提取与功率信号中相同的7个时域特征外，还利用Welch方法计算出该带宽中信号的功率谱密度(PSD)，获得PSD的平均值、标准差、峰度、峭度、峰值、峰值频率、波峰因数，以及频率质心、频率质心惯量和PSD熵10个频域特征.

声发射信号具有瞬态性和多态性的特点，其时域和频域特征与一般的信号特征有所不同.在声发射信号的每个带宽频率内，提取出上升时间、振铃计数、峰值计数、能量、持续时间、幅值、有效值、平均信号水平、信号强度和绝对能量10个时域特征，并通过傅里叶变换得到起始频率、混响频率、平均频率、频率质心和峰值频率5个频域特征.

2.3 特征选择

虽然从功率、加速度和声发射信号中可以提取出上百个特征，但并非每个特征的变化趋势都与砂轮磨损相关.因此，需要依照科学的选择方法，找到与砂轮磨损高度相关的特征，以此建立准确、可靠的预测模型.决定系数(R2)用于表示自变量与因变量之间的依赖关系[22]，若将信号特征作为自变量、砂轮磨损作为因变量，即可用R2评估信号特征与砂轮磨损的关联程度.R2可以通过以下公式计算：

R2=1-Sres/Stot

(2)

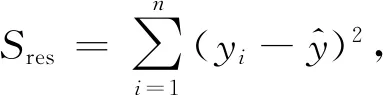
2.4 随机森林

随机森林(Random Forest，RF)是一种集合学习方法[23]，通过在训练时构建大量的决策树，获得由投票机制决定的决策树输出类别或所有单颗决策树的平均预测值.随机森林对数据和特征进行随机化有放回地抽样，构建多棵分类树，再根据结合策略进行整合得到最终的结果.利用随机森林进行回归预测的过程如图3所示，具体包括4个步骤：

(1) 若信号s的样本大小为N，对于每棵决策树采用自助法随机且有放回地从训练集中抽取k个自助样本集，作为新训练集，并由此构建k棵决策树；

(2) 每个自助样本集的信号特征数量为D，随机选择d个特征(d≪D)作为决策树节点分裂的候选特征；

(3) 每棵决策树的节点不进行剪枝，以达到最大的分裂深度；

(4) 将所有决策树组成随机森林，以每棵树预测结果总和的平均值作为随机森林的最终预测结果.

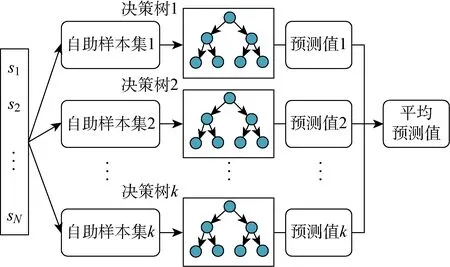
图3 随机森林算法过程Fig.3 Process of random forest algorithm

随机森林中的每1颗决策树作为独立的学习模型进行线性组合后，其方差比组合中任意单个模型的方差小.在进行方差缩减时，选择了许多复杂而具有较小偏差的强学习模型.由于每一个学习模型都与之前的模型独立，因此随机森林可以有效降低预测变量中的噪声.

2.5 MFOF-RF算法预测砂轮磨损

多特征优化融合是指利用多种传感器检测磨削产生的物理信息，包括力、热、振动和声音等，使用不同的信号处理方法从时域和频域中提取多个信号特征，并依据一定的评价标准进行特征选择，通过不同特征的优化互补，从而可靠地反映砂轮的磨损状态.

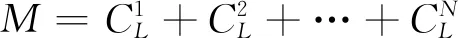
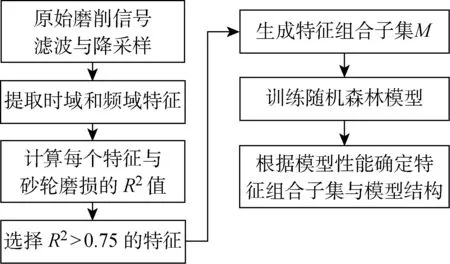
图4 基于MFOF-RF的砂轮磨损预测流程图Fig.4 Flowchart of wheel wear prediction using MFOF-RF algorithm

3 实验结果

3.1 特征选择结果与数据处理

经过对磨削功率、加速度和和声发射信号的预处理、特征提取以及特征选择后，功率有效值、功率平均值、声发射有效值、声发射平均信号水平和声发射能量等5个特征的R2大于0.75，因此将这5个特征作为输入变量建立砂轮磨损预测模型，预处理参数和R2值见表2.

在训练预测模型前，需要对输入变量(信号特征)和输出变量(砂轮磨损)进行归一化处理，以防止训练过程中出现单一特征占主导地位或过拟合的问题.各个磨削信号特征的数值差异很大，例如功率平均值可达上百瓦，而声发射有效值仅有几微伏，因此，将每个信号特征的数值与其初始值的比值作为归一化后的特征值，则所有的信号特征值被压缩至相同的数量等级内，并且均从1开始，表示特征值从新砂轮开始变化.归一化后的功率有效值、功率平均值、声发射有效值、声发射平均信号水平和声发射能量5个特征如图5所示，图中V为材料去除量.

为了使砂轮磨损的变化更为直观，采用最小最大值归一化方法，将磨粒高度均值转化为从0开始递增的磨损程度：

表2 与砂轮磨损相关性较高的特征及其预处理参数Tab.2 Features highly related to wheel wear and their preprocessing parameters

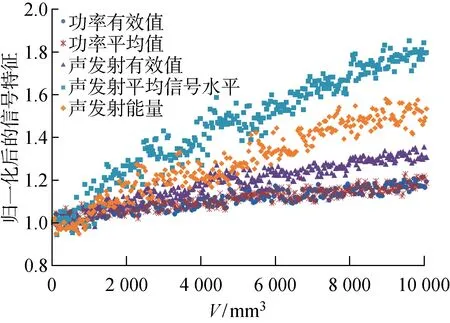
图5 信号特征的归一化Fig.5 Normalization of signal features

(3)

式中：W为归一化后的砂轮磨损程度；Hgmax和Hgmin分别为测量得到的最大和最小磨粒高度均值.实验中测量得到的磨粒高度均值和归一化后的砂轮磨损程度如图6所示.

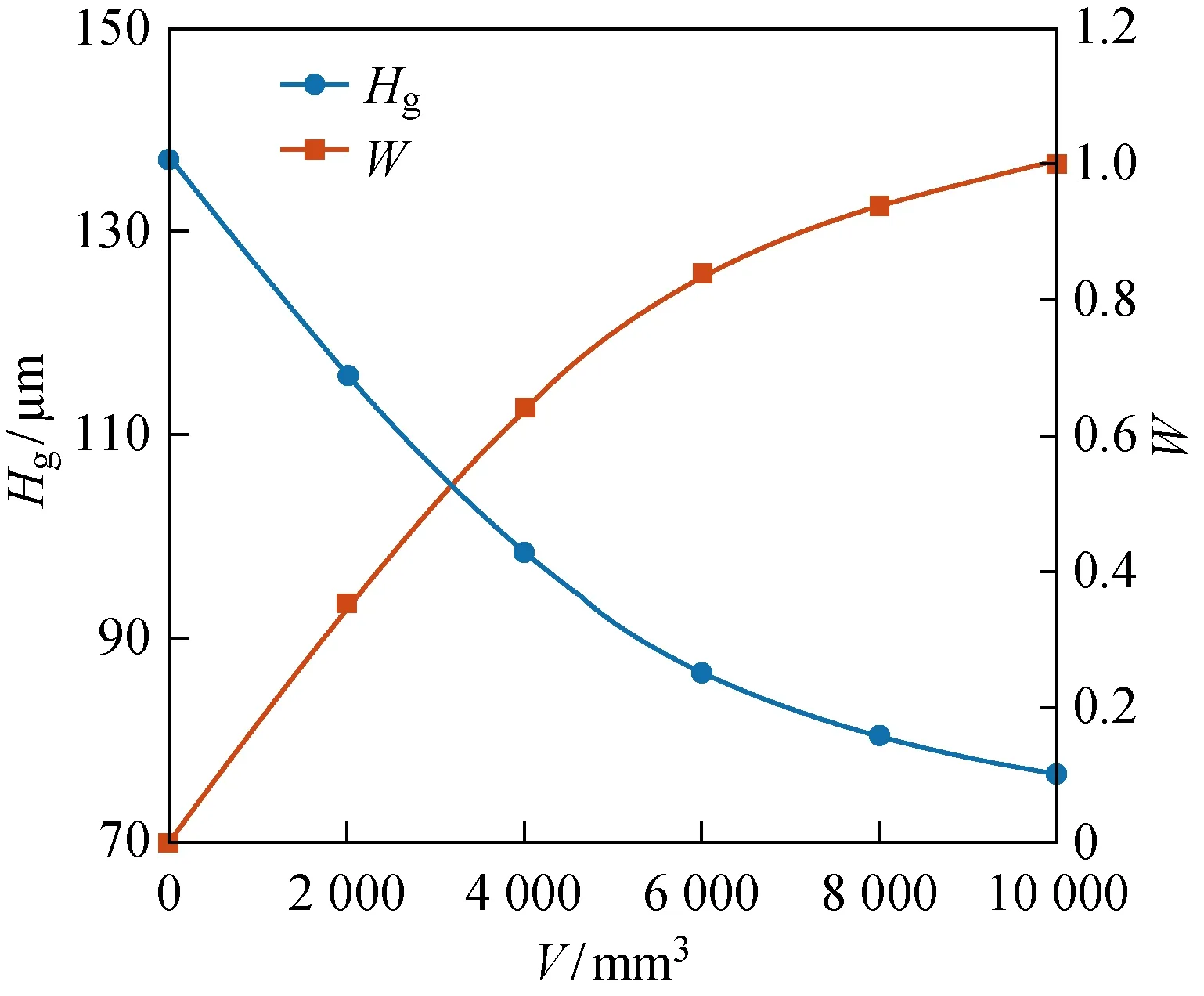
图6 磨粒高度均值的测量结果与砂轮磨损程度的归一化Fig.6 Measurement results of average grit height and normalization of wheel wear degree

3.2 砂轮磨损预测模型的训练与验证

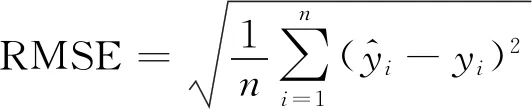
决策树棵数是随机森林模型的基本参数，直接影响模型的预测效果.图7为使用训练样本中的5个信号特征后，模型性能随决策树棵数的变化规律.当决策树的棵数大于100时，模型的R2和RMSE趋于稳定.因此，选择100棵决策树作为随机森林模型的最优参数.

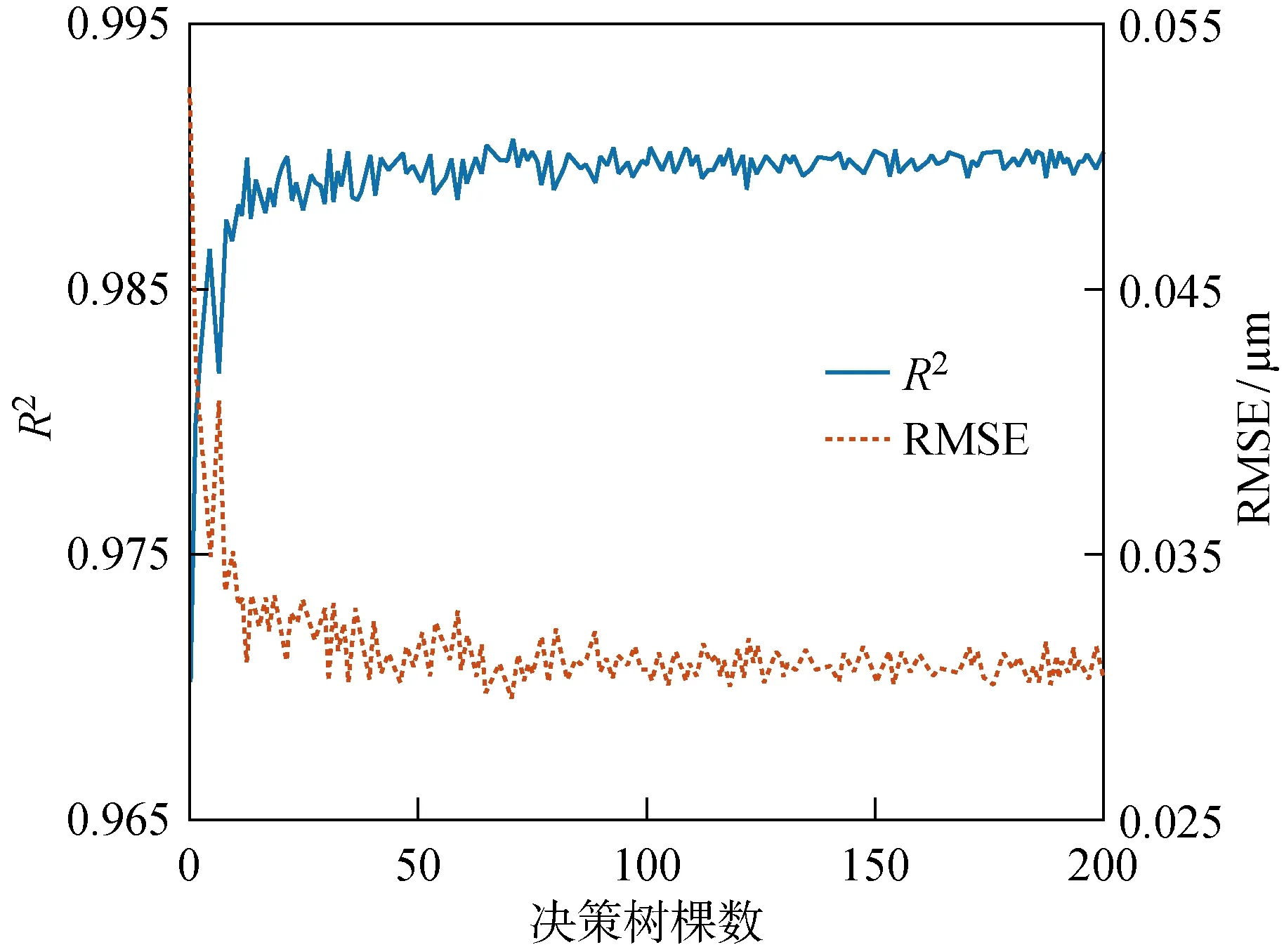
图7 决策树棵数对模型性能的影响Fig.7 The effect of number of trees on the model performance

一般情况下，输入特征的数量越多，模型的训练效果越好，预测精度越高.但如果某些特征训练样本存在较大的噪声，即使它们与砂轮磨损的相关性较高，也会降低模型的预测能力.因此，在模型训练前，需要将所选的5个特征进行组合，评估不同的特征组合子集对于模型预测结果的影响.

不同特征组合下预测模型最佳的R2和RMSE如图8所示.可以看出，当D小于5个时，模型的性能随着D增加而提高；而使用全部5个特征后，模型的R2和RMSE略有下降.因此，本文选用4个特征作为随机森林模型训练的输入，特征组合为功率有效值、功率平均值、声发射有效值和声发射平均信号水平，模型的R2和RMSE分别为0.991和0.03.

利用测试样本验证训练后的模型，砂轮磨损的预测结果如图9所示.通过观察模型的R2和RMSE可知，相比训练阶段，模型在验证阶段的预测能力有所下降，但其变化规律基本不变.对比使用单个输入特征的模型预测能力，采用4个特征融合时模型的R2和RMSE分别从0.937和0.075提高至0.977和0.046.因此，选择功率有效值、功率平均值、声发射有效值和声发射平均信号水平作为随机森林模型的输入变量可以更准确地预测砂轮磨损的变化情况.

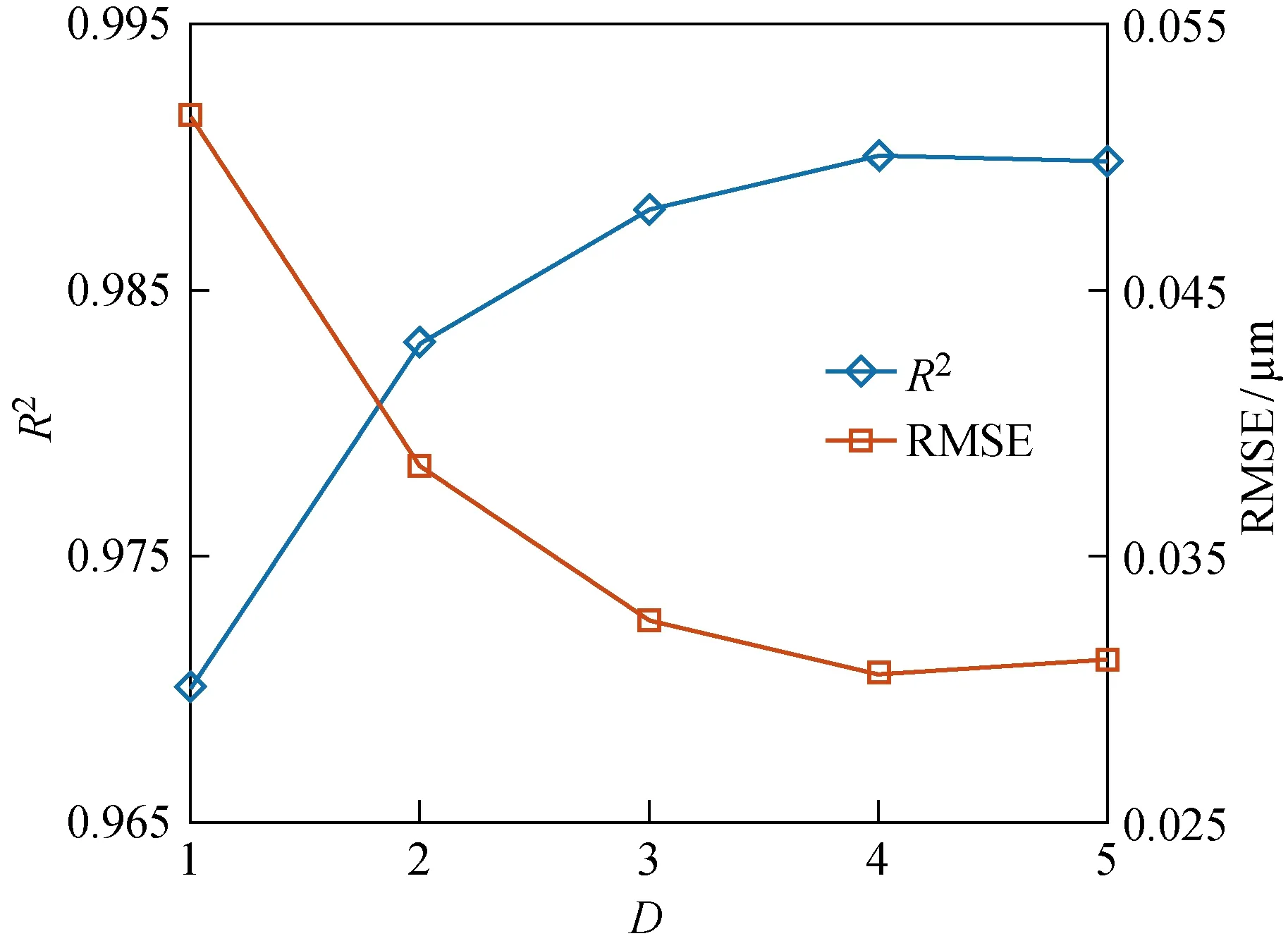
图8 特征数量对模型性能的影响Fig.8 The effect of number of features on the model performance

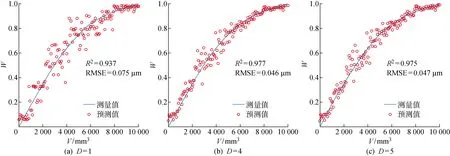
图9 不同特征数量下预测模型的验证结果Fig.9 Validation results of the prediction model with different numbers of features using testing data

4 结论

本文开展了外圆纵向磨削实验，提出了基于多特征优化融合的随机森林算法，利用磨削信号特征预测了砂轮磨损的变化情况，主要结论如下：

(1) 通过对磨削功率、加速度和声发射信号进行预处理和特征提取，获得了大量的时域和频域信号特征，并以R2为指标，从中选择了功率有效值、功率平均值、声发射有效值、声发射平均信号水平和声发射能量等5个与砂轮磨损相关度较高的特征.

(2) 以R2和RMSE评价砂轮磨损预测模型的性能，使用100棵决策树以及功率有效值、功率平均值、声发射有效值和声发射平均信号水平等4个特征训练模型，获得了最好的预测结果，模型的R2和RMSE分别为0.991和0.03 μm.

(3) 模型在验证阶段的预测性能略有下降，但依然能够准确地预测砂轮的磨损状况.相比于利用单个特征作为输入变量建模，MFOF-RF模型使信号特征与砂轮磨损的相关程度从0.937提高至0.977，预测误差降低了38.7%.