路面随机激励下康复机器人轮椅的抑振解析

赵雷雷，于曰伟，周长城，杨福兴

(1. 山东理工大学 交通与车辆工程学院，山东 淄博 255049；2. 北京邮电大学 自动化学院，北京 100876)

康复机器人轮椅属于康复医疗机械，为康复病人进行身体锻炼和参与社会活动提供了便利[1-2].随着社会的发展，机器人轮椅使用者的出行需求在不断增大[3].机器人轮椅在行进过程中，路面不平顺随机激励导致的人体振动不可避免，对病人的康复和舒适性产生了不利影响[4].因此，如何有效降低机器人轮椅的振动引起了人们的极大关注.

近年来，国内外学者围绕机器人轮椅的振动及舒适性问题展开了相关研究，但尚未给出抑制人体-机器人轮椅系统在路面不平顺随机激励下振动的解析优化数学模型.文献[5]对轮椅坐垫阻尼特性进行了研究，但未给出阻尼特性的匹配方法；文献[6]为了便于轮椅减振系统设计，提出了两段连杆式人体振动模型；文献[7]分析了行进过程中轮椅的振动传递特性及对病人的影响，但并未提出有效的振动抑制方法.文献[8]基于人体-轮椅6自由度模型对轮椅在正弦激励下人体振动进行了仿真，但对机器人轮椅随机振动没有详细研究，更未给出相应的抑制措施.文献[9]基于Q-Learning算法提出了一种新的机器人轮椅使用者舒适性评价方法，这对机器人轮椅的振动及舒适性评价具有一定的参考价值，但未给出机器人轮椅抑振优化模型及方法.文献[10]建立了电动轮椅坐垫舒适度数学模型，为轮椅设计提供了参考，但未提出坐垫减振特性匹配方法.由此可见，人体-机器人轮椅系统在路面不平顺随机激励下的振动抑制方法有待进一步研究.

为了有效抑制人体-机器人轮椅系统的振动，本文以不平顺随机路面作为机器人轮椅典型行驶路况，建立人体-机器人轮椅垂向振动模型；探究路面不平顺随机激励下人体-机器人轮椅系统的振动响应特性，进而创建人体-机器人轮椅抑振参数的解析优化模型及方法.

1 人体-机器人轮椅垂向振动模型

对于康复机器人轮椅，若建立复杂的振动模型进行振动分析，不仅需要大量的处理工作，而且在机器人轮椅的设计初期，建立精确振动模型所需要的参数常常是未知的.因此，需要对机器人轮椅进行简化，以便快速地对轮胎、坐垫等减振元件的设计参数作出合理的选择，避免反复试验，从而降低研发成本.路面激励对人体影响较大的振动主要集中在1.0～10.0 Hz.人体是一个复杂的振动系统，为了便于理论计算，将人体视为刚体质量并忽略机器人轮椅的几何特征，创建人体-机器人轮椅垂向振动模型，如图1所示.在该模型中，将坐垫及轮胎均简化为具有线性刚度和阻尼的减振元件.图1中：m1和m2分别为椅身质量和人体质量；K1和C1分别为所有轮胎的总垂向刚度和总阻尼；K2和C2分别为坐垫刚度和阻尼；z1和z2分别为椅身质量和人体质量相对于各自静平衡位置的垂向位移；q为路面高程.轮胎及坐垫主要隔离垂向振动，故本文仅对人体-机器人轮椅的垂向振动进行分析.

图1 人体-机器人轮椅垂向振动模型Fig.1 Vertical vibration model of human-wheelchair

根据牛顿第二定律，可得上述模型的振动微分方程为

(1)

机器人轮椅常在人行道上行驶，其路面形式有水泥、沥青及铺砖等.不同路面的铺装形式对机器人轮椅通行的影响主要通过路面形成的激振频率来完成.当机器人轮椅在沥青或水泥等随机路面上行驶时，可将路面谱抽象为满足一定条件的白噪声，其时域模型为[11]

(2)

上述随机路面模型的速度功率谱密度可表示为

(3)

式中：ω=2πf且f为激振频率.

2 振动响应解析式

幅频特性分析能直观地呈现振动系统在不同频率下的减振性能，加速度方均根分析可用于整体减振性能评估[12-13].为此，本节基于人体-机器人轮椅垂向振动模型，推导了人体振动加速度频响函数及方均根解析式，并提出了振动响应系数，进而实现振动响应的解析描述.

2.1 人体振动加速度频响函数

仅讨论人体-机器人轮椅系统的质量、刚度及阻尼参数，只能对特定的康复机器人轮椅进行振动分析和设计.因此，为了使讨论的物理量具有更广泛的理论指导意义，引入以下辅助变量：

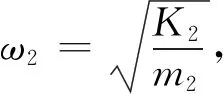
其中：rk为刚度比；rm为质量比；ω1为椅身无阻尼固有圆频率；ω2为人体无阻尼固有圆频率；ξ1为轮胎减振系统的阻尼比；ξ2为坐垫减振系统的阻尼比；η为固有圆频率比.

根据引入的变量，对式(1)进行恒等变换，可得

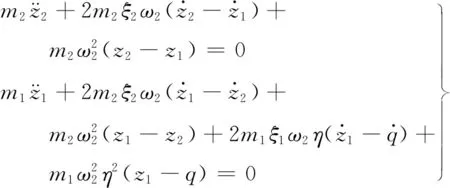
(4)

对式(4)化简，可得

(5)

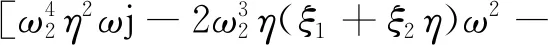
ξ1η+ξ1rm)ω2+ω4]

(6)

式中：j为虚数单位.

2.2 人体振动加速度方均根响应及响应系数

(7)

(8)

式中：h(t)为脉冲响应函数.

人体振动加速度的功率谱密度可表示为

Ga(ω)=E[a(t)a(t+τ)] =

(9)

将式(3)代入式(9)，可得

(10)

人体振动加速度方均根响应可表示为

(11)

将式(10)及代入式(11)，整理可得

(12)

根据留数定理，对式(12)积分，可得

(13)

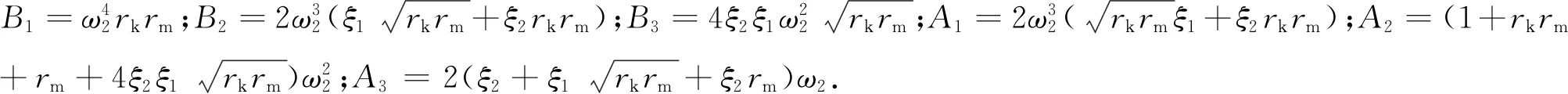
对式(13)进行恒等变形得

(14)

式中：ρ定义为人体振动加速度响应系数，即

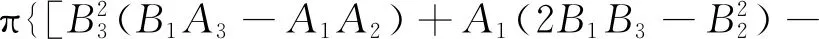
(15)

由式(15)可知：ρ的单位为s-1.5；ρ与rk，rm，ω2，ξ2及ξ1有关，与u及Gq(n0)无关.可见ρ仅由人体-机器人轮椅系统参数决定；ρ值越小，表征机器人轮椅在随机路况下的减振性能越好.

3 人体-机器人轮椅的抑振分析及优化模型

3.1 人体-机器人轮椅阻尼参数的抑制规律分析

轮胎和坐垫作为减振元件，其刚度主要起到支撑和振动缓冲作用，而其阻尼起到振动衰减作用.为了有效抑制并衰减人体-机器人轮椅系统在路面不平顺随机激励下的振动，下文重点分析ξ1和ξ2对人体振动加速度频响函数及ρ的影响规律.

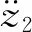
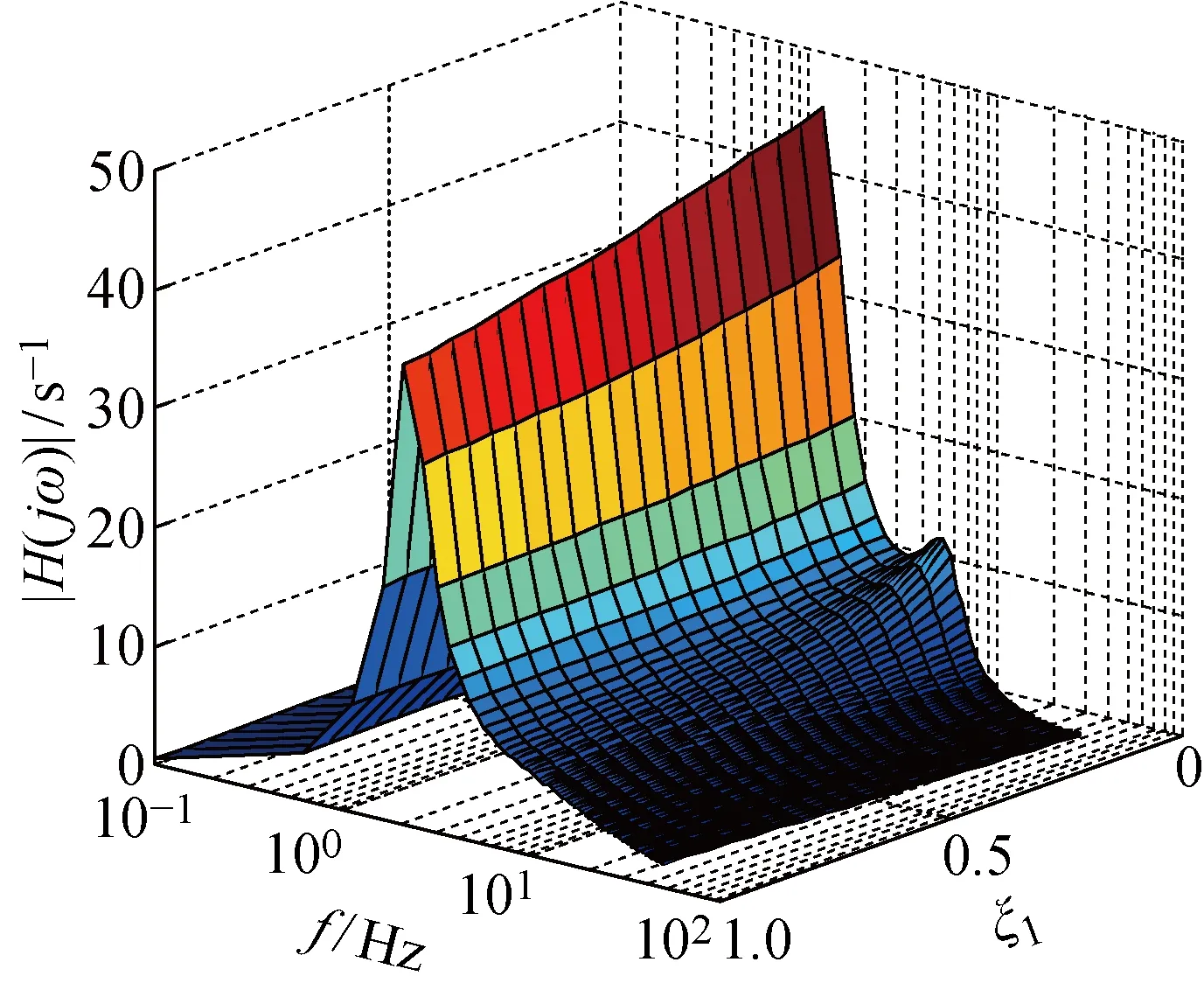
图2 不同ξ1时的|H(jω)|Fig.2 Surface of |H(jω)| with different values of ξ1

图3 不同ξ2时的|H(jω)|Fig.3 Surface of |H(jω)| with different values of ξ2

图4 ρ随ξ1和ξ2的变化曲线Fig.4 Curves of ρ versus ξ1 and ξ2

由图2可知：人体和椅身共振频率分别为2.4和9.0 Hz；当ξ1较大时，可有效抑制人体和椅身共振峰值，但却引起了10.0 Hz后区域幅值的增大.由图3可知：增大ξ2可有效降低人体共振峰，且对椅身共振峰影响很小，但却引起了两共振峰之间非共振区幅值的明显增大.由此可见，ξ1和ξ2过大或者过小均不利于抑制人体-机器人轮椅系统的振动.图4(a)表明，ρ随着ξ1的增大先减小后增大，故ξ1存在最优值使ρ最小化.由图4(b)可知，ξ2也存在最优值使ρ最小化.因此，可通过优化ξ1和ξ2降低人体-机器人轮椅系统的振动.

3.2 人体-机器人轮椅抑振参数的解析优化模型

以ρ最小为优化目标，以ξ1和ξ2为抑振优化变量，建立目标函数J：

min{J(ξ1,ξ2)}=min{ρ}

(16)

坐垫减振系统和轮胎减振系统均为小阻尼隔振系统，故满足如下约束条件：

(17)

对式(16)求ξ2的偏导数并令其等于0，得

(18)

式中：

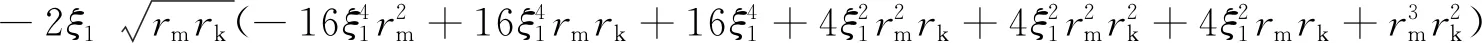
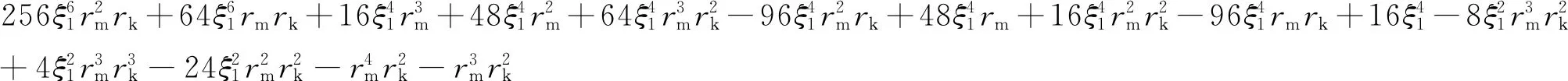
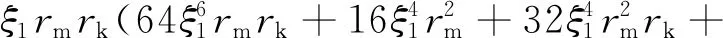
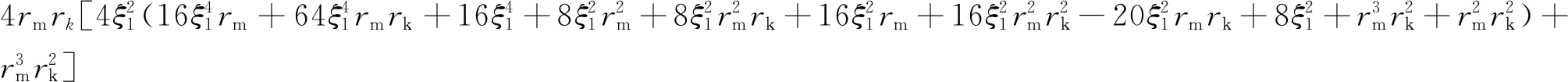
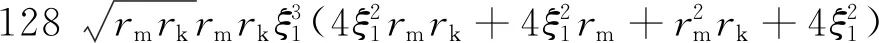
对式(16)求ξ1的偏导数并令其等于0，得

(19)

式中：

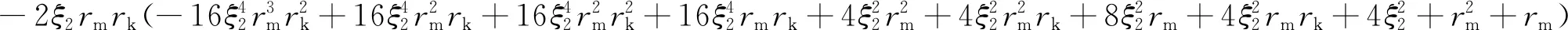
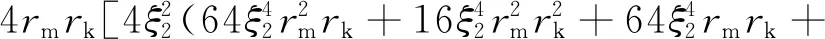
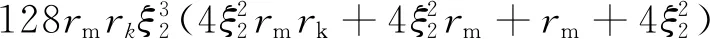
联系式(18)和(19)，可得

(20)

式(20)所有解中满足式(17)的实数解即为使得目标函数J最小化的最优解，简记为(ξ1op,ξ2op).最优解(ξ1op,ξ2op)仅与rk和rm有关，与u及Gq(n0)无关.

在求得(ξ1op,ξ2op)后，根据ξ1和ξ2的定义式，可得轮胎及坐垫的最优阻尼(C1op,C2op)为

(21)

4 优化实例及数值模拟

某型号四轮康复机器人轮椅系统的参数为:K1=80 N/mm，K2=16 N/mm，m1=25 kg，m2=70 kg；机器人轮椅行驶工况为：u=1.0 m/s，水泥人行道Gq(n0)=2.56×10-4m-3.

4.1 解析优化设计

根据上述解析优化模型，可得ξ1op和ξ2op分别为0.55和0.22，C1op和C2op分别为 1 556 N·s/m和466 N·s/m，每个轮胎的阻尼为389 N·s/m.机器人轮椅以u=1.0 m/s行驶在Gq(n0)=2.56×10-4m-3的水泥人行道上时，根据式(13)可得不同ξ1和ξ2情况下的σa，如图5所示.当ξ1=0.554且ξ2=0.219 5 时，σa最小且最小值为0.56 m/s2.此外，根据解析优化结果，可知轮胎及坐垫的最优阻尼比分别在0.5和0.2左右，避免了传统上在0～1之间选取阻尼比的盲目性.

图5 不同ξ1和ξ2时的σaFig.5 Surface of σa with different values of ξ1 and ξ2

4.2 数值模拟

以式(2)生成的时域信号作为输入，利用MATLAB软件自带的ode45算法对式(1)进行求解，进而对机器人轮椅行进在随机水泥路面时的人体振动加速度进行数值模拟.输入信号如图6所示.

图6 水泥路面不平顺随机激励信号Fig.6 Random excitation signal of cement pavement

以σa最小为目标，C1和C2为变量，利用遗传算法进行优化.当σa达到最小值时，可得C1=1 551 N·s/m，C2=469 N·s/m.解析优化模型得出结果与其相对偏差分别为0.3%和0.6%，表明解析优化模型与数值模拟是一致的.解析优化模型与机器人轮椅u及Gq(n0)无关，故无需建立数值模型进行多次模拟优化.与以C1和C2为优化变量相比较，解析优化模型以无量纲阻尼比ξ1和ξ2为优化变量，更具有理论指导价值.因此，该模型便于指导轮胎和坐垫的快速选型及设计.

5 结语

本文建立了人体-机器人轮椅垂向振动模型，提出了机器人轮椅在随机路面激励时的人体振动加速度响应系数ρ；以ξ1和ξ2为优化变量，创建了人体-机器人轮椅抑振参数的解析优化模型.通过理论分析、实例优化及模拟验证，可知：

(1)ρ仅由人体-机器人轮椅系统参数决定；ρ值越小，则机器人轮椅在随机路况下减振性能越好.

(2) 增大ξ1，可同时抑制人体和椅身共振峰值，但会引起椅身共振区后区域幅值增大；增大ξ2可有效降低人体共振峰，对椅身共振峰影响很小，但会引起人体和椅身共振峰之间区域幅值的明显增大.

(3) 解析优化模型得出优化结果与数值模拟结果的相对偏差分别为0.3%和0.6%，证明了解析优化模型的正确性.

(4) 解析优化模型与机器人轮椅行进速度及随机路面谱密度无关，仅和人体与椅身的质量比及轮胎与坐垫的刚度比有关，且以无量纲的阻尼比ξ1和ξ2为优化变量，便于指导康复机器人轮椅设计人员快速进行轮胎和坐垫选型及设计.