离心压气机无叶扩压器非定常流动本征正交分解法

2019-12-31杨晓建胡晨星竺晓程杜朝辉

上海交通大学学报 2019年12期

杨晓建，胡晨星，竺晓程，杜朝辉

(上海交通大学机械与动力工程学院，上海 200240)

离心压气机由于其转速高、单级增压比高、体积小等优点，被广泛地应用于汽车和航空等领域.然而，一旦发生旋转失速等不稳定工况，将会导致离心压气机的压比及工作效率急剧下降，甚至使机器受到严重损害[1].因此，研究离心压气机内部气体的流动状况，特别在小流量工况下，对于理解不稳定流动的产生机理以及如何准确地预判不稳定工况具有非常重要的意义.

扩压器作为离心压气机的主要结构之一，其设计性能的好坏对整个压气机的性能有着重大的影响.根据扩压器内部有无叶片可以分为有叶扩压器和无叶扩压器.无叶扩压器因结构简单、加工更为简便，而被广泛地应用于汽车的涡轮增压器中.Shaaban[2]通过数值模拟对无叶扩压器的几何形状进行优化设计，提高了无叶扩压器内的流动压比，减小了流动损失.Galerkin等[3]采用数值模拟的方法，研究了宽度、进气角度、雷诺数及粗糙度等参数对无叶扩压器性能的影响.Frigne等[4]通过实验的方法测量无叶扩压器内部的非定常流动，对比了不同扩压器内部非定常流动的差异性，并通过Fourier变换分析流场的频率特征.Bianchini 等[5]通过实验测量无叶扩压器内部的流动，建立了一种预测离心压气机喘振和旋转失速的方法.Jaatinen-Värri等[6]通过实验测量及数值模拟，研究了不同宽度对无叶扩压器压气机整体性能的影响.研究结果表明：宽度过窄会导致气流在无叶扩压器中的加速过快，从而较容易产生非均匀流及近轮盖一侧的流动分离.

非定常数值模拟方法作为一种有效的、可靠的方法被广泛地应用于叶轮机械领域.Tamaki[7]利用数值模拟方法，计算不同工况下离心压气机的总体性能，并进行了实验验证.研究结果不但验证了计算流体力学(CFD)在流场分析中的准确性与可靠性，还预测了小流量工况下的压比及工作效率等参数.Turunen-Saaresti 等[8]利用数值模拟方法，获得了无叶扩压器内部三维流场的压力分布，并进一步分析了流动的非定常特性.Abdelwahab[9]基于非定常数值模拟方法研究无叶扩压器内部的流动特性，揭示了二次流及尾迹流在无叶扩压器段的相互作用，并进一步基于涡方法提出了用于描述无叶扩压器内部尾迹流的发展模型.Zheng 等[10]通过非定常数值模拟方法对带有无叶扩压器的高速离心压气机进行研究，揭示了无叶扩压器内部流动不稳定的产生机理：不稳定流动主要是由主流及叶顶区域回流之间的相互作用而形成的“回流涡”和叶顶间隙泄漏流两者共同产生的；而后受到下游蜗壳的非对称作用影响，最终形成喘振.郭强[11]通过数值模拟方法计算离心压气机在不同工况下的流场，发现在无叶扩压器近轮盖一侧的进口区域及出口区域产生了回流区，并进一步分析了径向逆流形成的原因.Zhu 等[12]通过非定常数值模拟方法，获得了某离心压气机的总压损失系数以及静压恢复系数随质量流量的变化关系，并进一步分析了无叶扩压器失速的形成机制.

无叶扩压器中的流动具有高度非定常特征，采用非定常数值模拟方法可以获得不同时刻下流场的流动结果.为了深入研究非定常流场的流动信息及流动结构，需要对上述结果进行降维处理.一种流场降维方法是动态模态分解(DMD)法，DMD法通过分解流场可以获得不同特征频率所对应的模态[13].另一种流场降维方法是POD法，POD法能够将流场分解成一组相互正交的模态，并以能量的大小衡量不同模态在整个流动中所占的比重[14].利用POD法分析失稳工况下的无叶扩压器内部流场快照，并通过分解获得流场中大尺度的流动结构.值得注意的是，通过POD法获得的无叶扩压器的失速模态，有助于加深对离心压气机无叶扩压器内部失速流动的形成及其发展过程的理解.POD法在流场分析中有着广泛的应用.Sirovich[14]提出“快照POD法”，该方法由于可以提高计算效率而被广泛地用于流场分析.Cizmas等[15]利用非定常数值模拟方法计算涡轮内部的流场，并用POD法分析计算结果，获得该级涡轮主要的流动特征，并基于此进行流场重构.研究结果表明：采用前40阶模态进行重构获得的流场能量变化误差小于0.6%，验证了该方法的可靠性.Wei 等[16]通过粒子图像测速(PIV)法测量低雷诺数下的翼型流场，并利用POD法分析测得的数据发现，由翼型的前缘与尾缘产生的分离剪切层占据了最高能量体积质量，而对应于尾缘脱落涡的高阶模态占据的能量体积质量较小.Yang 等[17]通过POD法分析了圆盘尾迹流，获得了不同雷诺数下的模态及流场结构特征，并揭示了其对于流动稳定性的影响.

本文采用POD法研究离心压气机无叶扩压器内部的非定常流场.首先，采用非定常数值模拟方法求解带有无叶扩压器的离心压气机的流场，获得小流量工况下的流场数据；然后，通过POD法分析无叶扩压器内的流动特性，获得该流场的主要模态；同时，将不稳定的模态进行流场重构，揭示失稳流动的发展过程；最后，研究不同采样频率对POD法分析结果的影响.

1 离心压气机的整机数值模拟

1.1 研究对象

研究对象为某单级高速离心压气机，其中包括离心叶轮、无叶扩压器和蜗壳，并在出口处添加出口管道以调节质量流量；叶轮的叶片数为12个，其中包括6个主叶片和6个分流叶片.叶轮设计工况下的工作转速为 44 198 r/min；设计工况下的质量流量率m为1.8 kg/s.离心压气机的结构及几何参数如表1所示.其中，蜗壳A/R为蜗壳的面积半径比.

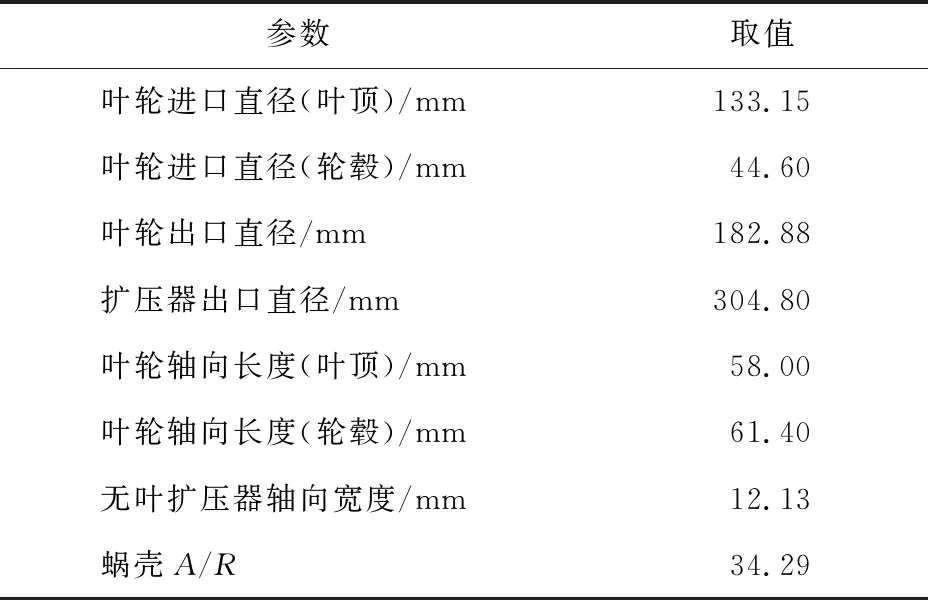
表1 离心压气机几何参数Tab.1 Geometry parameters of the centrifugal compressor

图1 离心压气机的各部件网格图Fig.1 Mesh of the components of centrifugal compressor

1.2 网格模型与数值计算设定

采用商业软件ANSYS ICEM和TurboGrid对离心压气机进行网格划分.离心叶轮和无叶扩压器采用TurboGrid软件进行结构化网格划分；蜗壳和出气管采用ICEM软件进行网格划分.其中，蜗壳部分划分非结构化网格，出气管部分划分结构化网格.离心压气机的各部分网格示意图如图1所示；采用3套网格(M1、M2、M3)进行网格无关性检验，如图2所示，其中π为总压压比.综合考虑网格数量与计算量的影响，最终选择总网格数为2.904×106个，叶轮部分网格为1.03×106个的方案.

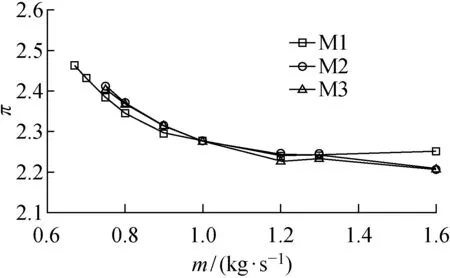
图2 网格无关性检验结果Fig.2 Results of mesh number independence verification

数值计算包括定常计算和非定常计算两部分.定常数值计算的边界条件设置：进口给定总温为300 K；总压为101.325 kPa；轴向进气；出口给定静压；湍流模型选择SSTk-ω模型；稳定计算的收敛条件为最大残差小于10-3.将定常计算的结果作为非定常计算的初场，非定常计算的边界条件设置与上述相同，时间步长设定为1.131×10-5s，即2个大叶片中间流道对应的步数为20步.数值计算采用动网格技术，通过改变排气管出口(见图1(c))的大小达到调节质量流量的效果，以模拟实际中不同质量流量下离心压气机的工作工况[12].

1.3 数值模拟结果验证

根据上述数值模拟结果，可以获得不同质量流量下的离心压气机的性能参数，并与实验结果进行对比，如图3所示.

图3 数值模拟结果与实验结果对比图Fig.3 Comparison between numerical simulation and experimental results

由图3可知，两种方法的数值结果吻合得较好，初步验证了该数值模拟方法的可靠性.在设计工况下，离心压气机的m=1.8 kg/s.随着m逐渐减小，总压比先略微升高，大约在m=1.5 kg/s处总压比达到最高点，然后再逐渐下降；当m=1.4 kg/s时，压气机无叶扩压器内部的监控点检测到了压力及质量流量的波动.非定常计算中设置的监控点位置如图4所示，其中，P1位于无叶扩压器内部，P2位于排气管内部.

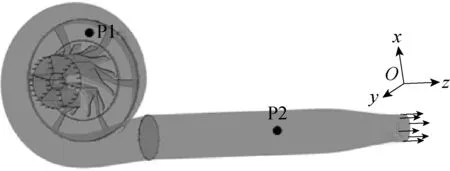
图4 监控点位置Fig.4 Positions of monitor points

当m=1.4 kg/s时，无叶扩压器内部监控点P1的频谱分析结果如图5所示.其中，A为振幅；f为频率.由图5可知，频谱分析捕获到了对应于全叶片扫描频率的 8 840 Hz，对应于主叶片扫描频率的 4 420 Hz，以及低于转子旋转频率的230 Hz(该频率为离心压气机的失速频率)，即在该工况下离心压气机出现了失稳现象[18].因此，下文将主要分析m=1.4 kg/s时的工况.

图5 无叶扩压器内部监控点的频谱分析结果Fig.5 Spectrum analysis of the monitor point inside the vaneless diffuser

当m=1.4 kg/s时，不同时刻下无叶扩压器靠近轮毂10%处的径向平面上的径向速度v以及压力p的分布云图如图6所示.其中，叶轮旋转方向及蜗舌位置在图中均已标出；T为扰动周期，单位为s，数值上取频率230 Hz的倒数.由图6可知，不同时刻下流场的主要流动结构并没有发生明显的改变，但存在幅值较小的波动.下文将通过POD法分析流场，进一步研究其非定常特征.

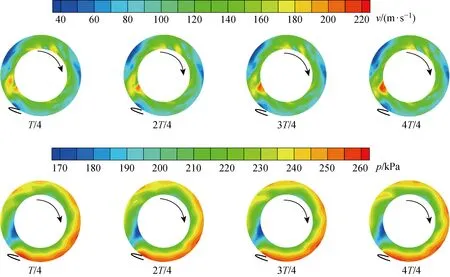
图6 不同时刻下无叶扩压器内部v和p的分布云图Fig.6 The distribution of v and p inside the vaneless diffuser at different times

2 POD法

无叶扩压器中的流动是复杂的三维非定常流动，为了进一步探究该非线性系统中的特征、识别流场中大尺度的流动结构，通过POD法对其进行分析.在流场分析中，应用比较广泛的是“快照POD法”[14].

不论是基于实验测量或是非定常数值模拟，假定有一组随时间变化的参数，即一系列的快照，提取每张快照中的参数波动量，将这些波动量构成一个矩阵，则有

U=[u1u2…uN]

(1)

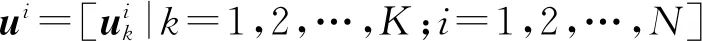
因此，该矩阵的自协方差矩阵可以表示为

C=UTU

(2)

对其求特征值和特征向量，则有

CW=λW

(3)

式中：λ为特征值矩阵；W为特征向量矩阵.将获得的特征向量矩阵按对应的特征值从大到小排列，其中特征值的大小表征其所对应模态在整个流场中所占相对体积质量的大小.

将按照特征值从大到小的顺序排列好的特征向量用于求解各阶POD模态，即

(4)

式中：分母为2范数.则原有的流场可以通过POD法中各阶模态的线性组合来表示，其中各阶POD模态所对应的系数被称为POD系数，可通过下式获得，即

an=ΨTun

(5)

式中：Ψ为各阶模态的组合，即

Ψ=[φ1φ2…φn]，n=1,2,…,N

将式(5)进行变形，获得每个流场快照采用POD模态表示的形式，即重构方程为

(6)

3 无叶扩压器流场的POD分析

3.1 非设计工况下POD分析

针对m=1.4 kg/s工况，应用商业软件ANSYS CFX进行非定常数值模拟，总计算步数为800步.每2步时间间隔就输出1次计算结果，最大采样频率为44.209 kHz.模拟结果共获得400个时刻的流场计算结果，即400个流场快照，并基于此进行POD分析.

通过POD法分析上述400个流场快照.不同时刻下，平均流场的v和p的分布云图如图7所示.由图6和图7可知，不同时刻流场的主要结构基本上由平均流场构成.基于POD法计算获得的各模态特征值从大到小排列的分布如图8所示.由图8可知，前40阶POD模态占全部波动能量的99.0%，前6阶POD模态占总波动能量的89.5%.因此，主要关注前6阶的流动模态.

图7 平均流场v和p的分布云图Fig.7 The distribution of v and p of the mean flow

图8 由POD分析获得的特征值分布Fig.8 Distribution of eigenvalues obtained by POD analysis

非设计工况下，POD分析获得的前6阶模态所对应的归一化后的压力及径向速度云图如图9和10所示.由图9可知，第1，2阶模态在整个无叶扩压器的周向存在高压与低压交替出现的压力波动，且波动数目恰好是12个，说明该压力扰动与总叶片数一致.虽然第1，2阶模态在特征值上略微存在差异，但由于其压力波动分布近乎相似，故可以认为第1，2阶模态为一对配对模态.二者在相位角上的差异将形成周向传播的波，类似于上游动叶出口处射流-尾迹结构的扫描运动.第3，4阶模态的压力云图存在周向6个高低压力团的交替排列，虽然两者的特征值差异比第1，2阶模态的特征值大，但也可以认为是一对配对模态，能够形成周向波动的传播特征.分析径向速度模态可以得到类似的结论，故在此不再赘述.

各阶POD模态在上述的400个流场快照所对应的采样时间内的POD系数随时间的变化曲线如图11所示.由图11可知，在采样时间段内的曲线呈现周期性的变化特征.对该系数进行Fourier变换可知，1阶和2阶模态的特征频率基本相同，以 8 841.7 Hz为主，4 420.9 Hz次之，说明这两阶模态是由于叶片的旋转造成的；3阶和4阶模态的主要特征频率以 4 420.9 Hz为主，8 841.7 Hz次之，同样也对应主叶片的扫描频率；5阶和6阶模态的特征频率为221.04 Hz，对应离心压气机的失速频率，说明这两阶模态构成了失稳流动的波动特征，但6阶模态在能量上远小于5阶模态.

图10 前6阶POD模态所对应的径向速度云图Fig.10 The radial velocity distribution of the first six POD modes

图11 POD模态的系数随时间的变换曲线Fig.11 The coefficient of POD modes changing with time

图12 径向速度模态的重构结果Fig.12 Reconstruction results of radial velocity modes

3.2 对失速模态进行重构

为了进一步理解失稳流动的发展过程，选取5阶和6阶模态进行流场重构.5阶和6阶模态的失速频率所对应周期内不同时刻的径向速度分布如图12所示.由图12可知，无叶扩压器的周向有多个扰动分布，蜗舌下游90° 位置的扰动幅值最大，并且扰动没有沿周向进行传播，而是以径向波动为主.

3.3 不同采样频率对结果的影响

将采样频率变为每5步提取一个快照，即尾迹和射流区在周向交替出现.前20阶特征值的分布和前6阶POD模态的压力云图如图13和14所示.

对比图10和14，可以发现图10中的第3，4，5，6阶模态与图14中的第2，3，4，5阶模态基本接近，即图10中的第1，2阶配对模态在图14中只存在1阶，改变了原来周向传播的特征.这可能与采样频率直接相关，每5步提取一个快照，即大小叶片的尾迹和射流区在周向交替出现，而叶片的射流-尾迹结构在空间类似驻波形式.为此在采样时需要注意，尽量避免采样频率和流动特征频率一致或相差整数倍.