深孔啄钻振动信号DTW算法改进及应用*

周友行， 李 勇， 刘镇海， 赵晗妘， 刘汉江

(1.湘潭大学机械工程学院 湘潭，411105) (2.复杂轨迹加工工艺及装备教育部工程研究中心 湘潭，411105)

引 言

在航空航天、汽车、电子等领域，深孔类零部件的应用日趋广泛，其钻削加工质量直接影响产品的工作性能[1]。传统钻削加工工艺系统刚度差、排屑和切削散热困难，同时钻削过程处于封闭或半封闭环境，很难实现高效、高精度、低成本的加工质量检测需求[2]。随着计算机和传感器技术的发展，可实现以传感器信号为对象的钻削过程中钻杆力学行为分析[3]、工艺参数优化[4]、刀具结构改进[5]、刀具状态识别[6]和切削过程监测[7]。近年来涌现了大量基于监测信号的钻削质量研究：Rimpault等[8]采用切削力分形分析对钻头磨损和表面质量进行监测；Qin等[9]研究机器人钻削过程中的振动信号来分析加工表面质量；Ferrari等[10]利用声发射信号评估钻孔质量；Costes等[11]通过对振动、声发射和切削力多传感器信息融合探究加工表面质量与其之间的关系。这些研究表明，钻削过程监测信号波动能反映钻削质量变化。

啄钻过程中，由于其采用间歇性进给加工，监测信号会呈现明显的间断性。在相同加工条件下，理论上每次啄钻进给量相同，则对应啄钻进刀阶段监测信号波形一致。如果某一啄钻阶段出现加工异常导致钻削质量变化，同样会体现在啄钻监测信号波动上。因此，分析比较各啄钻阶段信号的一致性，可以判别深孔加工质量的一致性。要实现基于监测信号的深孔加工质量异常判别，关键在于如何准确分割出与每一个啄钻阶段匹配的监测信号和如何分析各啄钻阶段监测信号的一致性。基于此，笔者以啄钻振动信号为例，提出双窗双谱检测算法分割信号，采用改进DTW算法评估啄钻阶段振动信号的一致性，从而实现深孔加工质量异常的识别。

1 深孔啄钻质量异常检测思路与流程

1.1 深孔啄钻过程及振动信号

如图1所示，深孔啄钻过程采用不断的进刀、退刀动作进行间歇进给加工，每次保持恒定进给量加工后均从孔内退出，然后再钻入孔中直至加工过程结束。

如图2所示，深孔啄钻的间歇进给使监测信号呈明显的间断性。因此，深孔啄钻过程振动监测信号可描述如下

A(n)=[a1,A1,a2,A2,…,ai,Ai,ai+1]

(1)

其中：n为振动信号长度；Ai为第i次啄钻进刀振动信号；ai为刀具空切削信号。

图1 深孔啄钻加工示意图

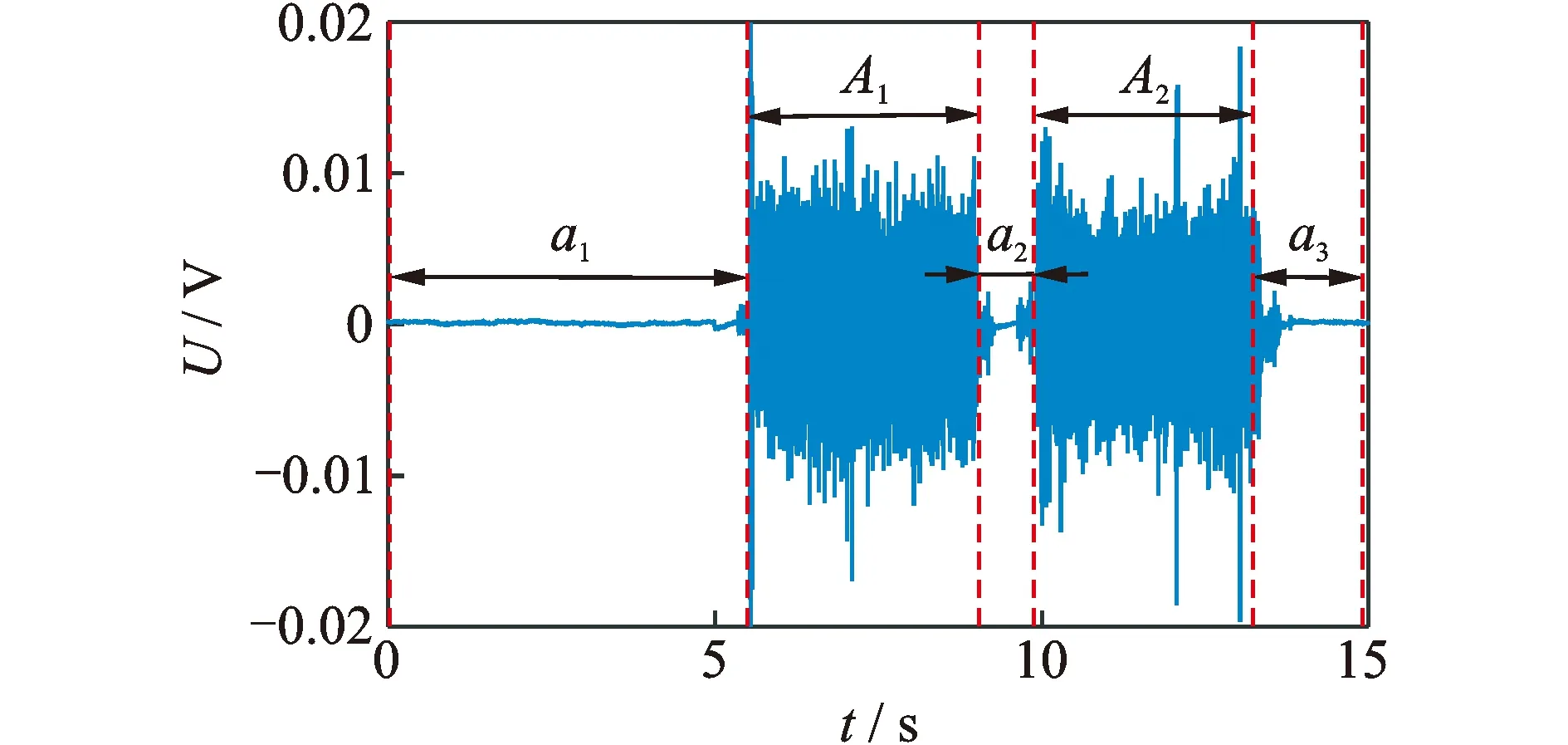
图2 深孔啄钻振动信号

1.2 深孔啄钻质量异常检测流程

若啄钻过程正常，深孔I，II段加工质量基本一致，理论上A1和A2信号波形应一致，否则信号A1和A2会出现波动变化。因此，通过研究信号A1和A2相似性程度可以判别深孔加工质量的一致性。

要实现基于监测信号的啄钻加工质量一致性评估，前提是从整个监测信号中准确分割出A1和A2信号，但深孔啄钻环境复杂，监测信号采集受外界因素影响较多，容易产生较强噪声。笔者针对传统基于能量的双滑动窗口信号检测算法对噪声敏感的问题，引入对噪声具有抑制作用的双谱统计量，力求实现更加准确的信号分割。同时，提出改进DTW算法实现非严格等长分割信号的一致性评估。

笔者提出图3所示的基于振动信号的深孔啄钻加工质量异常检测流程。首先，基于深孔啄钻加工振动信号，利用双窗双谱算法分割信号并进行特征降维；其次，采用改进DTW对非等长特征进行规整处理；最后，以累积最短规整路径距离评估分割信号的一致性，从而实现啄钻质量异常的检测分析，并结合实际钻削试验物理检测结果对方法进行验证。

图3 基于振动信号的深孔啄钻加工质量异常检测流程

2 理论方法

2.1 双滑窗双谱信号检测算法

将深孔啄钻振动信号A(n)视作随机序列，其3阶相关函数为

C3(m1,m2)=E[A(n)A(n+m1)A(n+m2)]

(2)

其中：E为期望运算；m1，m2为信号点数的排序，且满足m1≤m2。

双谱是3阶累积量的二维傅里叶变换[12]，即A(n)的双谱为

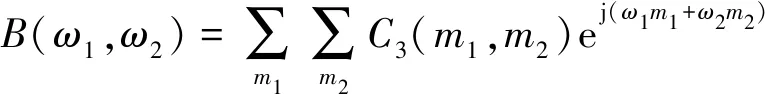
(3)

其中：ω1，ω2为频率分量。

判决量mn的定义如下

(4)

在刀具开始切削工件前，两滑动窗内基本只含有噪声信号，因此双窗内双谱的比值判决量mn几乎没有变化；当刀具开始切削和结束切削时刻，随着窗口滑动，双窗内的双谱比值判决量会发生突变。为此，通过设置合理阈值Th，根据mn的变化情况就能判断出啄钻进刀阶段信号的起止和结束时刻。

2.2 动态时间规整算法的改进

1) 动态时间规整算法。

动态时间规整(DTW)是评估两长度不等时间序列相似度方法[13]。假设长度为a和b的两啄钻进刀信号S和T(S，T∈Ai)表示为

(5)

构造一个a×b的矩阵R，矩阵中的每个元素rij=d(si,tj)=(si-tj)2代表序列si,tj两点的距离。算法的核心是寻求最优规整路径W={w1,w2,…,wk,…,wK}，其中wk=(rij)k满足和对齐时相应的累积距离最短。对于规整路径的选取需满足以下约束条件

(6)

其中:0≤i-i′≤1；0≤j-j′≤1。

最小规整代价路径可表示为

(7)

累积最短路径D(m,n)可评估啄钻进刀信号S和T的一致性，其计算公式如下

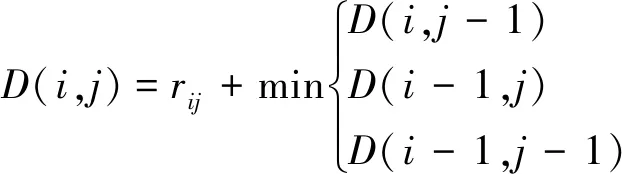
(8)

2) 动态时间规整算法的改进。

DTW一直存在时间复杂度高和病态规整问题[14]。病态规整是指一个序列的很多点映射到另一个序列的一个或几个点上的极端情况(奇点现象)，奇点现象会严重影响序列一致性评估。

对于时间复杂度高的问题，其原因在于动态规划寻找最优规整路径时，算法遍历了整个距离矩阵节点来求累积距离，极大地占用了计算时间。实际上在式(6)的约束下，规整路径主要分布在累积距离矩阵对角线上，故可以施加窗口约束来限制规整路径处于矩阵对角线范围内，从而减小计算量。

为此，笔者引入斜率权重参数α，β来控制规整路径偏向对角线程度，则累积最短路径D(m,n)由式(9)计算

(9)

对于奇点问题，Keogh等[15]提出的导数动态时间规整算法(derivative dynamic time warping，简称DDTW)极大地改善了这种现象，DDTW在传统DTW只将序列的幅值作为一致性评估外，加入了序列形状等局部特征，即采用序列导数来代替原始序列

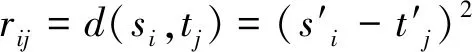
(10)

DDTW中导数引入取得的可观结果，值得对类似方法的进一步研究。数学变换在时间序列分类中有着广泛应用，但其应用主要还是局限于对计算效率的提升和数据高阶特征的提取[16]。

笔者尝试引入变换计算距离的概念，将变换作为时间序列距离度量的组成部分。如果选择的变换是等距变换，则该变换的引入不会增加任何对时间序列距离度量有效的新信息，因为其仅仅是度量空间的保距映射，故引入非等距变换来提高度量的准确性是合理的。

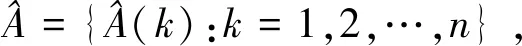
(11)

(12)

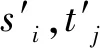
那么改进动态时间规整算法的累积最短路径D(m,n)计算如下

(13)

3 仿真及钻削试验分析

3.1 仿真分析

1) 信号分割仿真分析。

仿真信号定义为

x=0.01t_index.sin(2π20t)

(14)

信号产生时间段为0.3～0.5，0.8～1.1和1.5～1.9s，对信号加噪后采用双窗双谱算法进行检测分割，分割如图4所示。

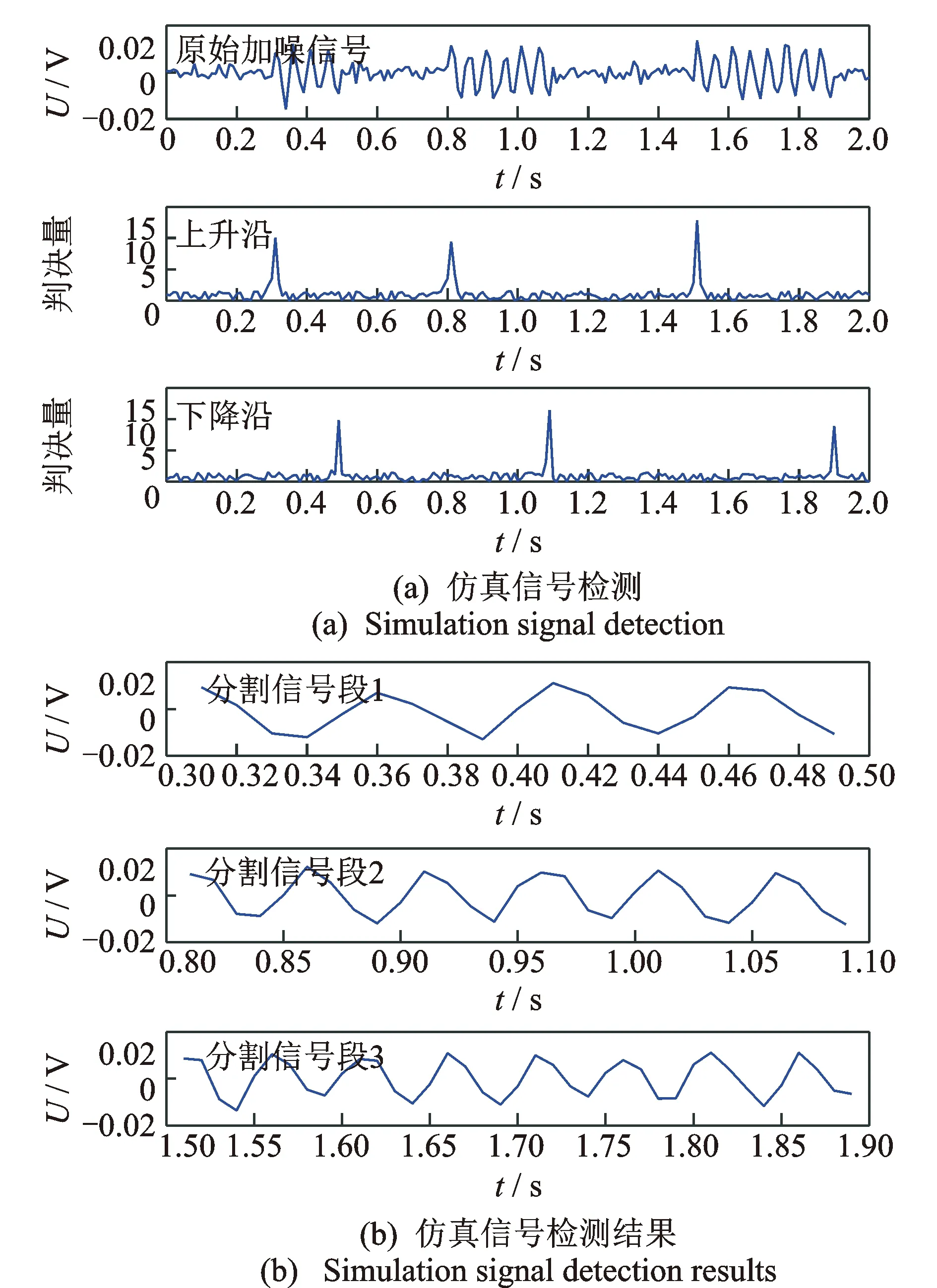
图4 双窗双谱信号分割仿真分析

2) 改进的动态时间规整仿真分析。

从图4发现分割后信号长度不一，传统的距离度量(如欧氏距离)不适用于上述分割信号的一致性评估，因此引入DTW算法。分别利用传统DTW和改进DTW对上述分割信号段1和2进行规整对齐，其规整结果如图5所示。

从图5(a)中可以看出，传统DTW会出现病态规整现象，因为算法要求两序列的点严格一一对齐，造成了如图中用圈所标记的S2中很多点与S1中某一个点相映射形成的“奇点”；而改进的算法更具柔性，不要求所有的点严格对齐，而是从序列趋势上去进行规整对齐。

图5 动态时间规整和改进后算法的规整对齐示意图

由图5(b)可以看出，算法效率的提升体现在规整路径选取上，DTW和改进的DTW求得的DTW距离分别为0.217和0.044。DTW距离代表了两序列的相似性，其值越大，说明序列间差异越大；其值越小，说明序列间越相似。实际上从仿真信号定义可以得出两段序列是同一函数，不同之处在于长度不同，计算的DTW距离值越小越能证明算法改进的有效性。

3.2 钻削试验

笔者以深孔钻削过程振动监测信号为研究对象，相关深孔啄钻加工试验如图6所示。试验中加工孔径d=5 mm，孔长l=30 mm。

图6 深孔啄钻加工试验

加工设备如下：机床为VMC-C30；加工刀具为直径为φ5的Kennametal钻头；传感器为Kistler8793A三向加速度振动测试仪，并将其安装于机床主轴和工件上，主要是对机床主轴振动进行分析，而工件振动作为参考；加工材料选用尺寸规格为150 mm×130 mm×30 mm的TiAl6V4钛合金板材，信号采集设备采用美国国家仪器公司(NI)的NI PXle-1082机箱，采样频率为20 kHz。试验加工参数如表1所示。

表1 加工工艺参数

Tab.1 Drilling processing parameters

钻削深度/mm每次啄钻深度/mm主轴转速/(r·min-1)进给量/(mm·min-1)305800150

3.3 钻削振动信号分割与加工质量分析

将试验采集的钻削振动信号进行去噪滤波等预处理后，分别利用双滑动窗口算法和双窗双谱算法进行信号检测分割，分割的效果如图7所示。可以看出，传统的双滑动窗口信号检测算法对啄钻振动信号进行分割时，受到噪声干扰分割结果不尽人意，而双窗双谱算法能准确有效地进行分割。

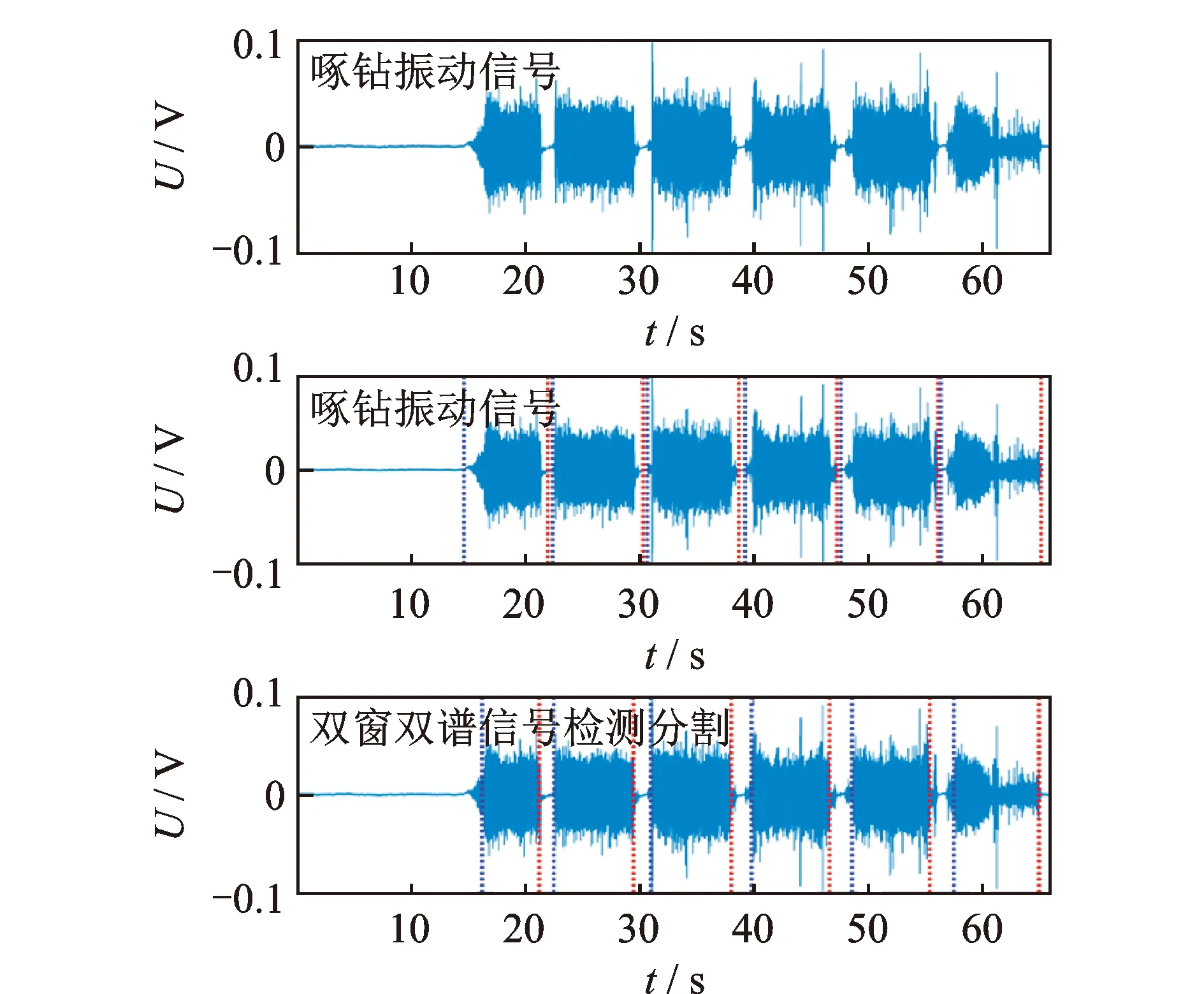
图7 深孔啄钻振动信号分割

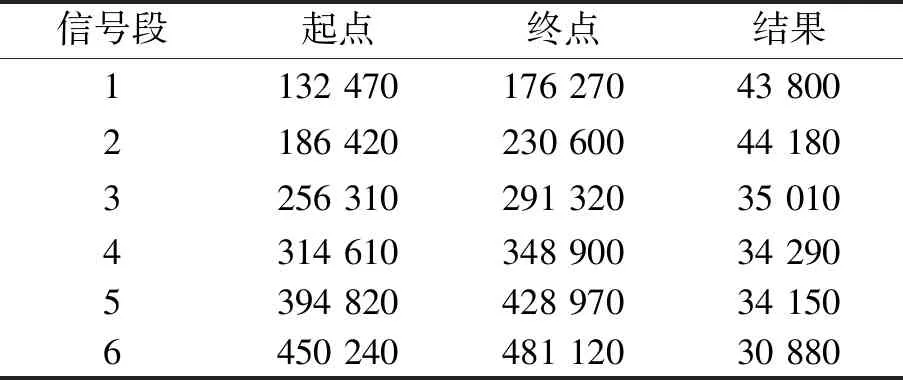
表2 振动信号分割结果

从表2可以得出，由于算法误差和环境噪声等影响，理论上每段长度相等的啄钻进刀振动信号并不等长，因此对它们的一致性评估引入了DTW算法。为减少计算量，对信号进行特征降维，同时提取信号时域和频域特征后形成新的组合特征。时域内，选取窗长为Wl的滑动窗口在长度为L的振动信号上以窗移长度为Ws移动时，每个窗口内的曲率和斜率作为特征，其表示为

(15)

频域内，选择2阶Daubechies(db2)小波23尺度上的细节系数作为特征[17]，其表示为Ff=[x1,x2,…]，则分割信号Ai的组合特征定义为

(16)

因此，对啄钻进刀振动信号的一致性评估可以转换成组合特征之间的一致性评估。提取6段信号的组合特征F(1),F(2),…,F(6)，并利用改进的DTW进行相似性度量，以时间为序求解连续两啄钻进刀信号特征的DTW距离(无量纲)，结果见表3。

表3 啄钻振动信号段DTW距离

Tab.3 The DTW distance of peck drilling vibration signal segment

信号段1和22和33和44和55和6DTW距离0.745 10.824 60.904 50.964 02.531 7

图8是以信号段5和6的组合特征为例，进行改进DTW对齐和最终累积最短规整路径距离的结果。

图8 深孔啄钻振动信号特征规整结果

在求出组合特征之间的DTW距离后，将其与设定的阈值Th′=2相比较，如果该距离大于该阈值，则认为这两段信号存在较大的差异，同时判定对应啄钻加工质量差异较大，即加工质量出现异常；若距离小于该阈值，则认为这两段信号基本相似，某种程度上可以认为其加工质量近似。从计算结果DTW56=2.531 7>Th′可以判定在编号6处的孔段出现质量异常。

在钻削加工试验结束后，采用线切割切开钛合金试验板，选取某孔利用JB-4C精密粗糙度测试仪进行表面粗糙检测，同时利用高倍显微镜观察孔内表面质量，如图9所示。经过粗糙度检测和表面质量观察发现，该孔编号为6孔段的粗糙度为1.554，明显高于孔内其他部分，即加工质量出现异常。

图9 深孔啄钻加工物理检测示意图

4 结 论

1) 当啄钻切削参数一致、加工正常时，啄钻进刀阶段振动信号理论上波形一致；加工异常时啄钻阶段振动信号之间呈较大差异，这种差异变化同样体现在啄钻质量波动上。

2) 双窗双谱算法改善了传统基于能量的双滑动窗口检测算法对噪声敏感的问题，对噪声环境下各啄钻进刀阶段振动信号能进行有效分割。

3) 动态时间规整算法的改进，主要涉及规整路径斜率约束和在导数动态时间规整基础上引入余弦变换，使算法更加柔性来减少病态规整。对于传统DTW只将序列的幅值作为一致性评估的不足，改进算法不仅充分结合了序列形状等局部特征，同时余弦变换丰富了原始序列的表征信息，其在提升算法效率和避免奇点现象上具有明显效果。

4) 基于深孔啄钻振动信号，利用双窗双谱算法分割信号并进行特征降维；针对分割信号特征不等长特点，利用改进的动态时间规整进行处理；最后以累积最短规整路径距离作为衡量啄钻进刀阶段振动信号的一致性评估，从而实现振动信号对应孔段钻削质量异常的识别分析。仿真分析和试验计算结果表明，以振动监测信号各啄钻阶段信号的一致性评估来实现深孔质量异常识别是可行的，其研究结果也可为深孔质量检测提供一种新思路。