非线性-线性联合减震控制方法频谱特性分析*

2019-12-31王菁菁刘志彬李浩博岳洪滔

振动、测试与诊断 2019年6期

王菁菁，刘志彬，李浩博，岳洪滔

(1.广州大学土木工程学院广州，510006) (2.湖南工业大学土木工程学院株洲，412000)

引言

结构控制技术通过对控制装置所依附的结构施加被动或主动的作用力，改变结构主体的刚度、质量和阻尼等，以达到减小能量输入和加速能量消耗的目的[1-2]。目前，基础隔震、TMD以及各类阻尼装置[3]等结构控制技术已经被大量运用到实际工程之中。TMD是应用最为广泛的被动控制技术之一，远小于主体结构质量的TMD在运动过程中消耗大量能量[4-8]。为了使结构响应有效减低，TMD的自振频率被调至与主体结构相近，但也因为如此，TMD只在较窄的频率范围内运作良好。在连续地震作用下控制结构TMD的鲁棒性难以保持，减震效果相对减弱[9]。NES是一种新型的被动控制方法。非线性能量阱由一个质量或一组质量组成，通过阻尼单元和非线性的弹簧单元与主体结构相连，使其产生本质非线性的回复力，因此NES能够在较宽频带发挥控制作用[10-12]。其中一型NES研究较多，在一型NES的现象学模型中，NES质量块通过立方刚度的弹簧单元和黏滞阻尼单元与主体结构相连。通过对某2层结构模型分别附加一型NES和TMD在地震作用下的响应对比可知，当主体结构固有频率发生变化时，NES仍表现卓越[13]，但同时一型NES减震性能容易受到初始能量的影响，在初始能量不同时减震效果差别较大。

为解决上述问题，笔者提出了将非线性和线性两类控制方法联合使用的结构控制方法，使一个或一组装置同时具备TMD的线性特点和NES的非线性特点，在脉冲型荷载作用下，非线性-线性联合的控制方法展现出较强的能量鲁棒性和频率鲁棒性[14]。刘良坤等[15]对TMD与NES并联的控制方法利用复变量平均法和多尺度法进行了分析，结果表明混合系统既拓宽了频带又降低了对初始能量的敏感性。

笔者在某8自由度主体结构模型上附加TMD、一型NES、单质量联合阻尼器和双质量联合阻尼器4种控制装置。首先在脉冲型荷载作用下进行参数优化，考察了各控制方法的能量鲁棒性和频率鲁棒性。然后在7条实测地震作用下进行减震效果对比和分析，并根据地震反应谱和系统频谱特性讨论各类控制方法的减震性能差异。

1 非线性-线性联合阻尼器

1.1 单质量联合阻尼器

单质量联合阻尼器(简称单联)在附加质量运动正负方向分别采用非线性和线性回复力-位移关系，如图1所示，是一种构造紧凑、占用空间相对较小的结构控制方法。单联在正方向上遵循3次方回复力-位移关系，与一型NES相同；在负方向上遵循线性回复力-位移关系，与TMD相同，如图2所示。

图1 单质量(左)与双质量(右)联合阻尼器示意模型

图2 单联回复力-位移关系

单联运动方程为

其中：ma为附加质量；Ca为附加质量的黏滞阻尼系数；kasN和kast分别为附加质量非线性和线性刚度系数；ua为附加质量相对于主体结构位移；xhost·abs为主体结构绝对位移。

1.2 双质量联合阻尼器

双质量联合阻尼器(简称双联)使用2个附加质量(见图1)，包括1个非线性质量(即一型NES)和1个线性质量(即TMD)。两者不直接接触，同时与主体结构发生相互作用。

2个附加质量的运动方程分别为

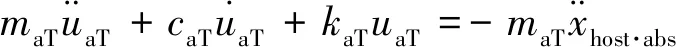
(2)

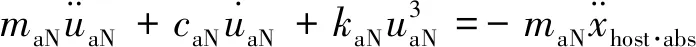
(3)

其中：maT和maN分别为双联中TMD和NES的质量；caT和caN分别为TMD和NES的黏滞阻尼系数；kaN和kaT分别为TMD和NES的刚度系数；uaT和uaN分别为TMD和NES相对于主体结构的位移。

2 控制参数

2.1 优化条件

为考察所提出两类联合阻尼器的减振性能，笔者将单联、双联以及用于对比的一型NES和TMD分别置于同一主体结构顶层，并采用相同优化方法对各质量阻尼器控制参数进行优化。优化在Matlab中通过建立Simulink模型进行。所采用主体结构为8层钢框架结构[16]，首层高为3.9 m，其他层高为3.3 m。简化为1个8自由度层串模型，使用State-space模块模拟。各层质量为2.3×105kg，刚度为3.9×108N/m，模态阻尼比为0.02，前3阶自振周期分别为0.83，0.29和0.17s。优化采用脉冲型荷载，通过设置初始运动条件施加，使各质量(包括主体结构和控制装置)具有0.25 m/s的初始速度。优化目标为使各控制系统中主体结构顶层位移10 s内均方根达到最小值。当控制装置附加质量越大时，其减振效果越显著，但考虑到实际结构中空间和装置体量的限制，控制装置质量均取为主体结构质量的3%，即5.52×104kg。各控制装置采用相同大小黏滞阻尼，参考TMD最优阻尼计算方法[17]，为9×104(N·s)/m。

2.2 优化结果

单联待优化参数为线性和非线性刚度系数，通过依次计算不同线性与非线性刚度系数组合下的结构响应(顶层位移均方根)进行选择。优化结果如图3所示，最优线性和非线性刚度系数分别为1.34×106N/m和1×109N/m3(图中圆点所示)。

图3 单联刚度优化结果

双联中总附加质量为5.52×104kg，线性和非线性质量各占50%，两质量阻尼特性相同，因此每个质量的黏滞阻尼系数均为4.5×104(N·s)/m，总和为9×104(N·s)/m。待优化参数为线性质量和非线性质量的刚度系数，优化结果见图4，最优线性质量和非线性质量刚度系数分别为3×106N/m和5×108N/m3(图中圆点所示)。

一型NES和TMD各有1个待优化参数，为各自刚度系数。优化后一型NES的刚度系数为3×108N/m3，TMD刚度系数为3×106N/m。

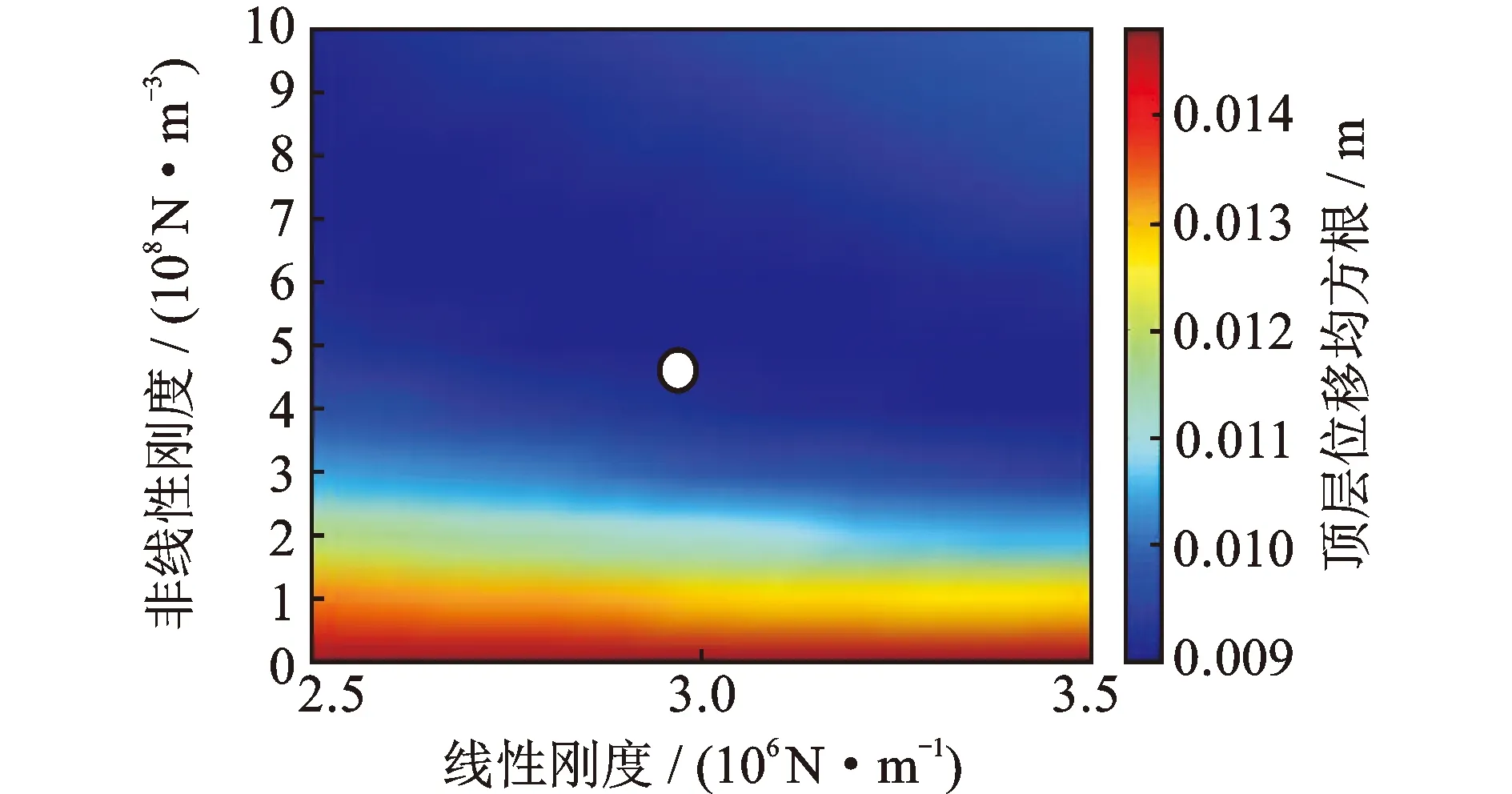
图4 双联刚度优化结果

3 脉冲型响应分析

3.1 能量鲁棒性

图5对比了在优化脉冲型荷载(其初始速度为0.25m/s)作用下无控系统、TMD系统、一型NES系统、单联系统以及双联系统的顶层位移响应。通过对比可知，4类质量阻尼器经过优化后具有极强的减振性能，在4个周期内(约3s)可将位移降至其最大值的1/4以下，四者控制能力相当。

图5同时考察当减小和增大脉冲型荷载时及主体结构基本频率降低25%时各控制装置的减振效果，即对输入能量大小变化和频率变化的鲁棒性。当作为激励的初始速度降至0.12 m/s时，TMD系统和双联系统减振性能与优化荷载时相比几乎没有变化，其中TMD系统为完全线性系统，响应变化和减振比例不受荷载大小影响。而一型NES系统与单联系统控制性能明显退化，其中一型NES由于非线性更强，对输入能量依赖更大，响应也较单联系统更大。考虑到荷载减小时，无控系统本身响应很小，且一型NES和单联仍具备一定的减振能力，不会对结构安全造成过大影响。当初始速度升至0.5 m/s时，可以观察到与0.12 m/s初始速度时相似的情况，不同的是，此时一型NES系统和单联系统响应在约5 s时已减至与TMD系统和双联系统相近的水平，且此后响应仅存在微小幅值的振动。

图5 原频率和变频率系统在不同初始速度时顶层位移

3.2 频率鲁棒性

降低主体结构频率可用于模拟结构因发生破坏刚度下降所导致结构特性的变化[18]。当主体结构基本频率降低25%时，TMD与主体结构不再调谐，不能有效形成共振机制而导致控制能力退化。可观察到，在3种初始速度作用下，TMD系统响应接近无控系统，在4种方法中控制性能最弱。当初始速度为0.25和0.5 m/s时，一型NES减振能力最强，这是由于输入能量使附加质量产生足够的回复力，此时控制装置的非线性越强越能适应主体结构频率的变化。而在0.12 m/s初始速度作用下，非线性程度越大的质量阻尼器等效线性刚度越小，产生的回复力也远小于线性程度更大的质量阻尼器，因此一型NES系统的响应大于两类联合阻尼器系统的响应。在两类联合阻尼器中，单联较双联控制能力更强，结合主体结构频率无变化时的响应可知，两者中单联更接近一型NES，频率鲁棒性更强，双联更接近TMD，能量鲁棒性更强。

4 地震响应分析

为考察各类质量阻尼器在地震作用下的控制性能，笔者对Pacific Earthquake Engineering Research Center(PEER)网站[19]下载的7条实测地震波作用下的结构响应进行了分析，表1列出了7条地震记录的特性，地震峰值加速度(peak ground acceleration，简称PGA)范围为0.47 m/s2(1号)至2.34m/s2(7号)。地震加速度的大小对应输入结构的能量大小，各控制装置在不同峰值加速度地震作用下的减震性能可在一定程度上反映其能量鲁棒性。同时，考虑到各地震波频率成分各异，主体结构频率的轻微变化有可能激发地震响应的巨大改变，因此笔者还对主体结构频率下降25%时各系统的减震性能，即频率鲁棒性进行了考察。表1同时列出了各地震作用下无控系统在原频率时和频率下降25%时的顶层位移峰值。

表1 地震记录特性及无控系统响应

Tab.1 Earthquake properties and responses of uncontrolled system

编号地震PEER编号持时/sPGA/(m·s-2)无控系统/mm原频率75%频率1KernRSN13_KERN_PAS18077.250.4727.4339.712KernRSN13_KERN_PAS27077.350.5254.2447.553KernRSN12_KERN_PEL_PEL18070.000.5835.2959.084LomaprietaRSN736_LOMAP_A0922739.051.0350.20129.735TabasRSN138_TABAS_BOS-L135.001.0362.6250.596LomaprietaRSN737_LOMAP_AGW00060.001.6640.9166.907LomaprietaRSN739_LOMAP_AND34039.752.3455.0761.55

图6绘制了原频率时各控制系统与无控系统顶层位移峰值和均方根的比值。如图所示，在主体结构频率保持不变时，各控制装置均可达到较好的减震效果，其中3号、7号2条地震作用下，各控制系统与无控系统的响应比值均在0.6以下，减震效果显著。4种控制方法中，一型NES由于非线性最强，能量鲁棒性较差，在能量各异的地震作用下减震性能较其他方法较弱。当不考虑一型NES系统时，除以上提到的2条地震外，TMD系统、单联系统和双联系统还在1号、2号、5号和6号等4条地震作用下响应均方根比值小于0.6或略超过0.6。两类联合控制方法响应峰值与TMD接近，在大多数地震作用下减震性能与TMD相当。

图6 原频率系统在地震作用下顶层位移峰值(左)与均方根(右)比值

图7 3号和4号地震作用下各系统的顶层位移

图7显示了3号和4号地震作用下各系统的顶层位移响应时程。由于地震持时较长，前后段结构响应微小，图中时程只截取了响应显著的时间区间。对应图6可知，4号地震作用下各控制方法减震性能接近，3号地震作用下TMD系统和双联系统响应明显小于一型NES系统和单联系统。这种差异可以通过输入能量大小进行解释，由优化荷载作用下各系统位移响应(图5)可知，无控系统顶层位移峰值约为0.05 m，4号地震作用下，无控系统顶层位移峰值与之接近，即此时输入能量适中，带有非线性的控制方法减震性能与线性控制方法相当。而3号地震作用下，无控系统顶层位移峰值远小于优化时的响应峰值，非线性较强的控制方法，尤其是一型NES的等效线性刚度与主体结构刚度相差较大，无法有效形成共振机制，减震性能不如线性控制方法。

图8显示了7条地震作用下，当主体结构频率下降25%时TMD系统、一型NES系统、单联系统和双联系统与无控系统的顶层位移峰值比值和均方根比值。此时减震性能的整体趋势表现为TMD在所有控制方法中退化最为严重，除4号、5号、6号地震作用下TMD系统均方根响应与其他控制系统接近以外，在剩余的4条地震作用下，TMD系统的均方根响应明显大于其他控制系统响应，甚至超过对能量最为敏感的一型NES系统，原因为TMD与频率下降的主体结构不再调谐，控制性能显著减弱。综合原频率和变频率时的结构响应可知，同时具有线性和非线性特点的单联和双联较TMD和一型NES能够更好地兼顾输入能量和主体结构频率的变化，通过脉冲型荷载优化得到的控制装置在地震作用下亦展现出优越的减震性能。

图8 变频率系统在地震作用下顶层位移峰值(左)与均方根(右)比值

5 频谱分析

5.1 地震反应谱分类

由地震响应可以看出，不同地震作用下各控制方法的减震性能存在差异，对于同一种控制方法，减震效果也存在较大区别。通过分析图6中原频率时各控制系统的响应比值得到，TMD在大多数地震作用下减震效果优于具有非线性特点的控制装置，尤其是完全非线性的一型NES，这是由于TMD的线性特点使其控制性能不受响应大小的限制。但在6号和7号地震作用下，一型NES和两类联合质量阻尼器系统的响应峰值均小于TMD系统。图9根据这一特点绘制了在结构自振频率附近的地震位移反应谱，反应谱图中同时还对无控系统的第1阶自振频率(1.176 6 Hz，图中粗实线)和TMD系统的第1、第2阶自振频率(1.056 9 Hz和1.336 2 Hz，图中粗虚线)进行了标注。主体结构附加质量后自由度增加，原第1阶频率变为原频率上下的2阶频率，高阶频率变化不明显。对于完全非线性的一型NES和具有部分非线性的两类联合质量阻尼器，由于自振频率可变，附加装置后结构的第1、第2阶频率变化介于无控系统和TMD系统频率之间。图9(a)中绘制了以上提到的2条地震(带有非线性的质量阻尼器减震性能较好)的位移反应谱，反应谱呈现斜坡特点，无控系统第1阶频率处响应明显小于TMD系统第1阶频率处响应。图9(b)绘制了除此之外的5条地震(TMD减震性能较好)的位移反应谱，反应谱呈一字型，在所示频率范围内响应变化较平缓。绘制时对反应谱进行了归一化处理，即增大或缩小各反应谱使其均值为1，以便更清楚地观察各条地震的频谱规律。

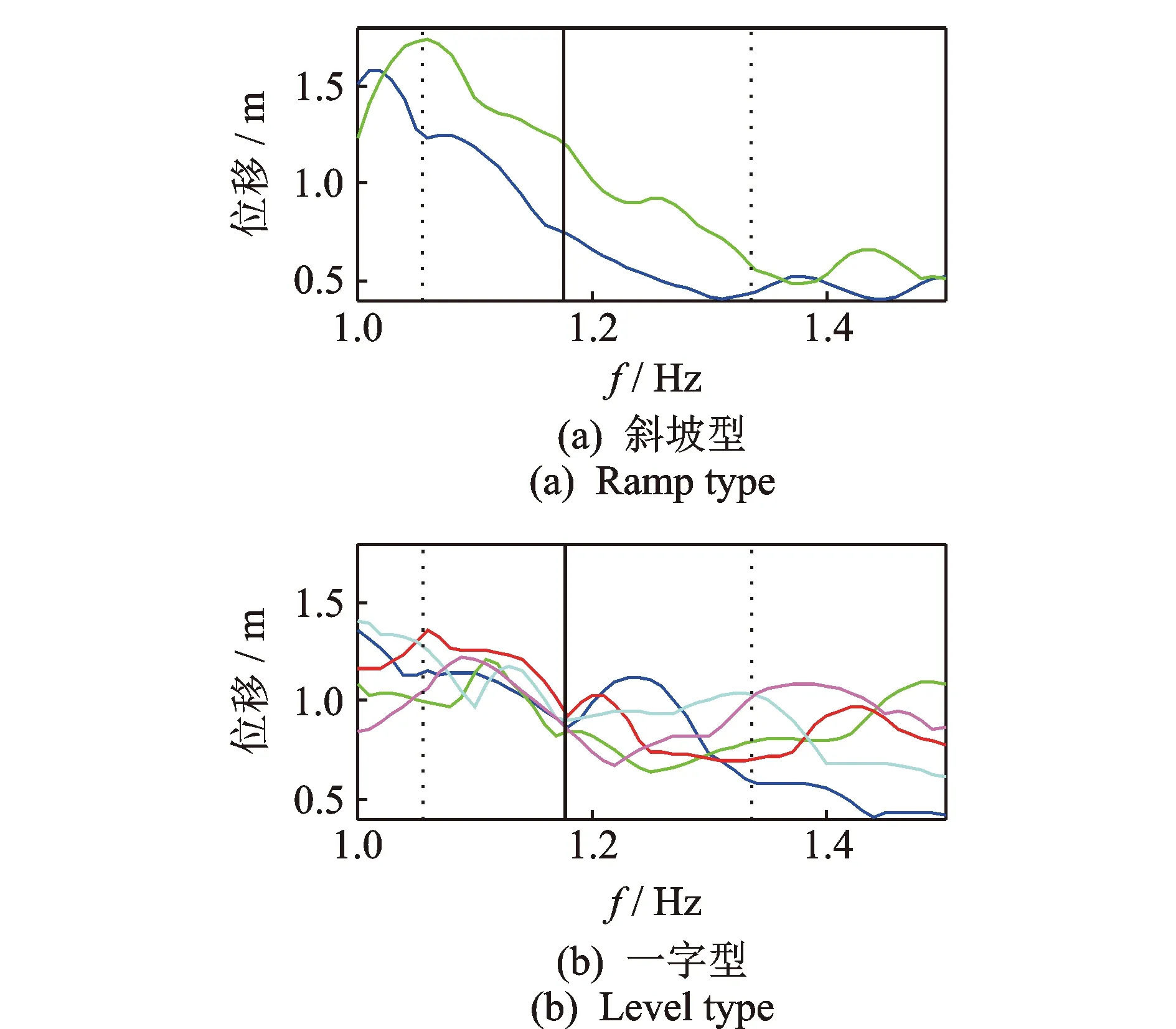
图9 斜坡型及一字型地震位移反应谱

5.2 频率成分分析

上述地震反应谱与不同控制方法减震性能之间的规律可通过对位移响应做频率成分分解进行解释。将整个频谱划分为3个部分：小于1.1 Hz(第1部分)、1.1～1.25 Hz(第2部分)和大于1.25 Hz(第3部分)，各部分频谱划分标注于图10中。无控系统第1阶频率属于第2部分，TMD系统第1、第2阶频率分别属于第1和第3部分。图10对优化脉冲型荷载作用下原频率时各系统的顶层位移响应按3个部分频率范围进行分解，并选择耗能效率最高的2.5～5 s进行对比。无控系统以其第1阶频率振动，因此可观察到第2部分频率成分显著大于第1、第3部分。TMD系统与无控系统相比第1、第3部分频率成分增加，与其第1、第2阶自振频率对应。带有非线性的控制系统中，第2部分频率成分最多，第1部分频率成分较小，且非线性程度越高(如一型NES)第1部分频率成分越小，单联系统的频率成分分布更接近一型NES系统，双联系统更接近TMD系统。根据各部分频率成分对总响应的贡献可知，在各控制系统中，线性系统的响应大小主要依赖于第1和第3部分地震反应谱的大小，非线性系统的响应大小主要依赖于第2和第3部分地震反应谱的大小。对于图10所示的斜坡型反应谱，第1部分频率范围对应的位移响应大于第2部分，因此TMD系统响应大于非线性控制系统；而对于图10所示的一字型反应谱，各部分频率范围对应的位移响应差别较小，此时地震作用的输入能量大小是影响各控制方法减震性能的主要因素。

图10 各系统位移响应频率成分

图11为各系统结构响应在无控系统第1阶频率附近的小波变换图。小波变换图中阴影深浅对应振动的大小，各控制系统小波阴影明显浅于无控系统，即振动显著小于无控系统。图11还对无控系统第1阶频率和TMD系统第1、第2阶频率位置进行了标注。无控系统与TMD系统为线性系统，小波图中所示振动主要集中在各自自振频率处。一型NES系统为完全非线性系统，振动无明显固定频率，部分集中于无控系统第1阶频率处，且向高频区域延伸。单联系统与一型NES系统接近，但低频区域振动略大于一型NES系统。双联系统中可以观察到2个频率处的振动，其中较高频振动介于无控系统第1阶频率和TMD系统第2阶频率之间，是振动的主要成分。通过小波变换可验证响应频率成分分析所得到的结果，即非线性-线性联合的控制方法使系统振动频率介于TMD系统和一型NES系统之间，单联和双联兼备非线性和线性控制方法的特点。