深度学习融合模型在机械故障诊断中的应用*

王应晨, 段修生

(1. 陆军工程大学电子与光学工程系 石家庄，050003) (2. 石家庄铁道大学机械工程学院 石家庄，050003)

引 言

机械装备的故障诊断是通过其监测数据来分析装备状态的健康状况，确定是否对其进行维护。现代武器装备系统中各个部分相互耦合，故障模式复杂多样，使故障诊断具有很大的难度和不确定性，对于复杂系统快速有效的故障诊断是装备保障的重要课题。传统的智能诊断方法在机械故障诊断中得到了广泛的应用，但仍存在3个固有的缺陷：a.诊断性能很大程度上依赖于专家经验所提取特征的质量；b.在不同的诊断问题中选择敏感的特征费时费力；c.神经网络(neural network,简称NN)和支持向量机(support vector machine,简称SVM)等属于浅层学习模型，难以有效学习复杂的非线性关系。因此，有必要构建自动学习特征和精确故障诊断的深度学习架构。

为了克服浅层模型的缺点，Hinton首先提出了深度学习理论，此后深度学习引起了广泛的关注，并取得了大量成功的应用[1]。深度学习强大的非线性映射能力以及多隐含层使其与NN，SVM等浅层学习模型相比，能够更加有效、灵活地学习故障诊断问题中的复杂关系。赵光权等[2]将深度信念网络(deep belief network, 简称DBN)用于轴承的故障诊断，该模型从原始时域信号中逐层提取故障特征，输入Softmax分类器，获得了较高的诊断精度。Guo等[3]采用堆栈降噪自编码机(stacked denoising autoencoder,简称SDAE)来实现旋转机械故障诊断。采用原始数据训练模型，通过与不同级别的随机噪声结合组成新的数据进行测试，取得了较好的结果，证明了该模型在自动提取特征的同时能有效处理原始信号的噪声。这些应用仍然存在以下局限性：a.没有充分利用不同的模型来提高特征学习能力和抗干扰性；b.标准的深度学习算法存在误差振荡，收敛速度慢。

笔者提出了利用降噪自动编码器和自适应高斯深度信念网络结合提取故障特征，粒子群支持向量机(particle swarm optimization SVM,简称PSO-SVM)进行分类的诊断系统。利用不同基础模型的优点，在提取信号特征的同时进行去噪，并采用自适应学习率有效提高网络的诊断精度和收敛速度。

1 深度神经网络模型简介

1.1 降噪自编码器

降噪自编码器(denoising autoencoder, 简称DAE)是对普通自动编码器(autoencoder,简称AE)的有效改进[4]，为使AE 隐含层学习到的特征更具鲁棒性，在训练样本中加入随机噪声来污染输入数据，之后送到网络中进行编码和解码，DAE从损坏的数据来重建未损的数据，以此提高模型的抽象能力，得到对原始数据更加鲁棒的表达。

图1说明了DAE的结构与训练过程，主要目标是最小化重构误差，定义为

(1)

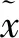
在训练过程中，DAE被迫捕获数据中的隐含不变量，在诊断经常受噪声影响的振动信号时，抵抗噪声的鲁棒性是非常重要的特性。

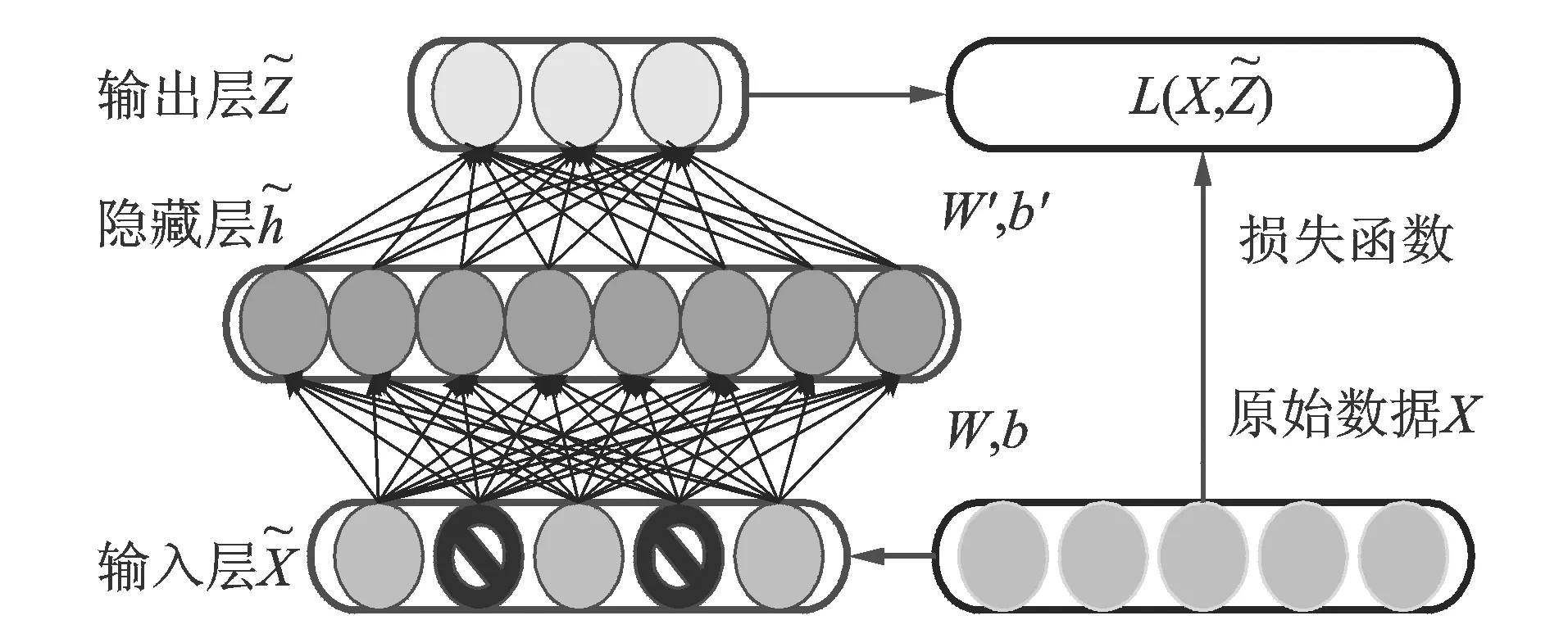
图1 降噪自编码器的编码和解码过程

1.2 高斯受限玻尔兹曼机

受限玻尔兹曼机( restricted botlzmann machine, 简称RBM) 是一个由可见层和隐含层组成的双层神经网络[5]。可见单元和隐藏单元之间存在加权连接，但是其同层节点之间无连接，见图2。

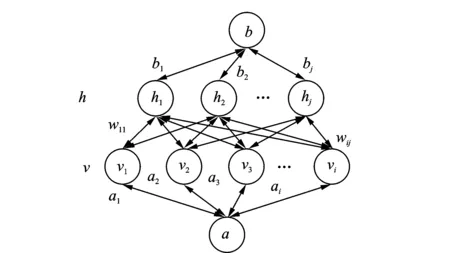
图2 RBM的结构

在RBM中，各节点是二进制值，而故障信号是连续数值。因此笔者采用了高斯受限玻尔兹曼机(Gaussian RBM, 简称GRBM)，将二进制的可视层节点值替换为具有高斯分布的连续实数，使输入层能够接受连续型信号，隐含层仍采用服从伯努利分布的二值神经元节点，GRBM的能量函数为

E(v,h;θ)=

(2)

模型参数为θGRBM={wij,ai,bj}，其中：wij为可见单元v与隐藏单元h之间的权重；ai和bj分别为它们的偏置；n和m分别为可视层和隐含层单元的数量。

基于该能量函数，得到(v,h)联合概率

(3)

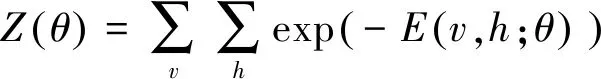
由于隐藏层和可视层内部没有连接，同层的节点间相互独立，当给定可见层单元状态v时，隐含层第j个单元hj的激活概率为

(4)

可视单元vi的激活概率为

(5)

其中：σ=1/(1+e-x)为sigmoid函数；N(μ,σ2)表示均值为μ、方差为σ2的高斯分布。

GRBM的训练采用由 Hinton[6]提出的CD 算法：从训练样本的任一状态出发，按照式(4)计算出隐含单元的概率，然后固定隐含单元，按照式(5)重构出可视单元。这样,得到模型参数θGRBM={wij,ai,bj}的近似调整规则

其中：〈·〉data为由样本数据决定的期望；〈·〉recon为重构数据的期望；ε为学习率。

训练样本一般被分为多个小子集，每个子集训练完成后，再更新模型的参数。

1.3 高斯深度信念网络

高斯深度信念网络(Gaussian DBN，简称GDBN)是通过层叠几个GRBM构建的。具有3个堆叠的GRBM的GDBN体系结构如图3所示。

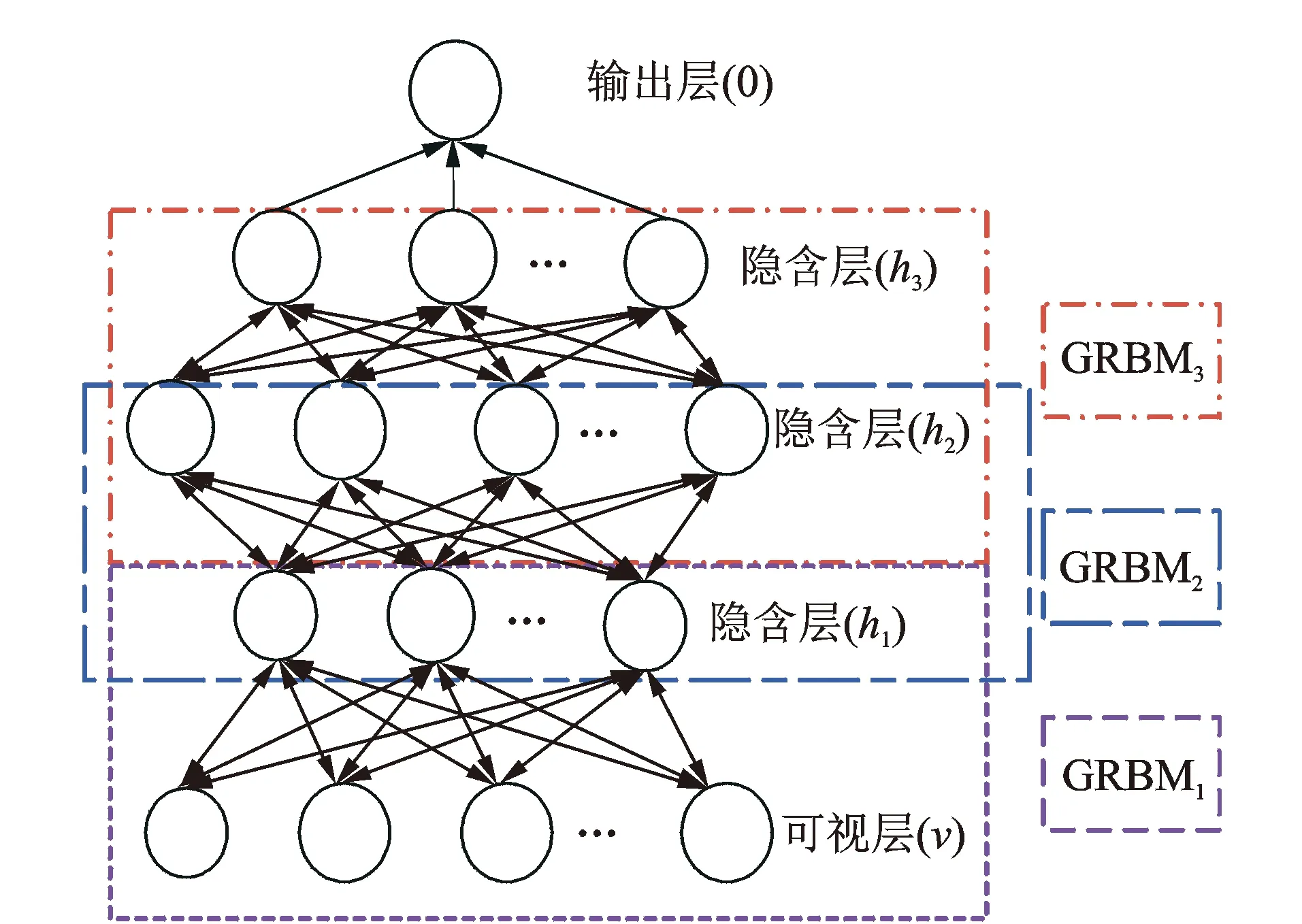
图3 GDBN结构

GDBN特征提取过程采用逐层无监督贪婪预训练[7]，将数据输入到第1个GRBM的可见层中，并使用激活函数将其转换为隐藏层，前1个GRBM学到的特征作为下1个的输入，直到最后1个GRBM，无监督预训练结束，GDBN从原始数据自动学习的特征被送入分类器中。

2 自适应学习率

学习率是影响GDBN收敛速度和提取特征性能的决定性因素[8]。标准GRBM的学习算法中采用固定的学习率来训练网络，确定后，学习率在整个训练过程中保持不变，自适应性差。如果学习率过大，很可能会越过最优值，在局部最优点附近来回跳动；而如果学习率过小，优化的效率可能过低，算法长时间无法收敛，所以学习率对于算法性能至关重要。

为了获得更好的故障诊断性能并加速网络的学习过程，在传统DBN算法基础上，引入一种基于重构误差的自适应学习率算法，可以在训练中每一步自适应调整学习速率。重构误差是RBM学习规则中应用最广泛的判断标准，定义为

(9)

可以在RBM训练规则中的每个时期调整学习速率。动态调整学习率为

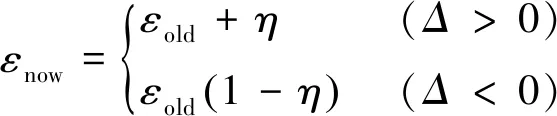
(10)

其中：η∈(0,1)为增减因子，用来调整学习率；εold为原来的学习率；εnow为更新后的学习率；Δ=Errold-Errnow。

对比连续的重构误差Errnow与Errold，当重构误差减小时，加大学习率；当误差增大时，则减小学习率。

3 基于DAE和GDBN的融合模型

深层神经网络在构造时非常强调模型的混合[9]，目前的深度学习模型大都是由一些简单而相同的基本模型构建，不能同时充分利用不同基础模型的优点。为了进一步提高模型的特征学习能力，有必要结合不同深度学习模型，设计一种混合模型。受限玻尔兹曼机和自编码器是构成深度神经网络的基本单元，文献[10]指出，自编码器擅长于扩充数据，而受限玻尔兹曼机擅长投影数据，并基于此提出了基于DBN和SAE的融合模型，较好地解决了作曲家分类问题，也证明了参数传递在自编码器和深度置信网络这两个模型间是可行并有效的。

降噪自编码器可以从损坏的输入中学习有用的信息并从隐含层重建干净的数据，具有保持原始数据的可恢复性的作用，这对于初级特征的提取非常重要[10]。对于第1层网络，原始数据被映射到一个高维的空间能够增加数据的可分性，并且在这个投影过程中数据的可恢复性能够确保投影结果的相对稳定性，而RBM投影的结果依赖于隐节点的概率分布[10],因此网络的第1层由降噪自编码器来构建，学习原始振动数据的鲁棒重构。

笔者结合DAE和DBN的优势进一步提高特征学习能力，DAE用于处理原始信号的随机噪声并学习低层特征，DBN用于基于所学习的低层特征来学习深层特征。

4 基于深度学习融合模型的故障诊断方法

诊断模型以降噪自动编码器和自适应高斯深度信念网络来提取故障特征，利用PSO-SVM作为分类器，如图4所示。

图4 改进的故障诊断模型

其步骤如下：

1) 利用传感器采集装备在不同故障状态下的监测信号；

2) 对采集到的数据进行等分样本段后线性归一化，划分训练集和测试集，对模型进行训练；

3) 建立单隐层的DAE对输入数据提取低层故障特征；

4) 将DAE的隐含层作为第1个GRBM的可视层，建立多隐层自适应高斯深度信念网络，无监督逐层预训练，提取故障深层特征；

5) 将深度网络提取到的故障特征输入PSO-SVM进行训练，得到训练好的诊断模型；

6) 将测试集数据输入训练好的模型，输出识别结果，完成故障诊断。

5 实例分析

滚动轴承是机械装备的核心部件，其健康状况对装备的机械性能、稳定性和寿命有重要的影响。笔者通过轴承故障诊断实验来验证所提算法的机械故障特征提取及诊断能力。

5.1 仿真信号描述

振动信号通常包含大量的信息，因此，基于振动信号的状态监测技术已被广泛应用。凯斯西储大学(CWRU)轴承数据中心以12 kHz采样频率从电机驱动机械系统的加速度计获得的轴承状态数据集有以下4种故障类型：正常、球故障、内圈故障和外圈故障，每种故障类型分别包含0.177 8，0.355 6和0.533 4mm这3种故障直径，共有10个故障条件。将采集的振动信号以相等的窗口长度划分，每个样本包含1 024个数据点，数据集A，B和C分别包含不同负载下的70个训练样本和30个测试样本，数据集D包含所有3个负载的210个训练样本和90个测试样本。将这些时域振动信号的频谱直接作为特征向量来表示轴承的故障类型，数据集的每个样本都包含512个样本点。表1描述了所有数据集的细节,其中： RF，IF和OF分别代表滚珠、轴承内圈和外圈故障；RF1～RF3代表不同的故障深度。

5.2 实验步骤

1) 原始数据是512维的，所以DAE输入层节点数为512，隐含层将原始数据映射到高维度的空间，实验得到最优节点数为两倍空间即1 024左右；将DAE的隐含层作为GDBN第1个GRBM的可见层，之后依次通过节点数为500和300的隐层对数据进行压缩，提取深层特征。DAE噪声系数取0.5，经反复实验得到自适应学习率增减因子最优值η=0.7，训练迭代次数为100。

表1 轴承故障数据

2) 将提取到的特征输入PSO-SVM，初始化PSO参数为：最大进化代数为200，种群数量为20，学习因子c1为1.5，学习因子c2为1.7，训练和测试模型；

3) 为了验证所提方法的优越性与鲁棒性，将本研究方法与标准GDBN、标准SDAE、自适应GDBN在相同的网络结构和PSO-SVM参数下的诊断精度进行对比，标准GDBN学习率为1，DAE噪声系数取0.5。

5.3 仿真结果分析

5.3.1 特征提取能力分析

为了观察深度学习的特征提取能力，利用非线性降维算法(t-distributed stochastic neighbor embedding, 简称t-SNE)将笔者所提融合模型学习到数据集A的故障特征转换映射，显示为二维散点图，分别命名为t-SNE1和t-SNE2，见图5～图7。

可以看出，提出的模型能够对不同故障深度和故障类型的数据进行较好的特征提取，并且各原始特征点似乎是同心圆，经过深层学习模型后被线性分割，这展现深度学习强大的非线性映射能力。

5.3.2 收敛性分析

在实践中通常用平均重构误差来表示RBM对原始输入数据的似然度，并反映训练过程中收敛速度的快慢。图8给出了自适应学习率和固定学习率性能的对比。

可以看出，ε=1时重构误差一开始呈现急速下降趋势，引起了算法不稳定；ε=0.5时收敛速度较慢；采用自适应学习率时，迭代到第20次时已基本达到稳定 并且重构误差最小，证明了所提出的自适应策略在提高收敛速度和重构精度方面的有效性。

图5 原始数据特征分布可视化

Fig.5 Visualization of the raw data via t-SNE

图6 DAE提取低层特征分布可视化

Fig.6 Visualization of the Low-level feature dis-tribution extracted by DAE via t-SNE

图7 GDBN提取深层特征分布可视化

Fig.7 Visualization of the Deep-level feature dis-tribution extracted by GDBN via t-SNE

图8 最后1个RBM的重构误差

Fig.8 Reconstruction error of the last RBM

5.3.3 故障诊断能力分析

利用各诊断模型分别进行10次实验，取最好的1次测试结果表征模型的诊断精度。图9具体显示了本研究方法在数据集A的每个故障状态的识别准确度，数据集A的训练集全部被正确识别，测试集的两个样本识别错误。

表2为4种不同方法在4类数据集下的测试结果。分析得出，4种方法的诊断时间相差不多，这是因为4种方法的特征提取网络结构和分类器都比较相似，处理的时间也相近。在不同的负载下笔者提出的融合模型的诊断精度都高于其他3种传统模型，并且自适应GDBN的性能优于标准GDBN。

图9 训练结果与测试结果

表2 不同模型的诊断结果

5.3.4 鲁棒性分析

为了验证所提方法处理随机噪声的能力，进一步证明所提出方法的优越性，实验中模型由原始数据进行训练，然后对含噪声的数据进行测试。数据集A的信号在时域中与加性高斯白噪声合成不同信噪比的信号，并在此之后转换为频率信号，定义为

(11)

其中：Psignal和Pnoise分别为信号功率和噪声功率。

图10 给出了信号与噪声混合示例。

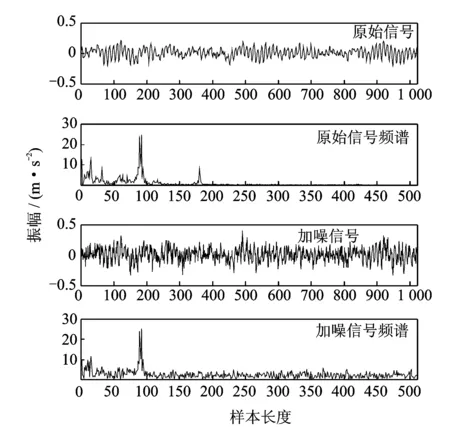
图10 信噪混合示例

噪声信号范围为-4～10 dB，比较本方法与自适应GDBN、标准SDAE，图11显示了不同噪声干扰水平下3种模型的故障识别精度，可以看出所提方法略优于SDAE。与传统GDBN相比，随着噪声水平的增加，所提方法的优越性变得明显，表明该方法对一定范围的噪声水平具有鲁棒性。

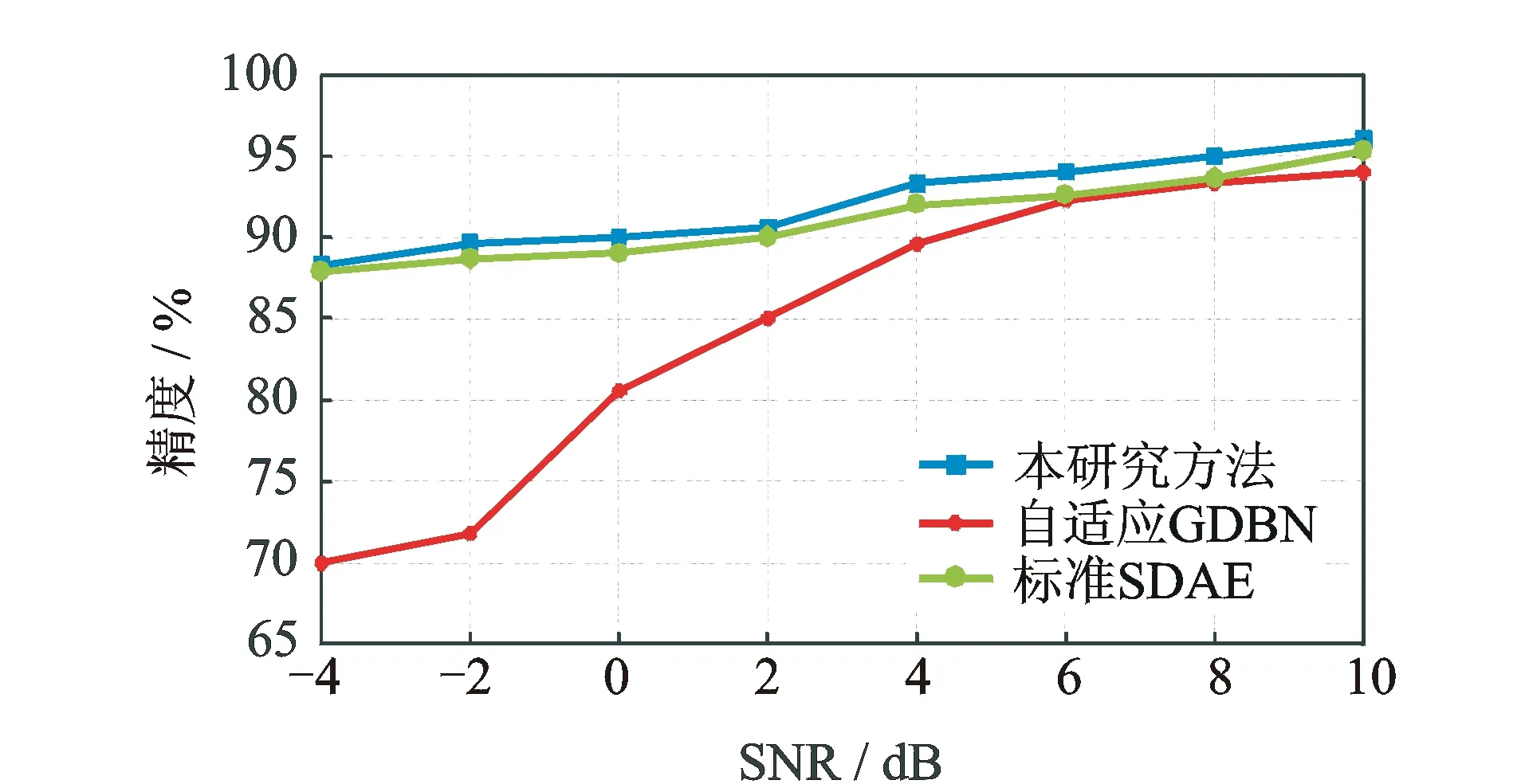
图11 不同模型在不同噪声环境下分类精度

6 结束语

提出了一种基于降噪自编码器和自适应高斯深度信念网络的深度学习融合模型来解决机械装备故障诊断问题。该模型直接处理原始振动信号，无需耗时的手工特征提取过程，并采用自适应学习率提高了网络的收敛速度和诊断精度，优于传统单一的深度学习模型，并且在噪声环境下工作良好。