模态辨识中随机减量技术的实用改进*

陈太聪， 沈文杰

(1. 华南理工大学亚热带建筑科学国家重点实验室 广州，510641)

(2. 华南理工大学土木与交通学院 广州，510641)

引 言

在工程结构的健康监测实践中，结构模态参数识别是关键工作之一。针对环境激励下的结构工作模态辨识问题，人们已发展了多种分析方法。其中，Cole[1]提出了从系统平稳随机响应中提取自由振动衰减历程的随机减量技术(random decrement technique，简称RDT)。由于RDT计算量小，处理速度快，应用成本低，易于在线实现，因此在工程实践中得到了广泛应用[2-3]。

传统RDT主要通过位移或速度响应数据来获取结构自由振动衰减响应曲线[4]，继而可采用基于自由振动响应的Ibrahim时域方法[5](Ibrahim time domain method，简称ITD)进行模态辨识。工程实践中针对加速度响应的测量较为常见，此时RDT所得的加速度特征信号存在奇异值[6]，与自由振动衰减响应曲线不符，若直接用于ITD将会导致结构模态参数的有偏估计和结果异常[7]，影响RDT的实用性。近年来有学者针对基于加速度响应的随机减量技术开展研究，如：Huang[8]结合自回归模型(auto regression，简称AR)时域算法；Ku等[9]结合频响函数(frequency response function，简称FRF)频域算法；Areemit等[10]结合特征系统实现(eigensystem realization algorithm，简称ERA)时域算法，都可以较好地求解模态参数，但结合ITD的时域算法研究仍较为少见。此外，在多自由度系统的模态辨识实践中，无论采用何种响应数据，由于识别算法和测量噪声的影响，常常得到复模态结果。此时对于经典阻尼结构，需要从识别所得复模态中提取结构实模态，而传统的模数方法[11]和最大关联度法[12]仍不具有广泛的适用性。

针对传统RDT+ITD方法在工程结构工作模态分析实践中存在的问题，笔者开展相关研究，以实现基于不同响应数据的RDT+ITD用于一般多自由度系统的模态辨识，改善辨识效果。首先，针对随机减量加速度特征信号存在的奇异值问题，提出加速度特征信号截断方法，探讨有效的截断比例取值，截断后可直接应用于ITD进行模态辨识；其次，针对多自由度结构模态辨识中的复模态结果，提出最小距离法用于经典阻尼结构的实模态提取，并在响应数据适应性和抗噪性两方面，与传统的模数方法和最大关联度法进行对比；最后，通过3自由度结构算例和桁架模型实验，对所提方法进行验证。

1 RDT+ITD模态辨识基本原理

1.1 随机减量特征信号的构造

RDT处理是将随机响应过程转化为随机减量特征信号的过程。对于平稳随机过程X(t)和Y(t)，随机减量特征信号定义为在一定条件T下随机过程的一个均值。该信号的数学表达可描述为

δYX(τ)=E[Y(t+τ)|TX(t)]

(1)

其中：δYX(τ)的第1个下标Y表示均值来源的随机过程；第2个下标X表示条件T来源的随机过程。

在RDT的实际应用中，测试所得的结构动态响应时程只是随机过程的一个样本实现过程，因此，在假设随机过程是平稳且遍历的前提下，随机减量特征信号可表达为该样本过程的条件均值

(2)

式(2)中的触发条件T可以有多种形式，包括水平穿越触发、零穿越触发、极值点触发和随机采样触发等。以常用的水平穿越触发条件为例，随机减量特征信号由下式计算

(3)

对于多自由度系统，RDT处理[13]如下：选取1个测点的响应通道作为参考通道，对该响应通道做单自由度系统下的RDT处理，即截取若干个子信号段进行总体平均；同时记录下每个子信号段截取的时刻，根据这些时刻对其他测点的响应通道作相同的总体平均处理，从而得到每个测点的随机减量特征信号。

1.2 基于自由振动衰减信号的模态辨识

ITD方法的基本计算原理可概括如下。

在等时距测量情况下，第t时刻的结构自由振动观测响应X(t)可由观测模态ψr叠加表达为

(4)

其中：ωr为结构固有频率；μr=exp(ωrΔt)。

若构造两组观测矩阵

(5)

(6)

则结合式(4)可得

D=ΦΛ

(7)

(8)

其中

(9)

由式(7)及式(8)消去Λ后，可得

(10)

令

(11)

则由式(10)可知

A=ΦΩΦ-1

(12)

(13)

其中

(14)

在求得μr和Φ后，结构系统的第r阶固有频率ωr和阻尼比ζr可分别确定为

ωr=|lnμr|/Δt

(15)

(16)

2 实用改进技术

2.1 随机减量加速度特征信号截断

若外激励是零均值的平稳高斯白噪声，则由水平穿越触发条件构造得到的随机减量特征信号，与随机响应相关函数RYX(τ)之间有如下对应关系[6]

δYX(τ)=RYX(τ)x0/RYX(0)

(17)

以单自由系统为考察对象，将平稳随机振动理论的随机响应相关函数表达式[14]代入式(17)中，可以解得具体的位移、速度和加速度响应对应的随机减量特征信号表达式分别为

(18)

(19)

(20)

其中：ωn和ωd分别为系统无阻尼和有阻尼自振频率；ζ为系统阻尼比；δ(τ)为狄拉克函数。

通过与以下自由振动衰减响应的对比

(21)

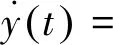
(22)

(23)

可以发现，对于位移和速度响应，随机减量特征信号等价于具有特定初始条件的自由振动响应；但对于加速度响应，随机减量特征信号与自由振动响应有所区别，其在τ=0处存在一个奇异值。

在多自由度结构的随机减量应用中，文献[6]已证明，随机减量加速度特征信号同样存在τ=0处的奇异值，其大小取决于随机激励的相关函数和结构的质量阵，因此该奇异值被应用于多维随机激励间的时延相关性检查以及结构集中质量阵的判定。

在结构模态辨识中，Ku等[7]的研究表明，随机减量加速度特征信号的奇异值会产生不利的影响，可能导致有偏估计和结果异常。为了降低该奇异值的影响，有研究在后续采用结合AR模型[8]、FRF[9]及ERA[10]等无需严格要求信号的自由振动性质的识别算法，意即对于随机减量加速度特征信号的初始奇异值不敏感，均可以获得良好的模态辨识效果。

笔者通过多个数值算例和模型实验的结果分析，综合考虑误差影响和数据完整性，使用1/200～1/50作为加速度特征信号的截断比例，即重设随机减量加速度特征信号总时程的1/200～1/50处时刻为起始时刻，可有效保证模态识别精度。

2.2 经典阻尼结构实模态提取

对于多自由度经典阻尼结构系统，识别算法和测量噪声往往导致识别得到的结构自振模态为复模态形式，而非实模态。ITD方法中的扩大模型法[15]可用于从识别复模态中提取实模态，但该方法的处理过程较为复杂，不易应用。出于实际应用的目的，多名学者提出了不同方法，其中以传统模数法和最大关联度法较为常用。

传统模数法取识别复模态φC的模作为实模态φR的大小，其符号由{φC}的实部所决定[11]

φR=sgn[Re(φC)]⊙|φC|

(24)

其中：sgn(·)为符号函数。

该方法较适用于小阻尼结构，此时的复模态相位角偏离0°或180°,约在10°以内[16]。

最大关联度法由Ahmadian等[12]给出了一般形式，应用也较为广泛[3, 17]。实模态φR由复模态φC旋转得到

(25)

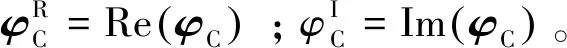
式(25)中的转角θ通过最大化复模态φC与实模态φR之间的关联度获得，即由

(26)

可解得转角θ满足条件

(27)

虽然上述两种方法的思路清晰，操作简单，但实际计算表明，两者仍不具有广泛的适用性。基于最小距离的思想，笔者提出一种新的转换方法，在复平面中使原复模态与转换实模态之间的距离最短，即寻找实模态φR和转角θ以使达到以下指标

(28)

令式(28)中的性能函数对φR和θ的1阶导数分别等于零，最终可解得

(29)

(30)

对比式(30)和式(25)可见，最小距离法与最大关联度法有一定程度的相似性，但由式(29)可推导得到，在应用最小距离法时

(31)

3 数值算例

为了验证本研究方法用于模态参数辨识的效果，取1个3自由度结构模型用于算例分析。结构运动方程为

考虑基底白噪声激励，在每一个自由度上均设置测点，整个结构共3个测点。基于等时间步长0.02s，采用Newmark-β数值积分法计算得到各测点的位移、速度和加速度响应，取进入稳态阶段后的90 000个时间步用于分析，即总时长为1 800s，并在位移、速度和加速度响应的模拟输出上均叠加3种不同水平(0%，10%，20%)的噪声作为观测响应。

分别对位移、速度和加速度观测响应进行相应RDT处理，获得对应的自由振动衰减信号。其中，选择第3自由度响应作为参考通道，选择1.5倍的响应数据标准差作为水平穿越触发条件，叠加长度为1 500单位步长，并选择1/200作为随机减量加速度特征信号的截断比例。后续采用ITD方法和3种实模态提取方法辨识结构的模态参数。

不同响应数据和不同噪声水平下结构所有3阶模态参数的识别结果如表1～表3所示，包括模态频率、频率识别误差、模态阻尼比、各阶识别模态与理论模态的置信度(modal assurance criterion，简称MAC)等。由表可得出以下结果。

1) 在无测试噪声的情况下，无论基于何种响应，均能够较好地识别出3个阶次的频率和模态，但阻尼比的识别精度相对较低。随着测试噪声不断增大，识别能力逐渐减弱。其中：采用速度响应对各阶次模态参数的识别效果较好；采用位移响应则是有利于低阶模态参数的识别；采用加速度响应有利于高阶模态参数的识别。该特点与白噪声激励下的位移、速度、加速度响应的频谱图分布规律相符。

2) 结构实模态识别中，在3种响应下，最小距离法和最大关联度法均显示出了比传统模数法更良好的辨识效果，但在高噪声的部分情况下，最大关联度法会失效，此时最小距离法仍能得到高精度的辨识结果，抗噪性能好。

为了验证本研究所提随机减量加速度特征信号截断方法的有效性，以及所提截断比例的可行性，取不同的截断比例(0，1/500～1/2)，对比分析相应的模态辨识结果。图1所示为未进行截断的随机减量加速度特征信号(此处仅列出第3自由度响应的结果，其他自由度的情况类似)。根据不同截断比例处理后的结构模态辨识结果如表4所示，其中采用最小距离法提取实模态。

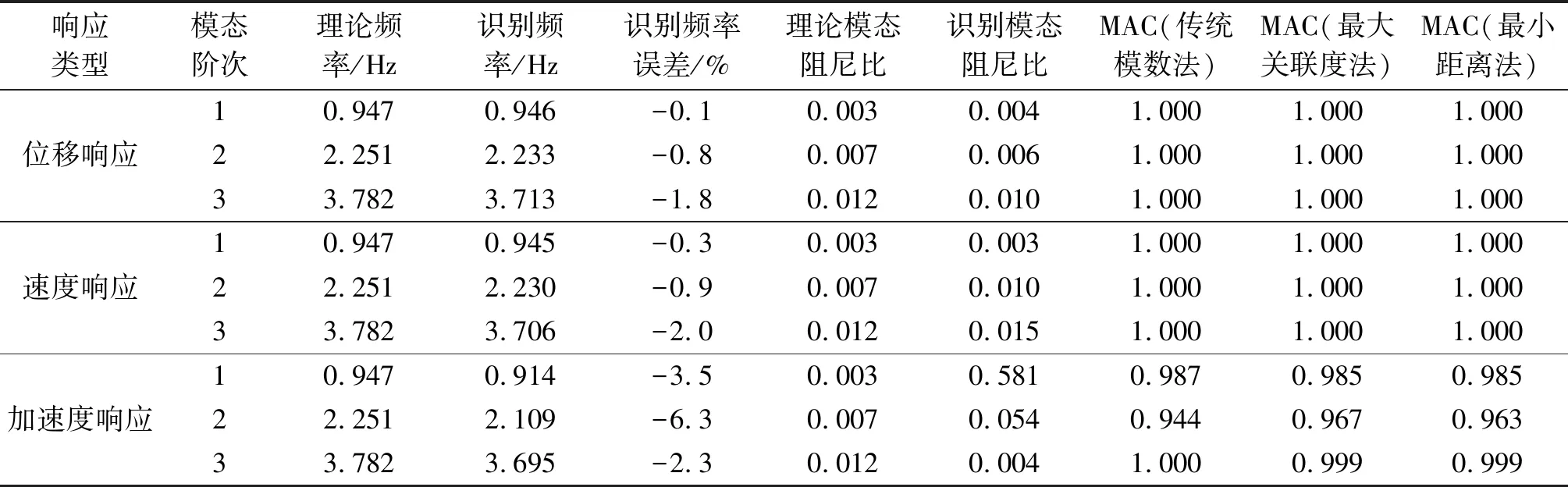
表1 RDT+ITD识别结果(噪声水平为0%)

表2 RDT+ITD识别结果(噪声水平为10%)

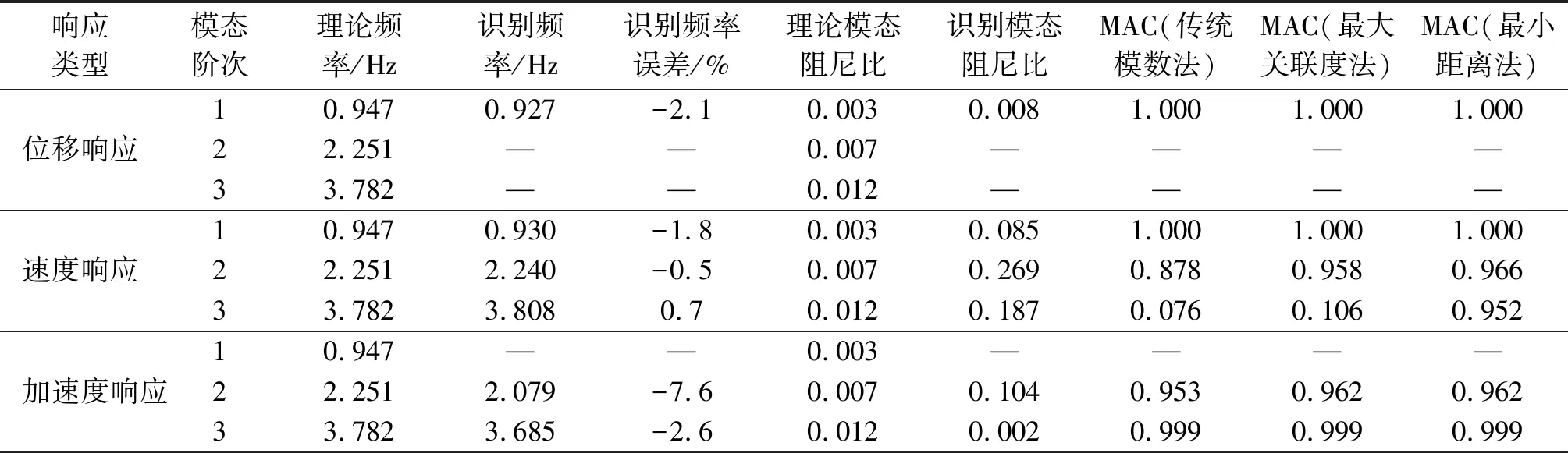
表3 RDT+ITD识别结果(噪声水平为20%)

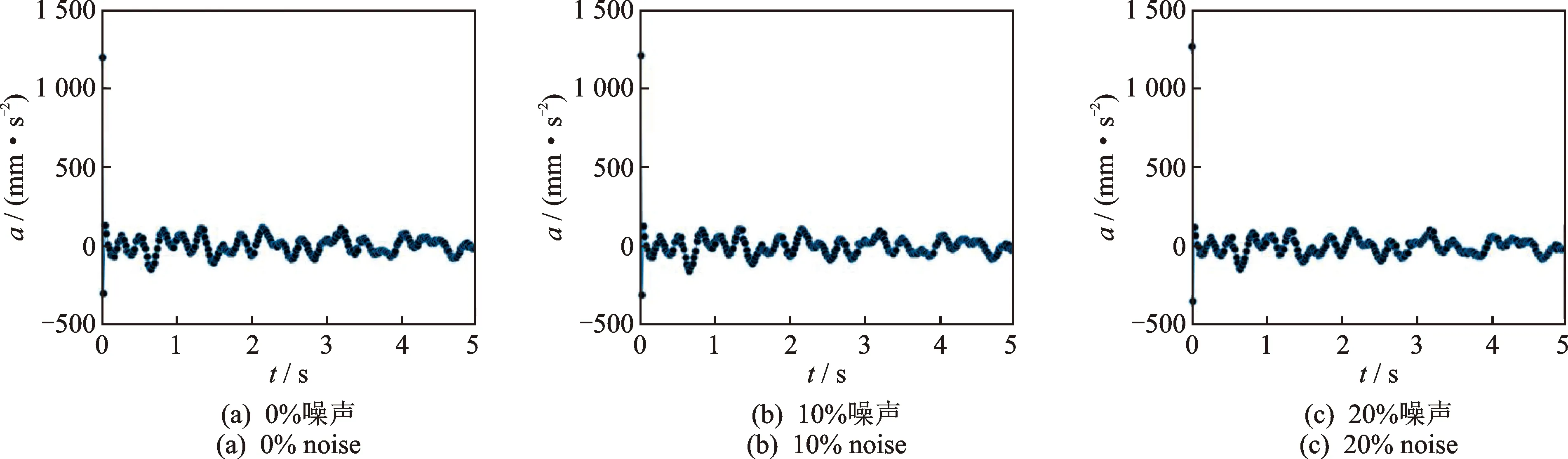
图1 不同噪声水平下第3加速度响应通道的随机减量特征信号

表4 不同截取比例下基于加速度响应的模态识别结果

由图1和表4所示结果可得：

1)τ=0附近的数据与后续数据差异较大，若不进行截断，则仅能识别得到第3阶模态，对第1阶和第2阶的有偏估计导致模态遗漏；

2) 过小的截断比例(<1/200)会导致模态参数的识别精度降低，过大的截断比例(>1/50)不仅使识别精度降低，还会导致模态遗漏；

3) 选择1/200～1/50的截断比例较能保证辨识结果的可靠性。

4 模型实验

为验证本研究方法用于实际结构模态辨识的效果，进行了桁架结构模型实验，模型如图2所示，测点编号如图3所示。在底层9号节点处施加竖向白噪声激励，进行7批次振动实验，每次测试4个测点的竖向加速度响应。其中：4号测点为多次观测的参考点；第1批测点为1～4；第2批测点为4～7；第3批测点为4，8，10和11；第4批测点为4，12～14；第5批测点为4，15～17；第6批测点为4，18～20；第7批测点为4，20～22。

分别对采集到的7批次4通道加速度响应数据进行模态辨识处理，依次将每一通道作为参考通道进行RDT处理，选择1/200作为随机减量加速度特征信号的截断比例，采用最小距离法进行结构实模态提取，最终可以得到28组模态信息。在此基础上，通过与有限元模型分析得到频率及振型对比，可确定6阶有效模态，见表5。所得结果进一步验证了针对加速度响应数据的随机减量特征信号截断方法以及针对实模态提取的最小距离法的有效性。

图2 桁架结构模型

图3 底层平面上加速度传感器的布置

为了验证所提的加速度特征信号截断比例的有效性，以第1批测试为例，取第3通道为参考通道进行RDT处理，对这组数据进行不同截断比例下的模态辨识，结果见表6。所得结果再次验证了选择1/200～1/50的截断比例用于模态辨识的可靠性。

表5 桁架结构模型的模态识别结果

表6 不同截断比例下桁架结构的模态识别结果

Tab.6 Modal identification results of truss model with different truncation ratio

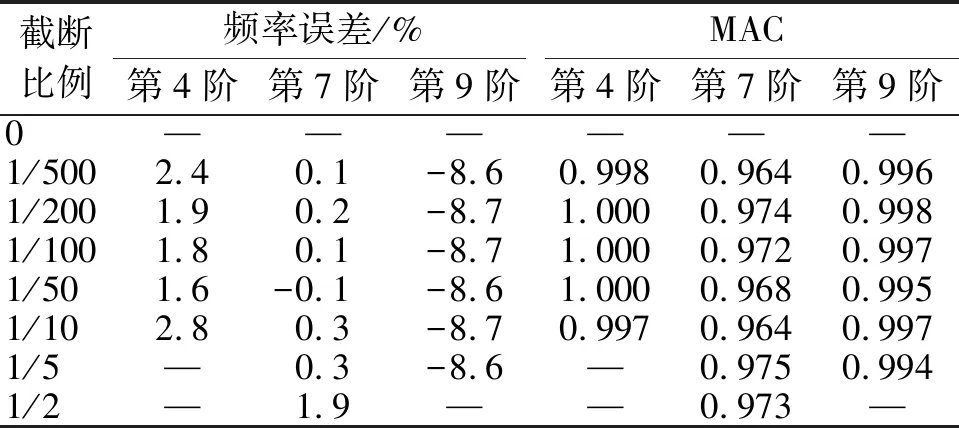
截断比例频率误差/%MAC第4阶第7阶第9阶第4阶第7阶第9阶0——————1/5002.40.1-8.60.9980.9640.9961/2001.90.2-8.71.0000.9740.9981/1001.80.1-8.71.0000.9720.9971/501.6-0.1-8.61.0000.9680.9951/102.80.3-8.70.9970.9640.9971/5—0.3-8.6—0.9750.9941/2—1.9——0.973—

5 结束语

针对传统RDT+ITD方法在工程结构工作模态分析中的应用问题，提出了随机减量加速度特征信号的截断方法，以及由识别复模态提取经典阻尼结构实模态的最小距离法，改进了基于不同响应数据的RDT+ITD用于一般多自由度系统的模态辨识效果。在对随机减量加速度特征信号进行截断时，推荐截断比例取值1/200～1/50。在提取实模态时，相对于传统模数法和最大关联度法，最小距离法对响应数据类型的适应性更强，抗噪能力更优。本研究改进方法原理简单，易于实现，可方便应用于工程振动测试实践。