统计问题中常见的典型考题赏析
2019-12-31谢红霞
■谢红霞
题型一:简单随机抽样
抽签法适用于总体中个体数较少的情况,随机数法适用于总体中个体数较多的情况。一个抽样试验能否用抽签法,关键看两点:一是抽签是否方便,二是号签是否易搅匀。一般地,当总体容量和样本容量都较小时可用抽签法。
例1完成下列两项调查:①从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户,调查社会购买能力的某项指标;②从某中学的15名艺术特长生中选出3名调查学习负担情况。宜采用的抽样方法依次是( )。
A.①简单随机抽样,②系统抽样
B.①分层抽样,②简单随机抽样
C.①系统抽样,②分层抽样
D.①②都用分层抽样
解:因为社会购买能力的某项指标受到家庭收入的影响,而社区中各个家庭收入差别明显,所以①用分层抽样法。从某中学的15名艺术特长生中选出3名调查学习负担情况,个体之间差别不大,且总体和样本容量较小,②用简单随机抽样法。
应选B。
跟踪练习1:某方便面生产线上每隔15min抽取一包进行检验,该抽样方法为①,从某中学的40名数学爱好者中抽取5人了解学习负担情况,该抽样方法为②,那么①和②分别为( )。
A.①系统抽样,②分层抽样
B.①分层抽样,②系统抽样
C.①系统抽样,②简单随机抽样
D.①分层抽样,②简单随机抽样
提示:由随机抽样的特征可知,①为等距抽样,也就是系统抽样;②为简单随机抽样。
应选C。
题型二:系统抽样
例2将参加夏令营的600名学生编号为001,002,…,600。采用系统抽样方法抽取一个容量为50的样本,且随机抽取的号码为003。这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )。
A.26,16,8 B.25,17,8
C.25,16,9 D.24,17,9
解:由题意及系统抽样的定义可知,将这600名学生按编号依次分成50组,每组各有12名学生,第k(k∈N*)组抽中的号码是3+12(k-1)。
应选B。
跟踪练习2:总体由编号为01,02,03,…,49,50的50个个体组成,利用随机数表1(以下摘取了随机数表中第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )。

表1
A.05 B.09
C.11 D.20
提示:从随机数表第1行的第9列和第10列数字开始,依次是14,05,11,09,则第四个数字是09。
应选B。
题型三:分层抽样
依据各层的个体数与样本数之比,确定抽样比;由某层个体数(或样本数)确定该层的样本数(或总体数);依据题意,求出各层的抽样比,再求出各层的样本数。
1.求总体个数或样本容量
例3某校有高级教师26人,中级教师104人,其他教师若干人。为了解该校教师的工资收入情况,按分层抽样从该校的所有教师中抽取56人进行调查,已知从其他教师中共抽取了16人,则该校共有教师人。
解:设该校其他教师有x人,则,可得x=52。故全校教师共有26+104+52=182(人)。
跟踪练习3:某工厂生产甲,乙,丙三种型号的产品,产品数量之比为3∶5∶7,现用分层抽样方法抽取容量为n的样本,其中甲种产品有18件,则样本容量n等于( )。
A.54 B.90
C.45 D.126
提示:依题意可得,解得n=90,即样本容量为90。
应选B。
2.求某层入样的个体数
例4某中学高一年级有560人,高二年级有540人,高三年级有520人,现用分层抽样的方法抽取容量为81的样本,则在高一,高二,高三这三个年级抽取的人数分别为( )。
A.28,27,26 B.28,26,24
C.26,27,28 D.27,26,25
解:根据题意可得,分层抽样的抽样比为则在高一年级抽取的人数是在高二年级抽取的人数是在高三年级抽取的人数是
应选A。
跟踪练习4:某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则分别应抽取老年人,中年人,青年人的人数是( )。
A.7,11,18
B.6,12,18
C.6,13,17
D.7,14,21
提示:因为该单位共有人数为27+54+81=162,样本容量为42,所以应按的抽样比分别从老年人,中年人,青年人中抽取样本,则分别抽取的人数是7,14,21。
应选D。
题型四:统计图表及应用
准确理解频率分布直方图的数据特点,频率分布直方图中纵轴上的数据是各组的频率除以组距的结果,不要误认为纵轴上的数据是各组的频率,不要和条形图混淆;频率分布直方图中各小长方形的面积之和为1;利用频率分布直方图可估计总体分布。
例5为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试。根据体育测试得到了这m名学生的各项平均成绩(满足100分),按照以下区间分为7组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到频率分布直方图,如图1所示。已知测试平均成绩在区间[30,60)内有20人。

图1
(1)求m的值及中位数n。
(2)若该校学生测试平均成绩小于n,则学校应适当增加体育活动时间。根据以上抽样调查数据,该校是否需要增加体育活动时间?
解:(1)由频率分布直方图可知,第1组,第2组和第3组的频率分别是0.02,0.02和0.06,则m×(0.02+0.02+0.06)=20,解得m=200。
由频率分布直方图可知,前四组的频率为0.32,第5组的频率为0.4,所以中位数n位于[70,80)内,则0.02+0.02+0.06+0.22+0.04(n-70)=0.5,解得n=74.5。
(2)设第i(i=1,2,3,4,5,6,7)组的频率和频数分别为pi和xi。由频率分布直方图可知p1=0.02,p2=0.02,p3=0.06,p4=0.22,p5=0.4,p6=0.18,p7=0.1。由xi=200×pi,可得x1=4,x2=4,x3=12,x4=44,x5=80,x6=36,x7=20,故该校学生测试平均成绩为×(35x1+45x2+55x3+65x4+75x5+85x6+95x7)=74<74.5,由此可知该校应该适当增加体育活动时间。
跟踪练习5:近年来高校招生改革的呼声越来越高,在赞成高校招生改革的市民中按年龄分组,得到的样本数据的频率分布直方图如图2所示,其中年龄在区间[30,40)内的有2500人,在区间[20,30)内的有1200人,则m的值为( )。

图2
A.0.013 B.0.13
C.0.012 D.0.12
提示:由题意可得,年龄在区间[30,40)内的频率为0.025×10=0.25,则赞成高校招生改革的市民人数为=10000。因为年龄在区间[20,30)内的有1200人,所以m=
应选C。
题型五:样本的数字特征
平均数和方差都是重要的数字特征,是对总体的一种简明的阐述。平均数,中位数,众数描述总体的集中趋势,方差和标准差描述波动大小。平均数,方差公式的推广:若数据x1,x2,…,xn的平均数为,方差为s2,则数据mx1+a,mx2+a,…,mxn+a的平均数为m,方差为m2s2。
例6某选手的7个得分去掉1个最高分,去掉1个最低分,剩余5个得分的平均数为91,如图3,该选手的7个得分的茎叶图中有一个数据模糊,无法辨认,在图中用x表示,则剩余5个得分的方差为( )。

图3

解:由茎叶图可知,最低分为87分,最高分为99分。
应选C。
跟踪练习6:若数据x1,x2,x3,…,xn的平均数为=5,方差s2=2,则数据3x1+1,3x2+1,3x3+1,…,3xn+1的平均数和方差分别为( )。
A.5,2 B.16,2
C.16,18 D.16,9
提示:由x1,x2,x3,…,xn的平均数为5,可 得所以16。由x1,x2,x3,…,xn的方差为2,可得3x1+1,3x2+1,3x3+1,…,3xn+1的方差是32×2=18。
应选C。
题型六:相关关系的判断
判断变量之间有无相关关系,一种简便可行的方法就是绘制散点图,根据散点图很容易看出两个变量之间是否具有相关性,是否存在线性相关关系,是正相关还是负相关,相关关系是强还是弱。判定两个变量正、负相关性的三种常用方法:①利用散点图,点的分布从左下角到右上角,两个变量正相关,点的分布从左上角到右下角,两个变量负相关。②利用相关系数,当r>0时,正相关,当r<0时,负相关。③利用线性回归方程,当b>0时,正相关,当b<0时,负相关。
例7当变量x的取值为3,4,5,6,7时,变量y对应的值依次分别为4,2.5,-0.5,-1,-2;当变量u的取值为1,2,3,4时,变量v对应的值依次分别为2,3,4,6。则变量x和y,变量u和v的相关关系是( )。
A.变量x和y是正相关,变量u和v是正相关
B.变量x和y是正相关,变量u和v是负相关
C.变量x和y是负相关,变量u和v是负相关
D.变量x和y是负相关,变量u和v是正相关
解:变量x增加,变量y减少,所以变量x和y是负相关。变量u增加,变量v增加,所以变量u和v是正相关。
应选D。
跟踪练习7:某中学的兴趣小组在某座山测得海拔高度、气压和沸点的6组数据绘制成散点图如图4所示,则下列说法错误的是( )。
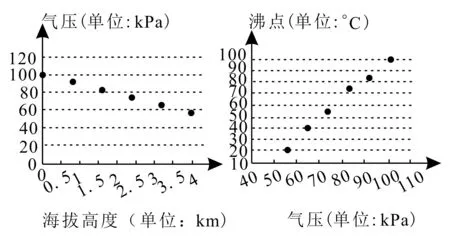
图4
A.沸点与海拔高度呈正相关
B.沸点与气压呈正相关
C.沸点与海拔高度呈负相关
D.沸点与海拔高度、沸点与气压的相关性都很强
提示:结合散点图进行判断。
由散点图可知,沸点与气压呈正相关,B正确。由气压与海拔高度呈负相关,沸点与气压呈正相关,可知沸点与海拔高度呈负相关,A不正确,C正确。结合选项B,C的说法可知D正确。
应选A。
