本期试卷参考答案

统计知识综合演练A卷参考答案与提示

一、选择题

1.提示：系统抽样就是等距抽样,被抽到的编号满足122+5k,k∈N*,可得927=122+5×161。应选A。

2.提示：根据简单随机抽样、系统抽样和分层抽样的定义可知,无论哪种抽样,每个个体被抽取的可能性(概率)都是相等的,所以p1=p2=p3。应选D。

3.提示：由表可知,最低温度大致随最高温度的升高而升高,A正确。每月最高温度与最低温度的平均值在前8个月不是逐月增加,B错误。月温差的最大值出现在1月,C正确。1月至4月的月温差相对于7月至10月,波动性更大,D正确。应选B。

5.提示：由图可知,数据落在[20,60)内的频率为(0.005+0.01)×20=0.3,可得该班的学生人数是=50。应选B。

7.提示：由频率分布直方图知,9时至10时的销售额的频率为0.1,可得销售总额为=30(万元)。由于11时至12时的销售额的频率为0.4,故11时至12时的销售额为0.4×30=12(万元)。应选C。

8.提示：由B样本数据恰好是A样本数据每个都减5后所得的数据,可得平均数,众数,中位数分别是原来结果减去5,即与A样本不相同。由标准差公式可知,标准差不变。应选B。

9.提示：已知10个数据,其中落在区间[22,30)内的数据为22,22,27,29,共4个,因此所求的频率为=0.4。应选B。

11.提示：由茎叶图可知,此组数据由小到大排列依次为76,79,81,83,86,86,87,91,92,94,95,96,98,99,101,103,114,共17个,故92为中位数,出现次数最多的为众数,即众数为86。应选B。

15.提示：以正常速度通过该处的汽车的频率为1-(0.01+0.005)×10=0.85,所以以正常速度通过该处的汽车约有0.85×2000=1700(辆)。应选D。

16.提示：根据甲班学生成绩的众数是85,得x=5;根据乙班学生成绩的平均分为81,得y=4。所以x+y=9。应选D。

20.提示：由茎叶图可知,乙运动员的成绩较稳定,其平均数为90(环),方差为2(计算略)。应选B。

21.提示：根据频率分布直方图,可得第二小组的频率是0.04×10=0.4,由频数是40,可得样本容量为=100。由成绩在80～100分的频率是(0.01+0.005)×10=0.15,可得成绩在80～100分的学生人数是100×0.15=15。应选A。

二、填空题

22.提示：设第1组抽取的号码为b,则第n组抽取的号码为8(n-1)+b,所以8×(16-1)+b=126,解得b=6。故第1组抽取的号码为6。

23.提示：中位数是13。根据统计资料可以看出,当年平均收入增多时,年平均支出也增多,因此两者之间具有正相关关系。

24.提示：根据题意可知,样本中参与跑步的人数为200×=120,所以从高二年级参与跑步的学生中应抽取的人数为120×

26.提示：由频率分布直方图可知,质量指标值在[185,215)内的频率为(0.022+0.033+0.024)×10=0.79,故该企业这种产品在这项指标上的合格率约为0.79。

27.提示：因为样本容量为20,所以样本间隔为100÷20=5。首个号码为003,样本中对应的号码数为3+5(x-1)=5x-2。

由48≤5x-2≤81,得10≤x≤16.6,即得x=10,11,12,13,14,15,16,可知被抽中的人数为7。

三、解答题

28.提示：(1)由频率分布直方图可知,分数在[50,60]内的频率为0.008×10=0.08。

由茎叶图可知,分数在[50,60]内的频数为2,所以全班人数为

(2)分数在[80,90]内的频数为25-2-7-10-2=4,可知频率分布直方图中[80,90]内的矩形的高为

30.提示：(1)由散点图知,这些点大致分布在一条曲线附近,选择回归类型y=c·xd更适合。

(2)对y=c·xd两边取对数,可得lny=lnc+dlnx,所以v=lnc+du。

31.提示：(1)分数在[120,130)内的频率为1-(0.1+0.15+0.15+0.25+0.05)=1-0.7=0.3。

(3)由题意可得[110,120)分数段内的人数为60×0.15=9,[120,130)分数段内的人数为60×0.3=18。

由用分层抽样的方法在分数段为[110,130)内的学生中抽取一个容量为6的样本,可得在[110,120)分数段内抽取的人数为6=2,分别记为m,n;在[120,130)分数段内抽取的人数为×6=4,分别记为a,b,c,d。

设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A,则基本事件为(m,n),(m,a),(m,b),(m,c),(m,d),(n,a),(n,b),(n,c),(n,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),共15种情况,其中事件A包含9种情况。

统计与算法初步综合演练B卷参考答案与提示

一、选择题

1.提示：任何一个算法都离不开顺序结构。应选D。

2.提示：二进制数是“逢二进一”,所以1010(2)+10(2)=1100(2)。

应选B。

3.提示：变量赋值的语句必须是左边为一个变量,右边为代数式。

应选D。

4.提示：由该算法程序知,最后一次运算为i=7,s=2×7+1=15。

应选C。

5.提示：先将2赋给A,再将3×2=6赋给A,最后将9+6=15赋给A。

应选B。

以此类推,可知s的值是以3为周期出现的,结束时i=2017=3×672+1,此时s=2。应选C。

7.提示：系统抽样的特征是数据多,抽样间隔相等,A正确。线性回归直线^y=bx+a一定过样本中心点),B正确。两个随机变量的线性相关性越强,则相关系数|r|越接近于1,C错误。一组数据1,a,3的平均数是2,可得a=2,该组数据的方差为s2=[(1-2)2+(2-2)2+(3-2)2]=,D正确。

应选C。

应选C。

9.提示：由题设知,若m=6,则在第7组中抽取的号码的个位数字与13的个位数字相同,而第7组中数字编号依次为60,61,62,63,…,69,故在第7组中抽取的号码是63。

应选A。

10.提示：对于①,个体没有差异且总数不多,可选用简单随机抽样。对于②,将总体分段,在第1段内采用简单随机抽样确定一个起始编号,在此编号的基础上加上分段间隔的整数倍即为抽样编号,因此属于系统抽样。对于③,个体有明显差异,可选用分层抽样。应选A。

应选A。

二、填空题

12.提示：由程序知,最后一次运算为i=9,s=2×9+3=21。

答案为21。

13.提示：设年龄在[25,30)内的志愿者的频率是p,则5×0.01+p+5×0.07+5×0.06+5×0.02=1,解得p=0.2,故估计这800名志愿者年龄在[25,30)内的人数是800×0.2=160。

答案为160。

14.提示：平均数为35×0.1+45×0.1+55×0.5+65×0.2+75×0.05+85×0.05=56.5,即平均运动时间大约是56.5min。

答案为56.5。

15.提示：n为18+12+6=36的正约数。因为18∶12∶6=3∶2∶1,所以n为6的倍数。因此n=6,12,18,24,30,36。又因为当样本容量为n+1时,若采用系统抽样法,则需要剔除1个个体,所以n+1为35的正约数,因此n=6。

答案为6。

答案为②③。

三、解答题

(2)由于年利润z=x(8.69-1.23x)-2x=-1.23x2+6.69x,所以当x≈2.72(t)时,年利润z最大。

18.提示：(1)由题意可知,补充完整的茎叶图如图1所示。

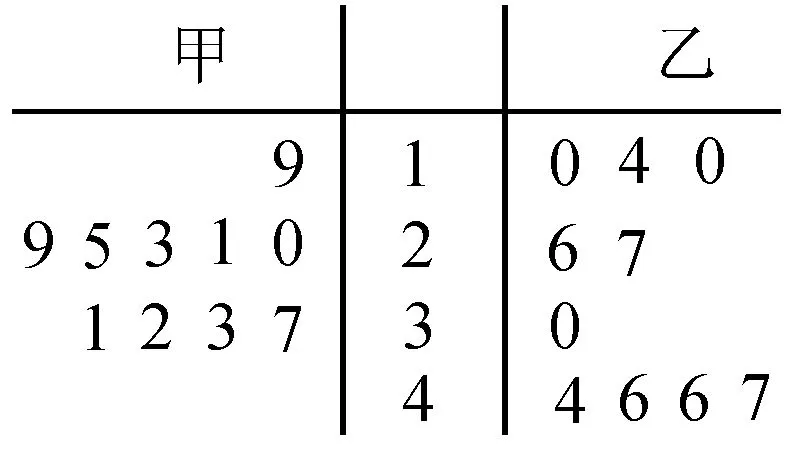
图1

统计结论如下：①甲种树苗的平均高度小于乙种树苗的平均高度。②甲种树苗比乙种树苗长得更整齐。③甲种树苗的中位数为27,乙种树苗的中位数为28.5。④甲种树苗的高度基本上是对称的,且大多数集中在均值附近,乙种树苗的高度分布较为分散。