例析频率分布直方图中的问题

■张 钢 张启兆

频率分布直方图中的相关问题是高考的热点问题,那么,频率分布直方图中到底涉及哪些问题,又如何求解呢?下面举例分析,供同学们学习与提高。

例1(2018年高考全国卷)某家庭记录了未使用节水龙头50天的日用水量数据(单位：m3)和使用了节水龙头50天的日用水量数据,得到了频数分布表分别如表1,2所示。

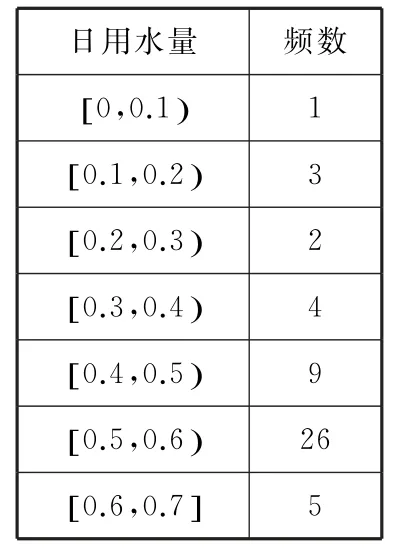
表1

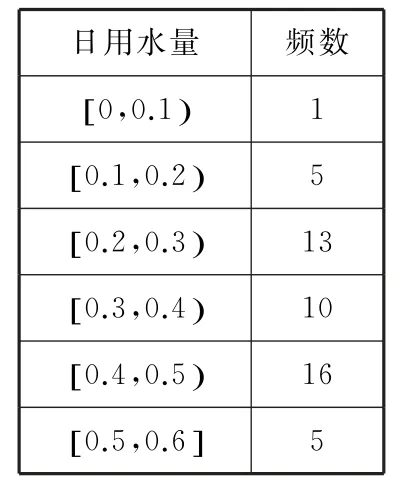
表2

(1)作出使用了节水龙头50天的日用水量数据的频率分布直方图。

(2)估计该家庭使用了节水龙头后,日用水量小于0.35m3的概率。

(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间的中点值作代表)

解：(1)由题意画出频率分布直方图,如图1所示。

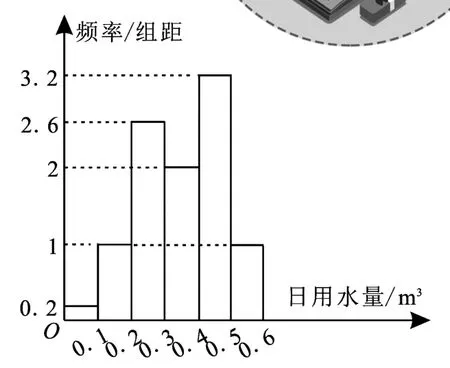
图1

(2)根据以上数据,该家庭使用了节水龙头后50天日用水量小于0.35m3的频率为0.2×0.1+1×0.1+2.6×0.1+2×0.05=0.48,因此该家庭使用了节水龙头后日用水量小于0.35m3的概率的估计值为0.48(频率的近似值可视为概率)。

估计使用节水龙头后,一年可节省水(0.48-0.35)×365=47.45(m3)。

评注：本题主要考查频率分布直方图的绘制,考查利用样本估计总体以及对数据的处理能力。通过本题的解析,可以得到频率分布直方图中所涉及的3个注意点：①在画频率分布直方图时,一定要注意纵轴表示的②求某一范围内的频数或频率(概率),只需将这一范围内的频数或频率相加即可。③众数是最高矩形底边中点横坐标所对应的数据,它表示样本数据的中心值;中位数是一组数据按从小到大(或从大到小)的顺序依次排列,处在中间位置的一个数(或最中间两个数据的平均数),在频率分布直方图中,中位数左边和右边的直方图面积相等,由此可估计中位数的值,但有偏差;样本数据的平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和。

例2某市组织高一全体学生参加计算机操作比赛,比赛成绩等级分为1至10分,随机调阅了A,B两所学校各60名学生的成绩,得到样本数据A校的条形图(如图2)和样本数据B校的统计表(如表3)。

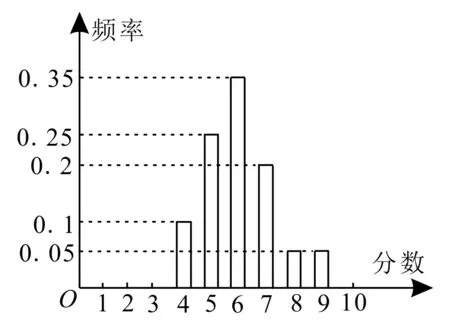
图2

表3

(1)计算两校样本数据的均值和方差,并根据所得数据进行比较。

(2)从A校样本数据成绩分别为7分,8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人,求这2人成绩之和大于或等于15的概率。

解：(1)由A校样本数据的条形图可知,成绩分别为4分,5分,6分,7分,8分,9分的学生分别有6人,15人,21人,12人,3人,3人。

所有基本事件为ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef,共15种情况,其中满足条件的基本事件为ae,af,be,bf,ce,cf,de,df,ef,共9种情况,所以从抽取的6人中任选2人,这2人成绩之和大于或等于15的概率为

评注：本题主要考查平均数、方差的求法。理解频率分布直方图中常用的几个等量关系是解决这类问题的关键,频率分布直方图中常用的7个等量关系：①频率=