一类半正椭圆方程径向正解的存在性
2021-07-15符谦
符 谦
(广西师范大学 数学与统计学院, 广西 桂林 541006)
1 引言及主要结果
考虑下列半正椭圆方程径向正解的存在性与不存在性:

(1)
其中Ω⊂N(N≥2)是一个环A或者单位球B, 参数λ>0,f∈C([0,∞),)且f(0)<0(半正),k: [a,b]→[0,∞)且k(|x|)不恒为0.此外, 当Ω为球时,k为线性映射; 当Ω为环时,k为单调增函数.环A和单位球B分别定义为
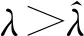
A∶={x∈N:a<|x| 由于f(0)≠0,k(|x|)不恒为0, 故u(x)恒为0一定不是方程(1)的解.本文总假设N≥2, 考虑方程(1)的正径向解, 令r=|x|,u=u(r), 则方程(1)可改写为 (2) 其中: 当Ω为单位球时,a=0,b=1; 当Ω为环时, 0 u(a)=u(b)=0,Ω=A, (3) u′(0)=u(1)=0,Ω=B. (4) 本文总假设: (H1)f∈C([0,∞),)且满足f(0)<0; (H2) 存在S>0, 使得F(S)>0; (H3) 若F(s)>0, 则f(s)>0; (H5)k: [a,b]→[0,∞)且k(|x|)不恒为0; 此外, 当Ω=B时,k为线性映射; 当Ω=A时,k为单调增函数; (H6) 若Ω=B, 则存在常数p,c>0, 使得|f(s)|≤c(sp+1)(当N=2时, 0 此外, 可将条件(H4)减弱为: 条件(H6)表明, 当Ω=B时,f(s)在无穷远处具有次临界增长阶; 条件(H4)强于条件(H7), 条件(H7)强于条件(H8).由条件(H1)和(H2)知,f(s)在(0,∞)上有零点, 记f(s)的第一个(最小的)零点为z, 则有 f(s)<0,s∈[0,z);f(z)=0. (5) 定义 Z∶=sup{s>0:F(t)≤0,t∈[0,s]}. (6) 因此0 F(s)≤0,s∈[0,Z];F(Z)=0; (7) F(s)>0,f(s)>0,s∈(Z,∞). (8) 本文主要结果如下. 定理1假设条件(H1),(H5),(H7)成立, 则当λ>0充分小时, 方程(1)没有非负解. 定义集合: (9) 其中Ω⊂N(N≥2)是一个环A或者单位球B.定义泛函 (10) 其中: 当Ω=B时,a=0,b=1; 当Ω=A时, 0 (11) 其边界条件为: 当Ω=B时,v′(0)=v(1)=0; 当Ω=A时,v(a)=v(b)=0.定义 (12) 如果f∈C1[0,∞), 则线性化算子L(uλ)的所有第一特征值均非负. 下面除非特殊说明, 总假设条件(H1)~(H6)成立.定义范数‖u‖p, 其中1≤p≤∞, (14) 任意地固定λ>0, 由式(14)知, 对∀ε>0, 存在一个常数M1=M1(ε)>0, 使得 |F(s)|≤εs2+M1,s∈. (15) 由引理1知,i(λ)能由式(12)定义且i(λ)>-∞.如果u∈H*(Ω)且满足 则称u是I在H*(Ω)中的极小值点.下面寻找I的极小值点u, 并证明其为方程(2)的正径向解.由于I(0,λ)=0, 因此I的下确界非正.若其下确界为0, 则其极小值点可能是u恒为0, 但其并不是方程(2)的解, 故其下确界是负的. 证明: 首先证明存在一个函数V(x)满足V∈H*(Ω),V(r)不恒为0, 且 (17) 引理3若i(λ)<0, 则当λ′>λ时,i(λ′)<0. 证明: 令i(λ)<0, 则存在一点u∈H*(Ω), 使得I(u,λ)<0, 即 因此 当λ′>λ时, 有 即i(λ′)≤I(u,λ′) 引理4假设条件(H1),(H8)成立, 则存在一个λ1>0, 使得当λ∈(0,λ1)时, 有I(u,λ)≥0(u∈H*(Ω)),i(λ)=0. 证明: 由于f(0)<0, 则对较小的s>0, 存在常数c>0, 使得F(s)≤-cs, 结合条件(H8)知, 存在常数M3=M3(s)>0, 使得F(s)≤M3s2(s≥0), 再结合条件(H5)可得 定义 λ*∶=inf{λ>0:i(λ)<0}. (18) 由引理2~引理4知,λ*>0. 引理5[12]当λ≤λ*时,i(λ)=0; 当λ>λ*时,i(λ)<0. 定理3若λ>λ*, 则I(·,λ) 在H*(Ω)中存在极小值点. 证明: 若λ>λ*, 则由引理5知i(λ)<0.由引理1知,I(·,λ)在H*(Ω)中有下界且其下确界是负的.定义 |F(s)|≤C(s2+1),s∈. 因此F(vn)的积分收敛到F(v0)的积分[21], 即 (19) 结合I(u)的定义和I(vn)→I0及式(19), 知 其中I0是I(u)的下确界.表明 (20) 因为在H*(Ω)中vn⇀v0, 所以 (21) 虽然找到了I(·,λ)在H*(Ω)中的极小值点, 但并不能确定其是否为I(·,λ)的一个临界点.对于极小值点u, 令h(t)∶=I(u+tv,λ), 其中v∈H*(Ω)为任意的试验函数.由于u是一个极小值点, 则对于t≥0, 有h(0)≤h(t), 因此h′(0)≥0.若对于一个较小的ε>0, 有 h(0)≤h(t),t∈(-ε,ε), (22) 则h′(0)=0且u为I的一个临界点. 对于a≤ri-1 (23) (24) 当λ>λ*时, 由引理5知,i(λ)<0.由定理3知,I(·,λ)在H*(Ω)中有极小值点. 引理7若λ*≤λ<∞且u是I(·,λ)在H*(Ω)中的极小值点, 满足u不恒为0, 则有: 1) 存在r∈(a,b), 使得u(r)>Z; 2) 若存在a≤r1≤r2≤b, 使得u(r1)=u(r2)=0,u(r)>0(r∈(r1,r2)), 则存在r3∈(r1,r2), 使得u(r3)>Z. 证明: 当λ>λ*时,I(u,λ)=i(λ)<0, 显然u不恒为0; 而当λ=λ*时,i(λ*)=0, 极小值点可能是u恒为0, 而题设条件排除了这样的极小值点. 1) 用反证法.假设对∀r∈(a,b), 有u(r)≤Z, 则F(u(r))≤0.由于u(r)不恒为0, 因此u′(r)不恒为0.又因为0≤k(r)≤M2, 故I(u,λ)>0.这与I(u,λ)=i(λ)≤0矛盾, 故1)成立. 2) 假设u(r1)=u(r2)=0,u(r)>0(r∈(r1,r2)).用反证法.若对∀r∈(r1,r2),u(r)≤Z, 则F(u(r))≤0, 由于u′(r) 不恒为0, 0≤k(r)≤M2, 故有 定义当r∈[a,b](r1,r2)时,v(r)∶=u(r); 当r∈(r1,r2)时,v(r)∶=0, 则v∈H*(Ω), 且 I(v;r1,r2)=0,I(v;a,r1)=I(u;a,r1),I(v;r2,b)=I(u;r2,b). 由式(24)知, 这与u是I(·,λ)在H*(Ω)中的极小值点矛盾, 故存在r3∈(r1,r2), 使得u(r3)>Z.证毕. 引理8若λ*≤λ<∞且u是I(·,λ)在H*(Ω)中的极小值点, 满足u不恒为0, 则存在一串序列tn∈(a,b), 使得u(tn)>0且tn→b(n→∞).若Ω=A, 则存在一串序列sn∈(a,b), 使得u(sn)>0且sn→a(n→∞). 证明: 令Ω=B, 则a=0,b=1, 证明存在序列tn∈(0,1), 使得u(tn)>0,tn→1(n→∞). 用反证法.假设tn不存在, 则对任意固定的δ∈(0,1), 有u(r)恒为0(r∈[δ,1]).定义v(r)∶=u(δr)(r∈[0,1]), 显然v∈H*(B).利用变量代换s=δr, 并结合条件(H5), 计算 令 则有I(v)=h(δ)且I(u)=h(1)=P-Q.由于I(u)=i(λ)≤0, 因此有P≤Q, 由于u不恒为0, 所以P>0.对于t∈(0,1], 当N=2时,h(t)=P-Qt-3,h′(t)=3Qt-4>0; 当N≥3时, 因此h(t)在(0,1]上递增, 且有I(v)=h(δ) 令Ω=A, 证明存在序列tn∈(a,b), 使得u(tn)>0且tn→b(n→∞).用反证法.假设对任意固定的δ∈(0,1), 有u(r)恒为0(r∈[δb,b]).延拓u(r), 令u(r)恒为0(r∈[a,b]).定义v(r)∶=u(δr)(r∈[a,b]), 则v(a)=v(b)=0且v∈H*(A).余下证明与Ω=B情形相同, 故略.从而存在序列tn∈(a,b), 使得u(tn)>0且tn→b(n→∞). 当Ω=A时, 证明存在序列sn∈(a,b), 使得u(sn)>0且sn→a(n→∞).用反证法.假设对某个r0>a, 有u(r)恒为0(r∈[a,r0]), 由引理7中1)知, 存在一个点r1, 使得r0 v(r)∶=u(r-a+r0)(r∈[a,a1]),v(r)∶=Z(r∈[a1,r1]),v(r)∶=u(r)(r∈[r1,b]), 则v∈H*(A).利用变量代换t=r-a+r0, 有 由于当t∈[r0,r1]时,F(u(t))≤0且F(u(t))不恒为0,u′(t)不恒为0, 0≤k(t)≤M2, 因此被积函数是正的.又因为k(r)单调递增, 所以 由于I(v;a1,r1)=0,I(u;a,r0)=0,I(v;r1,b)=I(u;r1,b), 因此有 矛盾, 故存在一串序列sn∈(a,b), 使得u(sn)>0且sn→a(n→∞).证毕. 引理9[12]令λ*≤λ<∞且u是I(·,λ)在H*(Ω)中的极小值点, 满足u不恒为0.则当Ω=B时,u(r)>0(r∈(0,1)); 当Ω=A时,u(r)>0(r∈(a,b)). 若Ω⊂N(N≥2)是一个环或单位球, 则由f(0)<0及条件(H7)知, 存在M4=M4(s)>0, 使得f(s)≤M4s(s≥0).由条件(H5)知, 存在M2=M2(Ω)>0, 使得0≤k(|x|)≤M2.用反证法.假设当λ>0充分小时,u是方程(1)的一个非负解.令μ1是-Δ带有Dirichlet边界条件的第一特征值, 且φ是其对应的特征函数, 满足φ(x)>0, 则有 -Δu=λk(|x|)f(u)≤λM2M4u, (25) 将式(25)两边与φ做L2内积, 得 μ1(u,φ)L2≤λM2M4(u,φ)L2, 定理4令λ>λ*且uλ是I(·,λ)在H*(Ω)中的极小值点, 则其为方程(2)的一个正解, 且属于C2[a,b]并满足I(uλ,λ)=i(λ)<0. 故u是方程(2)的一个弱解.当Ω=B时, 由椭圆正则性理论及假设条件(H6), 可得u∈W2,q(Ω)(∀q∈[1,∞)); 当Ω=A时, 由引理6知,u∈C1/2[a,b], 结合椭圆正则性理论可知,u∈W2,q(Ω)(∀q∈[1,∞)).此外, 由于方程(2)是一个常微分方程, 且f(u(r))∈C[a,b], 则u∈C2[a,b].证毕. 定理5对于λ=λ*, 方程(2)有一个正解u*(u*∈C2[a,b]), 且满足I(u*,λ*)=i(λ*)=0. 证明: 令λn是一串序列,λn>λ*且λn→λ*(n→∞).设un是由定理4得到的相应λ=λn的极小值点.由于I(un,λn)<0, 因此 结合式(15)及0≤k(r)≤M2, 有 当n→∞, 有 因此,u*是方程(2)的弱解, 再结合定理4的证明过程, 可得u*∈C2[a,b].由于un是相应λ=λn的极小值点, 因此有I(un,λn)≤I(v,λn)(v∈H*(Ω)).当n→∞时, 有I(u*,λ*)≤I(v,λ*), 因此u*是I(·,λ*)的极小值点, 即I(u*,λ*)=i(λ*)=0.由于u*是方程(2)的解且u*不恒为0, 再结合引理9和引理10知,u*在Ω中严格正.证毕. 若f∈C1[0,∞), 下面证明线性化算子L(uλ)的所有第一特征值均非负.固定λ∈[λ*,∞), 令u=uλ, 则二阶导数I″(u)具有双线性形式
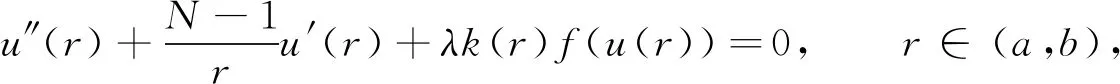

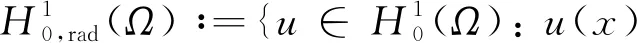




2 极小值点的存在性
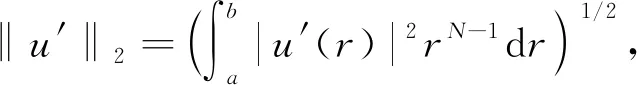

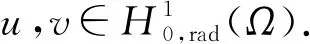



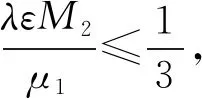



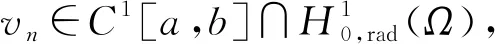






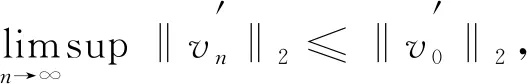
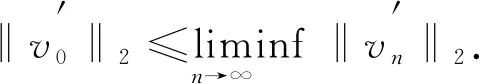
3 极小值点的性质
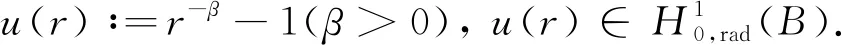
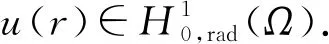


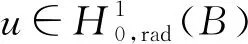
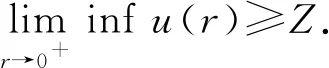
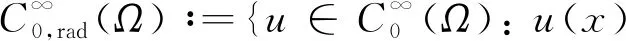
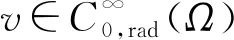
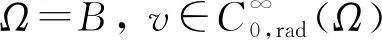
4 主要结果的证明
4.1 定理1的证明

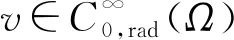

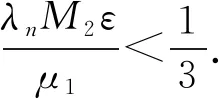
4.2 定理2的证明




