多层阵列式光电坐标靶测量方法研究*
2019-12-30史元元张文博杨曼曼
史元元,冯 斌,张文博,胥 磊,杨曼曼
(西安工业大学 光电工程学院, 西安 710021)
在外弹道测试领域,射击密集度表征了弹着点对散布中心的离散程度,是武器系统测试中的一个重要参数,直接关系到武器弹药在其有效射击范围内的打击精度[1],而射击密集度是在已知弹丸着靶坐标的基础上,根据散布误差公式计算得到,因此精确地获取弹丸的着靶坐标至关重要[2-3]。早期射击密集度的测量一般采用接触式测量方法,用木板、纸板及纱网等材料在弹道终点竖立一个垂直的靶面,射击过后采用人工方法对弹丸的坐标进行测量,然后进行射击密集度的计算。该测量方法耗费大量人力、物力及财力,而且受到人为因素的影响比较大,严重影响弹着点坐标的测量精度[4]。
随着科学技术的发展,国内外学者提出了非接触式弹着点坐标测量方法,测试完成后实时得到弹丸数据。目前,靶场测试中所用的设备主要有声靶、线阵CCD立靶、四光幕精度靶、四光幕天幕立靶、六光幕精度靶及六光幕天幕立靶等。在进行精度测试时,利用这些测试设备对每发弹丸的着靶坐标进行测量,然后根据散布误差算法得到射击精度[5]。文献[6]提出了一种基于半导体激光平行光管和光电二极管接收阵列的光栅式立靶测量方案。该方案解决了因激光器外部尺寸大于光斑尺寸造成的光幕盲区问题,从理论上分析了系统存在的误差并进行了实弹对比实验,但在构建平行光幕时光路难调节,测量精度较低。文献[7]提出了一种基于线激光平行检测阵列组合的测试方法,用于弹着点坐标的测量。该方法在构建测量光幕时结构简单,便于调节,但测量精度较低。文献[8]介绍了一种编码式光幕立靶测量系统,通过解码电路和弹丸位置算法得到弹丸的着靶坐标。该系统克服了光纤编码的复杂性,电路设计简单,但为了确保采集数据的可靠性,需引入信号采集技术,成本较高,实时性较低。文献[9]提出了一种单靶面非接触式弹着点坐标的测量框架,通过对传统测量框架的优化设计,光源发出的光线通过测量框架形成组合光幕实现对弹着点坐标的测量。该框架结构简单,易于调节,但文中只对整个测量过程进行了理论分析,未涉及具体的算法和精度分析。针对现有弹着点测量方法中存在的不足,本文提出了一种用于测量弹着点坐标的多层阵列式光电坐标靶。通过对多层阵列式光电坐标靶结构、测量原理以及测量误差进行分析,以期解决传统组合光幕存在的光路难调节,测量精度较低及成本高等问题,为后续高精度光电坐标靶的研究奠定了理论基础。
1 光电坐标靶结构设计
1.1 典型的光幕结构
本文所述的多层阵列式光电坐标靶属于光幕立靶的一种。对于光幕立靶,国内目前采用的典型的光幕组合结构有两种,如图1所示。图1(a)采用发光器件和光电接收器件以点对点的方式组成光幕,弹丸坐标计算简单,但是当构建大靶面时,所需发光器件和接收器件的数量较多,且点对点光路难以调节,导致测量精度较低[10-13]。图1(b)将透镜和发光器件组合成光学系统,使得光线通过光学系统后形成平行光幕,但光学系统搭建较困难,平行光幕的无缝拼接难以实现,不易构建大靶面[14-16]。
1.2 多层阵列式光电坐标靶的光幕结构
为了解决典型光幕结构存在的光路难调节问题,提出了一种用于测量弹着点坐标的多层阵列式光电坐标靶,其光幕结构示意图如图2所示。图2中黑线相交的区域为有效测试靶面。发光二极管的发光视场为三角形,在进行光幕组合时为了形成矩形光幕,设计了1号和2号两种类型的测量框架。整个靶体结构包括一个靶架,两个1号测量框架及两个2号测量框架。1号测量框架分布在靶框的顶部和右侧,2号测量框架分布在靶框的底部和左侧。测量框架均包括最底层光阑板、中间层光阑板及最顶层光阑板,每层光阑板上均分布有一定数量的发光器孔和接收器孔阵列。接收器孔阵列中接收器孔的分布示意图如图3所示。
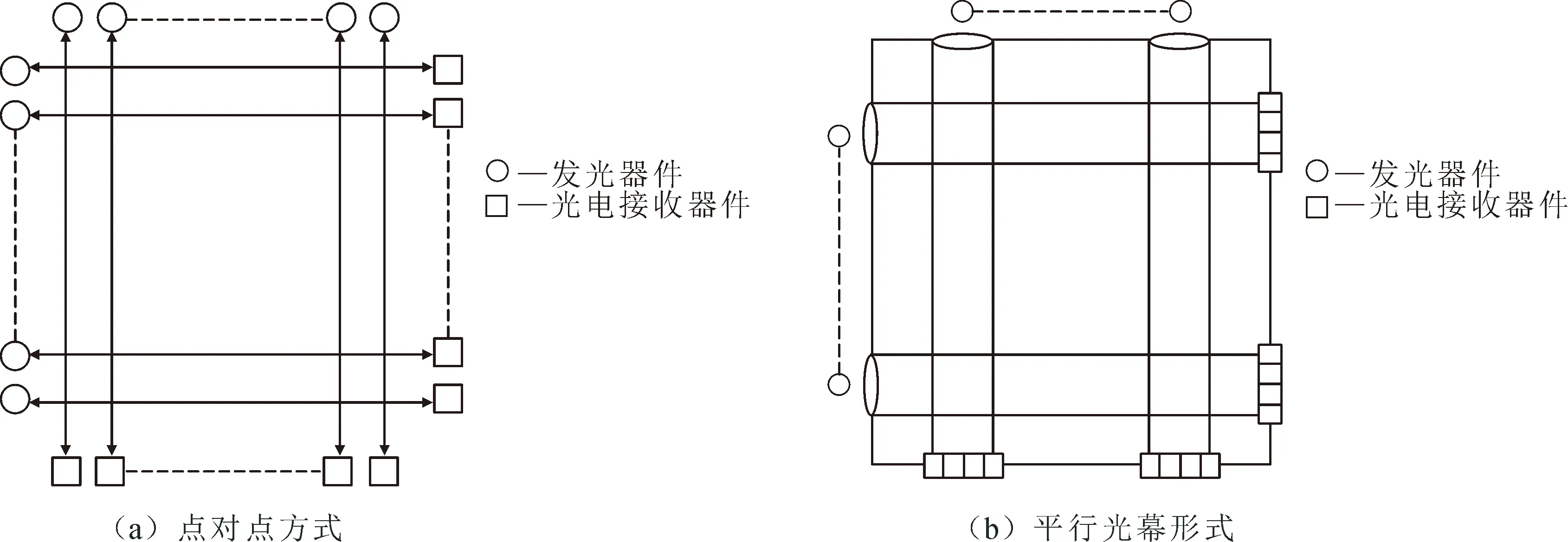
图1 典型光电立靶光幕结构
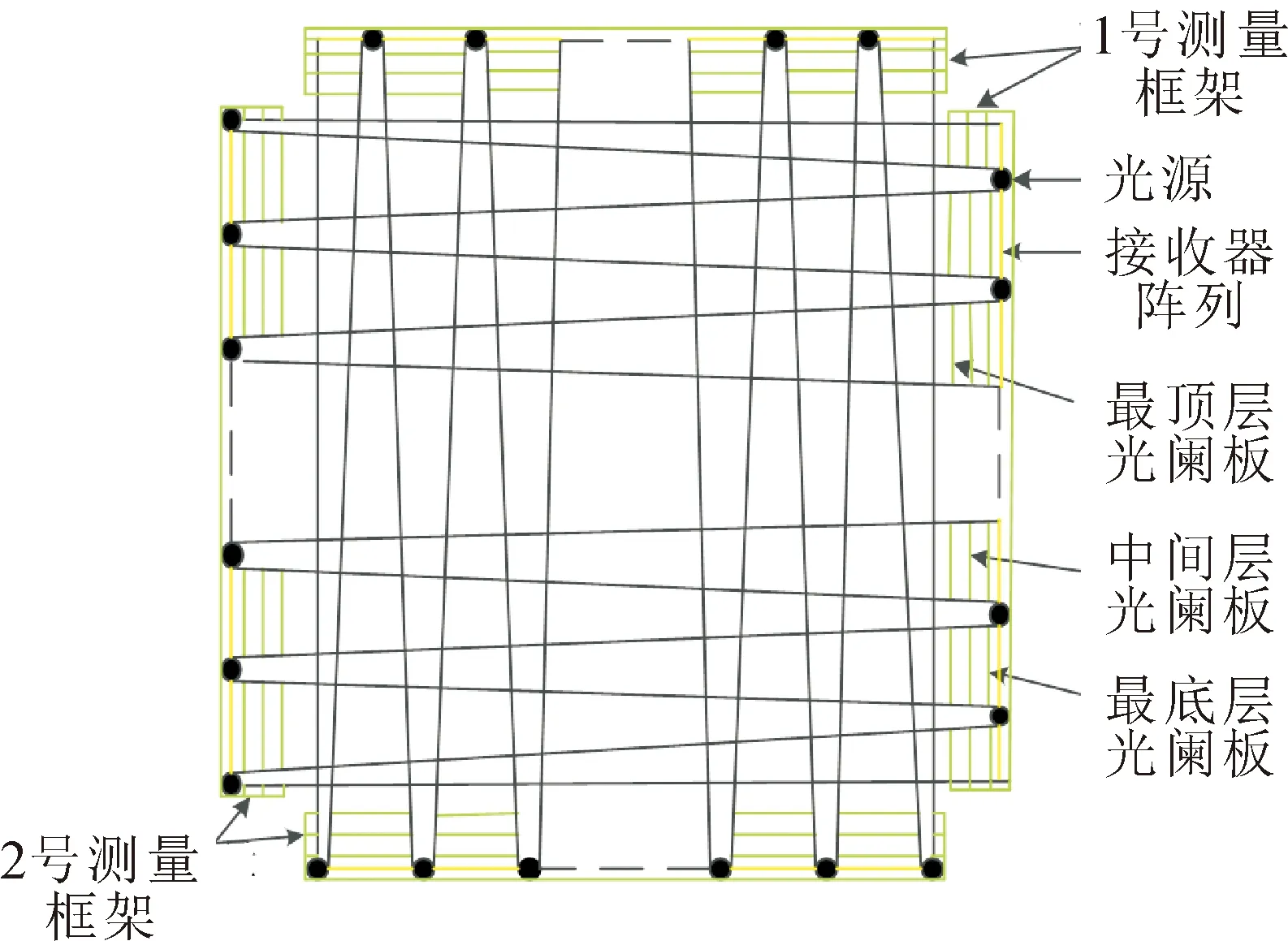
图2 光幕结构示意图
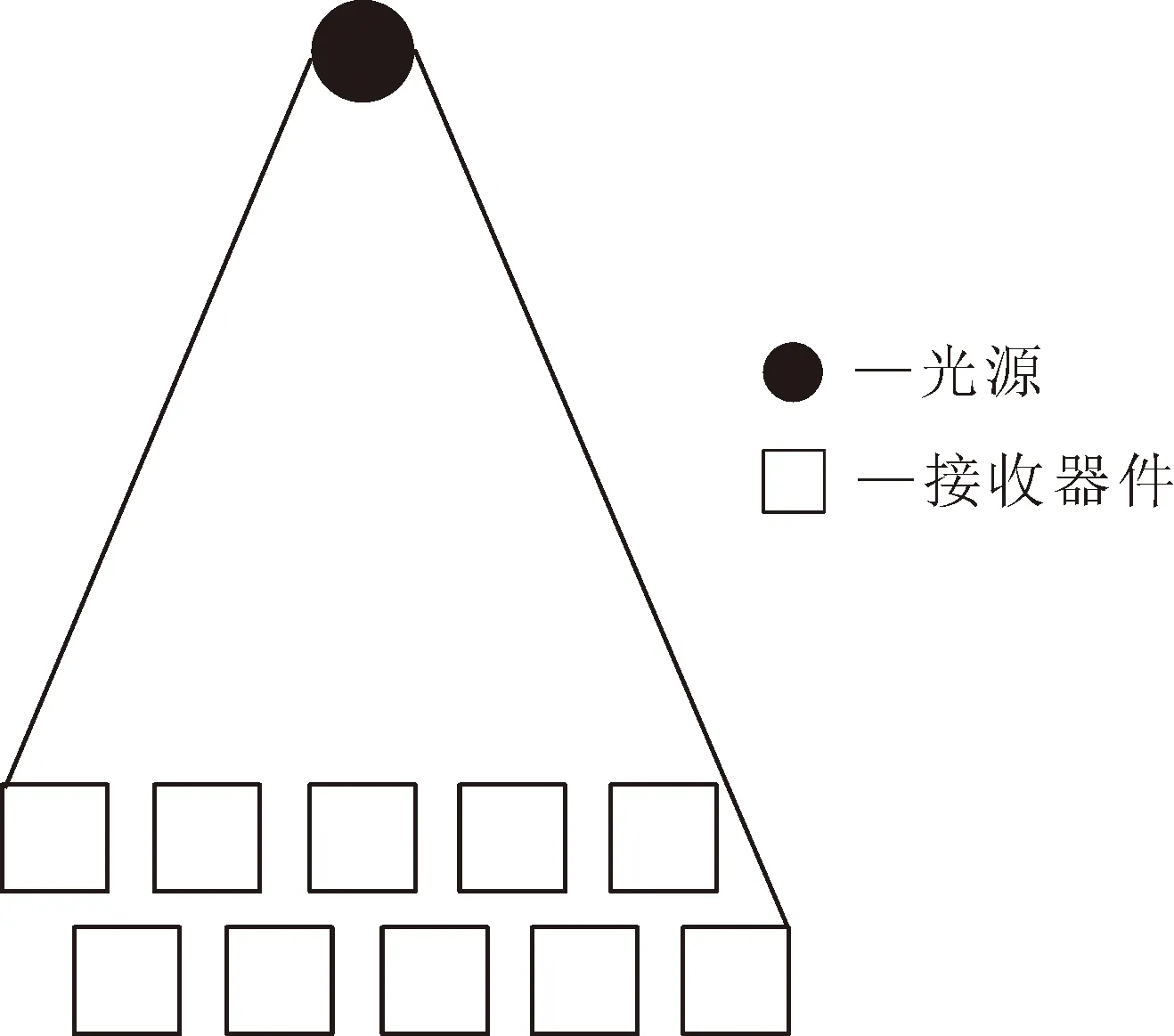
图3 接收器孔排列方式示意图
1.3 多层光阑板作用原理
根据发光二极管的视场范围、光幕尺寸及接收器件的尺寸等参数,可以在理论计算的基础上完成对多层光阑的参数设计。每层光阑板上均分布有发光器孔和接收器孔(如图2所示),为避免每层光阑板上的发射光线和接收光线相互干扰,在发光器孔和接收器阵列之间安装一个分隔板,分隔板的位置分布图如图4所示。
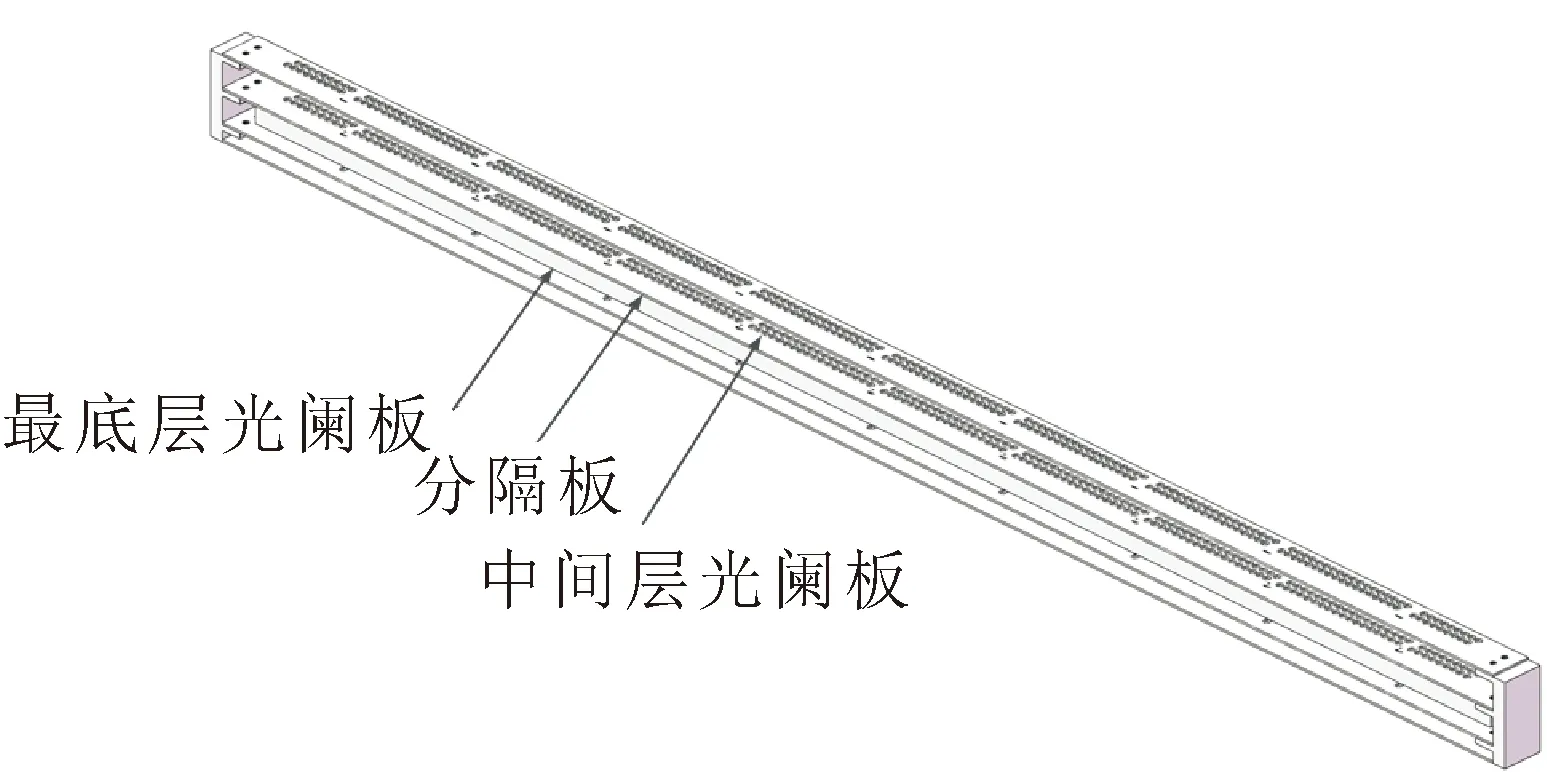
图4 分隔板位置示意图
1号测量框架的结构立体图如图5(a)所示,其局部放大图如图5(b)所示。单个光源的发光视场仿真图如图6所示。光线通过多层光阑板上发光器孔的示意图如图7所示。
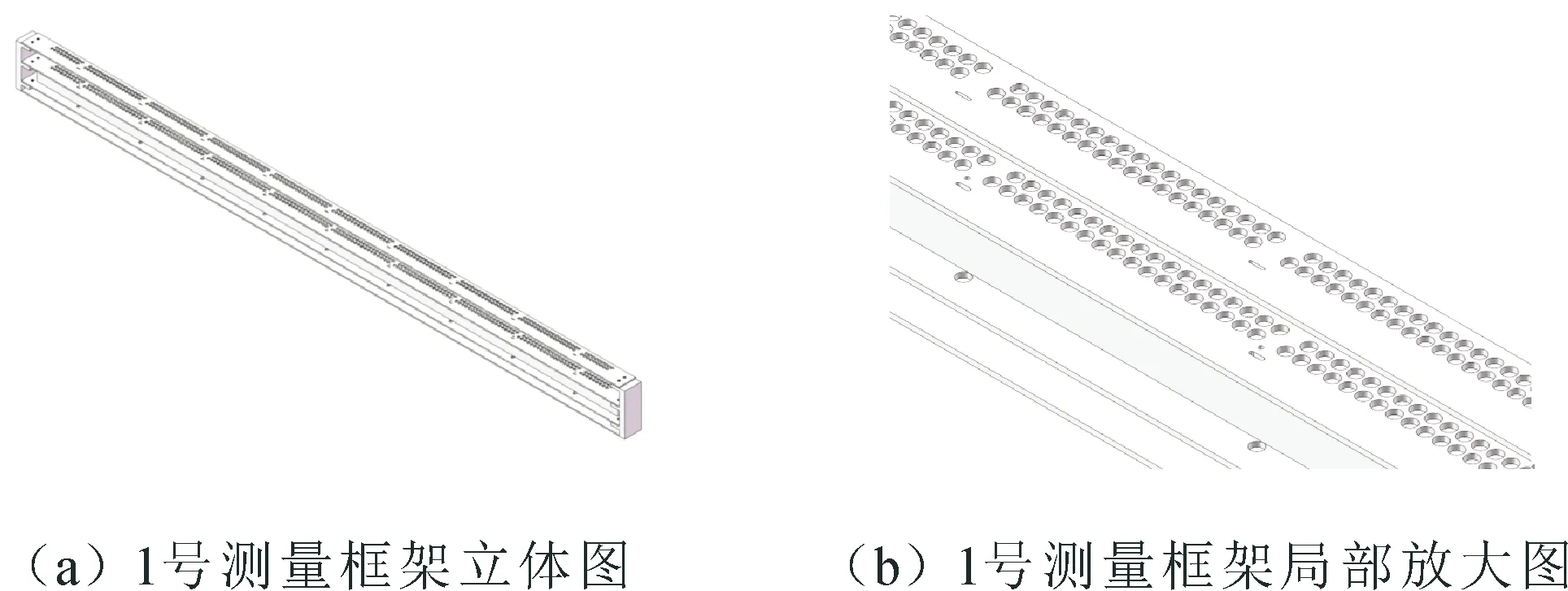
图5 1号框架整体结构图
从图2、图5和图7中可知,光源和接收器件安装在最底层光阑板的正下方,最底层光阑板上发光器孔和接收器孔的形状尺寸与光源和光电器件相同,其作用是使光源光线和到达光电器件的光线得到高效利用。中间层光阑板上的发光器孔则是根据光源发光立体角设计的矩形狭缝,用来限制发光二极管的照射范围,其尺寸在长度上比最底层略大;接收器孔的尺寸与最底层相同,形状呈圆形不同于最底层的矩形接收器孔。最顶层的发光器孔比中间层略大,以形成发散的光幕;接收器孔形状和尺寸与中间层相同。

图6 单个光源视场图Fig.6 Field of view of single light source
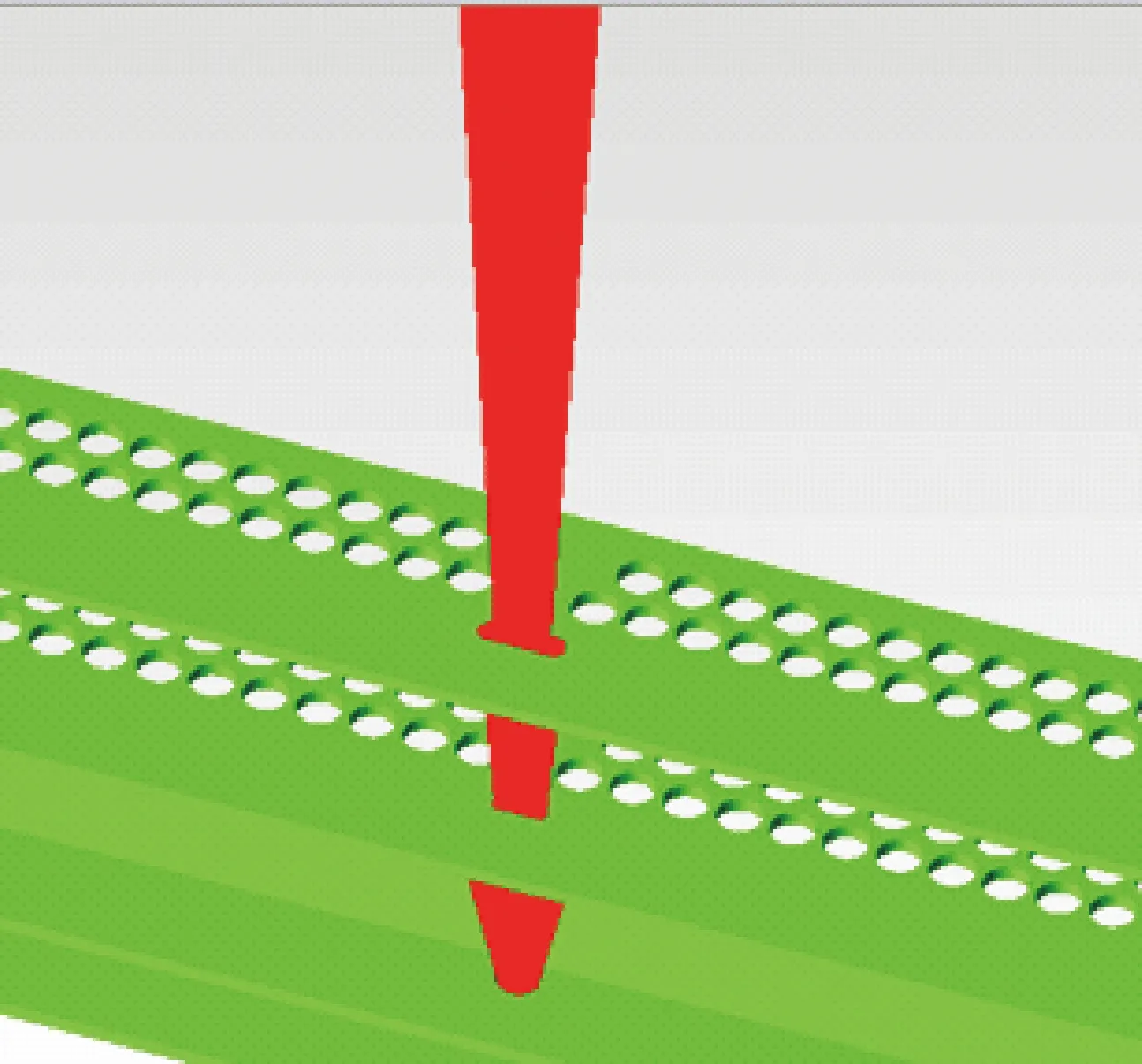
图7 发光器孔作用示意图
根据图6和图7,从多层光阑板的结构分析,当光源光线通过发光器孔照射到其对应的最顶层光阑板上时,呈矩形面。采用一个接收器孔阵列对光线进行接收,接收器孔阵列中包含一定数量的孔,这些孔将整个光源的照射面分割成若干条光束,每一条光束对应一个接收器件,从而实现了对光幕的细分。
2 多层阵列式光电坐标靶测量原理
弹丸穿过靶面时在X轴和Y轴方向上遮挡了一部分到达光电二极管的光,弹丸坐标的计算图如图8所示。通过检测电路的输出信号可以识别出光信号变化的光电二极管位置,根据光源和光信号变化光电二极管的位置即可计算出弹着点坐标。
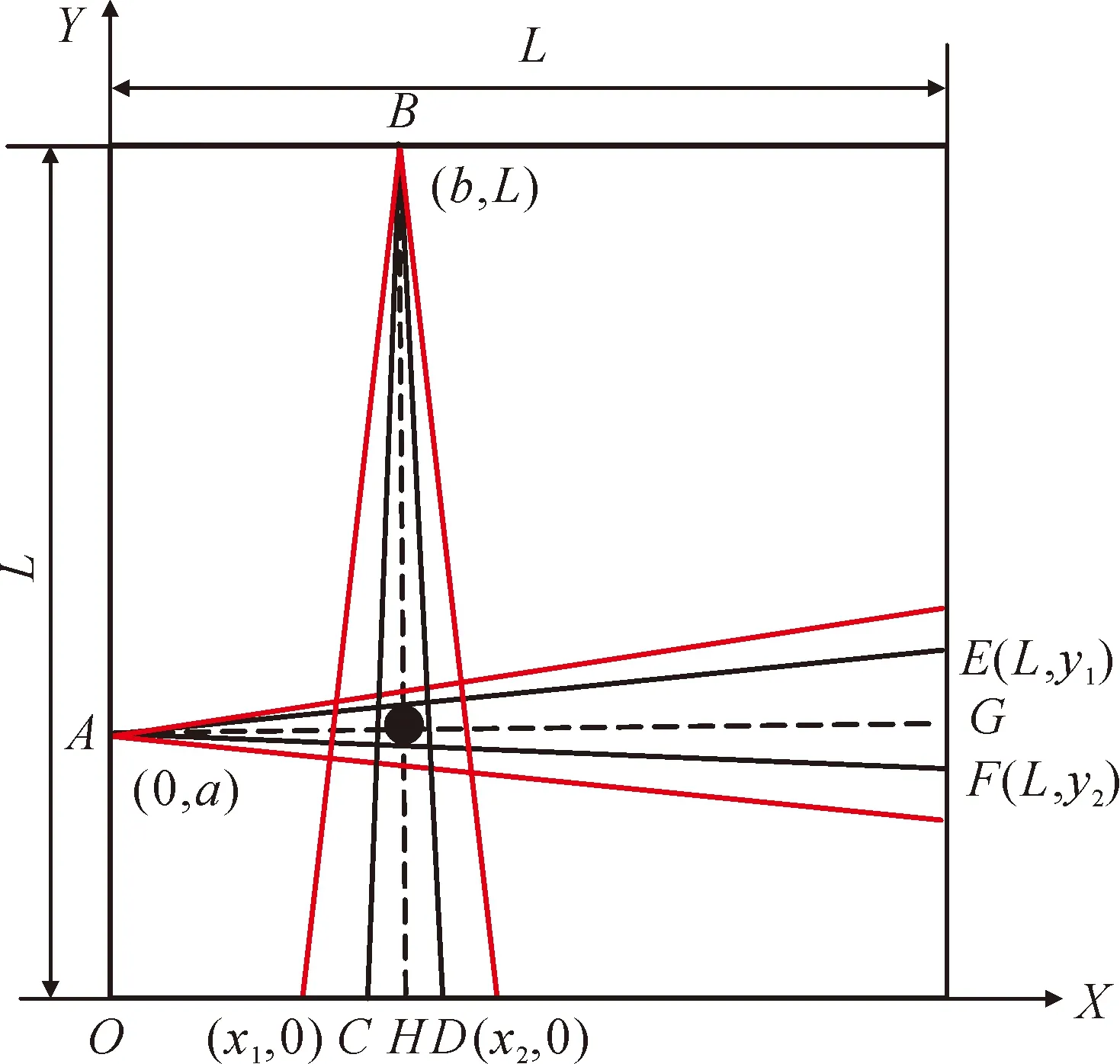
图8 弹丸坐标计算图
以靶面左下角为原点建立坐标系O-XY。红色部分为光幕区域,图8中CD的距离即为弹丸在X轴方向上遮挡住光电二极管的范围(x1~x2),EF的距离即为弹丸在Y轴方向上的遮挡区域(y1~y2),A和B两点为光源的位置,根据检测电路的输出信号则可得到图8中6个点(A,B,C,D,E,F)的坐标。以弹丸的中心在靶面上的坐标为弹着点坐标,通过求直线BH和AG交点的方式确定弹丸中心坐标,而直线BH和AG分别是图8中∠CBD和∠EAF的角平分线。现设H点的坐标为(XH,0),G点的坐标为(L,YG),则BH和AG的直线方程分别为
(1)
由式(1)可得到弹丸的坐标(x,y) ,其中XH和YG未知。弹丸坐标计算的辅助图如图9所示。

图9 弹丸坐标计算辅助图
根据图9中的几何和三角关系可得到XH和YG。
令∠CBD=θ,∠CBM=β,过B点作BM⊥CD,过C点作CP⊥BO1,则有:
(2)
已知:BO1=MO=b,则:
(3)
则H点的横坐标XH为
(4)
式中:θ=β+arctan(x2-b)/L;β=arctan(b-x1)/L。
同理,通过对ΔAEF做辅助线可以得到:
(5)
式中:δ=γ+arctan(y1-a)/L;γ=arctan(a-y2)/L
结合式(1)可以得到弹丸坐标的表达式为
(6)
3 误差分析
3.1 XH输出误差分析
弹丸投影示意图如图10所示。由图10可知,弹丸穿过光幕时,遮住的光电二极管的长度大于其自身尺寸,在不考虑其他因素的条件下,通过对弹丸飞过靶面遮住光电二极管的情况进行分析,进而得到弹丸位置检测精度。

图10 弹丸投影示意图
现假设弹丸在接收器孔阵列上的投影长度为S,光电二极管的间隔距离为d。假定弹丸遮住光电二极管感光面的50%时,才能输出有效信号,那么弹丸可以遮住的光电二极管的数量会出现S/d或(S/d)+1这两种情况。
若弹丸遮住光电二极管的数量为S/d时,即投影长度S能够整除光电二极管的间隔距离d,则检测到光电二极管的位置精度为
Δ=d/2
(7)
当弹丸遮住光电二极管的数量为(S/d)+1时,则投影长度不能够整除光电二极管的间隔距离d,即整除后剩余的长度未达到或超过光电二极管感光面的一半,设其整除后的小数部分为r,则检测到光电二极管的位置精度为
Δ=d/2+(d*r)/2
(8)
对式(7)和式(8)进行整合,得到光电二极管的位置精度为
Δ=(d+S-[S/d]*d)/2
(9)
其中[S/d]为弹丸投影长度被光电二极管中心距整除的倍数。
根据弹丸穿过靶面的位置不同,其S-[S/d]*d的取值范围为[0,d),因此,在不考虑其他因素的条件下,Δ的取值范围为
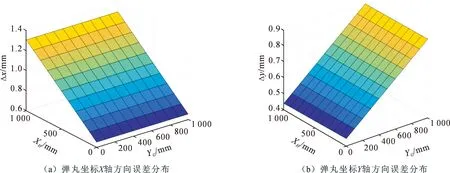
d/2≤Δ (10) 对式(4)两边求偏导,可得: (11) 式(11)可以写成: (12) 根据图8,靶面的大小L远大于b-x1和b-x2,则可得XH的检测精度为 (13) 结合式(10),则XH的检测精度范围为d/2≤ΔXH 同理,YG的检测精度范围为d/2≤ΔYG 靶面四周均分布有光源,对每个光源对应的接收器阵列进行编号,即光源和接收器阵列式一一对应。当利用信号采集电路对接收阵列的输出信号进行采集时,即可得到弹丸遮住光电二极管的位置x1,x2和y1,y2的值,根据接收阵列输出信号的位置可以进一步得到光源的位置。由于靶面的尺寸已知,则可根据式(4)和式(5)得到H和G两点的表达式,最后根据光源的位置和靶面尺寸及XH,YG的表达式按照式(6)计算出弹丸的坐标。 式(6)中a,b点为光源的位置,其可根据多层光阑结构参数进行标定,即光源的位置已知。靶面的尺寸为1 m×1 m,则L为1 000 mm,则式(6)只含XH和YG两个变量,即在靶面内影响弹丸坐标误差的是XH和YG的检测精度。为了对所建立弹着点数理模型进行分析,对式(6)求偏导得: (14) 式中:A1=L2+(b-XH)(a-YG),B1=(ab+LXH-aXH)。 光电器件尺寸选用3 mm,根据图3的排列方式,两个光电二极管之间留出1 mm的安装位置,则相邻两个接收器孔的间隔距离d=2 mm,可得XH和YG的检测精度范围为[1,2)。利用Matlab进行误差仿真分析。可得到整个靶面内弹丸X和Y轴误差的分布图如图11所示。 由图11可知,弹丸坐标X轴误差最大不超过1.3 mm,Y轴误差最大不超过0.9 mm,在同等条件下,当光电二极管紧密排列时(d=4 mm),则XH和YG的检测精度范围为[2,4),弹丸坐标的测量误差分布如图12所示。由图12可知,弹丸坐标X轴误差最大不超过2.6 mm,Y轴误差最大不超过1.8 mm。对比两个结果可知,光电二极管之间的间距越小,坐标计算误差越小。因此,本文采用两排光电二极管对光线进行接收的方法减小了光电二极管之间的距离,能有效提高测量精度。 图11 d=2 mm时弹丸坐标误差分布 图12 d=4 mm时弹丸坐标误差分布 本文提出了一种用于测量弹着点坐标的多层阵列式光电坐标靶。利用Solidworks建立了多层阵列式光电坐标靶的整体结构,并对其内部三层光阑板进行了原理性分析,得出结论为 1) 通过Tracepro对光源发出的光线进行了仿真,进一步证明了多层阵列式光电坐标靶结构的可行性。光线通过多层光阑板能在空间形成测量光幕实现对弹丸着靶坐标的测量,而且该结构能够克服传统光幕在构成方式上存在的光路难调节、精度低等问题。 2) 分析了有效靶面为1 m×1 m,光电二极管尺寸为3 mm时,弹着点坐标的测量误差,其X轴误差最大不超过1.3 mm,Y轴误差最大不超过0.9 mm。在1 m×1 m的靶面内相对误差不超过0.13%,测量精度比较高。 3) 光电二极管的排列方式会影响到弹着点坐标的测量精度,通过对文中光电二极管的排列方式和光电二极管紧密排列时的误差对比可知,光电二极管的间隔越小,测量精度越高,证明了本文所提出的测量方法能实现对弹着点坐标的高精度测量。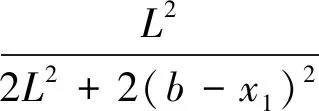

3.2 坐标计算误差分析

4 结 论
