非标齿轮弯曲疲劳试验方案设计
2019-12-30朱燃燃晋民杰元艳玲
朱燃燃,晋民杰,范 英,元艳玲
(太原科技大学 交通与物流学院,山西 太原 030024)
0 引言
齿轮在传动过程中主要失效形式是轮齿折断、齿面磨损、齿面点蚀、齿面胶合等,而因弯曲应力造成的失效形式多为轮齿折断[1]。针对齿轮弯曲疲劳试验及弯曲寿命,国内外专家做了大量工作:北京科技大学的谈嘉祯、王晓群、陶晋等人,从20世纪90年代开始先后对35SiMn调质齿轮、35Cr2MoV调质齿轮、25Cr2MoV离子渗氮齿轮、20CrMnMoA渗碳淬火齿轮、37SiMn2MoV调质齿轮、40MnB调质齿轮、42 SiMn调质齿轮等齿轮的弯曲疲劳强度进行试验,拟合出多种齿轮材料的S-N曲线,为齿轮的疲劳寿命留下了大量的数据[2-3];张涛、王克胜等人根据实测载荷谱,应用Miner法则进行齿轮寿命的预测,在理论、实践和经济上具有重要意义;袁菲等考虑齿轮啮合过程中齿间载荷分布的影响,运用三维有限元分析方法,探究了齿间载荷分布对齿轮弯曲疲劳寿命预测的影响,研究结果表明,考虑齿间载荷分布会降低齿轮的弯曲疲劳寿命。综上所述,在齿轮疲劳试验及寿命研究方面,部分学者从裂纹萌生和扩展入手,用解析法与有限元法相结合的方法进行研究;部分学者主要采用试验方法分析S-N曲线,进而对齿轮进行疲劳寿命分析。
笔者根据标准的齿轮弯曲疲劳强度试验方法,制定齿高系数、顶隙系数等齿形参数为非标准值时的试验方案,用ANSYS验证载荷级别的有效性,为后续研究提供依据。同时,结合试验方案及齿轮材料的性能参数,确定试验齿轮弯曲疲劳特性曲线及疲劳极限应力,采用局部应力应变法分析方法,研究齿高系数对齿轮弯曲疲劳寿命的影响。
1 试验方案确定
按照《GB/T 14230-1993齿轮弯曲疲劳强度试验方法》,根据不同的试验目的,按照不同的试验点组合测定试验齿轮疲劳特性曲线及弯曲疲劳极限应力,本文采用常规试验方法,试验时取5个应力级,每个应力级取5个试验点。
1.1 试验样件确定
为了体现不同齿高系数、顶隙系数及变位系数对齿轮弯曲疲劳强度的影响,现取齿高系数分别为1,1.15,1.25,顶隙系数为0.4(不变位齿轮的三类齿轮)。其他参数的选取均满足标准值:齿数z=30,模数m=5,压力角20°,齿宽14 mm。
1.2 试验载荷级别确定
本研究的齿轮材料是综合性能较好的17CrNiMo6。根据试验齿轮静强度值及齿轮疲劳极限值,计算出MQ试验齿轮的应力级别如表1所示。

表1 MQ试验齿轮应力级别Table 1 MQ test gear stress levels
脉动疲劳试验中,可根据GB/T 14230-1993中的方法来计算齿根处名义弯曲应力,其计算为:

(1)
式中:
Ft——分度圆上圆周力;
YFE——载荷作用于E点时齿轮的齿形系数;
YSE——载荷作用于E点时齿轮的应力修正系数;
YST——试验齿轮的应力修正系数;
YδrelT——相对齿根圆角敏感系数;
YRrelT——相对齿根表面状况系数;
YX——弯曲强度计算的尺度系数。
计算不同齿高系数齿轮齿根应力的各参数如表2所示。

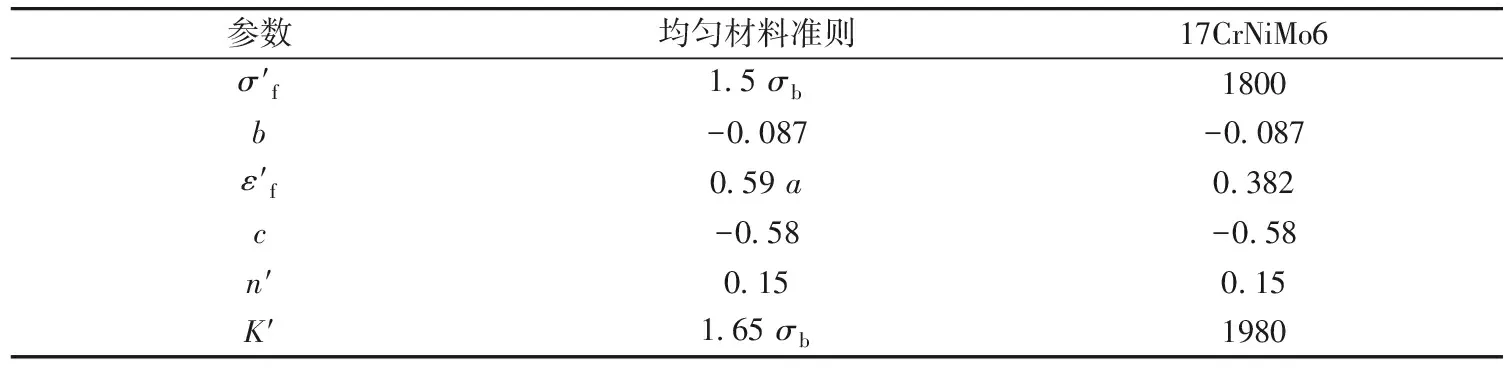
表2 非标齿轮齿根应力参数Table 2 Non-standard gear root stress parameters

图1 齿轮齿高系数-最大齿根弯曲应力值关系曲线Fig.1 Gear tooth height coefficient-maximum root bending stress curve
由图1所描述的齿轮齿高系数与最大齿根弯曲应力值关系,计算出3种不同齿高系数齿轮的5个载荷级别(双齿加载)如表3所示。

表3 MQ质量要求的3种齿高系数齿轮载荷级别Table 3 MQ quality requirements of three high coefficient gear load levels
1.3 加载点位置确定
当齿轮的基本参数发生变化时,试验过程中首次体现在跨齿数的变化和加载点位置的变化。对于双齿加载形式,齿轮几何参数一定,跨齿数n和加载点位置E都是确定的。
E点所在圆的直径:
dE=db/cosαe
(2)
tanαe=π(Z-2n-1)/2Z+2xtanα/Z+invα
(3)
n≈Z[π-2tanαa-0.5(π-4xtanα)+2invα]/2π+0.5
(4)
式中:
db——基圆直径,mm;
n——为跨齿数,四舍五入;
Octet®RED 96 System生物分子相互作用仪,紫外可见分光光度仪,旋转蒸发仪,冷冻离心机,台式冷冻离心机,台式真空泵,磁力搅拌器。
αa——齿顶压力角。
加载示意图如图2所示。
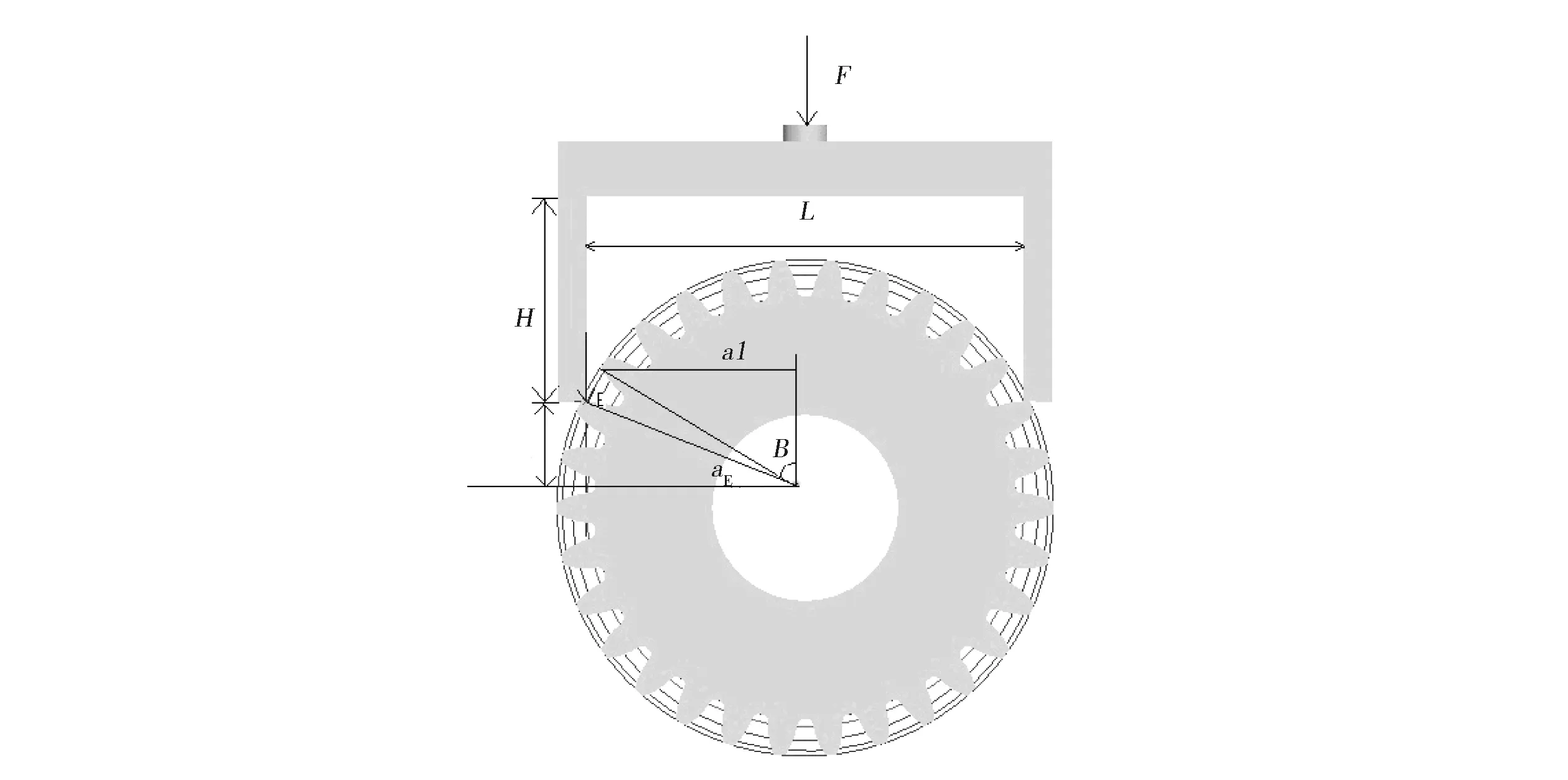
图2 齿轮弯曲疲劳试验双齿加载示意图Fig.2 Schematic diagram of double-tooth loading in gear bending fatigue test
根据上述公式及试验齿轮的基本参数计算得知,齿高系数的变化并未引起加载点位置参数的变化,跨齿数为10,加载点压力角为25.93°,加载点半径为78.36 mm。
在试验过程中为了防止压头的攒动,齿轮试验压头实际上压在水平的两个点上,并与齿轮基圆相切。用Matlab做试验,齿轮所压轮齿的渐开线方程图像,寻找渐开线最高点,并通过做基圆切线与渐开线方程的交点来检验此方法的正确性。结果表明,当齿轮跨齿数为10,ha=1,1.15,1.25时,加载点半径均为78.36 mm,与通过GB/T 14230—1993公式所算结果一致。因此,可得到齿高系数变化时加载点不变化的结论。
E点位置确定之后,L则可按下列关系计算:2a1 a1=rasinβ (5) (6) (7) αa=arccos(rb/ra) (8) (9) 式中: Sa试验齿轮齿顶圆齿厚; S为分度圆弧齿厚; ra为齿顶圆半径; rb为基圆半径; rf为分度圆半径; αa为齿顶压力角。 在非标齿轮弯曲疲劳试验的基础上,估算齿轮的弯曲疲劳寿命,由于弯曲疲劳寿命主要集中在0.5×105~3×106之间,因此用局部应力应变法来进行预估[4-5]。局部应变分析法估算零件寿命步骤如图3所示。 图3 局部应变分析法估算零件寿命步骤框图Fig.3 Part life estimation by local strain analysis 齿轮的材料及其性能参数如表4所示。 表4 齿轮材料特性Table 4 Gear material characteristics 材料的循环应力-应变曲线的表达式为: (10) 式中: σ为应力幅; n′为循环应变硬化指数; 迟滞回线的方程可以表示为: (11) 式中,K′是循环强度系数。 (12) 曼森提出,在局部应力应变分析法中,所使用的应变-寿命曲线表达式为: (13) 式中: N为疲劳寿命,2N为以反复次数计的疲劳寿命; b为疲劳强度指数; c为疲劳延性指数。 式(13)是在低周疲劳的应变-寿命关系式中增加弹性项得出来的。当有平均应力时,式(13)变为: (14) 利用Seeger法从抗拉强度和弹性模量估算材料循环特性,试验齿轮循环特性如表5所示。表中a为延伸率,当σb/E≤0.003时,a=1.0;当σb/E>0.003时,a=1.375-125σb/E。 表5 齿轮材料循环特性Table 5 Material cycle characteristics of gear 根据表5提供的材料的循环特性,可做出材料的应变—寿命曲线如图4所示。 图4 17CrNiMo6材料的应变-寿命曲线Fig.4 Strain-life curve of 17CrNiMo6 material 对齿轮进行脉动疲劳试验时,试验齿轮处于静止状态,压在轮齿上的压头作脉动循环加载,从而使轮齿产生疲劳折断。 试验时计算齿根应力,为了保证试验结果的可靠性,用有限元精确计算齿根应力。 定义齿轮单元类型为六面体单元,定义材料的杨氏模量为2.06×105MPa,泊松比为0.3。划分网格时再受载及受载附近的两个齿的齿根及齿廓等各面进行细化,采用扫略划分。加载时,由于试验条件下,受载齿轮齿廓与压头开始时是线接触,载荷增加时,会变成微小面接触,因此在ANSYS中选择受载节点时,选取加载点所在直线附近微小面积内的所有节点,受载力为总载荷除以受载点个数,以ME质量要求的齿轮为例子如图5所示,附齿轮加载图。加载力是垂直于加载点所在齿廓的切线方向[6-7]。完成上述设定之后,进行求解,并将其中一个计算结果以图6形式给出。 将有限元计算出的最大齿根弯曲应力,整理为表格形式。表6是不同齿高系数齿轮在5种应力级别下的结果。 表6 ANSYS分析齿轮齿高系数——最大齿根弯曲应力Table 6 ANSYS analysis of gear tooth height coefficient-maximum tooth root bending stress 不同齿高系数齿轮齿根应力载荷级别 12345 1652.806568.399522.07489.19465.234 1.15685.924597.265547.935514.555488.849 1.25721.278628.055576.286546.129514.035 以表6数据为基础,用局部应力应变分析方法计算试验齿轮疲劳寿命,结果如表7所示。 表7 轮齿失效寿命预测值Table 7 Predicted values of gear tooth failure life 在标准齿轮弯曲疲劳试验台上,制定非标准齿轮试验方案,确定的应力级别再用局部应力应变计算齿轮疲劳寿命的模型,分析齿高系数与齿轮弯曲疲劳寿命的关系,从结果分析可以看出,齿高系数改变了齿轮的齿根应力,从而也影响着齿轮的弯曲疲劳寿命,齿高系数越大,齿根弯曲疲劳寿命越短,齿轮的弯曲承载能力越低。


2 齿轮疲劳寿命预测

2.1 齿轮材料特性

2.2 循环应力-应变曲线





2.3 应变-寿命曲线


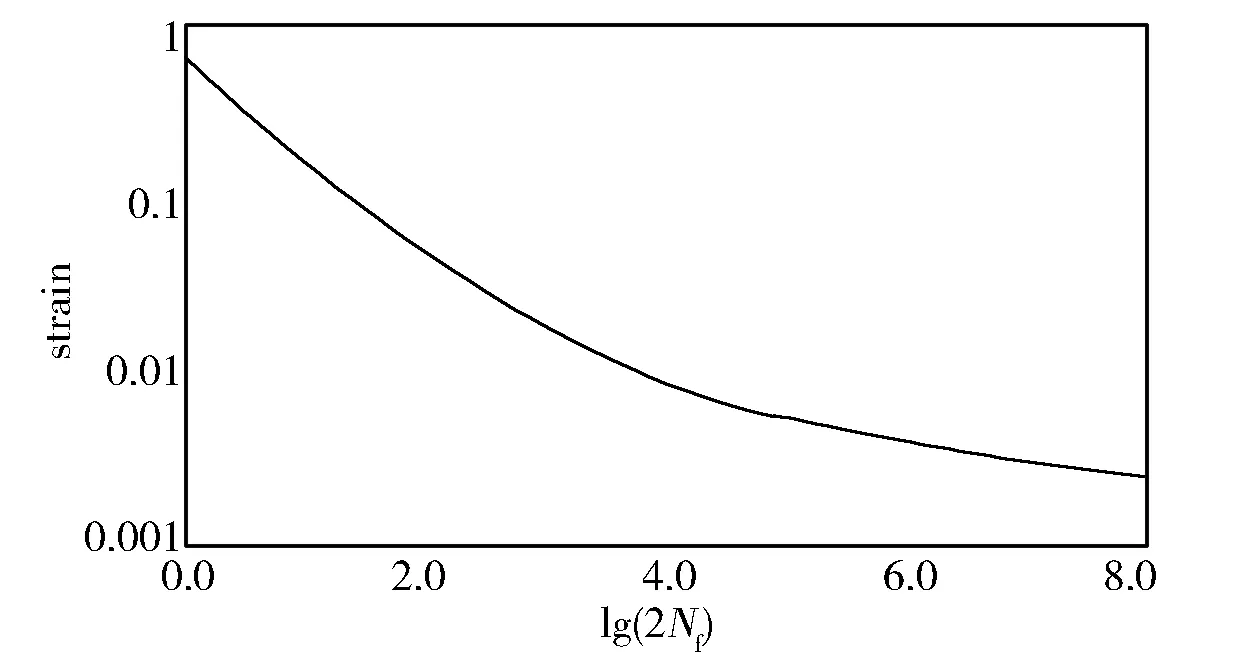
2.4 预测试验齿轮疲劳寿命



3 结语
