激光散斑法测量横向微位移及其应用

张 莉，杨伊凡，荣振宇，曲祥文，蒋伊麦

(济南大学 物理科学与技术学院，山东 济南 250022)

在物理实验中，微位移是比较常见的待测物理量，例如在拉伸法测杨氏模量、线膨胀系数测量等实验中均是通过测量微位移来实现杨氏模量或者线膨胀系数的间接测量. 在这类实验中，除了传统的千分表法[1]和光杠杆法[2]之外，还可以采用电学、磁学传感器[3]或者光学干涉法[4-5]进行测量，而传感器与计算机相结合则可以实现智能测量[6-7]. 其中，散斑照相术测微位移是光学干涉计量的一个分支. 在以往的利用散斑照相术测量微位移过程中，往往针对二次曝光散斑图像的功率谱的干涉条纹周期进行测量[8-9]，但这一测量会受到条纹对比度低、噪声大的影响. 本文在此工作的基础上将功率谱再做1次傅里叶变换，即可得到3个自相关强度分布，其峰值点的间距与物体的横向微位移量有关. 在实验中仅需测量最终光场中相邻2个自相关强度峰值点的间距，即可计算出物体的横向位移量. 整个实验利用CCD记录散斑光场，并利用计算机进行数字化处理，实现了微位移的智能化、自动化测量.

1 实验原理

利用激光散斑测量横向微位移的实验光路图如图1所示. 1束扩束的激光照射一粗糙物体的表面xoy，成像透镜L将物体表面所形成的散斑成像在其像平面x′o′y′上，处于像平面上的图像传感器(例如CCD)将采集的散斑强度分布S1(x′,y′)保存为计算机图片.

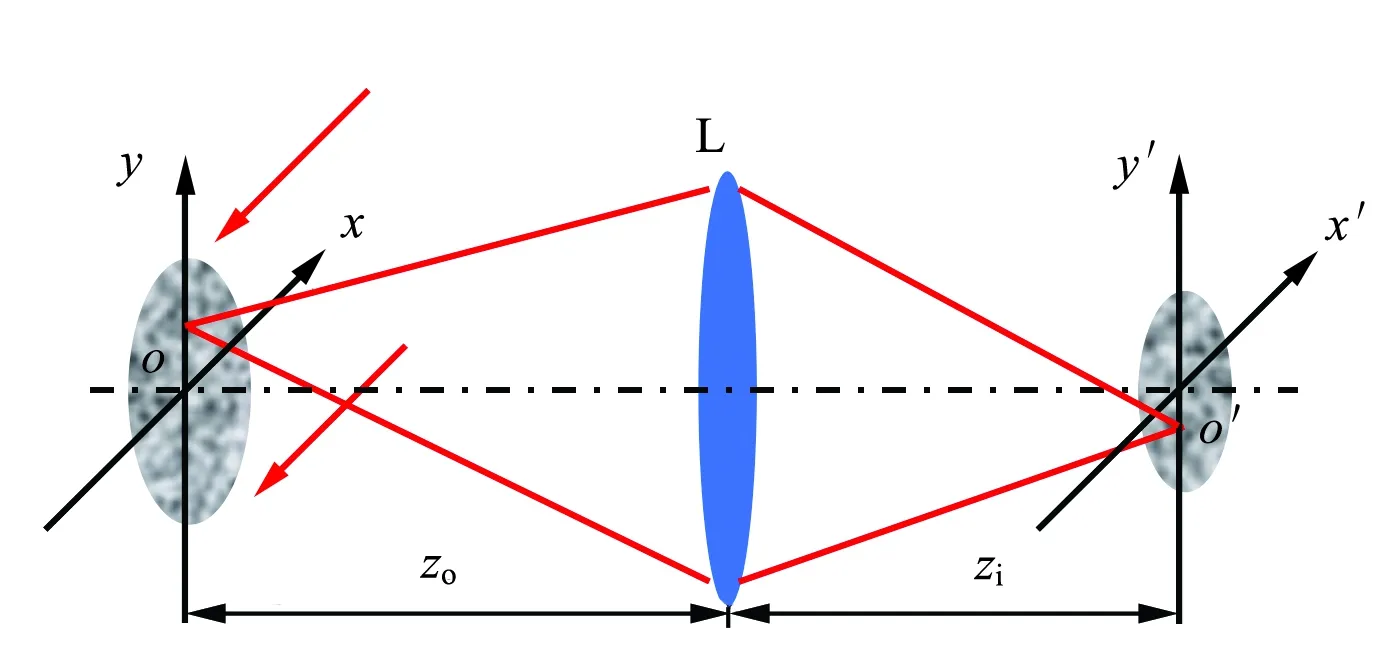
图1 散斑照相术的实验光路图

当物体沿x轴方向发生Δx的面内横向位移后，CCD在相同的曝光条件下记录下发生横向位移后的散斑强度分布S2(x′,y′). 由于散斑光场S2(x′,y′)相比较于S1(x′,y′)的强度分布是相同的，仅是产生了MΔx的横向位移，其中M=zi/zo是透镜成像的横向放大倍率，因此二者的强度分布关系为

S2(x′,y′)=S1(x′-MΔx,y′).

(1)

通过计算机可以将2幅散斑图像的强度相加，即可得到二次曝光的散斑强度分布为

S(x′,y′)=S1(x′,y′)*[δ(x′,y′)+

δ(x′-MΔx,y′)],

(2)

将二次曝光散斑强度分布做1次傅里叶变换，其频谱复振幅分布为

G(ξ,η)=F{S1(x′,y′)}·

[1+exp (-j2πMΔxξ)],

(3)

则该平面上所得到的光场强度分布，即功率谱的分布为

IG(ξ,η)=|F{S1(x′,y′)}|2·

2[1+cos (2πMΔxξ)],

(4)

该功率谱在频谱面上以空间坐标(xf,yf)为自变量的分布为

(5)

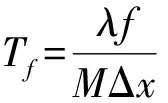
正是由于功率谱光场的条纹受到了未发生横向位移的散斑强度的功率谱的调制，从而导致该条纹对比度低、噪声大，这会给条纹周期的测量引入较大的误差. 如果将式(4)对应的功率谱再次进行逆傅里叶变换，则有

F-1{IG(ξ,η)}=[S1(x′,y′)⊗S1(x′,y′)]*

[2δ(x′,y′)+δ(x′-MΔx,y′)+

δ(x′+MΔx,y′)],

(6)

其光场强度分布为

|F-1{IG(ξ,η)}|2=|S1(x′,y′)⊗S1(x′,y′)|2*

[4δ(x′,y′)+δ(x′-MΔx,y′)+

δ(x′+MΔx,y′)],

(7)

式中⊗为相关运算符号，*为卷积运算符号. 由式(7)可以看出，在功率谱的逆傅里叶变换光场中，分别以(x′=0,y′ =0)，(x′=MΔx,y′ =0)，(x′=-MΔx,y′=0)3个点为中心分布着S1(x′,y′)的自相关强度光场. 由于自相关光场在其分布的中心有着极大的自相关峰，因此在功率谱的逆傅里叶变换光场中能够测量相邻2个自相关强度峰在x轴方向上的间距Δx，并根据关系式Δx=MΔx便可计算出物体在该方向上所发生的面内横向位移量Δx. 同理，在计算出物体沿y轴方向发生的面内横向位移量Δy后，即可计算物体在面内任意方向发生的横向位移量.

2 实验过程

根据上述激光散斑法测量横向微位移的原理分析，将该方法用于金属线膨胀系数测量. 在杭州大华公司研制的DH0505热膨胀实验仪的基础上，去掉原光路各光学元件，在金属棒的上端固定带有刻度的白板，激光器发出的激光经扩束后照射在白板上. 调整成像透镜与CCD的位置，使得CCD能够获得清晰的散斑像. 实验装置如图2所示. 利用白板上的刻度与CCD记录的刻度的像可以测量所搭建成像系统的横向放大倍率. 在实验开始前，使用CCD记录下白板在初始位置时的散斑分布[如图3(a)所示]；之后设置好加热的温度上限，开启加热键，在金属棒被加热过程中每隔3 ℃使用CCD记录1次散斑分布[加热到35 ℃时的散斑分布如图3(b)所示].

图2 实验装置图

在实验中记录下不同温度所对应的散斑强度分布，利用计算机分别将散斑分布图与初始的散斑分布图做等权重叠加，得到该温度相对于起始温度的二次曝光散斑分布[如图3(c)所示]. 再利用快速傅里叶变换算法对二次曝光的散斑强度图进行傅里叶变换，得到的功率谱分布取对数显示如图3(d)所示. 最后，再次利用快速傅里叶变换算法将功率谱做逆傅里叶变换，所得到的光场强度分布如图4所示. 图4中3个亮点对应3个初始散斑的自相关强度分布，沿光场中心2个正交方向的一维强度分布分别如图4中上方和左侧的曲线所示. 由一维强度分布曲线可以看出，通过计算机处理所得到的3个自相关强度分布的峰值非常尖锐，这为精确测量自相关强度峰值点的间距提供了便利条件.

(a) 室温下原始的散斑 (b) 加热到35 ℃的散 强度分布 斑强度分布

(c) 等权重叠加后的二次曝光 (d) 二次曝光散斑强度的 散斑强度分布 功率谱分布图3 CCD记录的散斑强度分布图

图4 功率谱的逆傅里叶变换光场强度分布

3 测量结果与分析

搭建图2所示的激光散斑测金属线膨胀系数的实验光路. 实验中采用He-Ne激光器，其波长λ=632.8 nm，成像镜头焦距f=300 mm，经测量所用成像系统的横向放大倍率M=0.972 8，待测金属棒在29 ℃下长度L0=150.10 mm，使用像素尺寸为2.4 μm×2.4 μm的CCD记录散斑光场. 实验中温度变化范围为29～60 ℃，每隔3 ℃记录1幅散斑分布图，共记录11幅散斑分布图. 通过计算机对所采集图像进行处理，并测量最终光场中相邻两自相关强度峰值点的间距Δ，以及计算该温度下散斑的横向微位移量(即金属棒在该温度下的伸长量)ΔL如表1所示. 将计算所得金属棒的伸长量ΔLm及相应温度Tm进行线性拟合(拟合曲线如图5所示)，所得拟合斜率k=(0.003 67±0.000 05) mm/℃ (P=95.5%)，拟合相关度γ=0.999 8. 将拟合的斜率代入金属棒线膨胀系数的定义式：

(8)

即可计算出所测金属棒的线膨胀系数α=(2.45±0.04)×10-5/℃(P=95.5%).

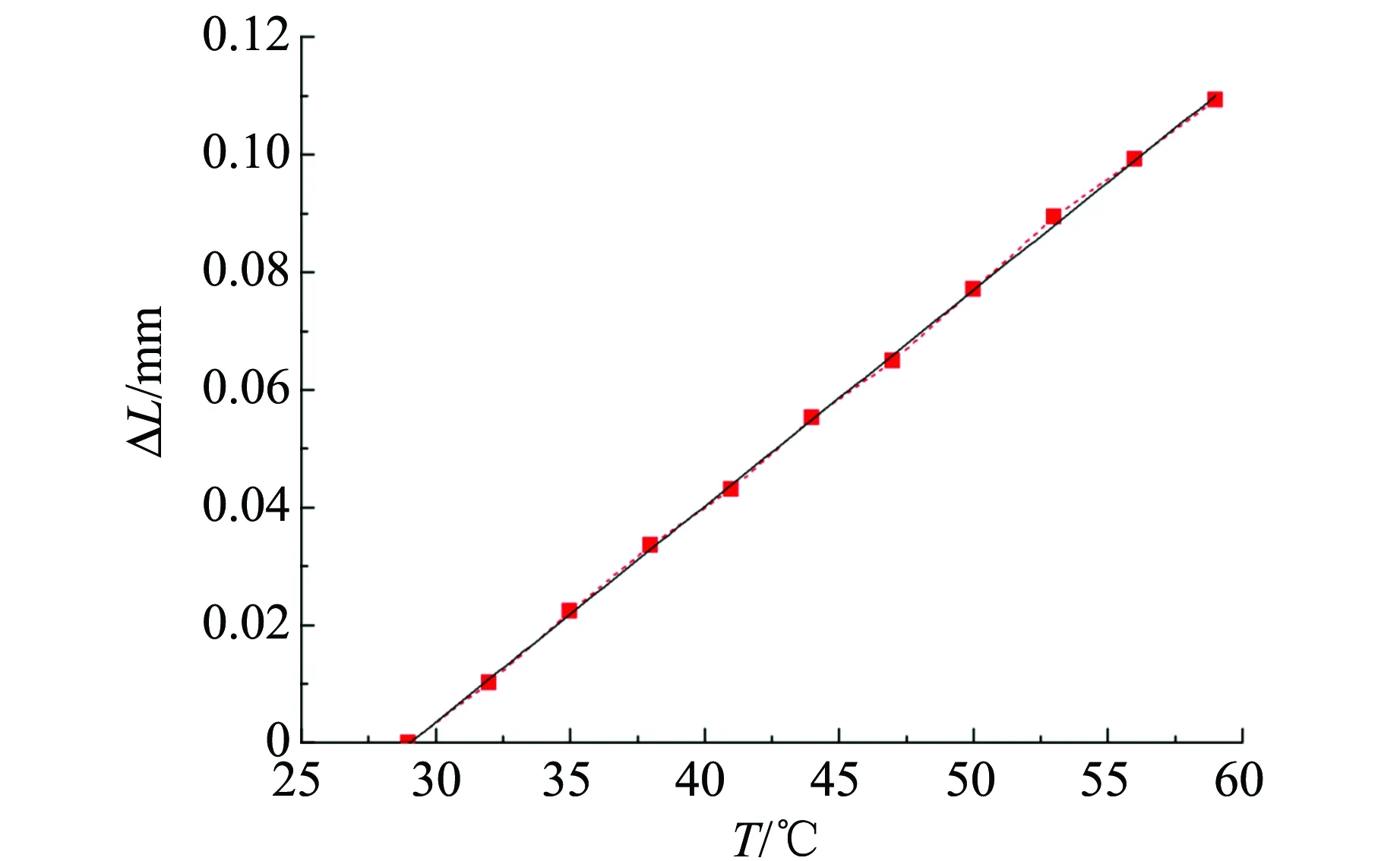
图5 金属棒的伸长量ΔL及相应温度T的线性拟合

表1 实验数据

4 结 论

通过测量结果可以看出，借助二次曝光散斑功率谱的逆傅里叶变换光场的自相关强度峰值点的间距来测量金属棒的微小伸长量，可以有效避免以往实验方法中条纹对比度低、噪声大所带来的影响，实验结果具有较好的线性关系. 利用激光散斑法测量横向微位移量，具有光路结构简单，实验操作简便，实现非接触式测量的优点. 该方法还可以应用于其他横向微位移量的测量，具有很好的应用前景.